CHAPTER 13 Graphs Java Software Structures Designing and

CHAPTER 13: Graphs Java Software Structures: Designing and Using Data Structures Third Edition John Lewis & Joseph Chase Addison Wesley is an imprint of © 2010 Pearson Addison-Wesley. All rights reserved.

Chapter Objectives • • Define undirected graphs Define weighted graphs or networks Explore common graph algorithms 1 -2 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -2

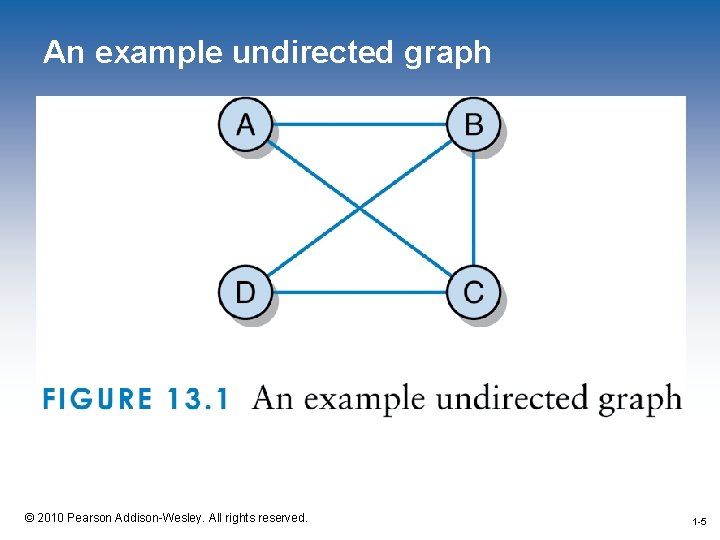
Graphs • Like a tree, a graph is made up of nodes and the connections between those nodes • In graph terminology, we refer to the nodes a vertices and the connections as edges • Vertices are typically referred to by label (e. g. A, B, C, D) • Edges are referenced by a paring of vertices (e. g. (A, B) represent an edge between A and B) 1 -3 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -3

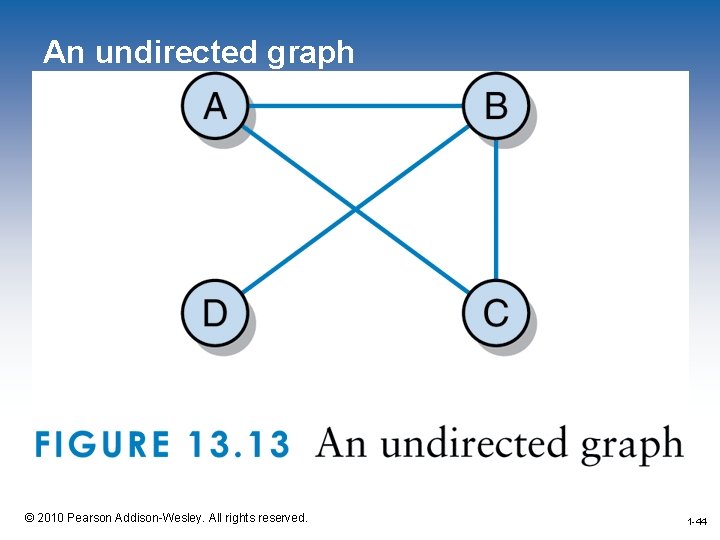
Undirected Graphs • An undirected graph is a graph where the pairings representing edges are unordered • Listing an edge as (A, B) means that there is an edge between A and B that can traversed in either direction • For an undirected graph, (A, B) means exactly the same thing as (B, A) 1 -4 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -4

An example undirected graph 1 -5 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -5

Undirected Graphs • Two vertices in a graph are adjacent if there is an edge connecting them • Adjacent vertices are sometimes referred to as neighbors • An edge of a graph that connects a vertex to itself is called a self-loop or a sling • An undirected graph is considered complete if it has the maximum number of edges connecting vertices (n(n-1)/2) 1 -6 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -6

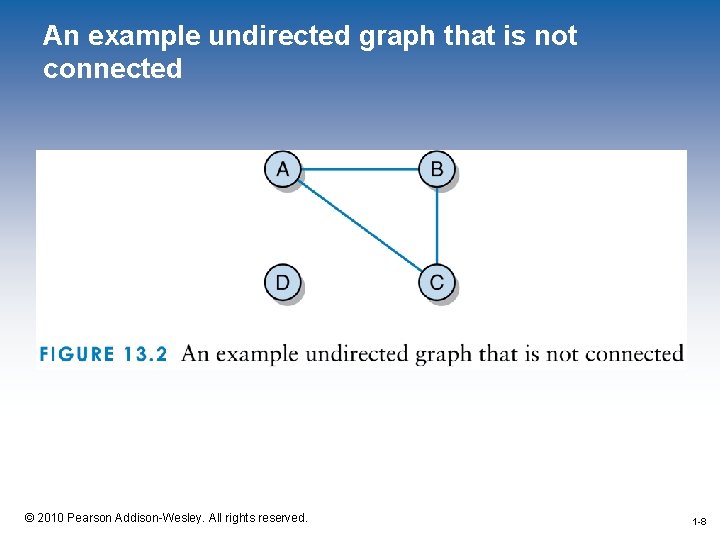
Undirected Graphs • A path is a sequence of edges that connects two vertices in a graph – A, B, D is a path from A to D in our previous example • The length of a path is the number of edges in the path (number of vertices - 1) • An undirected graph is considered connected if for any two vertices in the graph, there is a path between them – The graph in our previous example is connected – The following graph is not connected 1 -7 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -7

An example undirected graph that is not connected 1 -8 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -8

Undirected Graphs • A cycle is a path in which the first and last vertices are repeated – For example, in the previous slide, A, B, C, A is a cycle • A graph that has no cycles is called acyclic • An undirected tree is a connected, acyclic, undirected graph with one element designated as the root 1 -9 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -9

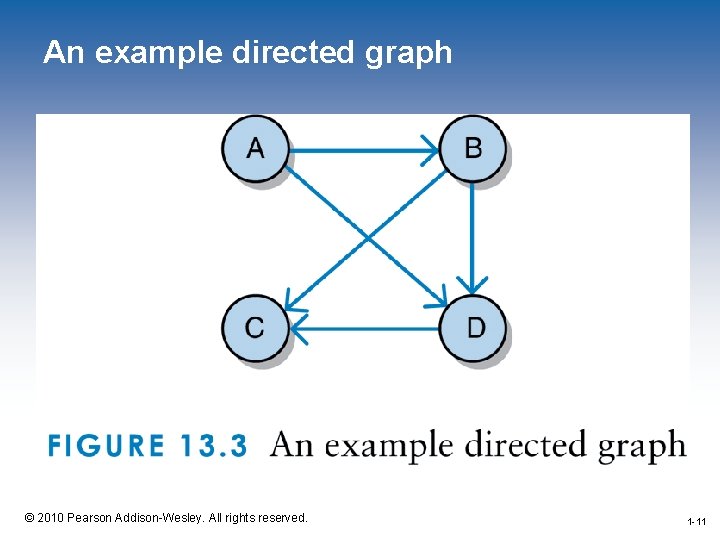
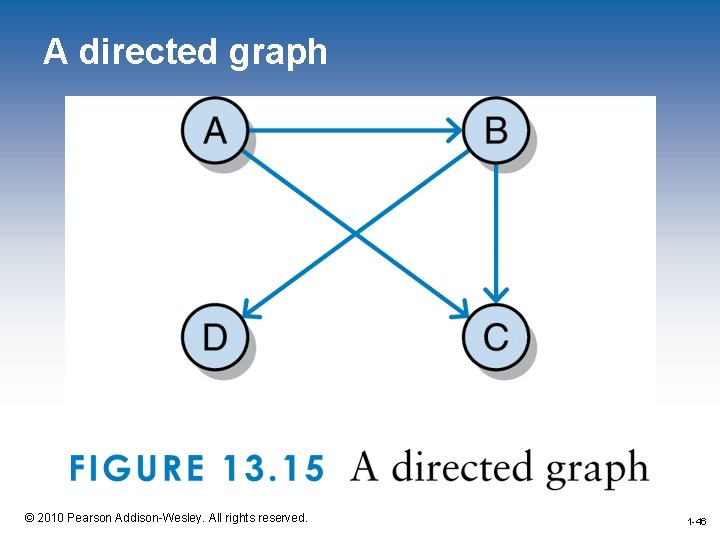
Directed Graphs • A directed graph, or digraph, is a graph where the edges are ordered pairs of vertices • This means that the edge (A, B) and (B, A) are separate, directional edges • Figure 13. 1 was described as: Vertices: Edges: A, B, C, D (A, B), (A, C), (B, D), (C, D) • Interpreting this as a directed graph yields the graph in Figure 13. 3 1 -10 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -10

An example directed graph 1 -11 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -11

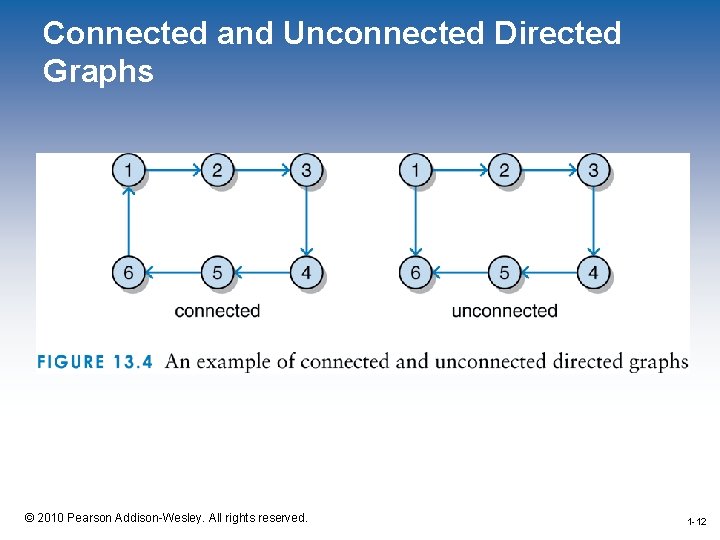
Connected and Unconnected Directed Graphs 1 -12 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -12

Directed Graphs • If a directed graph has no cycles, it is possible to arrange the vertices such that vertex A precedes vertex B if an edge exists from A to B • This order of vertices is called topological order • A directed tree is a directed graph that has an element designated as the root and has the following properties – There are no connections from other vertices to the root – Every non-root element has exactly on connection to it – There is a path from the root to every other vertex 1 -13 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -13

Networks • A network or a weighted graph is a graph with weights or costs associated with each edge • Figure 13. 5 shows an undirected network of the connections and airfares between cities • Networks may be directed or undirected • Figure 13. 6 shows a directed network 1 -14 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -14

A network, or weighted graph 1 -15 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -15

A directed network 1 -16 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -16

Networks • For networks, we represent each edge with a triple including the starting vertex, the ending vertex, and the weight (Boston, New York, 120) 1 -17 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -17

Common Graph Algorithms • For trees, we defined four types of traversals • Generally, we divide graph traversals into two categories – Breadth-first traversal – Depth-first traversal 1 -18 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -18

Common Graph Algorithms • We can construct a breadth-first traversal for a graph similarly to our level-order traversal of a tree – Use a queue and an unordered list – We use the queue to manage the traversal – We use the unordered list to build our result 1 -19 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -19

A Breadth First Iterator /** * Returns an iterator that performs a breadth first search * traversal starting at the given index. * * @param start. Index the index to begin the search from * @return an iterator that performs a breadth first traversal */ public Iterator<T> iterator. BFS(int start. Index) { Integer x; Linked. Queue<Integer> traversal. Queue = new Linked. Queue<Integer>(); Array. Unordered. List<T> result. List = new Array. Unordered. List<T>(); if (!index. Is. Valid(start. Index)) return result. List. iterator(); boolean[] visited = new boolean[num. Vertices]; for (int i = 0; i < num. Vertices; i++) visited[i] = false; traversal. Queue. enqueue(new Integer(start. Index)); visited[start. Index] = true; 1 -20 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -20

A Breadth First Iterator (continued) while (!traversal. Queue. is. Empty()) { x = traversal. Queue. dequeue(); result. List. add. To. Rear(vertices[x. int. Value()]); /** Find all vertices adjacent to x that have not been visited and queue them up */ for (int i = 0; i < num. Vertices; i++) { if (adj. Matrix[x. int. Value()][i] && !visited[i]) { traversal. Queue. enqueue(new Integer(i)); visited[i] = true; } } } return result. List. iterator(); } 1 -21 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -21

Common Graph Algorithms • We can construct a depth-first traversal for a graph similarly to our level-order traversal of a tree by replacing the queue with a stack – Use a stack and an unordered list – We use the stack to manage the traversal – We use the unordered list to build our result 1 -22 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -22

A Depth First Iterator /** * Returns an iterator that performs a depth first search * traversal starting at the given index. * * @param start. Index the index to begin the search traversal from * @return an iterator that performs a depth first traversal */ public Iterator<T> iterator. DFS(int start. Index) { Integer x; boolean found; Linked. Stack<Integer> traversal. Stack = new Linked. Stack<Integer>(); Array. Unordered. List<T> result. List = new Array. Unordered. List<T>(); boolean[] visited = new boolean[num. Vertices]; if (!index. Is. Valid(start. Index)) return result. List. iterator(); for (int i = 0; i < num. Vertices; i++) visited[i] = false; traversal. Stack. push(new Integer(start. Index)); result. List. add. To. Rear(vertices[start. Index]); visited[start. Index] = true; © 2010 Pearson Addison-Wesley. All rights reserved. 1 -23

A Depth First Iterator (continued) while (!traversal. Stack. is. Empty()) { x = traversal. Stack. peek(); found = false; /** Find a vertex adjacent to x that has not been visited and push it on the stack */ for (int i = 0; (i < num. Vertices) && !found; i++) { if (adj. Matrix[x. int. Value()][i] && !visited[i]) { traversal. Stack. push(new Integer(i)); result. List. add. To. Rear(vertices[i]); visited[i] = true; found = true; } } if (!found && !traversal. Stack. is. Empty()) traversal. Stack. pop(); } return result. List. iterator(); } 1 -24 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -24

Common Graph Algorithms • Of course, both of these algorithms could be expressed recursively 1 -25 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -25

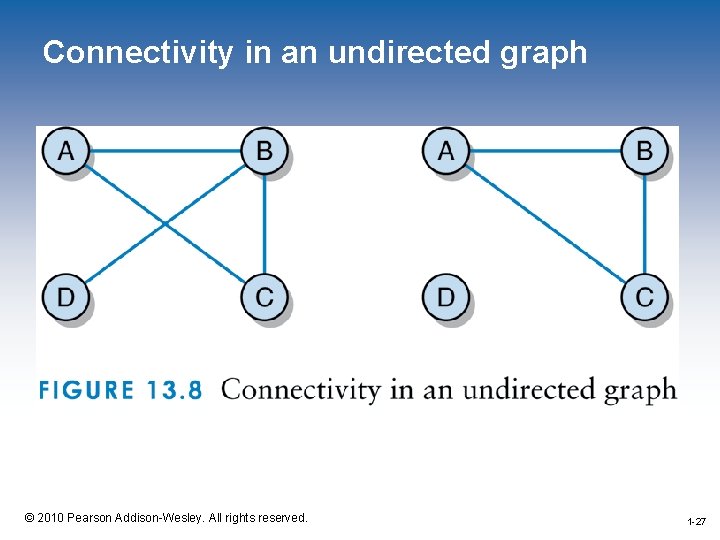
Common Graph Algorithms • Another common graph algorithm is testing for connectivity • The graph is connected if and only if for each vertex v in a graph containing n vertices, the size of the result of a breadthfirst traversal starting a v is n 1 -26 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -26

Connectivity in an undirected graph 1 -27 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -27

Breadth-first traversals for a connected undirected graph 1 -28 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -28

Breadth-first traversals for an unconnected undirected graph 1 -29 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -29

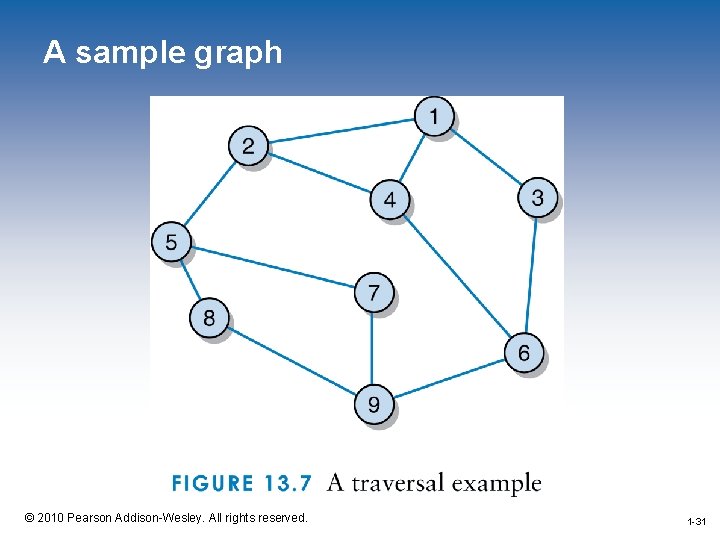
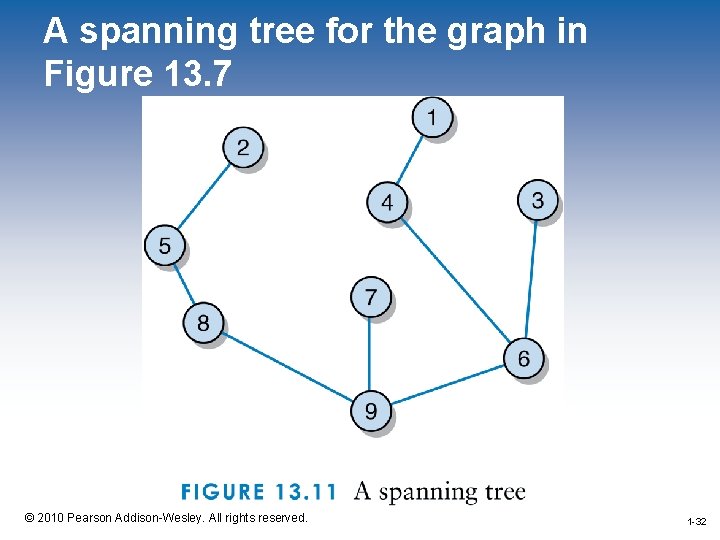
Spanning Trees • A spanning tree is a tree that includes all of the vertices of a graph • The following example shows a graph and then a spanning tree for that graph 1 -30 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -30

A sample graph 1 -31 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -31

A spanning tree for the graph in Figure 13. 7 1 -32 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -32

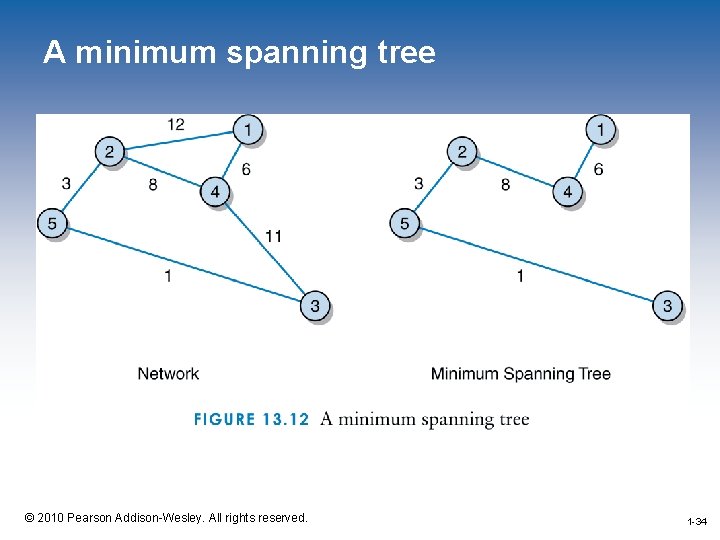
Minimum Spanning Trees • A minimum spanning tree is a spanning tree where the sum of the weights of the edges is less than or equal to the sum of the weights for any other spanning tree for the same graph • The algorithm for creating a minimum spanning tree makes use of a minheap to order the edges 1 -33 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -33

A minimum spanning tree 1 -34 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -34

A Minimum Spanning Tree /** * Returns a minimum spanning tree of the network. * * @return a minimum spanning tree of the network */ public Network mst. Network() { int x, y; int index; double weight; int[] edge = new int[2]; Heap<Double> min. Heap = new Heap<Double>(); Network<T> result. Graph = new Network<T>(); if (is. Empty() || !is. Connected()) return result. Graph; result. Graph. adj. Matrix = new double[num. Vertices]; for (int i = 0; i < num. Vertices; i++) for (int j = 0; j < num. Vertices; j++) result. Graph. adj. Matrix[i][j] = Double. POSITIVE_INFINITY; result. Graph. vertices = (T[])(new Object[num. Vertices]); 1 -35 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -35

A Minimum Spanning Tree boolean[] visited = new boolean[num. Vertices]; for (int i = 0; i < num. Vertices; i++) visited[i] = false; edge[0] = 0; result. Graph. vertices[0] = this. vertices[0]; result. Graph. num. Vertices++; visited[0] = true; /** Add all edges, which are adjacent to the starting vertex, to the heap */ for (int i = 0; i < num. Vertices; i++) min. Heap. add. Element(new Double(adj. Matrix[0][i])); while ((result. Graph. size() < this. size()) && !min. Heap. is. Empty()) { /** Get the edge with the smallest weight that has exactly one vertex already in the result. Graph */ do { weight = (min. Heap. remove. Min()). double. Value(); edge = get. Edge. With. Weight. Of(weight, visited); } while (!index. Is. Valid(edge[0]) || !index. Is. Valid(edge[1])); © 2010 Pearson Addison-Wesley. All rights reserved. 1 -36

A Minimum Spanning Tree x = edge[0]; y = edge[1]; if (!visited[x]) index = x; else index = y; /** Add the new edge and vertex to the result. Graph */ result. Graph. vertices[index] = this. vertices[index]; visited[index] = true; result. Graph. num. Vertices++; result. Graph. adj. Matrix[x][y] = this. adj. Matrix[x][y]; result. Graph. adj. Matrix[y][x] = this. adj. Matrix[y][x]; 1 -37 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -37

A Minimum Spanning Tree /** Add all edges, that are adjacent to the newly added vertex, to the heap */ for (int i = 0; i < num. Vertices; i++) { if (!visited[i] && (this. adj. Matrix[i][index] < Double. POSITIVE_INFINITY)) { edge[0] = index; edge[1] = I; min. Heap. add. Element(new Double(adj. Matrix[index][i])); } } } return result. Graph; } 1 -38 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -38

Determining the Shortest Path • There are two possibilities for determining the shortest path in a graph – Determine the literal shortest path in terms of the number of edges – Determine the least expensive path in a network 1 -39 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -39

Determining the Shortest Path • The solution to the first of these is a simple variation of our earlier breadth-first traversal algorithm • We simply store two additional pieces of information for each vertex – The path length from the starting point to this vertex – The vertex that is the predecessor of this vertex on that path • Then we modify our loop to terminate when we reach our target vertex 1 -40 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -40

Determining the Shortest Path • The second possibility is to look for the cheapest path in a network • Dijkstra develop an algorithm for this possibility that is similar to our previous algorithm • However, instead of using a queue of vertices, we use a minheap or a priority queue storing vertex, weight pairs based upon total weight • Thus we always traverse through the graph following the cheapest path first 1 -41 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -41

Strategies for Implementing Graphs • There are two principle approaches to implementing graphs – Adjacency lists – Adjacency matrices • The adjacency list approach is modeled closely to the way we implemented linked implementations of trees • However, instead of building a graph node that contains a fixed number of references (as we did with Binary. Tree. Node) we will build a graph node that simply maintain a linked lists of references to other nodes • This list is called an adjacency list 1 -42 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -42

Strategies for Implementing Graphs • The second strategy for implementing graphs is to use an adjacency matrix • An adjacency matrix is simply a two-dimensional array where both dimensions are “indexed” by the vertices of the graph • Each position in the matrix contains a boolean that is true if the two associated vertices are connected by an edge, and false otherwise • The following slides show two example of adjacency matrices, one for an undirected graph, the other for a directed graph • An adjacency matrix for a network could store the weights in each cell instead of a boolean 1 -43 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -43

An undirected graph 1 -44 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -44

An adjacency matrix for an undirected graph 1 -45 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -45

A directed graph 1 -46 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -46

An adjacency matrix for a directed graph 1 -47 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -47

A Graph. ADT /** * Graph. ADT defines the interface to a graph data structure. * * @author Dr. Chase * @author Dr. Lewis * @version 1. 0, 9/17/2008 */ package jss 2; import java. util. Iterator; public interface Graph. ADT<T> { /** * Adds a vertex to this graph, associating object with vertex. * * @param vertex the vertex to be added to this graph */ public void add. Vertex (T vertex); 1 -48 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -48

A Graph. ADT (continued) /** * Removes a single vertex with the given value from this graph. * * @param vertex the vertex to be removed from this graph */ public void remove. Vertex (T vertex); /** * Inserts an edge between two vertices of this graph. * * @param vertex 1 the first vertex * @param vertex 2 the second vertex */ public void add. Edge (T vertex 1, T vertex 2); /** * Removes an edge between two vertices of this graph. * * @param vertex 1 the first vertex * @param vertex 2 the second vertex */ public void remove. Edge (T vertex 1, T vertex 2); 1 -49 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -49

A Graph. ADT (continued) /** * Returns a breadth first iterator starting with the given vertex. * * @param start. Vertex the starting vertex * @return a breadth first iterator beginning at the given * vertex */ public Iterator iterator. BFS(T start. Vertex); /** * Returns a depth first iterator starting with the given vertex. * * @param start. Vertex the starting vertex * @return a depth first iterator starting at the given vertex */ public Iterator iterator. DFS(T start. Vertex); 1 -50 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -50

A Graph. ADT (continued) /** * Returns an iterator that contains the shortest path between * the two vertices. * * @param start. Vertex the starting vertex * @param target. Vertex the ending vertex * @return an iterator that contains the shortest path * between the two vertices */ public Iterator iterator. Shortest. Path(T start. Vertex, T target. Vertex); /** * Returns true if this graph is empty, false otherwise. * * @return true if this graph is empty */ public boolean is. Empty(); /** * Returns true if this graph is connected, false otherwise. * * @return true if this graph is connected */ public boolean is. Connected(); © 2010 Pearson Addison-Wesley. All rights reserved. 1 -51

A Graph. ADT (continued) /** * Returns the number of vertices in this graph. * * @return the integer number of vertices in this graph */ public int size(); /** * Returns a string representation of the adjacency matrix. * * @return a string representation of the adjacency matrix */ public String to. String(); } 1 -52 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -52

A Network. ADT /** * Network. ADT defines the interface to a network. * * @author Dr. Lewis * @author Dr. Chase * @version 1. 0, 9/17/2008 */ package jss 2; import java. util. Iterator; public interface Network. ADT<T> extends Graph. ADT<T> { /** * Inserts an edge between two vertices of this graph. * * @param vertex 1 the first vertex * @param vertex 2 the second vertex * @param weight the weight */ public void add. Edge (T vertex 1, T vertex 2, double weight); 1 -53 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -53

A Network. ADT (continued) /** * Returns the weight of the shortest path in this network. * * @param vertex 1 the first vertex * @param vertex 2 the second vertex * @return the weight of the shortest path in this network */ public double shortest. Path. Weight(T vertex 1, T vertex 2); } 1 -54 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -54

The Graph class /** * Graph represents an adjacency matrix implementation of a graph. * * @author Dr. Lewis * @author Dr. Chase * @version 1. 0, 9/16/2008 */ package jss 2; import jss 2. exceptions. *; import java. util. *; public class Graph<T> implements Graph. ADT<T> { protected final int DEFAULT_CAPACITY = 10; protected int num. Vertices; // number of vertices in the graph protected boolean[][] adj. Matrix; // adjacency matrix protected T[] vertices; // values of vertices 1 -55 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -55

The Graph class (continued) /** * Creates an empty graph. */ public Graph() { num. Vertices = 0; this. adj. Matrix = new boolean[DEFAULT_CAPACITY]; this. vertices = (T[])(new Object[DEFAULT_CAPACITY]); } 1 -56 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -56

Graph - add. Edge /** * Inserts an edge between two vertices of the graph. * * @param vertex 1 the first vertex * @param vertex 2 the second vertex */ public void add. Edge (T vertex 1, T vertex 2) { add. Edge (get. Index(vertex 1), get. Index(vertex 2)); } /** * Inserts an edge between two vertices of the graph. * * @param index 1 the first index * @param index 2 the second index */ public void add. Edge (int index 1, int index 2) { if (index. Is. Valid(index 1) && index. Is. Valid(index 2)) { adj. Matrix[index 1][index 2] = true; adj. Matrix[index 2][index 1] = true; } } © 2010 Pearson Addison-Wesley. All rights reserved. 1 -57

Graph - add. Vertex /** * Adds a vertex to the graph, expanding the capacity of the graph * if necessary. It also associates an object with the vertex. * * @param vertex the vertex to add to the graph */ public void add. Vertex (T vertex) { if (num. Vertices == vertices. length) expand. Capacity(); vertices[num. Vertices] = vertex; for (int i = 0; i <= num. Vertices; i++) { adj. Matrix[num. Vertices][i] = false; adj. Matrix[i][num. Vertices] = false; } num. Vertices++; } 1 -58 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -58