CHAPTER 13 FORCE AND ACCELARATION OBJECTIVES 1 To

CHAPTER 13 FORCE AND ACCELARATION

OBJECTIVES 1. To introduce the concepts of position, displacement, velocity and acceleration. 2. To study particle motion along a straight line (rectilinear motion) and represent this motion graphically.

CHAPTER OUTLINE 1. 2. 3. 4. Center of gravity. Centroid for area and lines. Composites bodies (plates and wires). Theorem of Pappus and Guldinus.

STATICS Newton’s first law SF=0 A particle originally at rest, will remain in rest. DYNAMICS Newton’s second law SF=ma A particle acted upon by an unbalanced force, experiences acceleration that has the same direction as the force and a magnitude that is directly proportional to the force.

FORCE and ACCELARATION RECTILINEAR MOTION CURVILINEAR MOTION

Rectilinear motion Curvilinear motion v = vo + act s = so + vot + act 2 v 2 = vo 2 + 2 ac(s-so) Constant acceleration Normal & Tangential Components

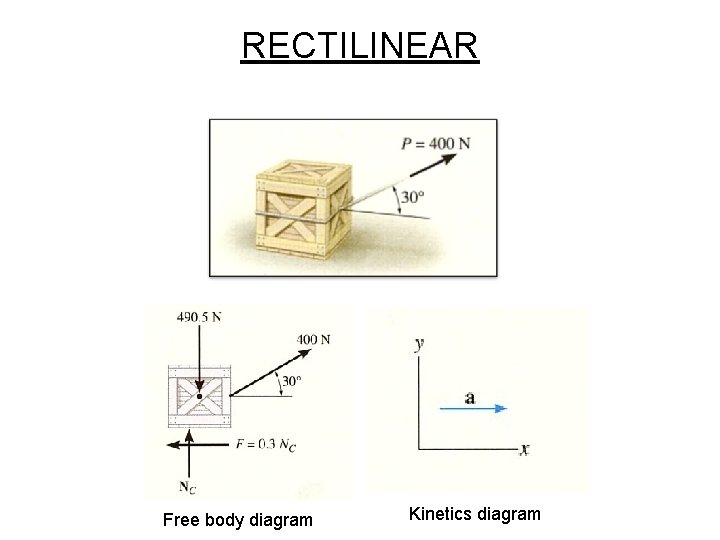
RECTILINEAR Free body diagram Kinetics diagram

Example 1 The crate has a mass of 50 kg. If the crate is subjected to a 400[N] towing force as shown, determine the velocity of the crate in 3[s] starting from rest. mk= 0. 3

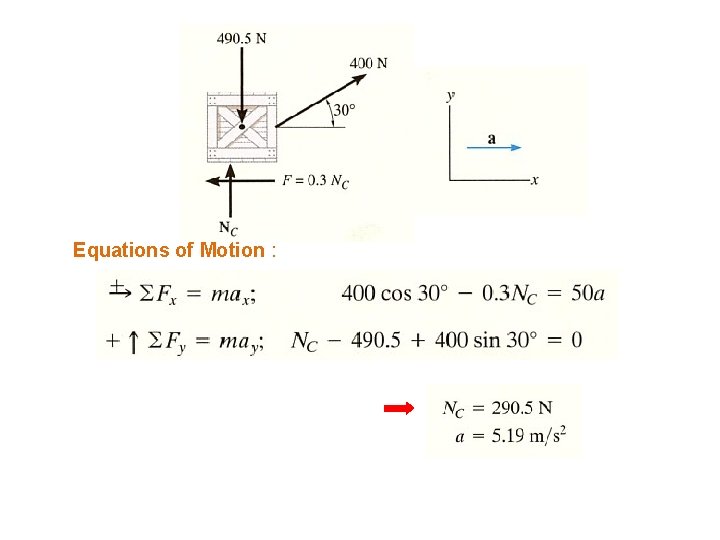
Equations of Motion :

Kinematics : The acceleration is constant, P is constant

Example 2 The crate has a mass of 80 kg. If the magnitude of P is increased until the crate begins to slide, determine the crate’s initial acceleration. ms= 0. 5, mk= 0. 2

80(9. 81) = 784. 8[N] P 20 o Given; ms= 0. 5 mk= 0. 2 : verge of slipping : impending motion Ff = 0. 5 N N Equations of equilibrium : SFx=0 ; SFy=0 ; Pcos 20 o – 0. 5 N = 0 N + Psin 20 o – 784. 8 = 0 P = 353. 29 N N = 663. 79 N ……. . (i) ……. . . (ii)

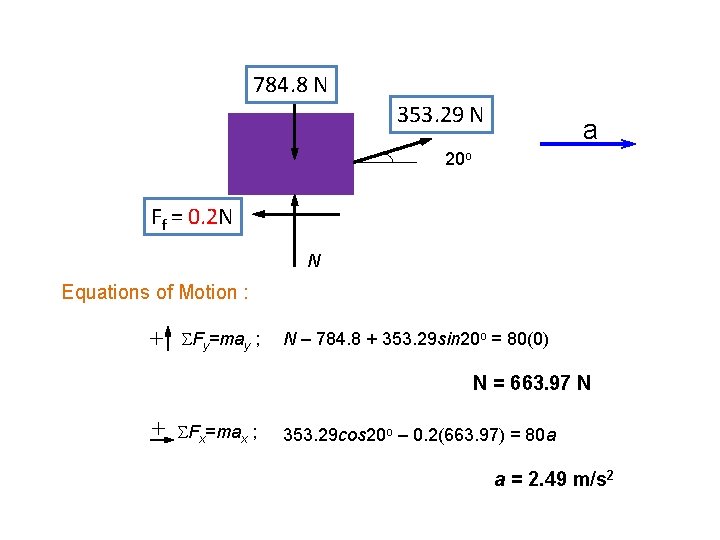
784. 8 N 353. 29 N a 20 o Ff = 0. 2 N N Equations of Motion : SFy=may ; N – 784. 8 + 353. 29 sin 20 o = 80(0) N = 663. 97 N SFx=max ; 353. 29 cos 20 o – 0. 2(663. 97) = 80 a a = 2. 49 m/s 2

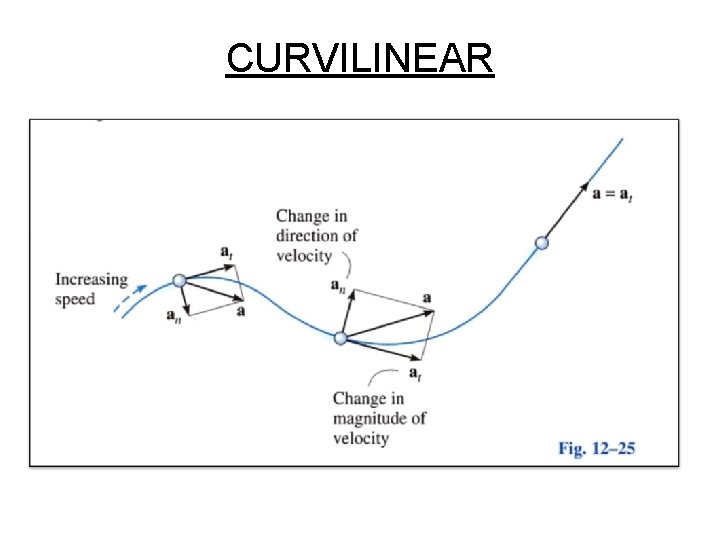
CURVILINEAR

o t When a particle moves along a curved path, it may be more convenient to write the equation of motion in terms of normal and tangential coordinates.

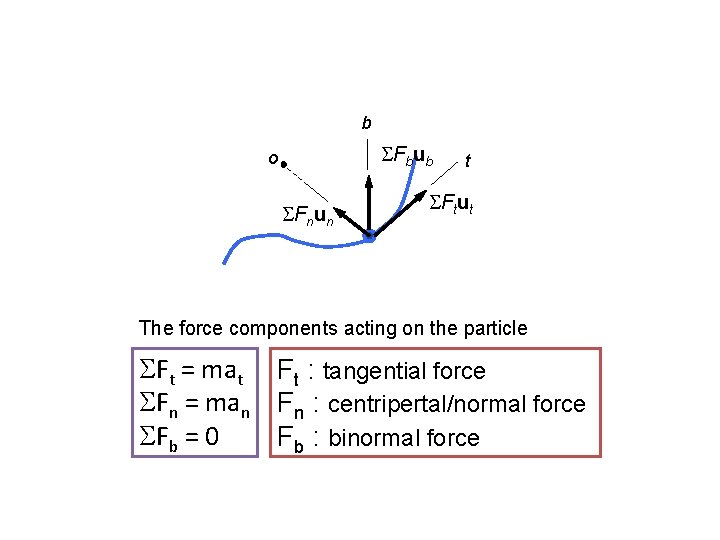
b SFbub o SFnun t SFtut The force components acting on the particle SFt = mat Ft : tangential force SFn = man Fn : centripertal/normal force SFb = 0 Fb : binormal force

Procedure for Analysis 1. 2. 3. 4. Draw FBD Draw kinetic diagram Apply equation of motion Consider kinematic related

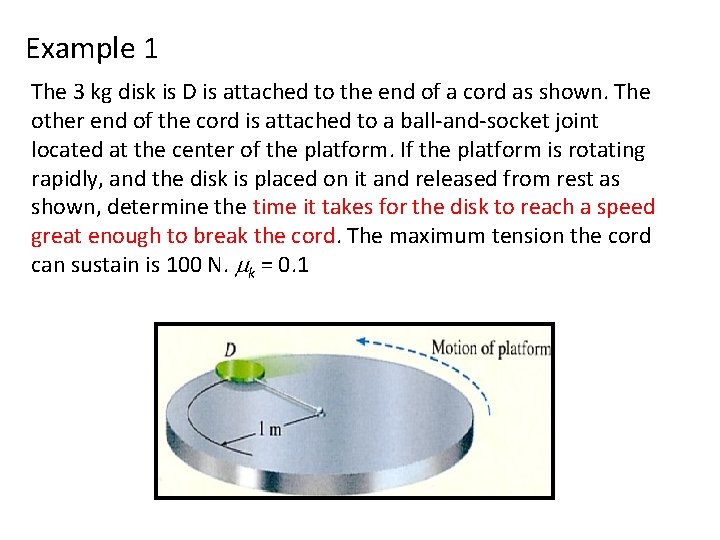
Example 1 The 3 kg disk is D is attached to the end of a cord as shown. The other end of the cord is attached to a ball-and-socket joint located at the center of the platform. If the platform is rotating rapidly, and the disk is placed on it and released from rest as shown, determine the time it takes for the disk to reach a speed great enough to break the cord. The maximum tension the cord can sustain is 100 N. mk = 0. 1

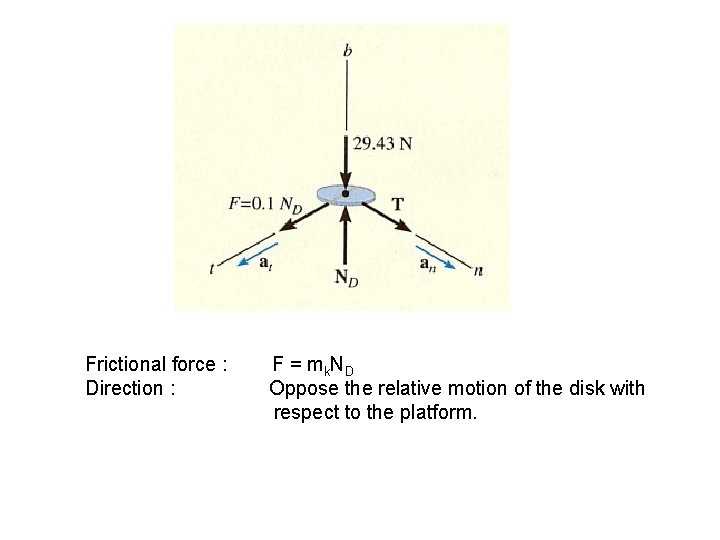
Frictional force : Direction : F = m k ND Oppose the relative motion of the disk with respect to the platform.

Equations of Motion : SFn=man ; SFt=mat ; SFb=0; T = m(v 2/r) = 3 v 2 0. 1 ND = 3 at ND – 29. 43 = 0 Setting T = 100 N to get critical speed Vcr Kinematics : Since at is constant, vcr = vo + att 5. 77 = 0 + (0. 981)t T = 5. 89 s Given; ND = 29. 43 N at = 0. 981 m/s 2 Vcr = 5. 77 m/s

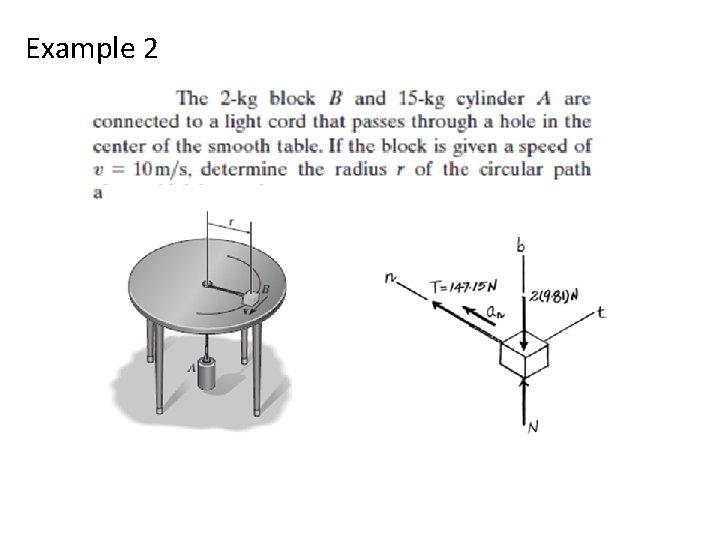
Example 2

Example 3