Chapter 12 The Structural Model in the Analysis

The Structural Model § Flexible way of figuring the two population variance estimates –

Principles of the Structural Model § Dividing up the deviations – Deviation of a

Principles of the Structural Model § From the sums of squared deviations to the

Principles of the Structural Model § Relation of the structural model approach to the

Using the Structural Model to Figure an ANOVA § Example analysis of variance table

Post-Hoc Comparisons § Exploratory approach § Scheffé test – Figure the F in the

Effect Size for ANOVA § Proportion of variance accounted for (R 2)

Effect Size for ANOVA § § R 2 also known as η 2 (eta

Power for ANOVA (. 05 significance level)

Approximate Sample Size Needed in Each Group for 80% Power (. 05 significance level)

Controversies and Limitations § Normal population distributions § Equal population variances § Independence –

Slides: 15

Download presentation

Chapter 12 The Structural Model in the Analysis of Variance

The Structural Model § Flexible way of figuring the two population variance estimates – Handles situation when sample sizes in each group are not equal – Insight into underlying logic of ANOVA

Principles of the Structural Model § Dividing up the deviations – Deviation of a score from the grand mean • Deviation of the score from the mean of its group • Deviation of the mean of its group from the grand mean § Summing the squared deviations

Principles of the Structural Model § From the sums of squared deviations to the population variance estimates

Principles of the Structural Model § Relation of the structural model approach to the Chapter 11 approach – Within-groups variance estimate • Never figure the variance estimate for each group and average them – Between-groups variance estimate • Never multiply anything by the number of scores in each sample – Same ingredients for the F ratio

Principles of the Structural Model § Relation of the structural model approach to the Chapter 11 approach – Chapter 11 • Emphasizes entire groups • Focuses directly on what contributes to the overall population variance estimates – Structural model • Emphasizes individual scores • Focuses directly on what contributes to the divisions of the deviations of scores from the grand mean

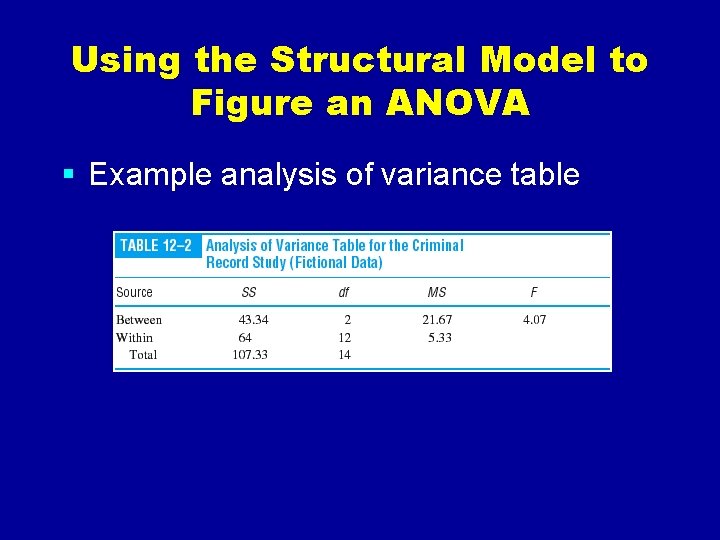
Using the Structural Model to Figure an ANOVA § Example analysis of variance table

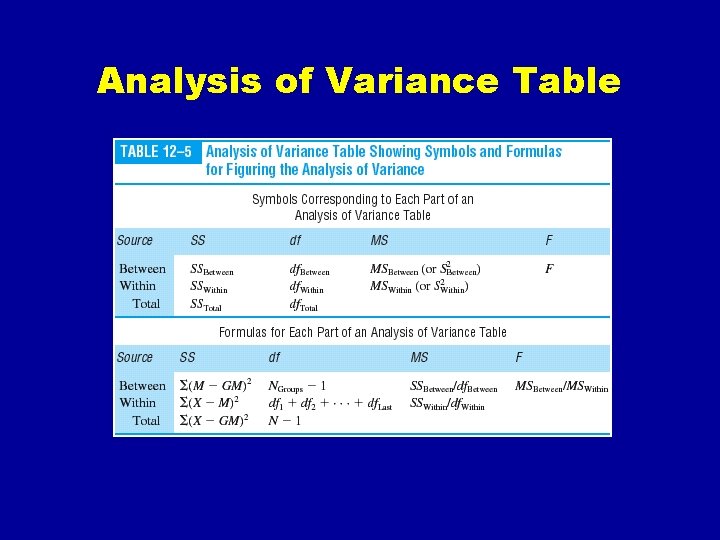
Analysis of Variance Table

Post-Hoc Comparisons § Exploratory approach § Scheffé test – Figure the F in the usual way – Divide the F by the overall study’s df. Between – Compare this to the overall study’s F cutoff

Effect Size for ANOVA § Proportion of variance accounted for (R 2)

Effect Size for ANOVA § § R 2 also known as η 2 (eta squared) small R 2 =. 01 medium R 2 =. 06 large R 2 =. 14

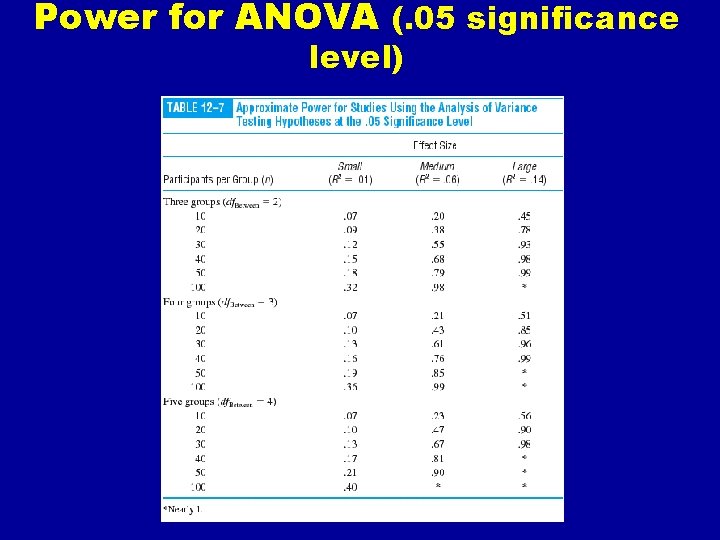
Power for ANOVA (. 05 significance level)

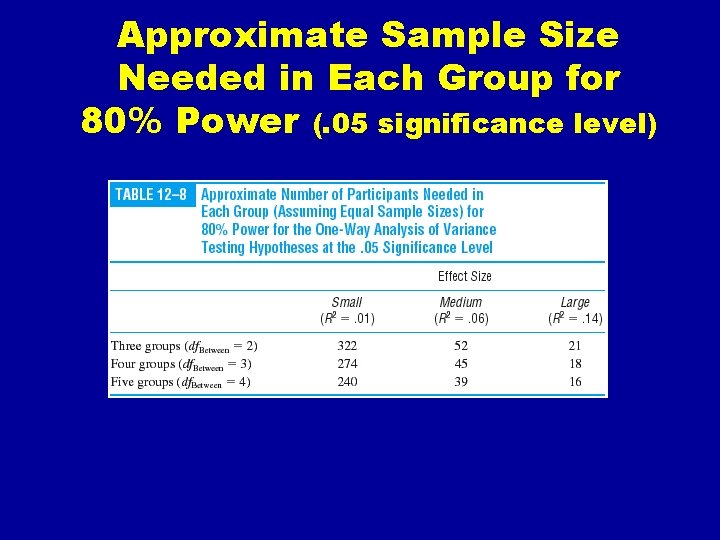
Approximate Sample Size Needed in Each Group for 80% Power (. 05 significance level)

Controversies and Limitations § Normal population distributions § Equal population variances § Independence – Each score is independent of the others – Unit of analysis

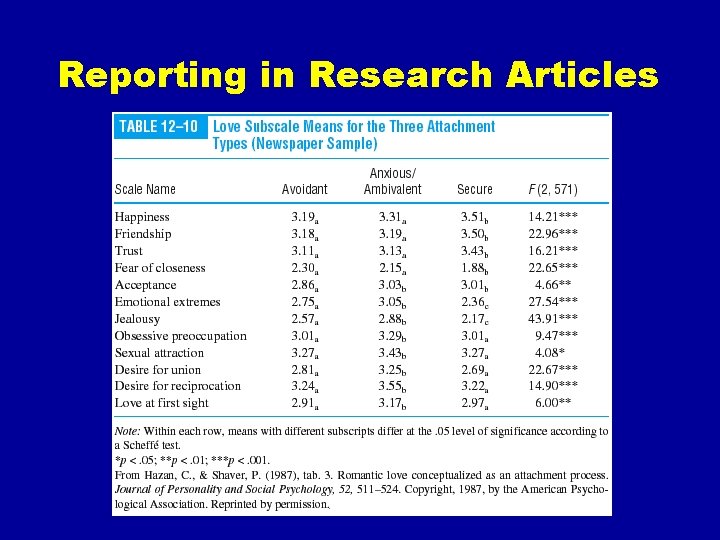
Reporting in Research Articles