Chapter 12 Stoichiometry Mr Mole Molar Mass of

Chapter 12 Stoichiometry Mr. Mole

Molar Mass of Compounds • Molar mass (MM) of a compound - determined by up the atomic masses 20 17 of Cl – Ex. Molar mass of Ca. Cl 2 – MM of Calcium = 40. 08 g/mol – MM of Chlorine = 35. 45 g g/mol – Molar Mass of Ca. Cl 2= 40. 08 g/mol Ca + 70. 9 g/mol Cl = Ca 40. 08 35. 45

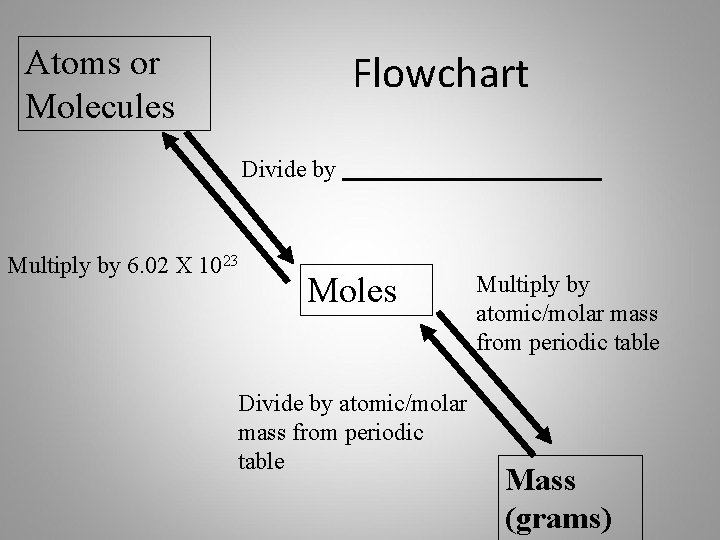
Atoms or Molecules Flowchart Divide by Multiply by 6. 02 X 1023 Moles Divide by atomic/molar mass from periodic table Multiply by atomic/molar mass from periodic table Mass (grams)

Practice • Calculate the Molar Mass of calcium phosphide – Formula = Ca 3 P 2 – Masses elements: Ca = 40. 08 g/mol P = 30. 97 g/mol –

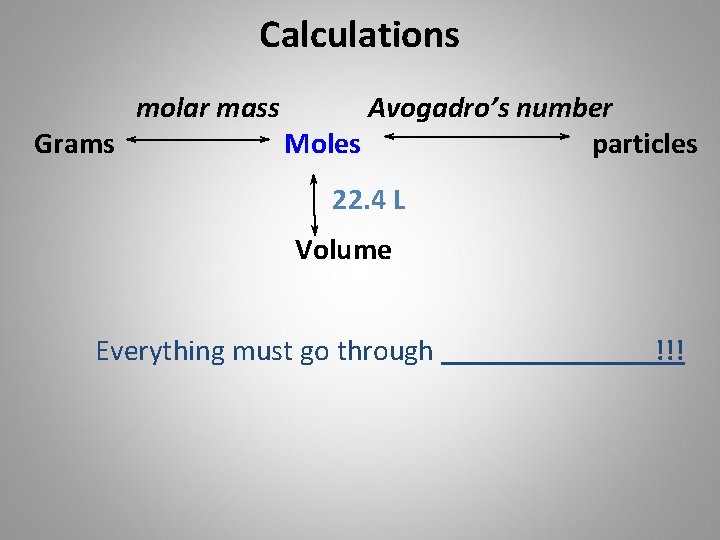
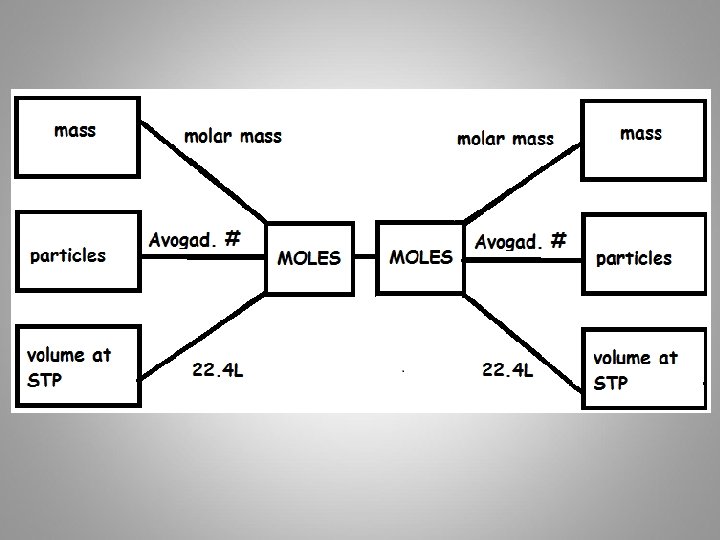
Calculations Grams molar mass Avogadro’s number Moles particles 22. 4 L Volume Everything must go through !!!

Chocolate Chip Cookies!! 1 cup butter 1 cup packed brown sugar 2 eggs 2 1/2 cups all-purpose flour 2 cups semisweet chocolate chips Makes 3 dozen How many eggs are needed to make 3 dozen cookies? How many eggs to make 9 dozen cookies? How much brown sugar would I need if I had 4 eggs?

Cookies and Chemistry…Huh!? !? • Just like chocolate chip cookies have recipes, chemists have recipes called • Instead of using cups and teaspoons, we use • Lastly, instead of eggs, butter, sugar, etc. we use

Chemistry Recipes • reactions tell us how much will react to get a – like the cookie recipe – Be sure you have a balanced equation before you start! • Ex: Na + Cl 2 Na. Cl • Reaction tells us by mixing 2 moles of sodium with 1 mole of chlorine we will get 2 moles of sodium chloride • What if we wanted 4 moles of Na. Cl? 10 moles? 50 moles?

Practice • Write the balanced reaction for hydrogen gas reacting with oxygen gas. H 2 + O 2 H 2 O – How many moles of reactants are needed? – What if we wanted 4 moles of water? – What if we had 3 moles of oxygen, how much hydrogen would we need to react, and how much water would we get? – What if we had 50 moles of hydrogen, how much oxygen would we need, and how much water produced?

Stoichiometry is… • Greek for “measuring elements” Pronounced “stoy kee ah muh tree” • Defined as: calculations of the quantities in chemical reactions, based on a balanced equation. • There are to interpret a balanced chemical equation

#1. In terms of Particles • An Element is made of • A Molecular compound (made of only nonmetals) is made up of • Ionic Compounds (made of a metal and nonmetal parts) are made of

Example: 2 H 2 + O 2 → 2 H 2 O • Two molecules of hydrogen and one molecule of oxygen form two molecules of water. • Another example: 2 Al 2 O 3 ® 4 Al + 3 O 2 Al 2 O 3 form 4 2 and 3 Al O 2 Now read this: 2 Na + 2 H 2 O ® 2 Na. OH + H 2

#2. In terms of Moles • tell us how many moles of each substance 2 Al 2 O 3 ® 4 Al + 3 O 2 – mol Al 2 O 3, mol Al, mol O 2 2 Na + 2 H 2 O ® 2 Na. OH + H 2 • Remember: A balanced equation is a

#3. In terms of Mass • The Law of Conservation of Mass applies • We can check mass by using moles. 1 mole Be Be + 2 F Be. F 2 1 mole Be = + 2 mole F 1 mole F = 36. 04 g H 2 + O 2 reactants

In terms of Mass (for products) Be + 2 F Be. F 2 1 moles Be. F 2 47. 01 g Be. F 2 = 1 mole Be. F 2 g Be + 2 F = reactant = product Mass of reactants and products. must be

#4. In terms of Volume • At STP, 1 mol of any gas = 2 H 2 + O 2 ® 2 H 2 O (2 x 22. 4 L H 2) + (1 x 22. 4 L O 2) ® (2 x 22. 4 L H 2 O) 67. 2 Liters of reactant ≠ 44. 8 Liters of product! ** are ALWAYS and however, molecules, formula units, moles, and volumes will not necessarily be conserved!

Practice: • Show that the following equation follows the Law of Conservation of Mass (show the atoms balance, and the mass on both sides is equal) 2 Al 2 O 3 ® 4 Al + 3 O 2 Atoms: Al and O = Al and Mass: Reactant: g/mol = Products: 108 g/mol + 204 g/mol O

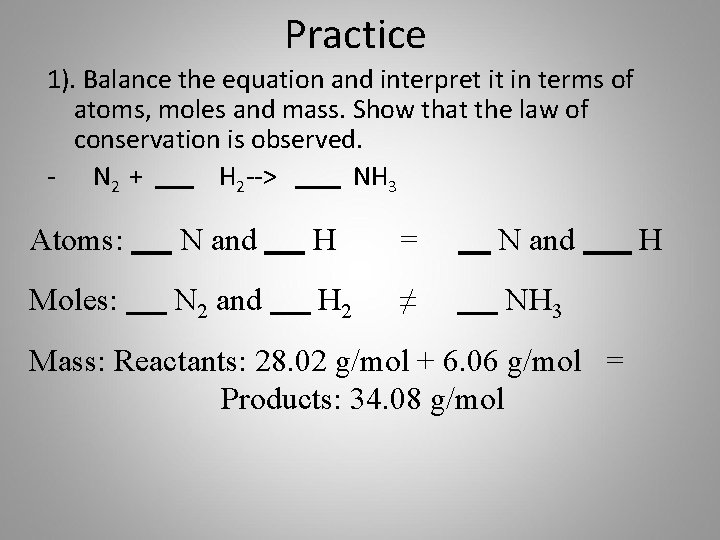
Practice 1). Balance the equation and interpret it in terms of atoms, moles and mass. Show that the law of conservation is observed. - N 2 + H 2 --> NH 3 Atoms: N and H = N and Moles: N 2 and H 2 ≠ NH 3 Mass: Reactants: 28. 02 g/mol + 6. 06 g/mol = Products: 34. 08 g/mol H

Section 12. 2 Chemical Calculations

Mole to Mole conversions 2 Al 2 O 3 ® 4 Al + 3 O 2 – each time we use 2 moles of Al 2 O 3 we will also make 3 moles of O 2 2 moles Al 2 O 3 3 mole O 2 or 3 mole O 2 2 moles Al 2 O 3 This is how we can convert from mols to mols. This is why we need balanced equations.

Mole to Mole conversions • How many moles of O 2 are produced when 3. 34 moles of Al 2 O 3 decompose? 2 Al 2 O 3 ® 4 Al + 3 O 2 3. 34 mol Al 2 O 3 = Conversion factor from balanced equation If you know the amount of ANY chemical in the reaction, you can find the amount of ALL the other chemicals!

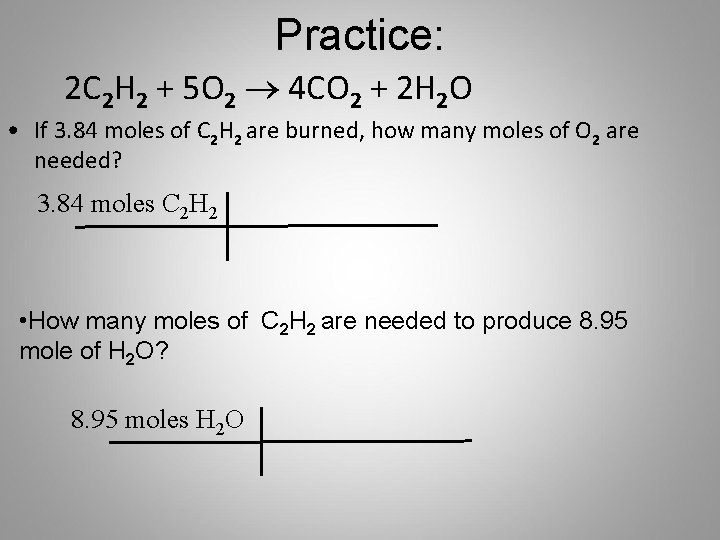
Practice: 2 C 2 H 2 + 5 O 2 ® 4 CO 2 + 2 H 2 O • If 3. 84 moles of C 2 H 2 are burned, how many moles of O 2 are needed? 3. 84 moles C 2 H 2 • How many moles of C 2 H 2 are needed to produce 8. 95 mole of H 2 O? 8. 95 moles H 2 O

Steps to Calculate Stoichiometric Problems 1. 2. 3. 4. Correctly the equation. Convert the given amount into. Set up mole. Use mole ratios to calculate moles of desired chemical. 5. Convert moles back into final unit.

Mole-Mass Conversions • Most of the time in chemistry, the amounts are given in grams instead of moles • We still use the mole ratio, but now we also use to get to • Example: How many grams of chlorine are required to react with 5. 00 moles of sodium to produce sodium chloride? 2 Na + Cl 2 2 Na. Cl 5. 00 moles Na 1 mol Cl 2 70. 90 g Cl 2 2 mol Na 1 mol Cl 2

Practice • Calculate the mass in grams of Iodine required to react completely with 0. 50 moles of aluminum. Al + 3 I Al. I 3 0. 50 mol Al

Mass-Mole • We can also start with mass and convert to moles • We use molar mass and the mole ratio to get to moles of the compound of interest – Calculate the number of moles of ethane (C 2 H 6) needed to produce 10. 0 g of water – 2 C 2 H 6 + 7 O 2 4 CO 2 + 6 H 20 10. 0 g H 2 O

Practice • Calculate how many moles of oxygen are required to make 10. 0 g of aluminum oxide • 2 Al + 3 O Al 2 O 3 10. 0 g Al 2 O 3

Mass-Mass Problem: 6. 50 grams of aluminum reacts with oxygen. How many grams of aluminum oxide are formed? 4 Al + 3 O 2 2 Al 2 O 3 6. 50 g Al 1 mol Al 26. 98 g Al (6. 50 x 1 x 2 x 101. 96) ÷ (26. 98 x 4 x 1) = = ? g Al 2 O 3

Another example: • If 10. 1 g of Fe are added to a solution of Copper (II) Sulfate, how many grams of solid copper would form? 2 Fe + 3 Cu. SO 4 ® Fe 2(SO 4)3 + 3 Cu 10. 1 g Fe 1 mol Fe 63. 55 g Cu 55. 85 g Fe 1 mol Cu

Volume-Volume Calculations: • How many liters of CH 4 at STP are required to completely react with 17. 5 L of O 2 ? CH 4 + 2 O 2 ® CO 2 + 2 H 2 O 1 mol O 2 1 mol CH 4 22. 4 L CH 4 17. 5 L O 2 22. 4 L O 2 2 mol O 2 1 mol CH 4

Section 12. 3 Limiting Reagent & Percent Yield • OBJECTIVES: –Identify the limiting reagent in a reaction.

“Limiting” Reagent • If you are given one dozen loaves of bread, a gallon of mustard, and three pieces of salami, how many salami sandwiches can you make? • The is the reactant you run out of first. • The is the one you have left over. • The limiting reagent how much product you can make

How do you find out which is limited? • The chemical that makes the amount of is the “limiting reagent”. • Limiting reagent problems will give you 2 amounts of chemicals • You must do stoichiometry problems; one for each reagent given. • If 2 products are given, pick one and use it for both calculations

• If 10. 6 g of copper reacts with 3. 83 g sulfur, how many grams of the product (copper (I) sulfide) will be formed? 2 Cu + S ® Cu 2 S 1 mol Cu 2 S 159. 16 g Cu 2 S 1 mol Cu 10. 6 g Cu 63. 55 g Cu 2 mol Cu 1 mol Cu 2 S = 13. 3 g Cu 2 S 1 mol Cu 2 S 159. 16 g Cu 2 S 32. 06 g S 1 mol Cu 2 S 1 mol S 3. 83 g S = 19. 0 g Cu 2 S

Finding the Amount of Excess • By calculating the amount of the reactant needed to completely react with the limiting reactant, we can subtract that amount from the given amount to find the amount of excess. • Can we find the amount of excess potassium in the next problem?

Finding Excess Practice • 15. 0 g of potassium reacts with 15. 0 g of iodine. 2 K + I 2 2 KI • We found that Iodine is the limiting reactant. 15. 0 g I 2 1 mol I 2 39. 1 g K 254 g I 2 1 mol K 15. 0 g K – 4. 62 g K = Given amount of excess reactant Amount of excess reactant actually used Note that we started with the limiting reactant! Once you determine the LR, you should only start with it!

Another example: • If 10. 3 g of aluminum are reacted with 51. 7 g of Cu. SO 4, how much copper (grams) will be produced? 2 Al + 3 Cu. SO 4 → 3 Cu + Al 2(SO 4)3 10. 3 g Al 1 mol Al 26. 98 g Al 51. 7 g Cu. SO 4 1 mol Cu. SO 4 159. 62 g Cu. SO 4 63. 55 g Cu 1 mol Cu

How much excess reactant do we have from the last problem? • Cu. SO 4 limiting reactant 51. 7 g Cu. SO 4 1 mol Cu. SO 4 159. 62 g Cu. SO 4 • Excess Al = 26. 98 g Al 1 mol Al

Limiting Reactant: Recap 1. You can recognize a limiting reactant problem because there is MORE THAN ONE GIVEN AMOUNT. 2. Convert ALL of the reactants to the SAME product (pick any product you choose. ) 3. The lowest answer is the limiting reactant 4. The other reactant(s) are in EXCESS. 5. To find the amount of excess, subtract the amount used from the given amount. 6. If you have to find more than one product, be sure to start with the limiting reactant. You don’t have to determine which is the LR over and over again!

The Concept of: A little different type of yield than you had in Driver’s Education class.

What is Yield? • Yield is the amount of product made in a chemical reaction. • There are three types: 1. Theoretical yield- what the balanced equation tells be made 2. yield- what you actually get in the lab when the chemicals are mixed 3. Percent yield =

Example: • 6. 78 g of copper is produced when 3. 92 g of Al are reacted with excess copper (II) sulfate. 2 Al + 3 Cu. SO 4 ® Al 2(SO 4)3 + 3 Cu • What is the actual yield? • What is theoretical yield? 3. 92 g Al 1 mol Al 26. 98 g Al What is the percent yield? X 100 63. 55 mol Cu 1 mol Cu

Details on Yield • Percent yield tells us how “efficient” a reaction is. • Percent yield can not be bigger than 100 %. • Theoretical yield will always be larger than actual yield! – Why? Due to impure reactants; competing side reactions; loss of product in filtering or transferring between containers; measuring