Chapter 12 PPT Surface Area and Volume Prepared

Chapter 12 PPT Surface Area and Volume Prepared by Mrs. Pullo for her Geometry Students

Three-Dimensional Figures and Nets A net is a twodimensional pattern that you can fold to form a three-dimensional figure. A polyhedron is a threedimensional figure whose surfaces are polygons. The polygons are the faces of the polyhedron. An edge is a segment that is the intersection of two faces. A vertex is a point where edges intersect. faces edge vertex

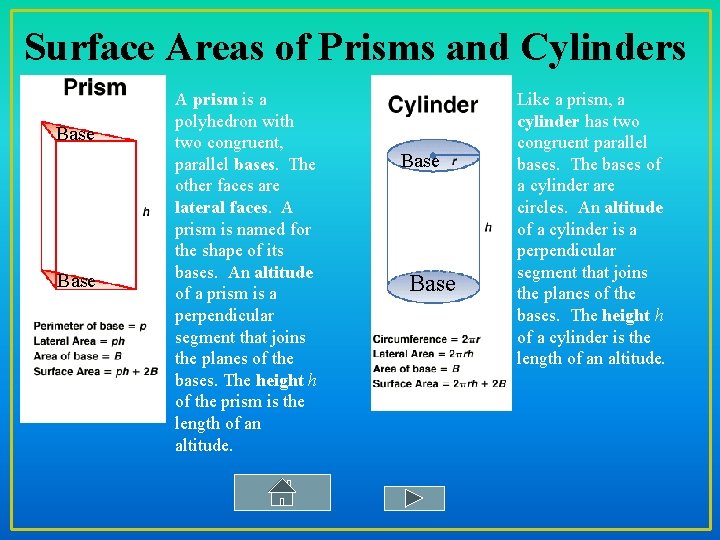
Surface Areas of Prisms and Cylinders Base A prism is a polyhedron with two congruent, parallel bases. The other faces are lateral faces. A prism is named for the shape of its bases. An altitude of a prism is a perpendicular segment that joins the planes of the bases. The height h of the prism is the length of an altitude. Base Like a prism, a cylinder has two congruent parallel bases. The bases of a cylinder are circles. An altitude of a cylinder is a perpendicular segment that joins the planes of the bases. The height h of a cylinder is the length of an altitude.

Lateral and Surface Areas of a Right Prism Total Surface are = Lateral area + 2 times the area of the bases (T = L + 2 B) The Lateral area = Perimeter of base x height of the polyhedron 2 B = area of the base times 2 because there are two bases in a prism

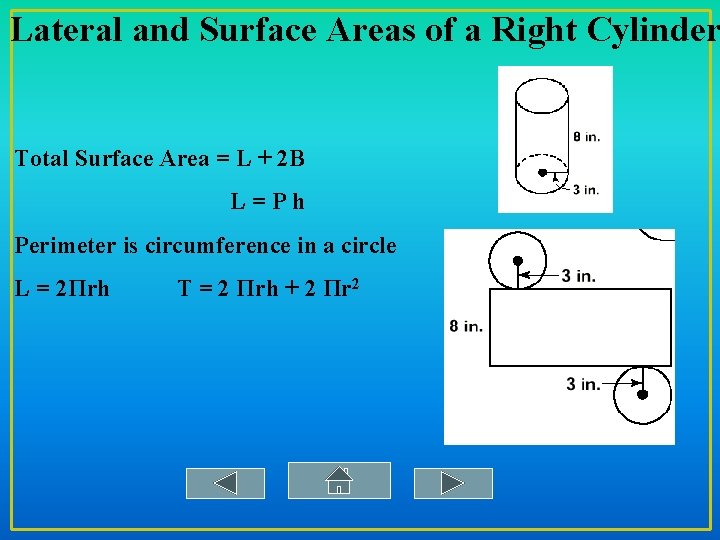
Lateral and Surface Areas of a Right Cylinder Total Surface Area = L + 2 B L=Ph Perimeter is circumference in a circle L = 2Πrh T = 2 Πrh + 2 Πr 2

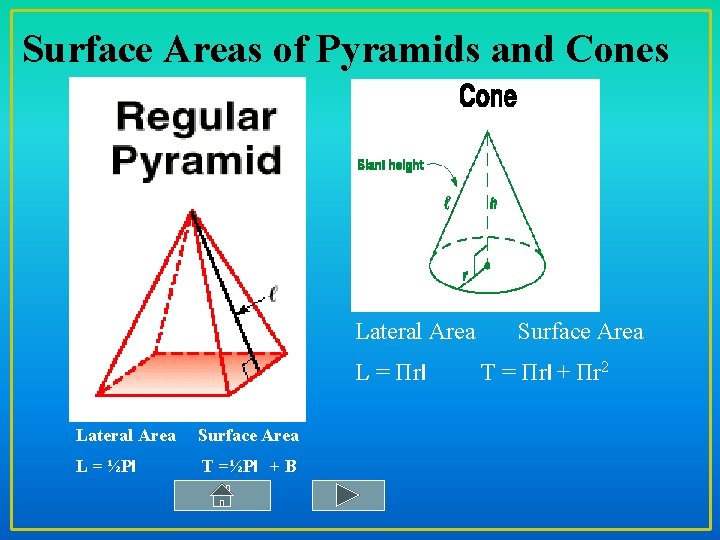
Surface Areas of Pyramids and Cones Lateral Area L = Πrl Lateral Area Surface Area L = ½Pl T =½Pl + B Surface Area T = Πrl + Πr 2

Volumes of Prisms and Cylinders This is a trapezoidal prism because it base is a trapezoid V V= 1/2 h(b + b) times height of object

Volume of a Rectangular Prism V = Bh B = length times width So, V = lwh example

Volume of a Cylinder V= Bh B = Πr 2 V = Πr 2 h example

Volumes of Prisms and Cylinders Example

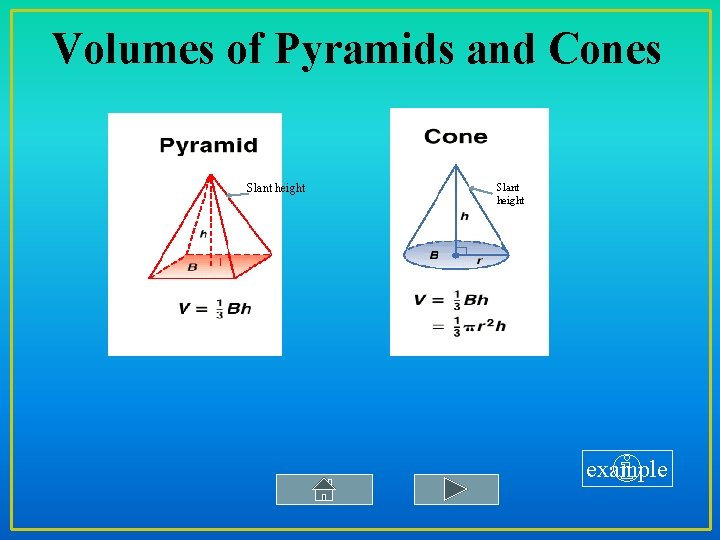
Volumes of Pyramids and Cones Slant height example

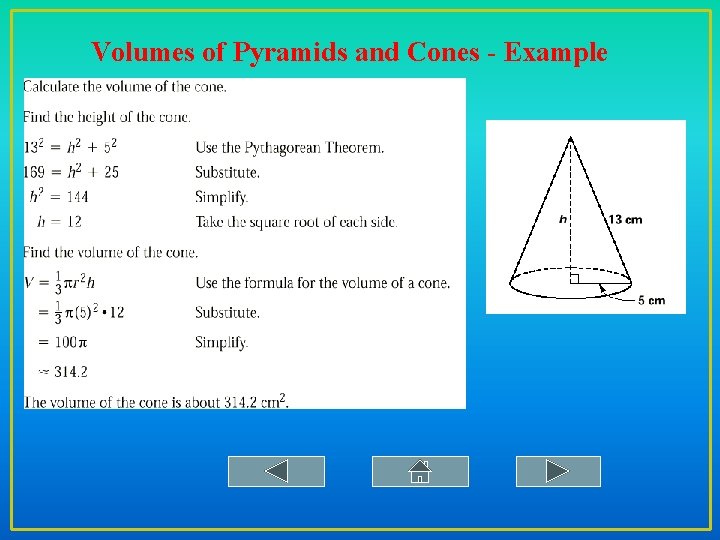
Volumes of Pyramids and Cones - Example

Surface Areas and Volumes of Spheres Fin Sub T 52 The 3

In a Nut Shell Volume is the area of the base times the ⊥ height in a prism and 1/3 of the area of the base times the ⊥ height in a pyramid or cone Finding the area of the base depends on the shape Surface area is the lateral area plus the area of the base(s) Lateral area is the perimeter of the base times the ⊥ height And the area of the bases depends on the shape of the base