CHAPTER 12 Multiway Search Trees Java Software Structures

CHAPTER 12: Multi-way Search Trees Java Software Structures: Designing and Using Data Structures Third Edition John Lewis & Joseph Chase Addison Wesley is an imprint of Modified by Chuck Cusack, Hope College © 2010 Pearson Addison-Wesley. All rights reserved.

Chapter Objectives • Examine 2 -3 and 2 -4 trees • Introduce the generic concept of a B-tree • Examine some specialized implementations of B-trees 1 -2 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -2

Multi-way Search Trees • In a multi-way search tree, – each node may have more than two child nodes – there is a specific ordering relationship among the nodes • In this chapter, we examine three forms of multiway search trees – 2 -3 trees – 2 -4 trees – B-trees 1 -3 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -3

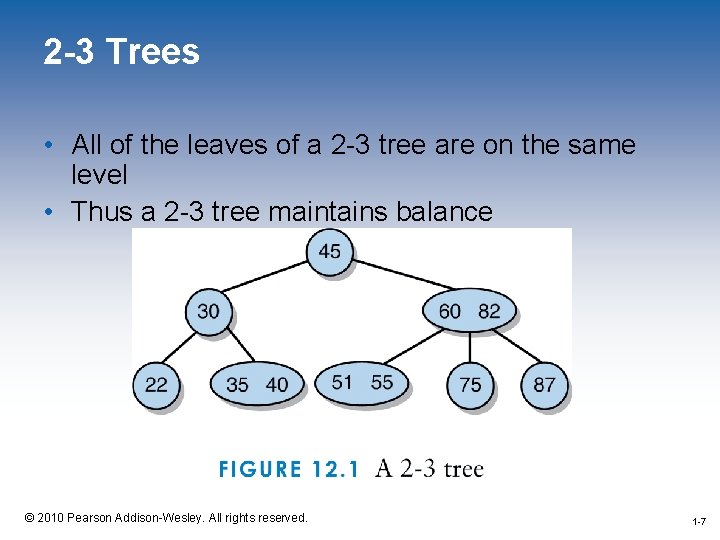
2 -3 Trees • A 2 -3 tree is a multi-way search tree in which each node has zero, two, or three children • A node with zero or two children is called a 2 -node • A node with zero or three children is called a 3 -node 1 -4 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -4

2 -3 Trees: 2 -Nodes • A 2 -node contains one element and either has no children or two children – Elements of the left sub-tree less than the element – Elements of the right sub-tree greater than or equal to the element 1 -5 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -5

2 -3 Trees: 3 -Nodes • A 3 -node contains two elements, one designated as the smaller and one as the larger • A 3 -node has either no children or three children • If a 3 -node has children then – Elements of the left sub-tree are less than the smaller element – The smaller element is less than or equal to the elements of the middle sub-tree – Elements of the middle sub-tree are less then the larger element – The larger element is less than or equal to the elements of the right sub-tree 1 -6 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -6

2 -3 Trees • All of the leaves of a 2 -3 tree are on the same level • Thus a 2 -3 tree maintains balance 1 -7 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -7

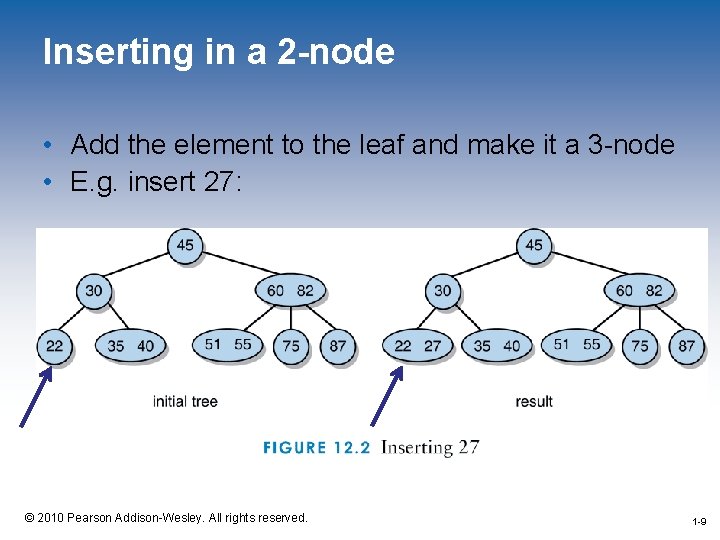
Inserting Elements into a 2 -3 Tree • All insertions into a 2 -3 tree occur at the leaves – The tree is searched to find the proper leaf for the new element • Insertion has three cases – Tree is empty • Create a new 2 -node, insert the element into the 2 -node, and make it the root. – Insertion point is a 2 -node (next slide) – Insertion point is a 3 -node (a few slides later) 1 -8 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -8

Inserting in a 2 -node • Add the element to the leaf and make it a 3 -node • E. g. insert 27: 1 -9 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -9

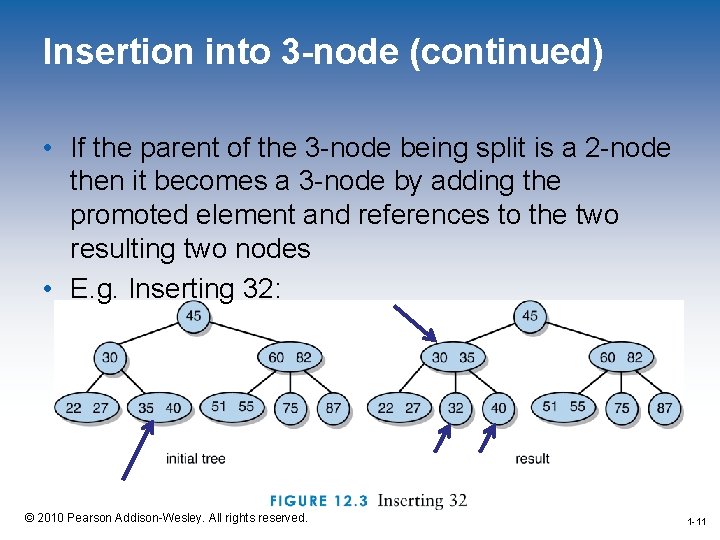
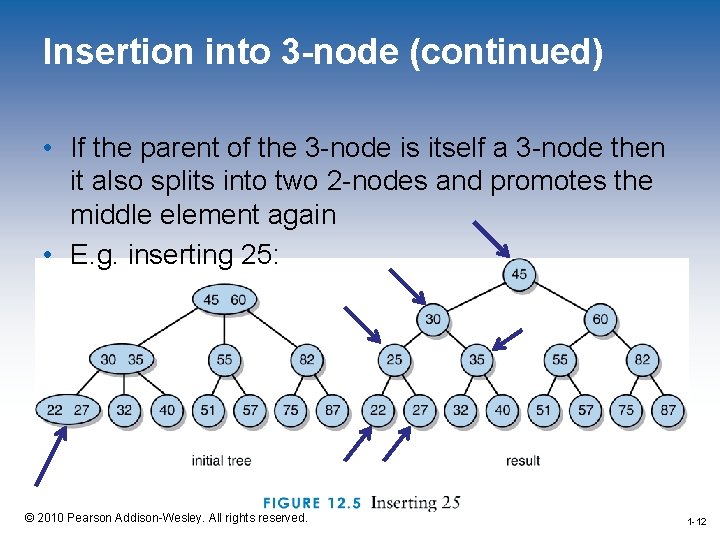
Inserting in a 3 -node • The 3 elements (the two old ones and the new one) are ordered • The 3 -node is split into two 2 -nodes, one for the smaller element and one for the larger element • The middle element is promoted (or propagated) up a level. There are 2 cases: – The parent of the 3 -node is a 2 -node – The parent of the 3 -node is a 3 -node 1 -10 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -10

Insertion into 3 -node (continued) • If the parent of the 3 -node being split is a 2 -node then it becomes a 3 -node by adding the promoted element and references to the two resulting two nodes • E. g. Inserting 32: 1 -11 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -11

Insertion into 3 -node (continued) • If the parent of the 3 -node is itself a 3 -node then it also splits into two 2 -nodes and promotes the middle element again • E. g. inserting 25: 1 -12 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -12

Removing Elements from a 2 -3 Tree • Removal of elements is also made up of three cases, based on the location of the element to be removed: – a leaf that is a 3 -node – a leaf that is a 2 -node – an internal node 1 -13 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -13

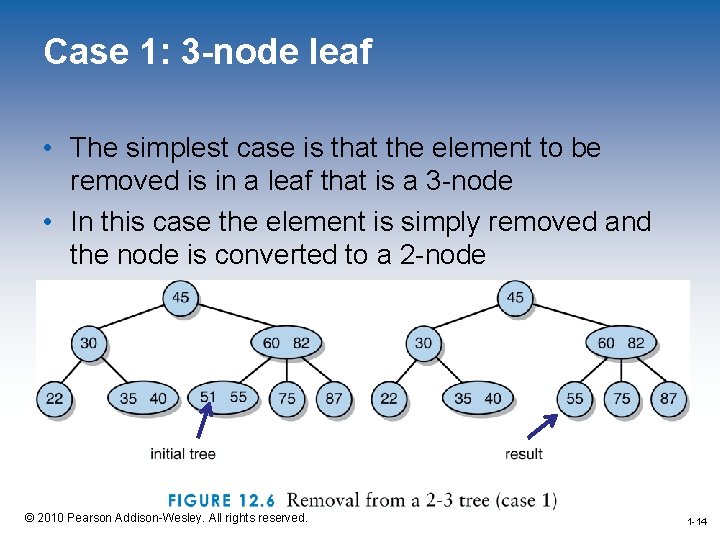
Case 1: 3 -node leaf • The simplest case is that the element to be removed is in a leaf that is a 3 -node • In this case the element is simply removed and the node is converted to a 2 -node 1 -14 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -14

Case 2: 2 -node leaf • This creates a situation called underflow • We must rotate the tree and/or reduce the tree’s height in order to maintain the properties of the 2 -3 tree • This case can be broken down into four subordinate cases 1 -15 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -15

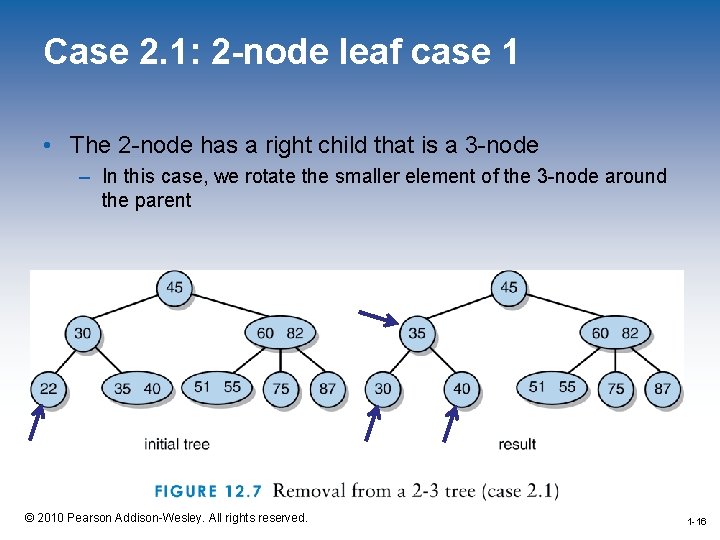
Case 2. 1: 2 -node leaf case 1 • The 2 -node has a right child that is a 3 -node – In this case, we rotate the smaller element of the 3 -node around the parent 1 -16 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -16

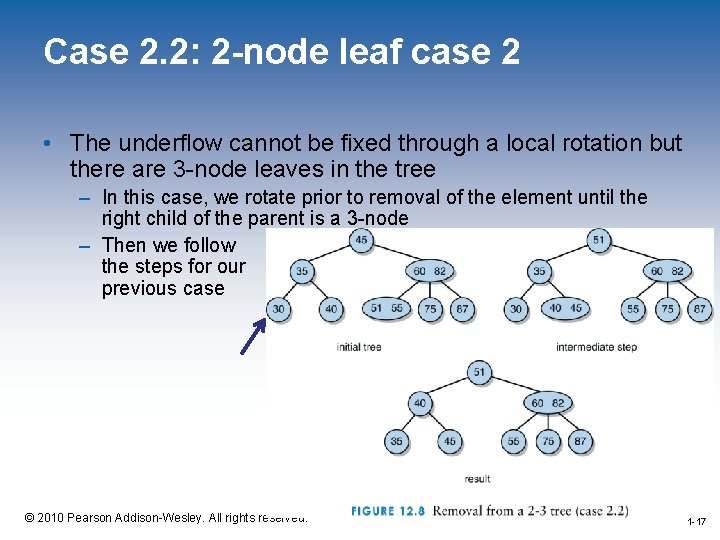
Case 2. 2: 2 -node leaf case 2 • The underflow cannot be fixed through a local rotation but there are 3 -node leaves in the tree – In this case, we rotate prior to removal of the element until the right child of the parent is a 3 -node – Then we follow the steps for our previous case 1 -17 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -17

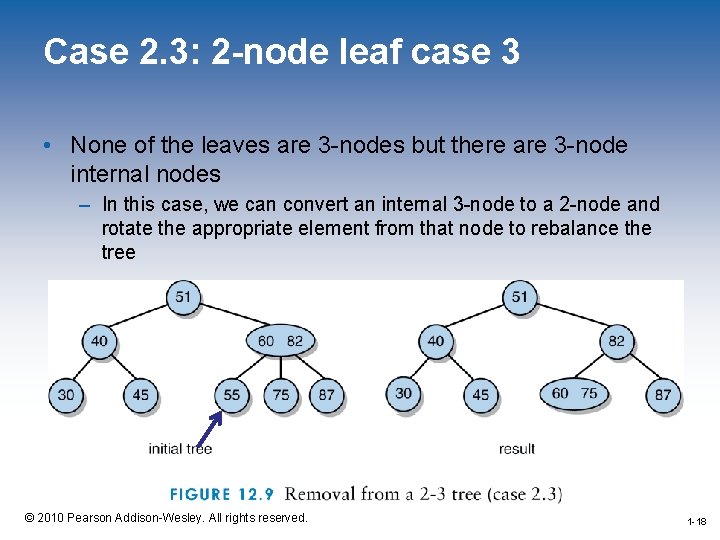
Case 2. 3: 2 -node leaf case 3 • None of the leaves are 3 -nodes but there are 3 -node internal nodes – In this case, we can convert an internal 3 -node to a 2 -node and rotate the appropriate element from that node to rebalance the tree 1 -18 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -18

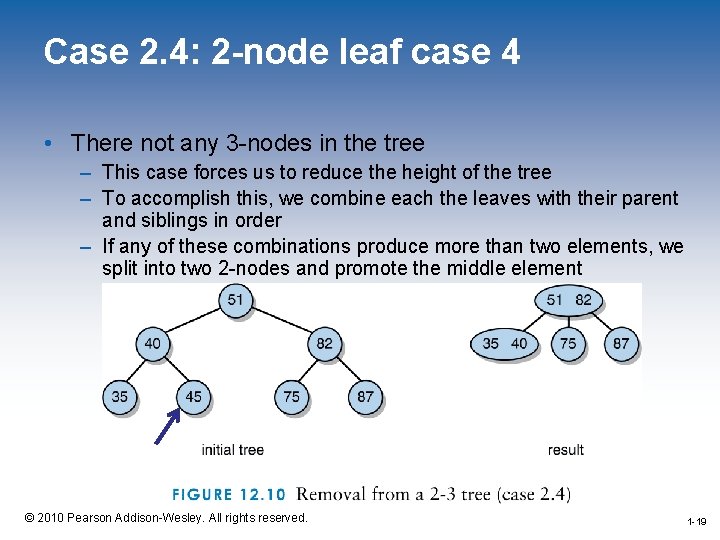
Case 2. 4: 2 -node leaf case 4 • There not any 3 -nodes in the tree – This case forces us to reduce the height of the tree – To accomplish this, we combine each the leaves with their parent and siblings in order – If any of these combinations produce more than two elements, we split into two 2 -nodes and promote the middle element 1 -19 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -19

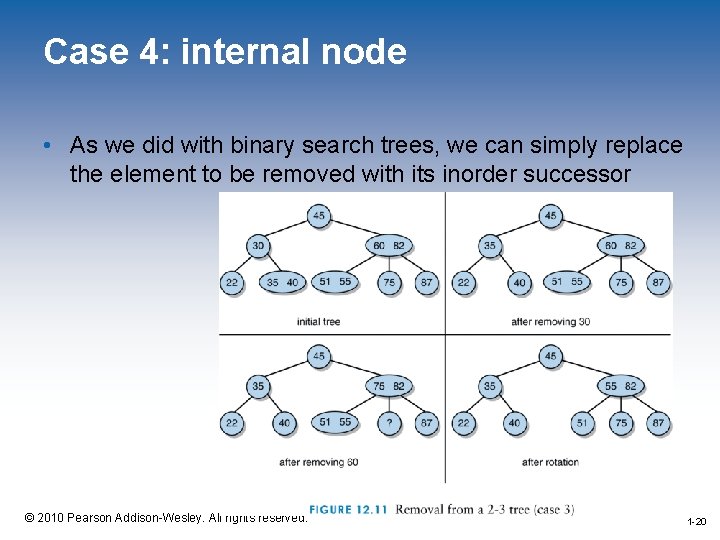
Case 4: internal node • As we did with binary search trees, we can simply replace the element to be removed with its inorder successor 1 -20 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -20

2 -4 Trees • 2 -4 Trees are very similar to 2 -3 Trees adding the characteristic that a node can contain three elements • A 4 -node contains three elements and has either no children or 4 children • The same ordering property applies as 2 -3 trees • The same cases apply to both insertion and removal of elements as illustrated on the following slides 1 -21 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -21

B-Trees • Both 2 -3 trees and 2 -4 trees are examples of a larger class of multi-way search trees called B-trees • We refer to the maximum number of children of each node as the order of a B-Tree • Thus 2 -3 trees are 3 B-trees and 2 -4 trees are 4 B-trees • B-trees of order m have the following properties: 1 -22 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -22

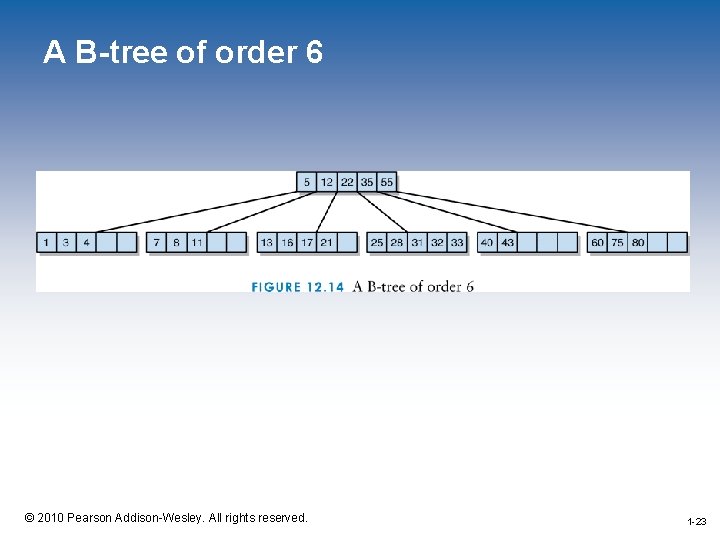
A B-tree of order 6 1 -23 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -23

Motivation for B-trees • To make the most efficient use of the relationship between main memory and secondary storage • Until now, we have assumed that an entire collection (data structure) exists in memory at once • What if the collection is too large to fit in memory? • B-trees were designed to flatten the tree structure and to allow for larger blocks of data that could then be tuned so that the size of a node is the same size as a block on secondary storage • This reduces the number of nodes and/or blocks that must be accessed, thus improving performance 1 -24 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -24

B*-trees • A variation of B-trees called B*-trees were created to solve the problem that the B-tree could be half empty at any given time • B*-trees have all of the properties as B-trees except: – in a B*-tree, each node has k children where (2 m– 1)/3 ≤ k ≤ m • (Recall that for a B-tree it was: m/2 ≤ k ≤ m) • This means that each non-root node is at least two-thirds full 1 -25 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -25

B+-trees • Another potential problem for B-trees is sequential access • B+-trees provide a solution to this problem by requiring that each element appear in a leaf regardless of whether it appears in an internal node • By requiring this and then linking the leaves together, B+trees provide very efficient sequential access while maintaining many of the benefits of a tree structure 1 -26 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -26