Chapter 12 Multiple Regression Multiple Regression Numeric Response

Chapter 12 Multiple Regression

Multiple Regression • Numeric Response variable (y) • k Numeric predictor variables (k < n) • Model: Y = b 0 + b 1 x 1 + + bkxk + e Partial Regression Coefficients: bi effect (on the mean response) of increasing the ith predictor variable by 1 unit, holding all other predictors constant • Model Assumptions (Involving Error terms e ) • – Normally distributed with mean 0 – Constant Variance s 2 – Independent (Problematic when data are series in time/space)

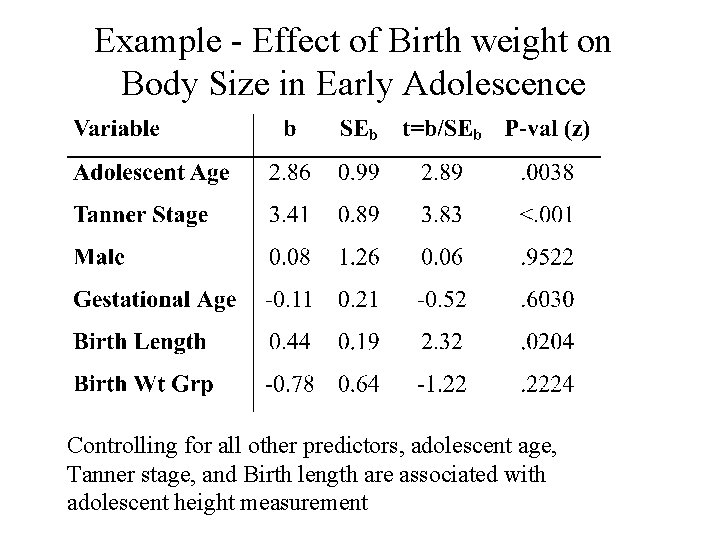
Example - Effect of Birth weight on Body Size in Early Adolescence • Response: Height at Early adolescence (n =250 cases) • Predictors (k=6 explanatory variables) • Adolescent Age (x 1, in years -- 11 -14) • Tanner stage (x 2, units not given) • Gender (x 3=1 if male, 0 if female) • Gestational age (x 4, in weeks at birth) • Birth length (x 5, units not given) • Birthweight Group (x 6=1, . . . , 6 <1500 g (1), 15001999 g(2), 2000 -2499 g(3), 2500 -2999 g(4), 30003499 g(5), >3500 g(6)) Source: Falkner, et al (2004)

Least Squares Estimation • Population Model for mean response: • Least Squares Fitted (predicted) equation, minimizing SSE: • All statistical software packages/spreadsheets can compute least squares estimates and their standard errors

Analysis of Variance • Direct extension to ANOVA based on simple linear regression • Only adjustments are to degrees of freedom: – DFR = k DFE = n-(k+1)

Testing for the Overall Model - F-test • Tests whether any of the explanatory variables are associated with the response • H 0: b 1= =bk=0 (None of the xs associated with y) • HA: Not all bi = 0

Example - Effect of Birth weight on Body Size in Early Adolescence • Authors did not print ANOVA, but did provide following: • n=250 k=6 R 2=0. 26 • H 0: b 1= =b 6=0 HA: Not all bi = 0

Testing Individual Partial Coefficients - t-tests • Wish to determine whether the response is associated with a single explanatory variable, after controlling for the others • H 0: bi = 0 HA: bi 0 (2 -sided alternative)

Example - Effect of Birth weight on Body Size in Early Adolescence Controlling for all other predictors, adolescent age, Tanner stage, and Birth length are associated with adolescent height measurement

Comparing Regression Models • Conflicting Goals: Explaining variation in Y while keeping model as simple as possible (parsimony) • We can test whether a subset of k-g predictors (including possibly cross-product terms) can be dropped from a model that contains the remaining g predictors. H 0: bg+1=…=bk =0 – Complete Model: Contains all k predictors – Reduced Model: Eliminates the predictors from H 0 – Fit both models, obtaining sums of squares for each (or R 2 from each): • Complete: SSRc , SSEc (Rc 2) • Reduced: SSRr , SSEr (Rr 2)

Comparing Regression Models • H 0: bg+1=…=bp = 0 (After removing the effects of X 1, …, Xg, none of other predictors are associated with Y) • Ha: H 0 is false P-value based on F-distribution with k-g and n-(k+1) d. f.

Models with Dummy Variables • Some models have both numeric and categorical explanatory variables (Recall gender in example) • If a categorical variable has m levels, need to create m-1 dummy variables that take on the values 1 if the level of interest is present, 0 otherwise. • The baseline level of the categorical variable is the one for which all m-1 dummy variables are set to 0 • The regression coefficient corresponding to a dummy variable is the difference between the mean for that level and the mean for baseline group, controlling for all numeric predictors

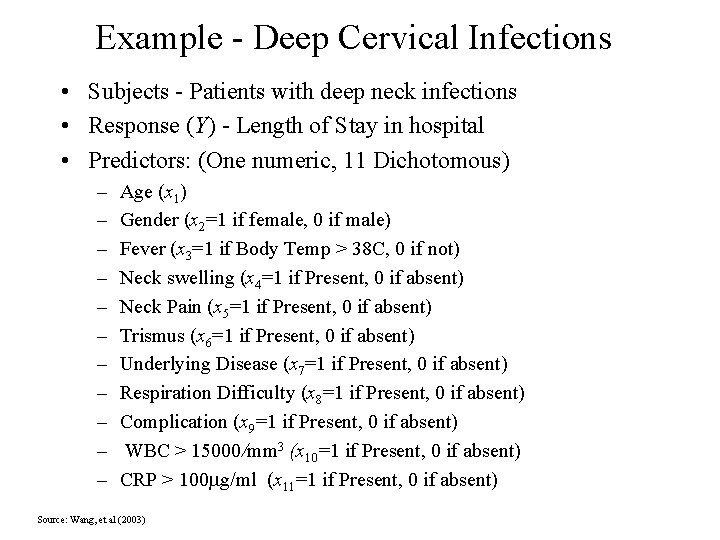
Example - Deep Cervical Infections • Subjects - Patients with deep neck infections • Response (Y) - Length of Stay in hospital • Predictors: (One numeric, 11 Dichotomous) – – – Age (x 1) Gender (x 2=1 if female, 0 if male) Fever (x 3=1 if Body Temp > 38 C, 0 if not) Neck swelling (x 4=1 if Present, 0 if absent) Neck Pain (x 5=1 if Present, 0 if absent) Trismus (x 6=1 if Present, 0 if absent) Underlying Disease (x 7=1 if Present, 0 if absent) Respiration Difficulty (x 8=1 if Present, 0 if absent) Complication (x 9=1 if Present, 0 if absent) WBC > 15000/mm 3 (x 10=1 if Present, 0 if absent) CRP > 100 mg/ml (x 11=1 if Present, 0 if absent) Source: Wang, et al (2003)

Example - Weather and Spinal Patients • Subjects - Visitors to National Spinal Network in 23 cities Completing SF-36 Form • Response - Physical Function subscale (1 of 10 reported) • Predictors: – – – – – Source: Glaser, et al (2004) Patient’s age (x 1) Gender (x 2=1 if female, 0 if male) High temperature on day of visit (x 3) Low temperature on day of visit (x 4) Dew point (x 5) Wet bulb (x 6) Total precipitation (x 7) Barometric Pressure (x 7) Length of sunlight (x 8) Moon Phase (new, wax crescent, 1 st Qtr, wax gibbous, full moon, wan gibbous, last Qtr, wan crescent, presumably had 8 -1=7 dummy variables)

Modeling Interactions • Statistical Interaction: When the effect of one predictor (on the response) depends on the level of other predictors. • Can be modeled (and thus tested) with crossproduct terms (case of 2 predictors): – E(Y) = a + b 1 X 1 + b 2 X 2 + b 3 X 1 X 2 – X 2=0 E(Y) = a + b 1 X 1 – X 2=10 E(Y) = a + b 1 X 1 + 10 b 2 + 10 b 3 X 1 = (a + 10 b 2) + (b 1 + 10 b 3)X 1 • The effect of increasing X 1 by 1 on E(Y) depends on level of X 2, unless b 3=0 (t-test)

Logistic Regression • Logistic Regression - Binary Response variable and numeric and/or categorical explanatory variable(s) – Goal: Model the probability of a particular outcome as a function of the predictor variable(s) – Problem: Probabilities are bounded between 0 and 1

Logistic Regression with 1 Predictor • Response - Presence/Absence of characteristic • Predictor - Numeric variable observed for each case • Model - p (x) Probability of presence at predictor level x • b = 0 P(Presence) is the same at each level of x • b > 0 P(Presence) increases as x increases • b < 0 P(Presence) decreases as x increases

Logistic Regression with 1 Predictor · b 0, b 1 are unknown parameters and must be estimated using statistical software such as SPSS, SAS, or STATA · Primary interest in estimating and testing hypotheses regarding b 1 · Large-Sample test (Wald Test): (Some software runs z-test) · H 0: b 1 = 0 H A: b 1 0

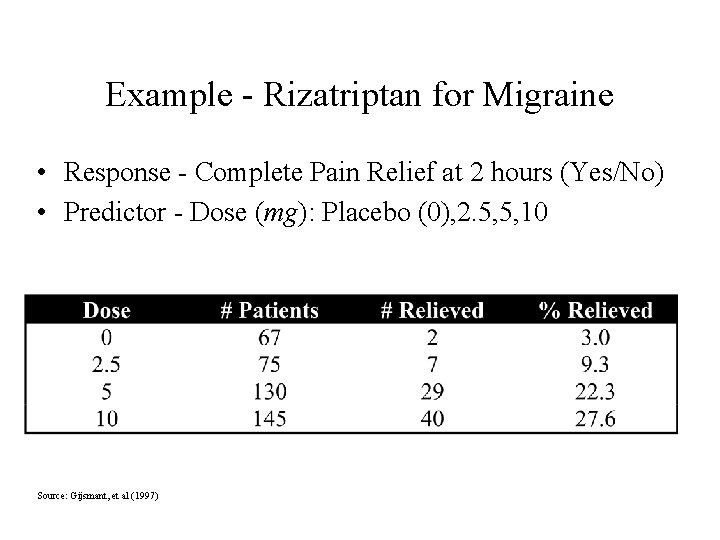
Example - Rizatriptan for Migraine • Response - Complete Pain Relief at 2 hours (Yes/No) • Predictor - Dose (mg): Placebo (0), 2. 5, 5, 10 Source: Gijsmant, et al (1997)

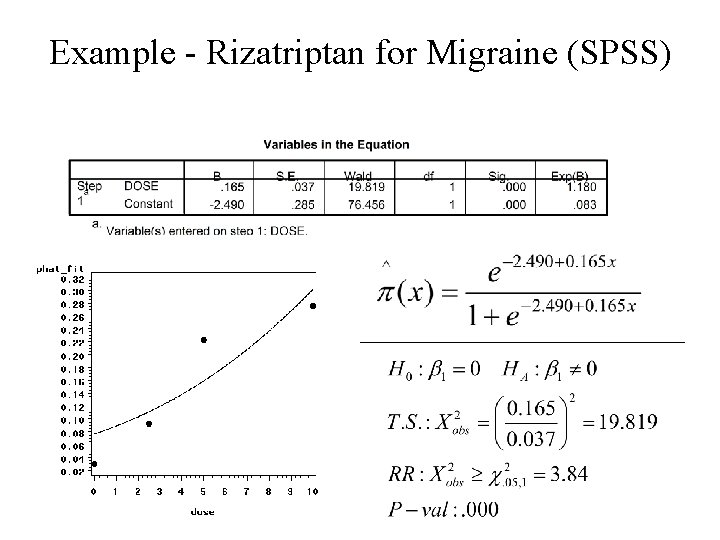
Example - Rizatriptan for Migraine (SPSS)

Odds Ratio • Interpretation of Regression Coefficient (b 1): – In linear regression, the slope coefficient is the change in the mean response as x increases by 1 unit – In logistic regression, we can show that: • Thus eb 1 represents the change in the odds of the outcome (multiplicatively) by increasing x by 1 unit • If b 1=0, the odds (and probability) are equal at all x levels (eb 1=1) • If b 1>0 , the odds (and probability) increase as x increases (eb 1>1) • If b 1< 0 , the odds (and probability) decrease as x increases (eb 1<1)

95% Confidence Interval for Odds Ratio • Step 1: Construct a 95% CI for b : • Step 2: Raise e = 2. 718 to the lower and upper bounds of the CI: • If entire interval is above 1, conclude positive association • If entire interval is below 1, conclude negative association • If interval contains 1, cannot conclude there is an association

Example - Rizatriptan for Migraine • 95% CI for b 1: • 95% CI for population odds ratio: • Conclude positive association between dose and probability of complete relief

Multiple Logistic Regression • Extension to more than one predictor variable (either numeric or dummy variables). • With p predictors, the model is written: • Adjusted Odds ratio for raising xi by 1 unit, holding all other predictors constant: • Inferences on bi and ORi are conducted as was described above for the case with a single predictor

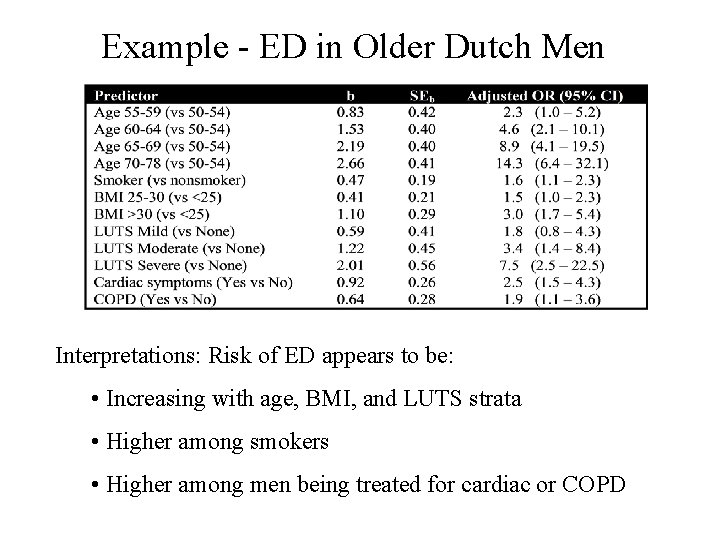
Example - ED in Older Dutch Men • Response: Presence/Absence of ED (n=1688) • Predictors: (k=12) – Age stratum (50 -54*, 55 -59, 60 -64, 65 -69, 70 -78) – Smoking status (Nonsmoker*, Smoker) – BMI stratum (<25*, 25 -30, >30) – Lower urinary tract symptoms (None*, Mild, Moderate, Severe) – Under treatment for cardiac symptoms (No*, Yes) – Under treatment for COPD (No*, Yes) * Baseline group for dummy variables Source: Blanker, et al (2001)

Example - ED in Older Dutch Men Interpretations: Risk of ED appears to be: • Increasing with age, BMI, and LUTS strata • Higher among smokers • Higher among men being treated for cardiac or COPD