Chapter 12 Linear Kinetics of Human Movement Part

Chapter 12 Linear Kinetics of Human Movement – Part 3 Basic Biomechanics, 4 th edition Susan J. Hall Presentation Created by TK Koesterer, Ph. D. , ATC Humboldt State University

WORK Work done on a body by a force is equal to the product of its magnitude and the distance the body moves in the direction of the force. Work = Force magnitude x Distance moved W = Fd • Positive work: motion in same direction as applied force (concentric) • Negative work: motion in opposite direction as applied force (eccentric) • Common units: joule (J) J = Nm =. 7376 ft∙lb Mechanical work caloric expenditure This is a jewel

Sample Work Problem • A weight lifter performs a two-hand snatch, a lift in which a barbell is raised overhead in one continuous motion. If he lifts 60 kg upward, 2 meters, what amount of work did he perform? 60 kg x 9. 81 m/s 2 = 589 N (F = ma) 589 N x 2 m = 1178 Nm or Joules • The weight lifter holds the 60 kg barbell overhead. How much work does he perform? 589 N x 0 m = 0 Nm or Joules

Sample Work Problem • Adrian has a body mass of 76 kg and has an arm length of 61 cm (distance from chin to bar). If he performs 10 pull-ups, what amount of work did he perform? 76 kg x 9. 81 m/s 2 = 745. 5 N x 0. 61 m = 454. 8 Nm or J • How much work does Adrian perform on his descent? Eccentric contraction is negative work.

POWER Power: rate at which mechanical work is performed Power = Work = W change in time t Power = force x distance = Fd change in time t Since v = d / t, Power = Fv Units: watts (W) 1 W = 1 J/s English Units: horsepower 1 hp = 550 ft·lb/s

Sample Power Problem • Brianna bounded up the six steps covering 1. 05 meters in 0. 75 seconds. She weighs 598 N (61 kg). How much mechanical power does she generate? • W = Fd 61 kg x 9. 81 m/s 2 x 1. 05 m 627. 9 Nm or J • P = W/t 627. 9 J / 0. 75 s = 837. 2 J/s or Watts

ENERGY Energy: the capacity to do work Forms: mechanical, chemical, nuclear, heat, etc. Mechanical energy is capacity to do mechanical work. Units are the same as work: joules

ENERGY Kinetic energy (KE): energy of motion • KE = ½ mv 2 = ½ kg ∙ (m 2/s 2) = ½ kg ∙ m/s 2 ∙ m = ½ mass ∙a∙ distance • KE = ½ Force ∙ distance (N ∙ m or J) Potential energy (PE): energy by virtue of a body’s position or configuration • PE = (wt)(h) = N ∙ m (J) or lb ∙ ft • PE = magh

Potential Energy due to position or composition. Stored Energy.

Potential Energy • Which has more potential energy? Gas has chemical Climber is high up, potential energy. so she has potential energy • Boulder has nowhere to go so no potential energy A gallon of gas can move a car 30 miles, but a rock climber landing on a car won’t really move it much at all.

Sample Potential Energy Problem • What is the potential energy of a 75 kg barbell lifted and held at a height of 2 m? • PE = magh PE = 75 kg x 9. 81 m/s 2 x 2 m =1471 Nm

Strain Energy Strain energy (SE): capacity to do work by virtue of a deformed body’s return to its original shape A form of potential energy • SE = 1/2 kx 2 k=constant x = distance over which the material is deformed

Kinetic Energy • Kinetic energy is the energy of things in motion: • Kinetic energy = 1/2 mass x velocity 2 • Which has more kinetic energy? Velocity is 1800 km/hour mass is 10 grams 10 times more energy than the baseball Not moving no kinetic energy 140 km/hour 145 grams

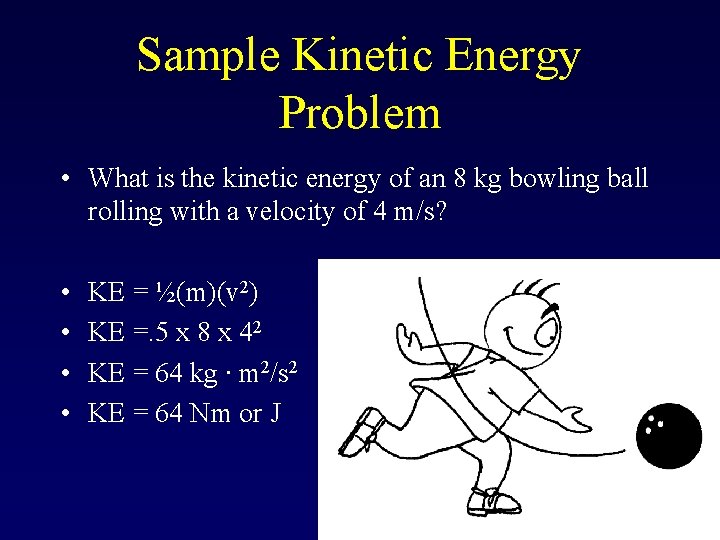
Sample Kinetic Energy Problem • What is the kinetic energy of an 8 kg bowling ball rolling with a velocity of 4 m/s? • • KE = ½(m)(v 2) KE =. 5 x 8 x 42 KE = 64 kg ∙ m 2/s 2 KE = 64 Nm or J

Conservation of Mechanical Energy • Consider a ball tossed vertically into the air Law of conservation of mechanical energy: • When gravity is the only acting external force, a body’s mechanical energy remain constant • (PE + KE) = C – C is a constant indicating the total amount of energy in a system when gravity is the only external force acting on the system – As PE increases, KE decreases and vice-versa

Sample Problem • A 10 kg pumpkin is dropped off a building’s roof from a height of 18 m. What is the velocity immediately before impact with the sidewalk? • PE + KE = C • PE = (wt)(ht) and KE = ½mv 2 • OR… (v 2)2 = (v 1)2 + 2 ad

Principle of Work & Energy • The work of a force is equal to the change in energy that it produces on the object acted on • W = KE + PE + TE TE = Thermal Energy Mechanical work caloric expenditure • ~25% of energy consumed by muscle is converted into work, thus ~75% is thermal energy or used in chemical processes.

Sample Problem • How much mechanical work is required to catch a 0. 7 kg hockey puck shot traveling at a velocity of 45 m/s? • • Δ Δ W = Δ KE = KE 2 – KE 1 KE = ½(mv 2) KE = 0 – (. 5 x. 7 x 452) KE = 708. 75 Nm

Summary • Mechanical work is the product of force and the distance through which the force acts • Mechanical power is the mechanical work done over a time interval • Mechanical energy has two forms: kinetic and potential • When gravity is the only acting external force, the sum of the kinetic and potential energies possessed by a given body remains constant • Changes in a body’s energy are equal to the mechanical work done by an external force