CHAPTER 12 Imperfect Competition 2 The profitmaximizing output

CHAPTER 12 Imperfect Competition

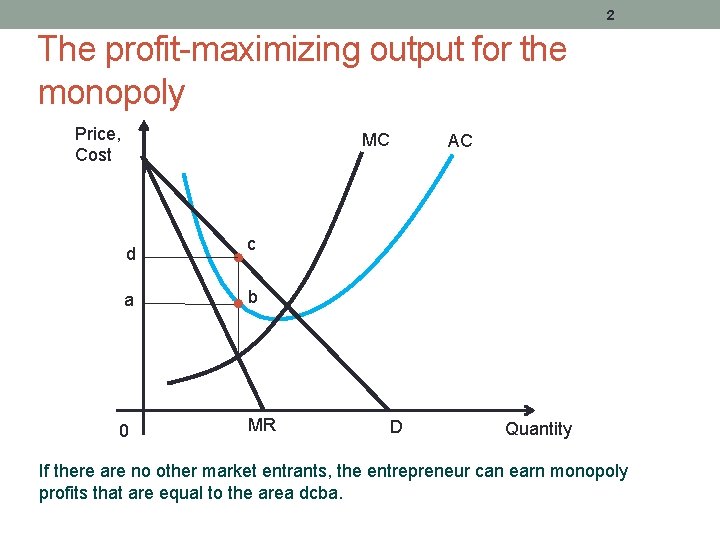
2 The profit-maximizing output for the monopoly Price, Cost MC d AC c a b 0 MR D Quantity If there are no other market entrants, the entrepreneur can earn monopoly profits that are equal to the area dcba.

Chapter Preview • Most markets fall in between perfect competition and monopoly. • An oligopoly is a market with only a few firms, and their behavior is interdependent. • There is no one oligopoly model. In general we want to consider: • Short run: pricing and output decision of the firms. • Long run: advertising, product development. • Very long run: entry and exit.

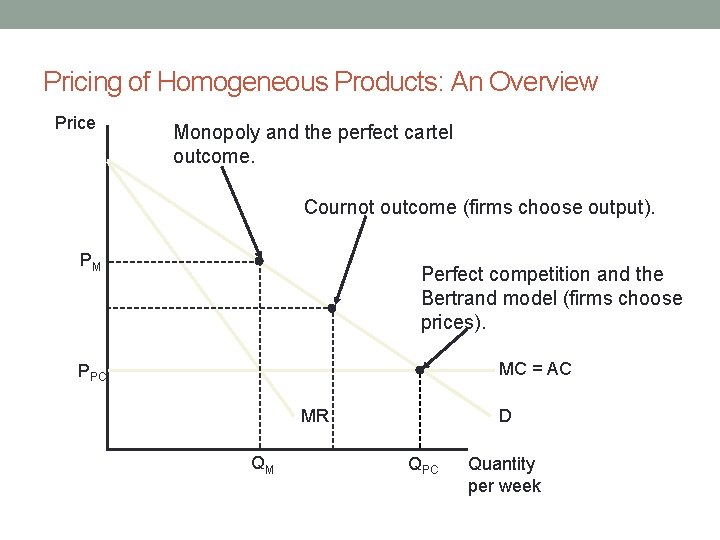
Pricing of Homogeneous Products: An Overview Price Monopoly and the perfect cartel outcome. Cournot outcome (firms choose output). PM Perfect competition and the Bertrand model (firms choose prices). MC = AC PPC D MR QM QPC Quantity per week

Pricing of Homogeneous Products: An Overview • So in an oligopoly there can be a variety of outcomes: • If the firms act as a cartel, get the monopoly solution. • If the firms choose prices simultaneously, get the competitive solution. • If the firms choose output simultaneously get some outcome between perfect competition and monopoly.

6 Cournot Theory of Duopoly & Oligopoly • Cournot model • Two firms • Choose quantity simultaneously • Price - determined on the market • Cournot equilibrium • Nash equilibrium

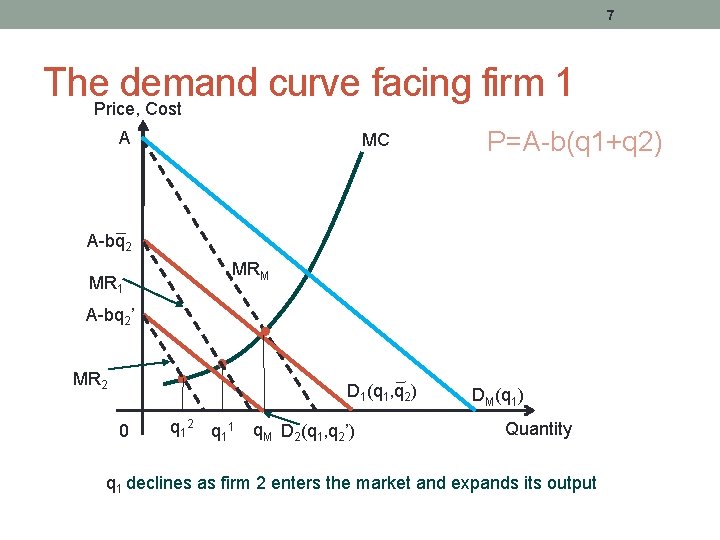
7 The. Price, demand curve facing firm 1 Cost A MC P=A-b(q 1+q 2) A-bq 2 MRM MR 1 A-bq 2’ MR 2 D 1(q 1, q 2) 0 q 1 2 q 1 1 q. M D 2(q 1, q 2’) DM(q 1) Quantity q 1 declines as firm 2 enters the market and expands its output

8 Profit Maximization in a duopoly market • Inverse demand function – linear P=A-b(q 1+q 2) • Maximize profits π1= [A-b(q 1+q 2)]·q 1 - C(q 1) π2= [A-b(q 1+q 2)]·q 2 - C(q 2)

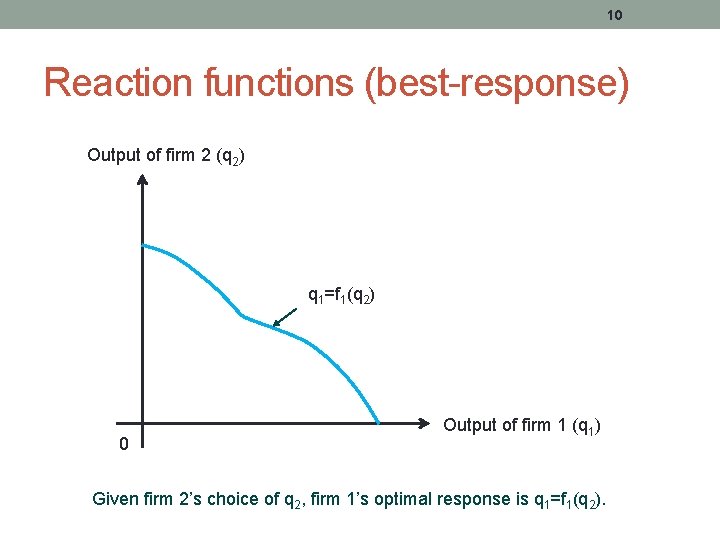
Reaction functions (best-response) • Profit maximization: Set MR=MC • MR now depends on the output of the competing firm • Setting MR 1=MC 1 gives a reaction function for firm 1 • • Gives firm 1’s output as a function of firm 2’s output

10 Reaction functions (best-response) Output of firm 2 (q 2) q 1=f 1(q 2) 0 Output of firm 1 (q 1) Given firm 2’s choice of q 2, firm 1’s optimal response is q 1=f 1(q 2).

11 Reaction Functions • Points on reaction function • Optimal/profit-maximizing choice/output • Of one firm • To a possible output level – other firm • Reaction functions • q 1= f 1(q 2) • q 2 = f 2(q 1)

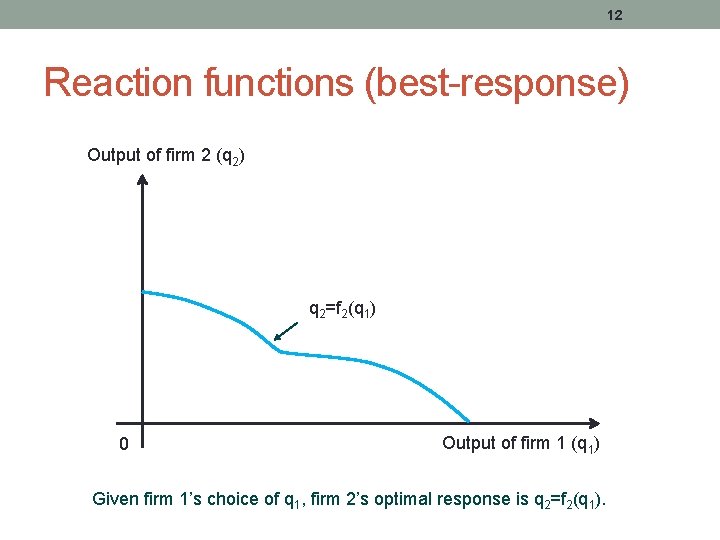
12 Reaction functions (best-response) Output of firm 2 (q 2) q 2=f 2(q 1) 0 Output of firm 1 (q 1) Given firm 1’s choice of q 1, firm 2’s optimal response is q 2=f 2(q 1).

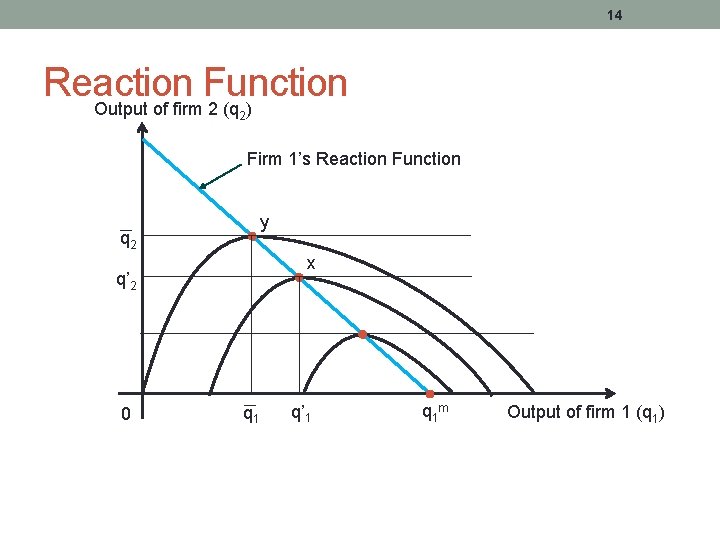
13 Alternative Derivation -Reaction Functions • Isoprofit curves • Combination of q 1 and q 2 that yield same profit • Reaction function (firm 1) • Different output levels – firm 2 • Tangency points – firm 1

14 Reaction Function Output of firm 2 (q ) 2 Firm 1’s Reaction Function y q 2 x q’ 2 0 q 1 q’ 1 q 1 m Output of firm 1 (q 1)

15 Deriving a Cournot Equilibrium • Cournot equilibrium • Intersection of the two Reaction functions • Same graph