Chapter 12 Fourier Transforms of Discrete Signals Sampling

Chapter 12 Fourier Transforms of Discrete Signals

Sampling • Continuous signals are digitized using digital computers • When we sample, we calculate the value of the continuous signal at discrete points – How fast do we sample – What is the value of each point • Quantization determines the value of each samples value

Sampling Periodic Functions - Note that wb = Bandwidth, thus if (signal overlaps) -To avoid aliasing -According sampling theory: then aliasing occurs To hear music up to 20 KHz a CD should sample at the rate of 44. 1 KHz

Discrete Time Fourier Transform • In likely we only have access to finite amount of data sequences (after sampling) • Recall for continuous time Fourier transform, when the signal is sampled: • Assuming • Discrete-Time Fourier Transform (DTFT):

Discrete Time Fourier Transform • Discrete-Time Fourier Transform (DTFT): • A few points – DTFT is periodic in frequency with period of 2 p – X[n] is a discrete signal – DTFT allows us to find the spectrum of the discrete signal as viewed from a window

Example D See map!

Example of Convolution • Convolution – We can write x[n] (a periodic function) as an infinite sum of the function xo[n] (a non-periodic function) shifted N units at a time – This will result – Thus See map!

Finding DTFT For periodic signals • Starting with xo[n] • DTFT of xo[n] Example

Example A & B notes X[n]=a|n|, 0 < a < 1. notes

DT Fourier Transforms 1. 2. 3. W is in radian and it is between 0 and 2 p in each discrete time interval This is different from w where it was between – INF and + INF Note that X(W) is periodic

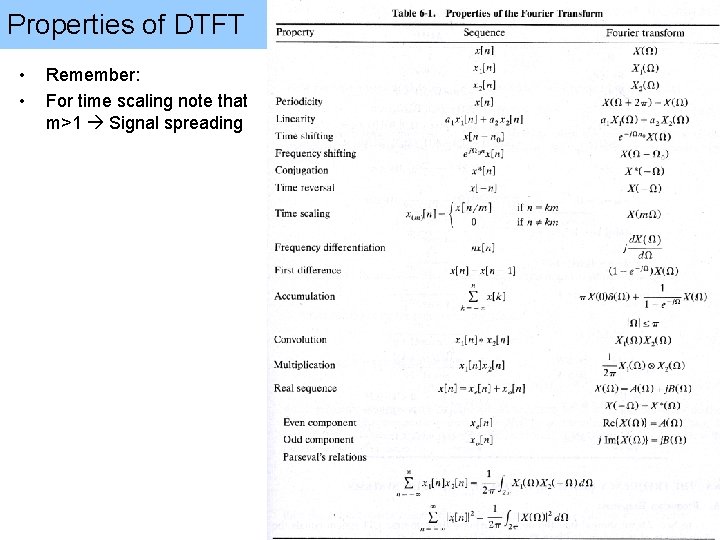
Properties of DTFT • • Remember: For time scaling note that m>1 Signal spreading

Fourier Transform of Periodic Sequences • Check the map~~~~~ See map!

Discrete Fourier Transform • We often do not have an infinite amount of data which is required by DTFT – For example in a computer we cannot calculate uncountable infinite (continuum) of frequencies as required by DTFT • Thus, we use DTF to look at finite segment of data – We only observe the data through a window – In this case the xo[n] is just a sampled data between n=0, n=N-1 (N points)

Discrete Fourier Transform • It turns out that DFT can be defined as • Note that in this case the points are spaced 2 pi/N; thus the resolution of the samples of the frequency spectrum is 2 pi/N. • We can think of DFT as one period of discrete Fourier series

A short hand notation remember:

Inverse of DFT • We can obtain the inverse of DFT • Note that

Using MATLAB to Calculate DFT • Example: – – or Assume N=4 x[n]=[1, 2, 3, 4] n=0, …, 3 Find X[k]; k=0, …, 3

Example of DFT • Find X[k] – We know k=1, . . , 7; N=8

Example of DFT

Example of DFT Polar plot for Time shift Property of DFT Other DFT properties: http: //cnx. org/content/m 12019/latest/

Example of DFT

Example of DFT Summation for X[k] Using the shift property!

Example of IDFT Remember:

Example of IDFT Remember:

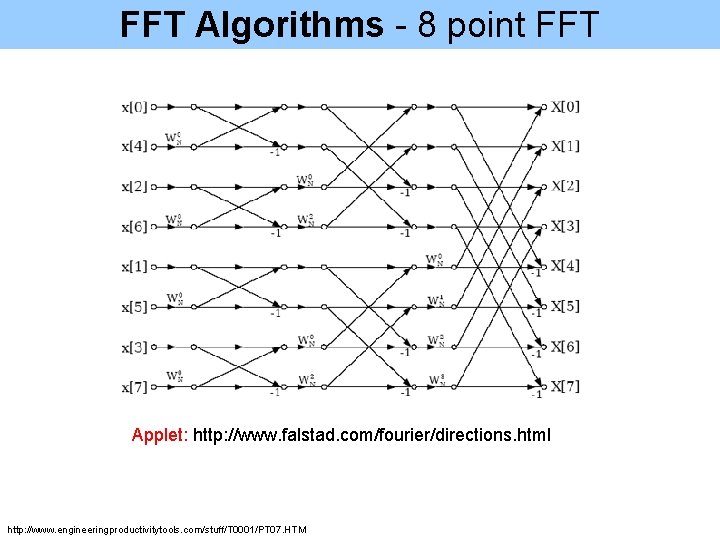
Fast Fourier Transform Algorithms • Consider DTFT • Basic idea is to split the sum into 2 subsequences of length N/2 and continue all the way down until you have N/2 subsequences of length 2 Log 2(8) N

Radix-2 FFT Algorithms - Two point FFT • We assume N=2^m – This is called Radix-2 FFT Algorithms • Let’s take a simple example where only two points are given n=0, n=1; N=2 Butterfly FFT y 0 Advantage: Less computationally intensive: N/2. log(N) http: //www. cmlab. csie. ntu. edu. tw/cml/dsp/training/coding/transform/fft. html y 1

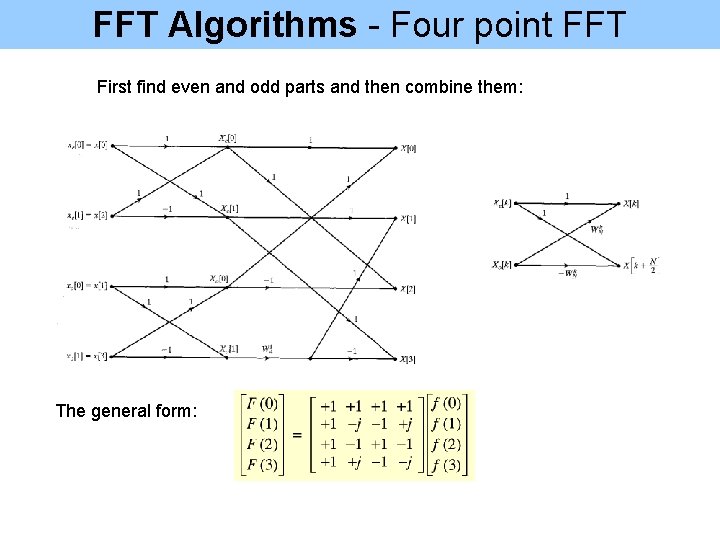
General FFT Algorithm • First break x[n] into even and odd • • Let n=2 m for even and n=2 m+1 for odd Even and odd parts are both DFT of a N/2 point sequence • Break up the size N/2 subsequent in half by letting 2 m m The first subsequence here is the term x[0], x[4], … The second subsequent is x[2], x[6], … • •

Example Let’s take a simple example where only two points are given n=0, n=1; N=2 Same result

FFT Algorithms - Four point FFT First find even and odd parts and then combine them: The general form:

FFT Algorithms - 8 point FFT Applet: http: //www. falstad. com/fourier/directions. html http: //www. engineeringproductivitytools. com/stuff/T 0001/PT 07. HTM

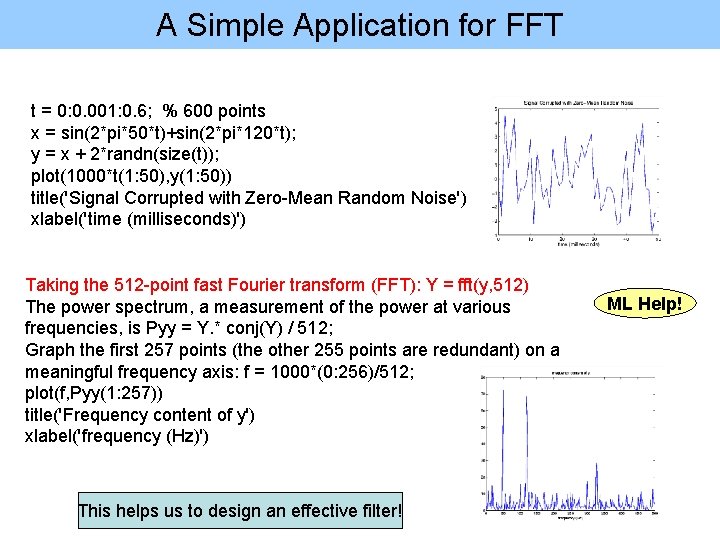
A Simple Application for FFT t = 0: 0. 001: 0. 6; % 600 points x = sin(2*pi*50*t)+sin(2*pi*120*t); y = x + 2*randn(size(t)); plot(1000*t(1: 50), y(1: 50)) title('Signal Corrupted with Zero-Mean Random Noise') xlabel('time (milliseconds)') Taking the 512 -point fast Fourier transform (FFT): Y = fft(y, 512) The power spectrum, a measurement of the power at various frequencies, is Pyy = Y. * conj(Y) / 512; Graph the first 257 points (the other 255 points are redundant) on a meaningful frequency axis: f = 1000*(0: 256)/512; plot(f, Pyy(1: 257)) title('Frequency content of y') xlabel('frequency (Hz)') This helps us to design an effective filter! ML Help!

Example • Express the DFT of the 9 -point {x[0], …, x[9]} in terms of the DFTs of 3 -point sequences {x[0], x[3], x[6]}, {x[1], x[4], x[7]}, and {x[2], x[5], x[8]}. Later

References • Read Schaum’s Outlines: Chapter 6 • Do Chapter 12 problems: 19, 20, 26, 5, 7