Chapter 12 Congruence and Similarity with Constructions Copyright




















- Slides: 27

Chapter 12 Congruence and Similarity with Constructions Copyright © 2016, 2013, and 2010, Pearson Education, Inc.

12 -1 Congruence Through Constructions Students will be able to understand explain • Geometric construction leasing to the SSS, SAS, and HL congruence properties. • Isosceles triangle properties. • Altitudes and perpendicular bisectors. • Circles circumscribing triangles and quadrilaterals. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 2

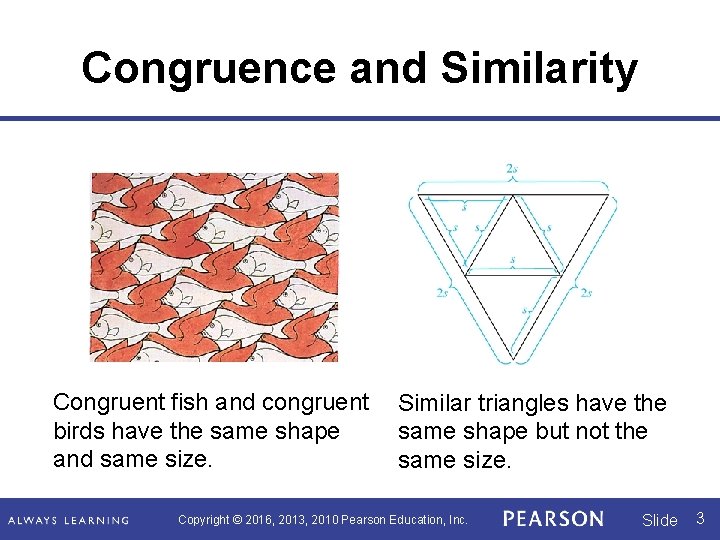
Congruence and Similarity Congruent fish and congruent birds have the same shape and same size. Similar triangles have the same shape but not the same size. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 3

Congruence and Similarity Similar objects ( ) have the same shape but not necessarily the same size. Congruent objects ( ) have the same shape and the same size. Congruent objects are similar, but similar objects are not necessarily congruent. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 4

Definition Congruent Segments and Angles Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 5

Geometric Constructions 1. Given two points, a unique straight line can be drawn containing the points as well as a unique segment connecting the points. 2. A circle can be drawn given its center and radius. 3. Any number of points can be chosen on a given line, segment, or circle. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 6

Geometric Constructions 4. Points of intersection of two lines, two circles, or a line and a circle can be used to construct segments, lines, or circles. 5. No other instruments (such as a marked ruler, triangle, or protractor) or procedures can be used to perform Euclidean constructions. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 7

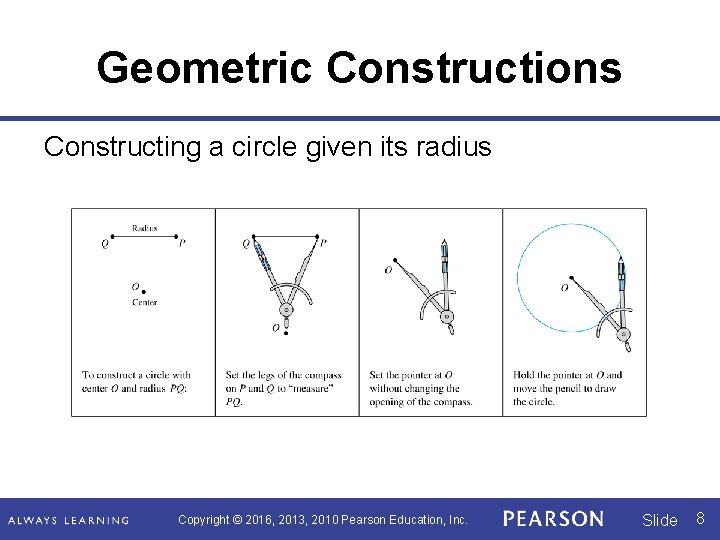
Geometric Constructions Constructing a circle given its radius Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 8

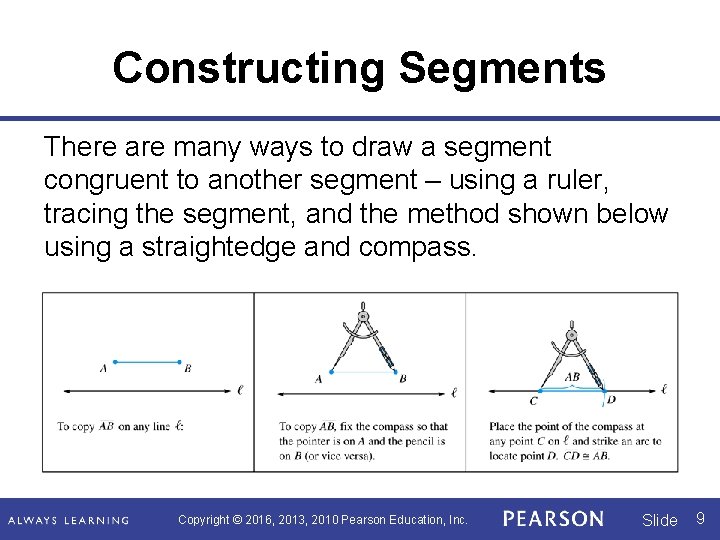
Constructing Segments There are many ways to draw a segment congruent to another segment – using a ruler, tracing the segment, and the method shown below using a straightedge and compass. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 9

Triangle Congruence Two figures are congruent if it is possible to fit one figure onto the other so that matching parts coincide. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 10

Definition Congruent Triangles Corresponding parts of congruent triangles are congruent, abbreviated CPCTC. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 11

Example Write an appropriate symbolic congruence for each of the pairs. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 12

Side, Side Congruence Condition (SSS) If the three sides of one triangle are congruent, respectively, to the three sides of a second triangle, then the triangles are congruent. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 13

Example Use SSS to explain why the given triangles are congruent. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 14

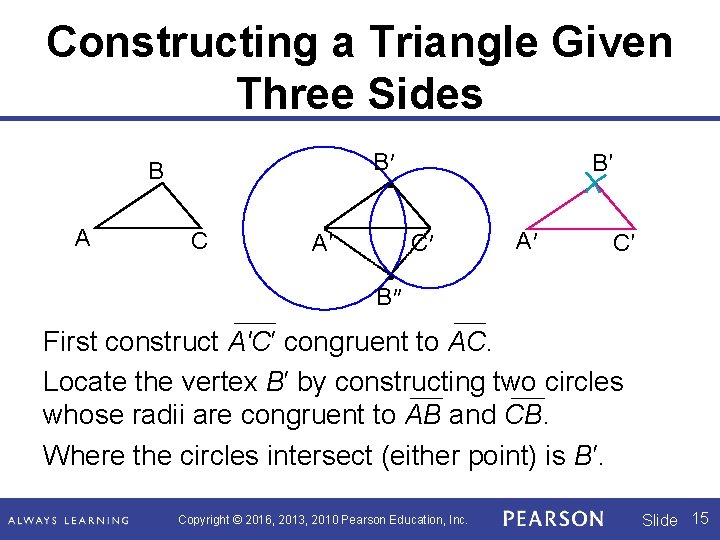
Constructing a Triangle Given Three Sides B′ B A C A′ B′ C′ A′ C′ B″ First construct A′C′ congruent to AC. Locate the vertex B′ by constructing two circles whose radii are congruent to AB and CB. Where the circles intersect (either point) is B′. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 15

Triangle Inequality The sum of the measures of any two sides of a triangle must be greater than the measure of the third side. E. g. , 5”, 6”, and 8” 3 cm, 4 cm, and 5 cm 2. 5 m, 7. 2 m, and 8. 6 m Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 16

Constructing Congruent Angles With the compass and straightedge alone, it is impossible in general to construct an angle if given only its measure. Instead, a protractor or a geometry drawing utility or some other measuring tool must be used. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 17

Side, Angle, Side Congruence (SAS) If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, respectively, then the two triangles are congruent. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 18

Constructions Involving Two Sides and an Included Angle of a Triangle First draw a ray with endpoint A′, and then construct A′C′ congruent to AC. Then construct Mark B′ on the side of not containing C′ so that Then connect B′ and C′ to complete the triangle. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 19

Example Use SAS to show that the given pair of triangles are congruent. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 20

Hypotenuse-Leg Theorem If the hypotenuse and a leg of one right triangle are congruent to the hypotenuse and a leg of another right triangle, then the triangles are congruent. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 21

Selected Triangle Properties Any point equidistant from the endpoints of a segment is on the perpendicular bisector of the segment. Any point on the perpendicular bisector of a segment is equidistant from the endpoints of the segment. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 22

Selected Triangle Properties For every isosceles triangle: The angles opposite the congruent sides are congruent. (Base angles of an isosceles triangle are congruent). The angle bisector of an angle formed by two congruent sides contains an altitude of the triangle and is the perpendicular bisector of the third side of the triangle. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 23

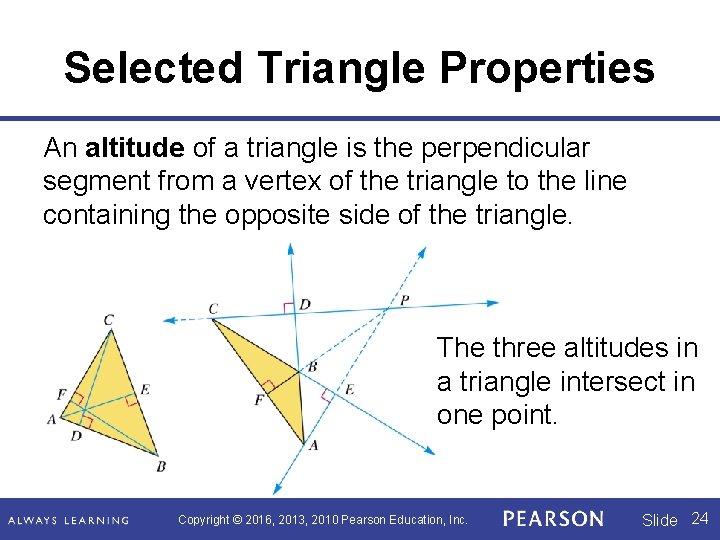
Selected Triangle Properties An altitude of a triangle is the perpendicular segment from a vertex of the triangle to the line containing the opposite side of the triangle. The three altitudes in a triangle intersect in one point. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 24

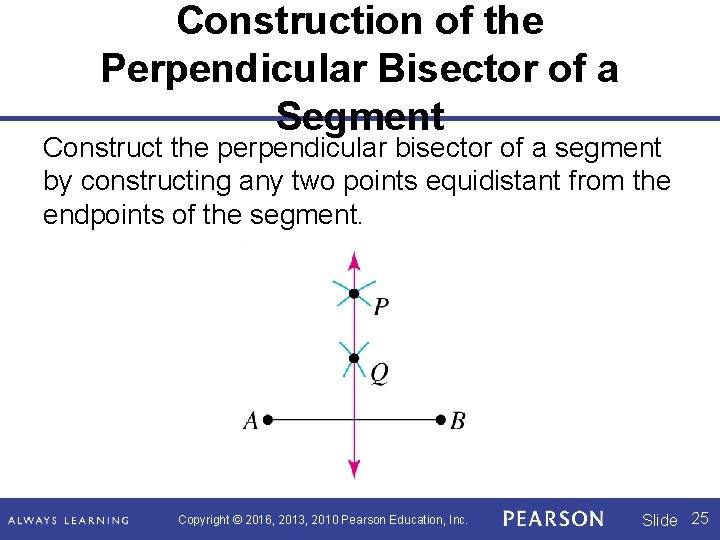
Construction of the Perpendicular Bisector of a Segment Construct the perpendicular bisector of a segment by constructing any two points equidistant from the endpoints of the segment. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 25

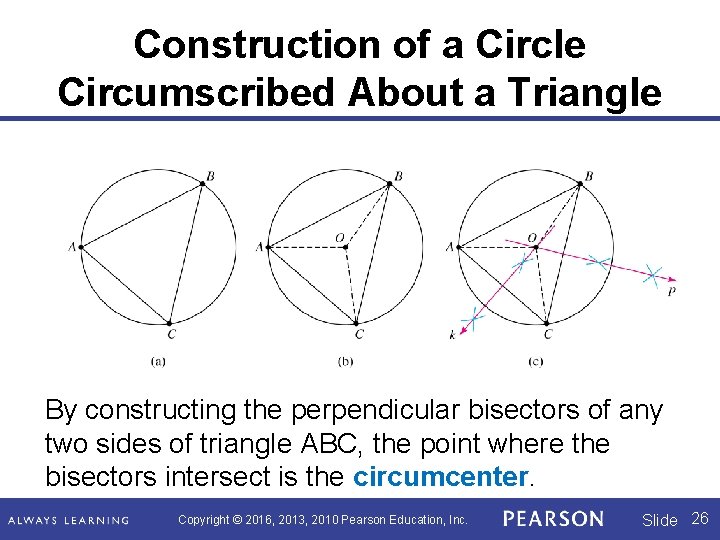
Construction of a Circle Circumscribed About a Triangle By constructing the perpendicular bisectors of any two sides of triangle ABC, the point where the bisectors intersect is the circumcenter. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 26

Circles Circumscribed About Some Quadrilaterals If a circle can be circumscribed about a convex quadrilateral, then the sum of the measures of a pair of opposite angles of the quadrilateral is 180º; that is, the angles are supplementary. Conversely, If the sum of the measures of a pair of opposite angles of a convex quadrilateral is 180º (that is the angles are supplementary), then a circle can be circumscribed about the quadrilateral. Copyright © 2016, 2013, 2010 Pearson Education, Inc. Slide 27