Chapter 12 Beam Behavior Bending Shear and Deflection

Chapter 12 Beam Behavior – Bending, Shear, and Deflection

Behavior of a Beam in Bending • When a beam is subjected to vertical forces it responds by physically deflecting under that load • When the same beam is supported at two ends and a load is placed upon that beam, then the beam reacts by compressing along the top side of the beams and stretching along the bottom

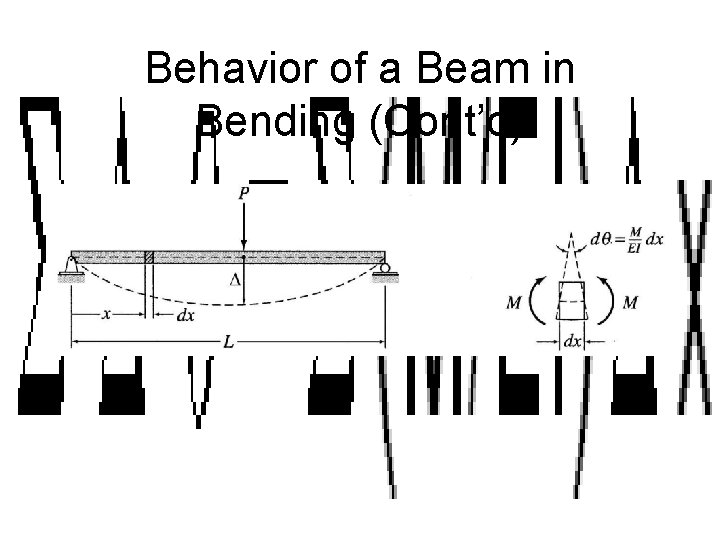
Behavior of a Beam in Bending (Cont’d)

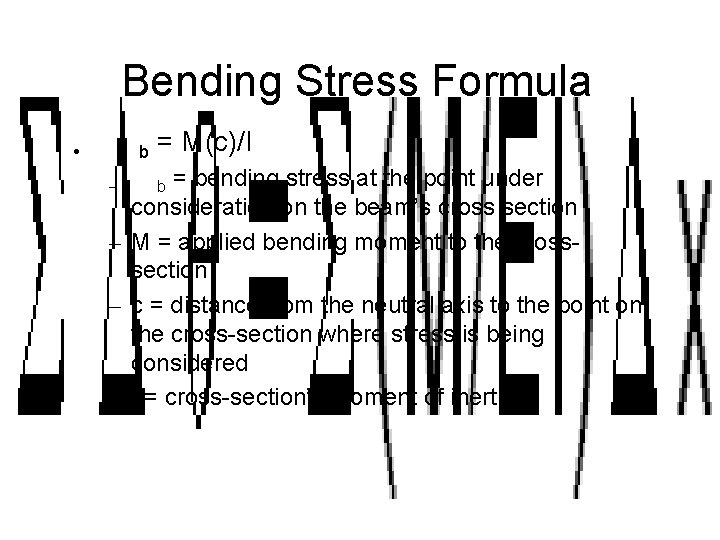
Bending Stress Formula b • = M(c)/I = bending stress at the point under consideration on the beam’s cross section – M = applied bending moment to the crosssection – c = distance from the neutral axis to the point on the cross-section where stress is being considered – I = cross-section’s moment of inertia – b

Shear Stresses in Beams • Shear stresses that developed vertically on a beam element must likewise develop on perpendicular planes such that equilibrium is maintained

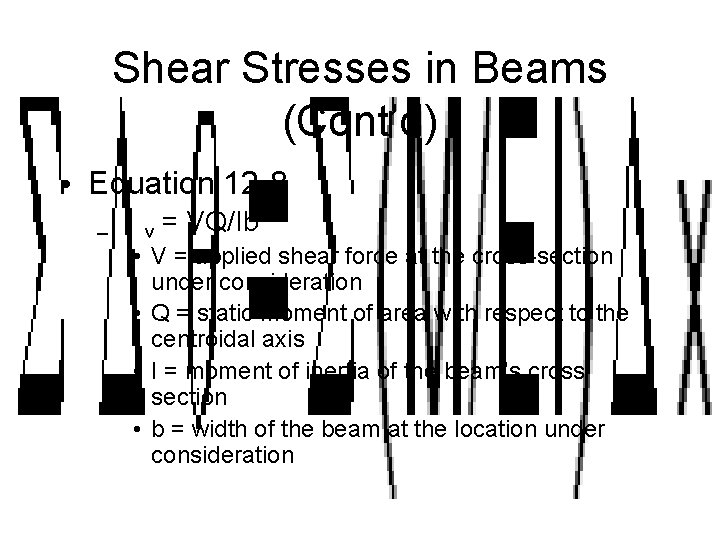
Shear Stresses in Beams (Cont’d) • Equation 12 -8 – v = VQ/Ib • V = applied shear force at the cross-section under consideration • Q = static moment of area with respect to the centroidal axis • I = moment of inertia of the beam’s cross section • b = width of the beam at the location under consideration

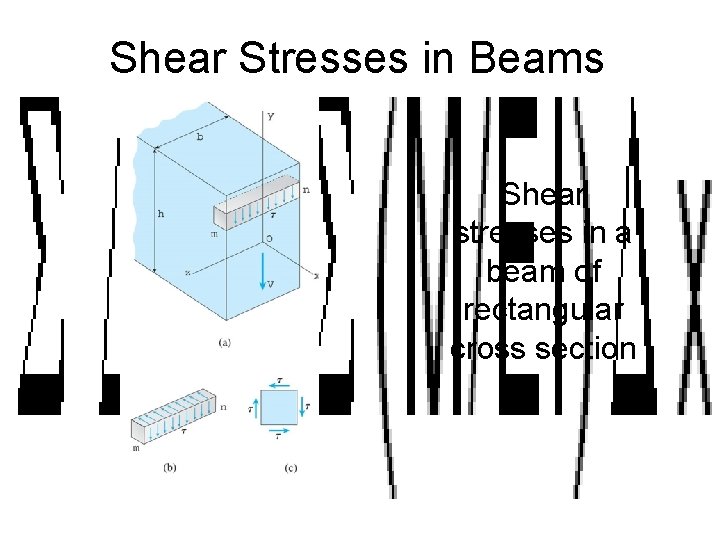
Shear Stresses in Beams Shear stresses in a beam of rectangular cross section

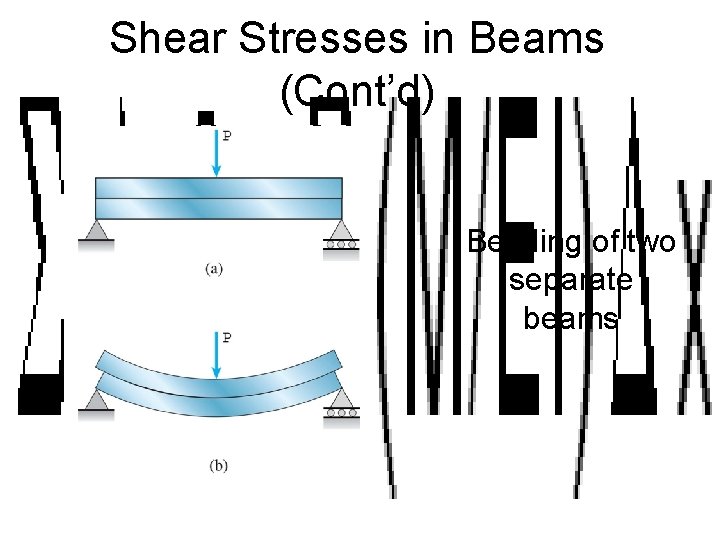
Shear Stresses in Beams (Cont’d) Bending of two separate beams

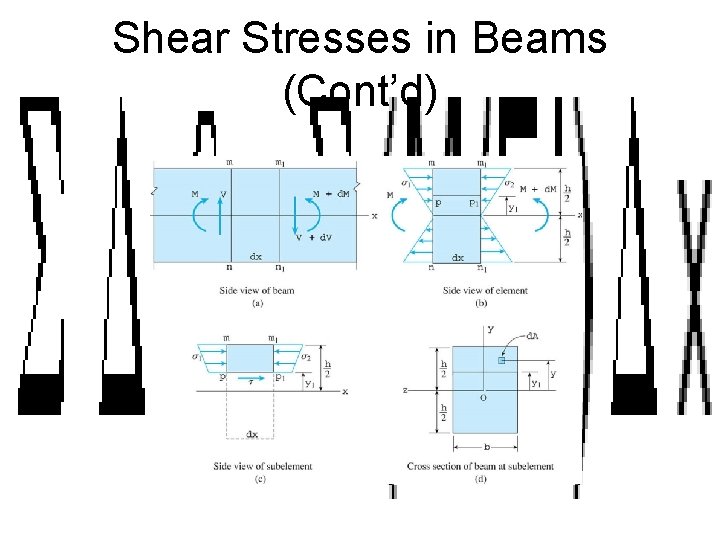
Shear Stresses in Beams (Cont’d)

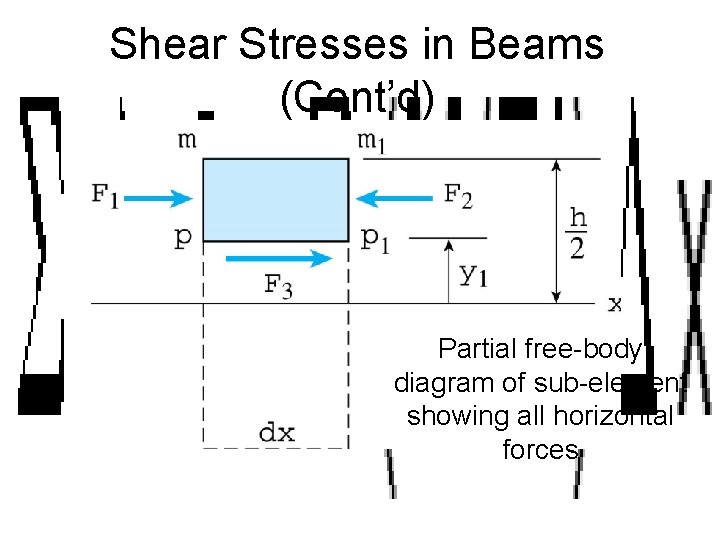
Shear Stresses in Beams (Cont’d) Partial free-body diagram of sub-element showing all horizontal forces

Shear Stresses in Beams (Cont’d) Distribution of shear stresses in a beam of rectangular cross section: (a) cross section of beam, and (b) diagram showing the parabolic distribution of shear stresses over the height of the beam

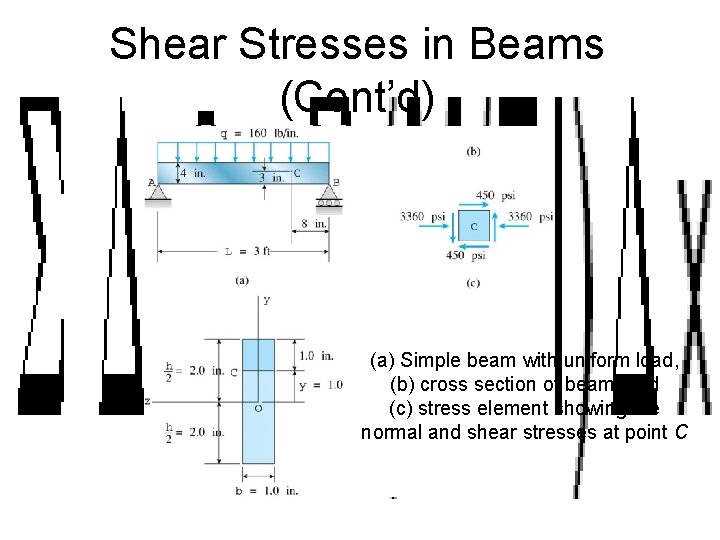
Shear Stresses in Beams (Cont’d) (a) Simple beam with uniform load, (b) cross section of beam, and (c) stress element showing the normal and shear stresses at point C

The Mechanics of Deflection

The Mechanics of Deflection (Cont’d)

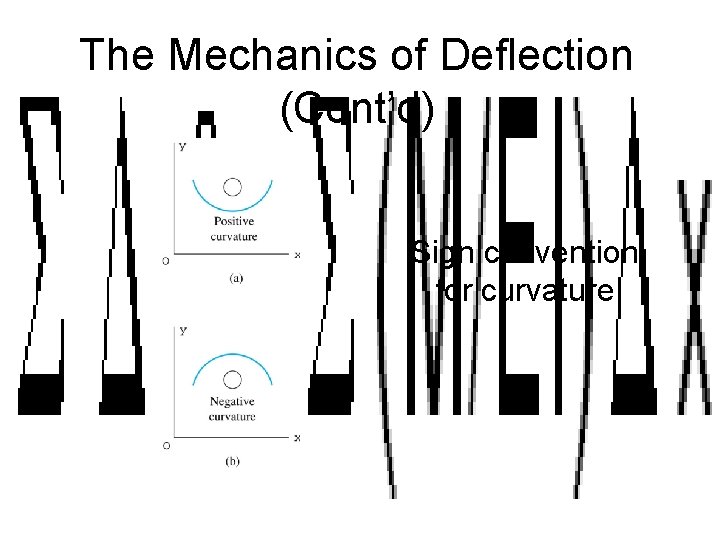
The Mechanics of Deflection (Cont’d) Sign convention for curvature

The Moment-Area Method • The most common method of calculating the deflection at any point along a beam • Equation 12 -14 –

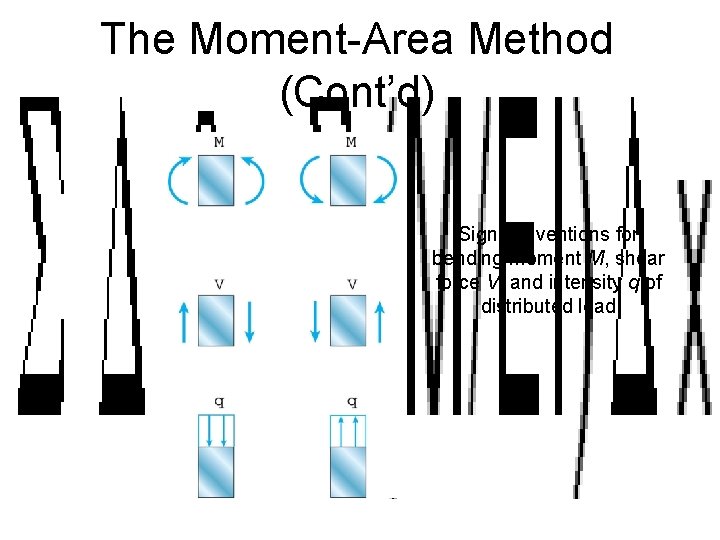
The Moment-Area Method (Cont’d) Sign conventions for bending moment M, shear force V, and intensity q of distributed load

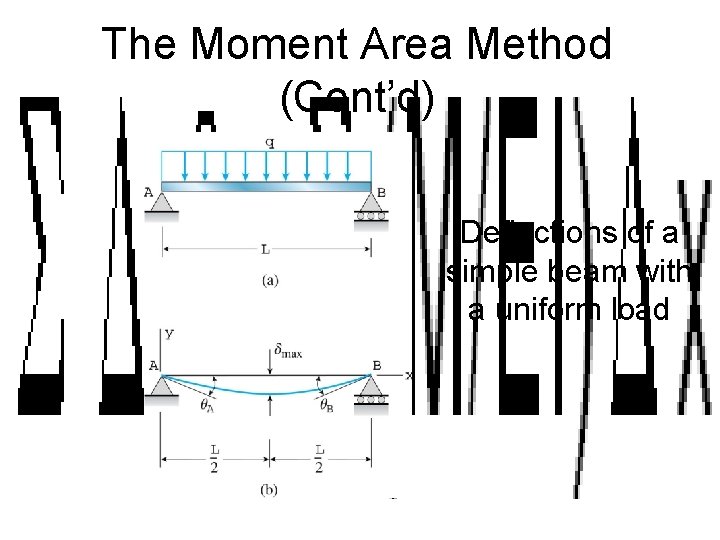
The Moment Area Method (Cont’d) Deflections of a simple beam with a uniform load

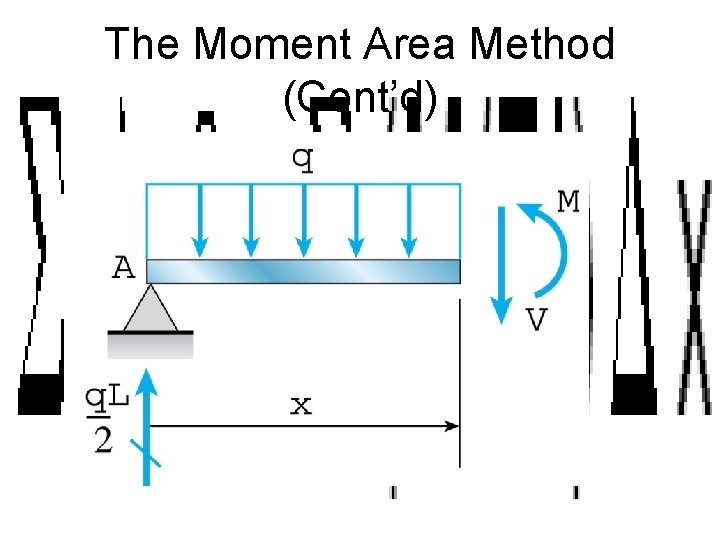
The Moment Area Method (Cont’d)

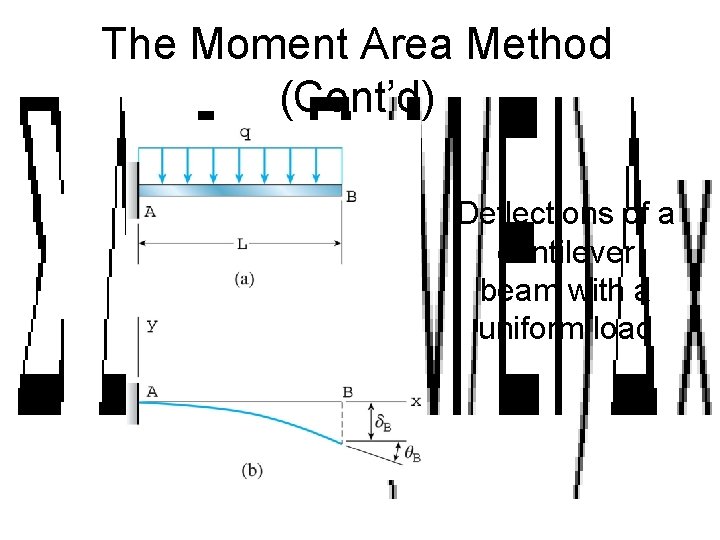
The Moment Area Method (Cont’d) Deflections of a cantilever beam with a uniform load

The Moment Area Method (Cont’d)

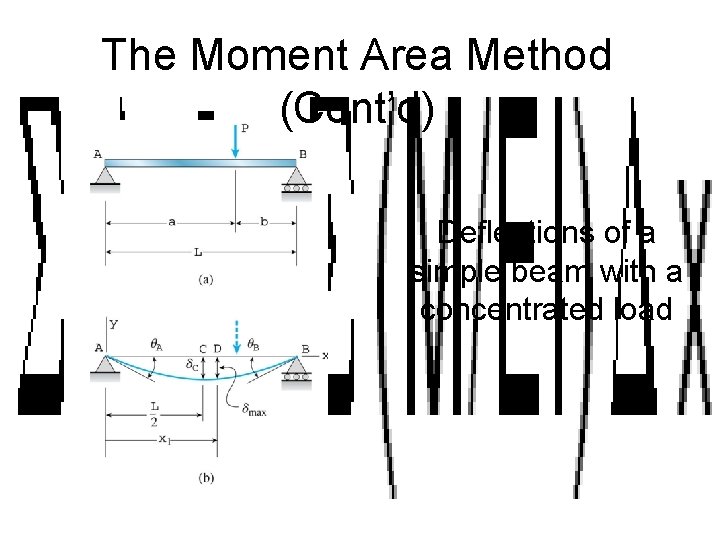
The Moment Area Method (Cont’d) Deflections of a simple beam with a concentrated load

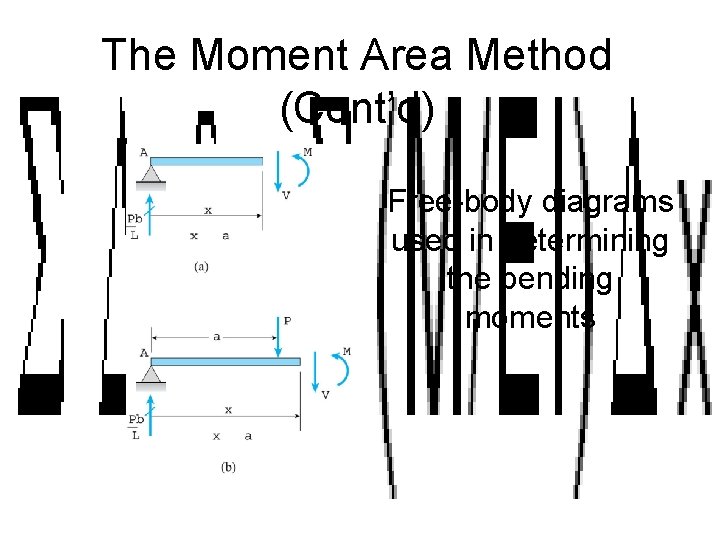
The Moment Area Method (Cont’d) Free-body diagrams used in determining the bending moments

The Moment Area Method (Cont’d) Deflections of a cantilever beam with a triangular load

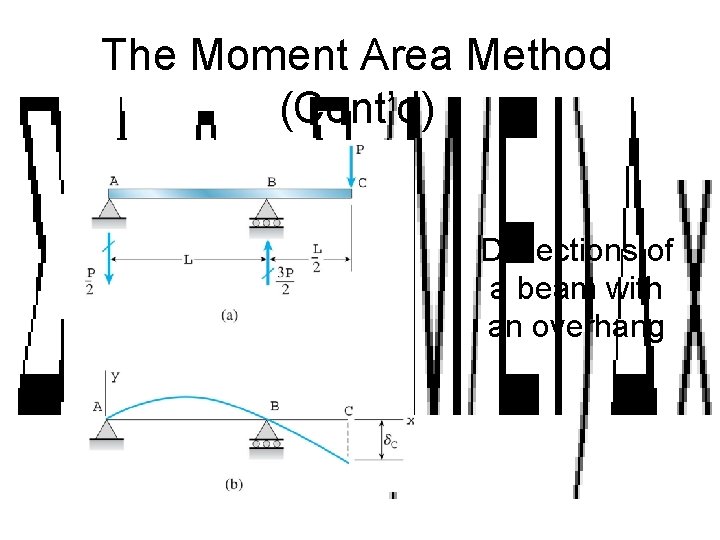
The Moment Area Method (Cont’d) Deflections of a beam with an overhang

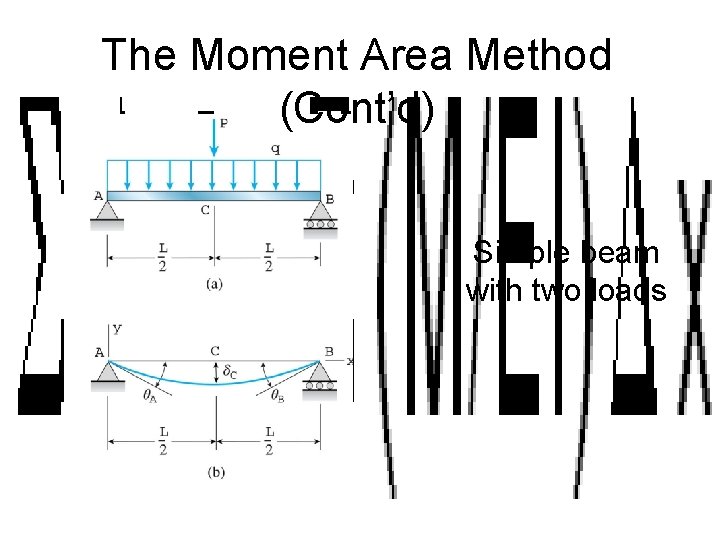
The Moment Area Method (Cont’d) Simple beam with two loads

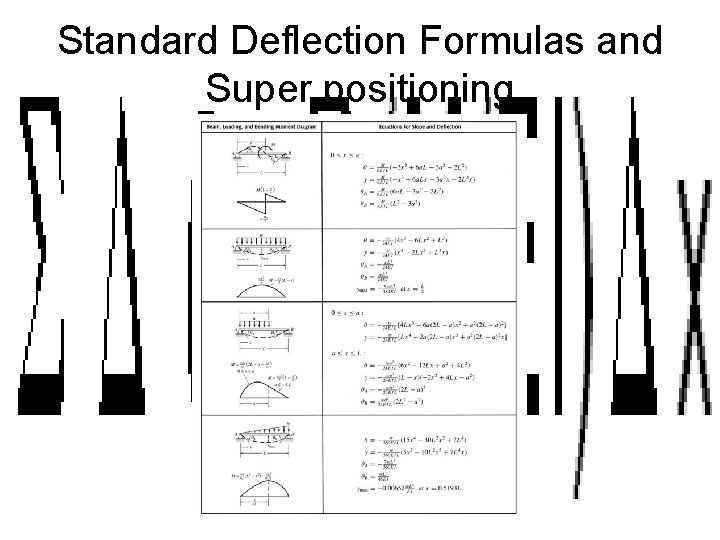
Standard Deflection Formulas and Super positioning

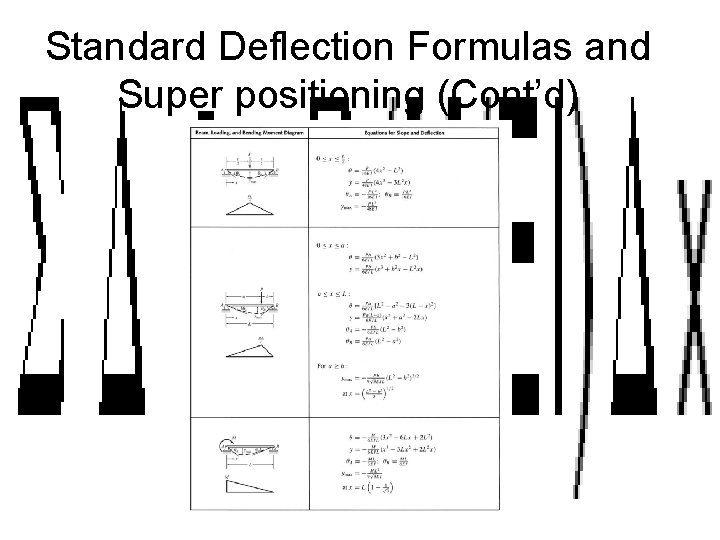
Standard Deflection Formulas and Super positioning (Cont’d)

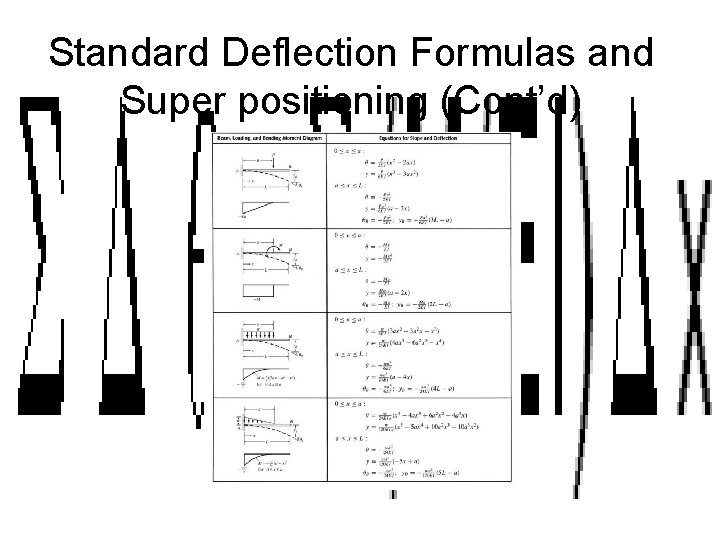
Standard Deflection Formulas and Super positioning (Cont’d)

Deflection Strength Failure: Ponding • The retention of water on a flat or semiflat roof during periods of heavy rainfall or snow melt