Chapter 12 Angle Properties of a Circle Recall

  • Slides: 19
Download presentation
Chapter 12 Angle Properties of a Circle

Chapter 12 Angle Properties of a Circle

Recall n Major Arc AB n Major sector O is the centre of circle

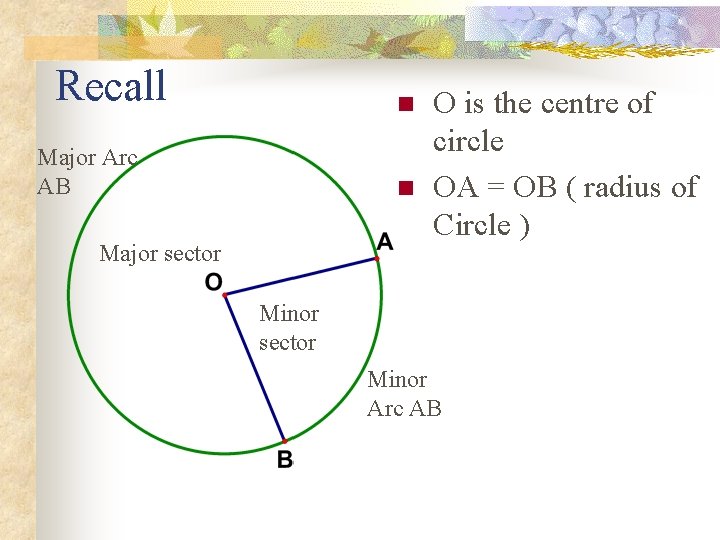
Recall n Major Arc AB n Major sector O is the centre of circle OA = OB ( radius of Circle ) Minor sector Minor Arc AB

Recall diameter chord Centre tangent Tangent is perpendicular to the diameter

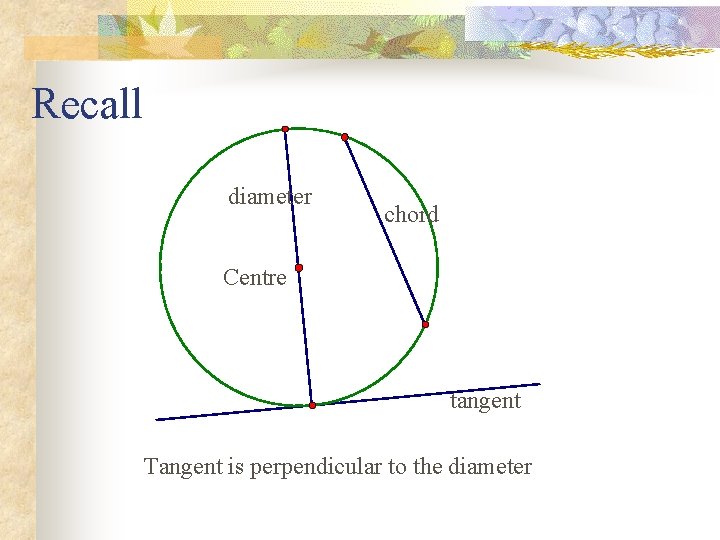
Recall diameter chord Centre tangent Tangent is perpendicular to the diameter

Recall • If AC = BC • then OCA = OCB = 90 •

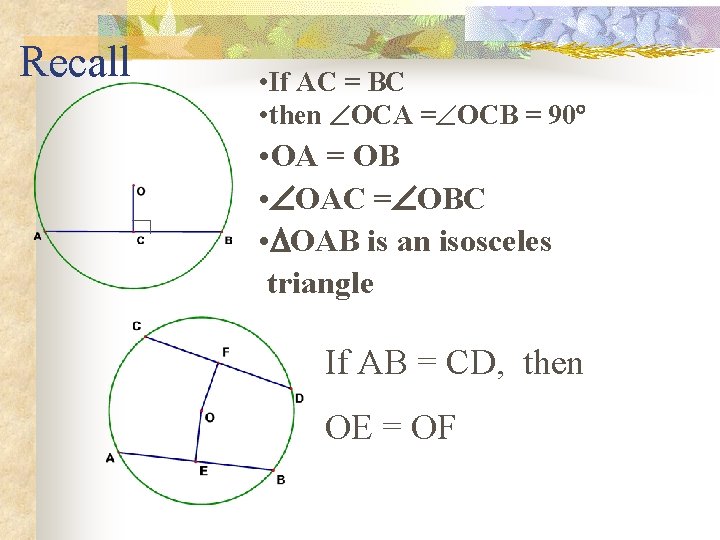
Recall • If AC = BC • then OCA = OCB = 90 • OA = OB • OAC = OBC • OAB is an isosceles triangle If AB = CD, then OE = OF

Recall A B O j C • OA = OC (radius) • AB and

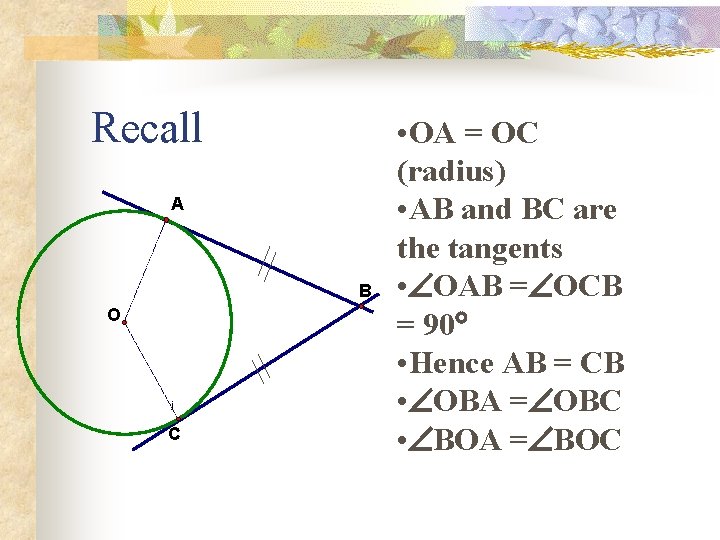
Recall A B O j C • OA = OC (radius) • AB and BC are the tangents • OAB = OCB = 90 • Hence AB = CB • OBA = OBC • BOA = BOC

Introduction Major Segment Minor Segment Chord AB • The segment bounded by the arc

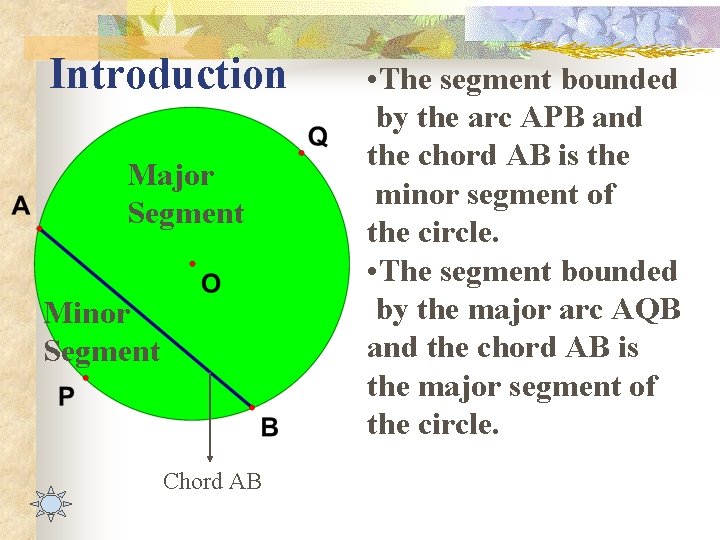
Introduction Major Segment Minor Segment Chord AB • The segment bounded by the arc APB and the chord AB is the minor segment of the circle. • The segment bounded by the major arc AQB and the chord AB is the major segment of the circle.

Angle at the circumference ACB is subtended by the minor arc AB at the

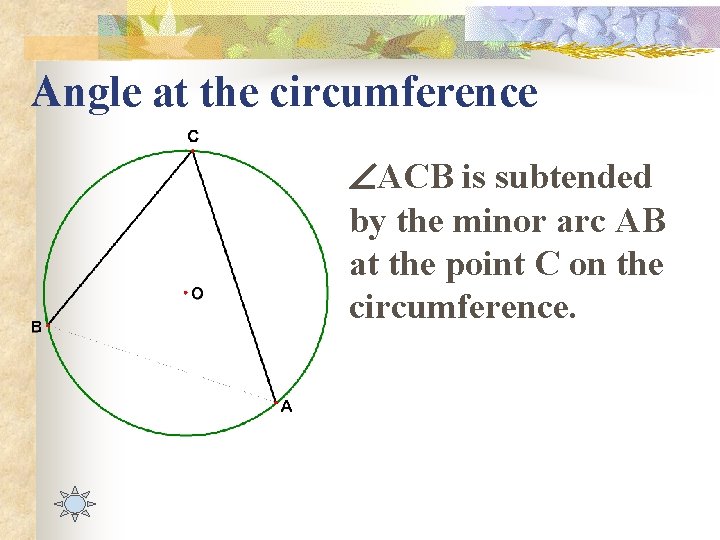
Angle at the circumference ACB is subtended by the minor arc AB at the point C on the circumference.

Angle at the centre n n AOB is the angle at the centre. Reflex

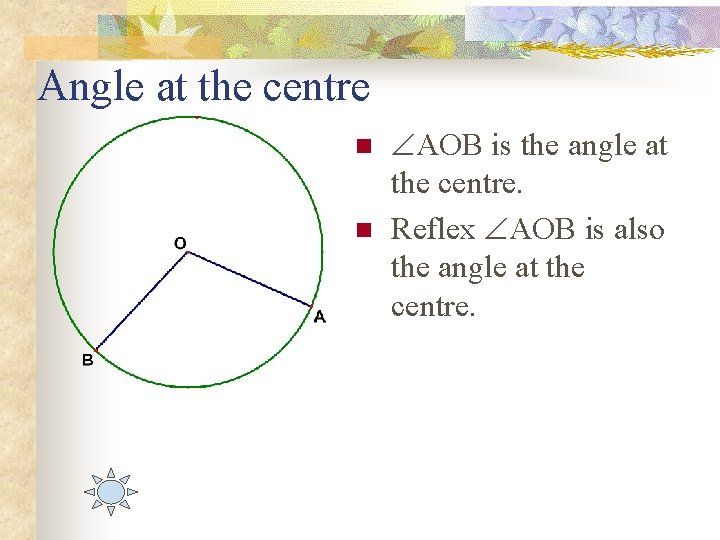
Angle at the centre n n AOB is the angle at the centre. Reflex AOB is also the angle at the centre.

Time to work n n n Skill Practice 12 A Page 109 Q 1

Time to work n n n Skill Practice 12 A Page 109 Q 1 a to e

Angles at the same segment n n APB = AQB Angles in the same

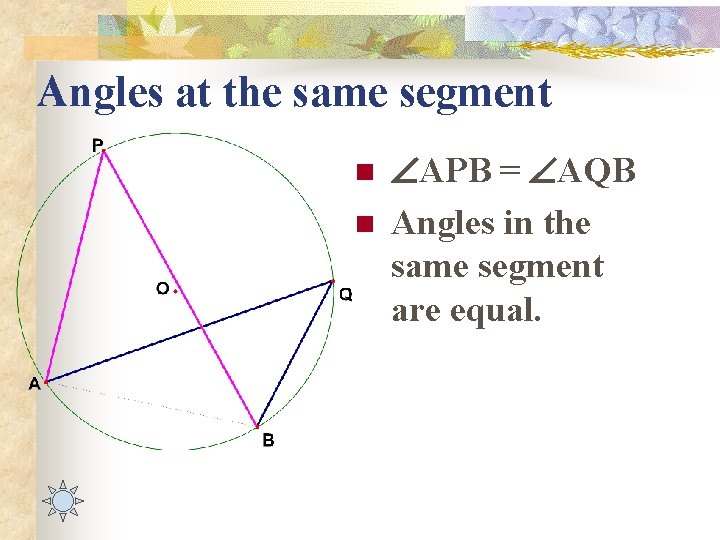
Angles at the same segment n n APB = AQB Angles in the same segment are equal.

Relationship between Angle at centre and angle at circumference n n n The angle

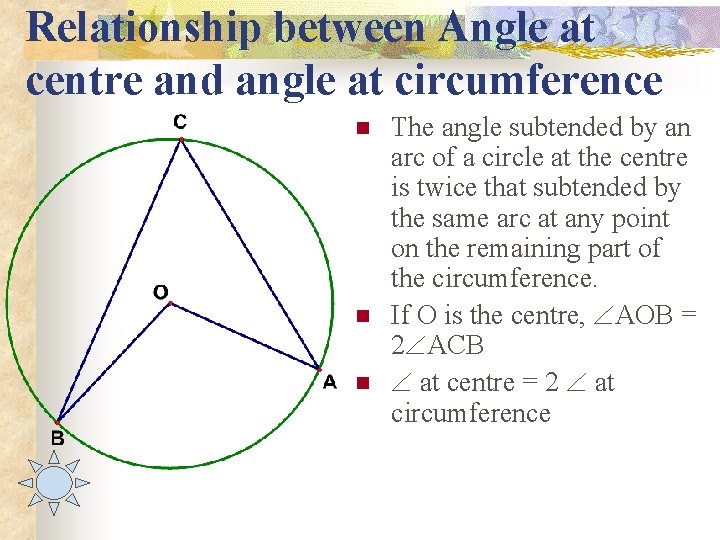
Relationship between Angle at centre and angle at circumference n n n The angle subtended by an arc of a circle at the centre is twice that subtended by the same arc at any point on the remaining part of the circumference. If O is the centre, AOB = 2 ACB at centre = 2 at circumference

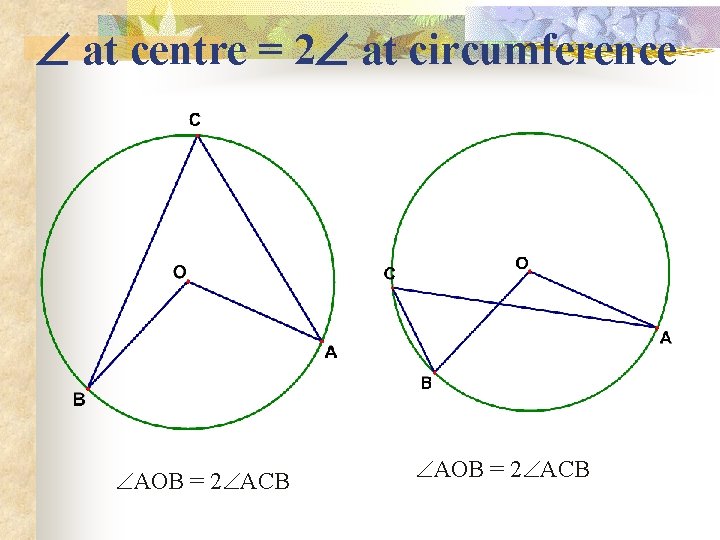
at centre = 2 at circumference AOB = 2 ACB

at centre = 2 at circumference AOB = 2 ACB

at centre = 2 at circumference reflex AOB = 2 ACB

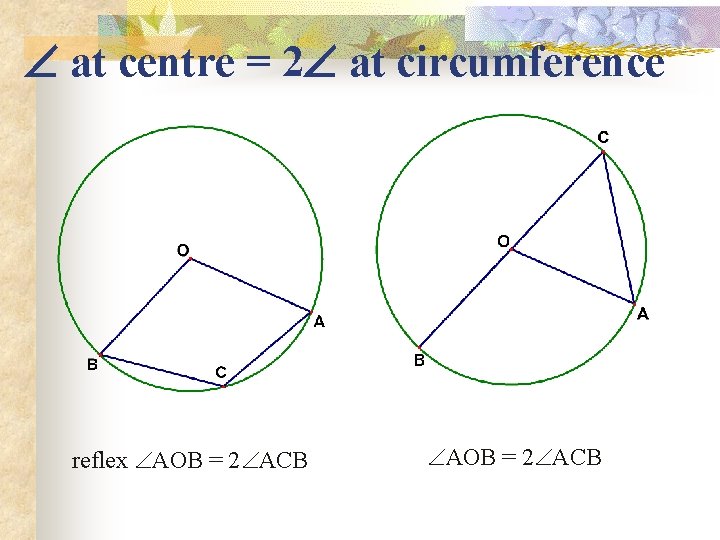
at centre = 2 at circumference reflex AOB = 2 ACB

Time to work n n n Classwork SP 12 A Pg 110 Q 2

Time to work n n n Classwork SP 12 A Pg 110 Q 2 b, d, f Q 3 a, c, e Q 4 a, b n n Homework SP 12 A Pg 110 Q 2 a, c, e Q 3 b, d, f

Angle in a semicircle n n n The angle in a semicircle is a

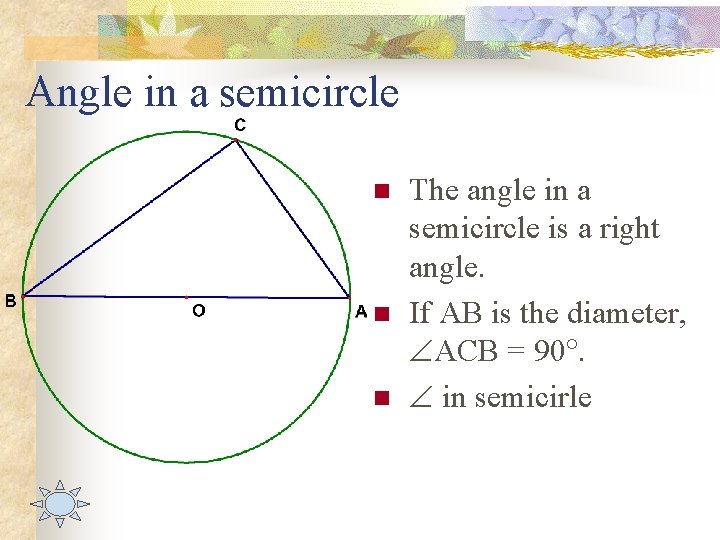
Angle in a semicircle n n n The angle in a semicircle is a right angle. If AB is the diameter, ACB = 90. in semicirle

Angles in opposite segments n n n Angle in opposite segments are supplementary. ABC

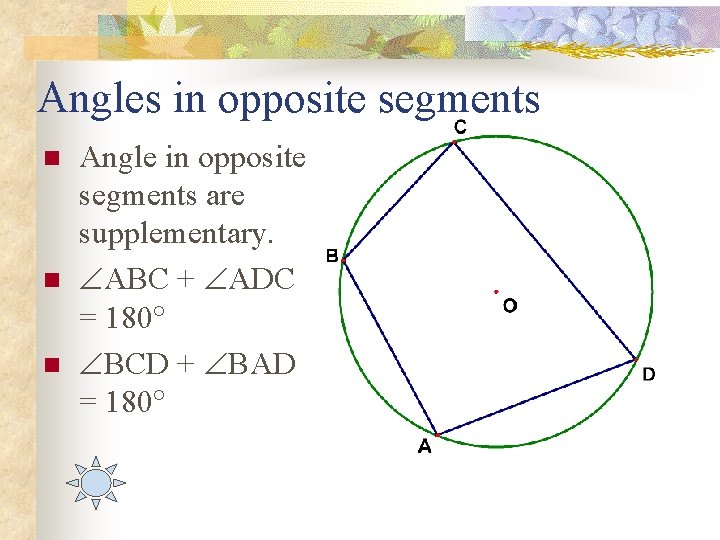
Angles in opposite segments n n n Angle in opposite segments are supplementary. ABC + ADC = 180 BCD + BAD = 180

Exterior angle of a cyclic quadrilateral n C B n O n D A

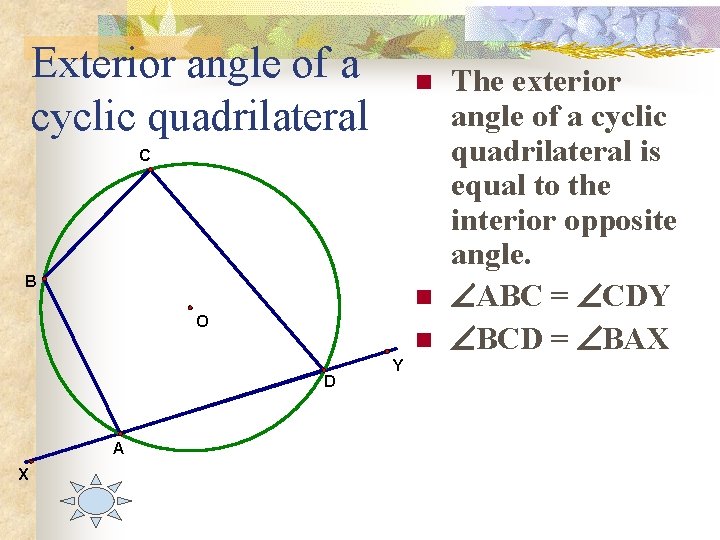
Exterior angle of a cyclic quadrilateral n C B n O n D A X Y The exterior angle of a cyclic quadrilateral is equal to the interior opposite angle. ABC = CDY BCD = BAX

Angle in the alternate segment n n B C n S A T n

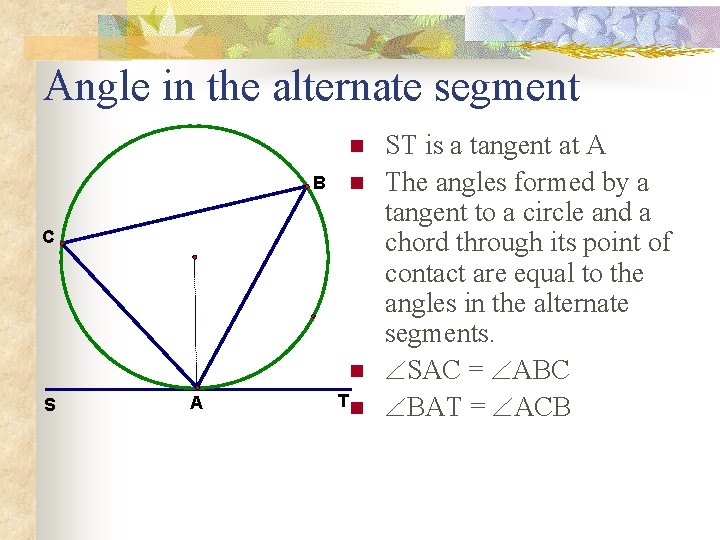
Angle in the alternate segment n n B C n S A T n ST is a tangent at A The angles formed by a tangent to a circle and a chord through its point of contact are equal to the angles in the alternate segments. SAC = ABC BAT = ACB

Time to work n n n n Classwork SP 12 B Pg 113 Q

Time to work n n n n Classwork SP 12 B Pg 113 Q 1 a, c Q 2 b, d Q 3 c, d Q 4 b, d Q 5 a, b n n n Homework SP 12 B Pg 113 Q 1 b, d Q 2 a, c Q 3 a, b Q 4 a, c