Chapter 11 Vectors and the Geometry of Space

Chapter 11 Vectors and the Geometry of Space

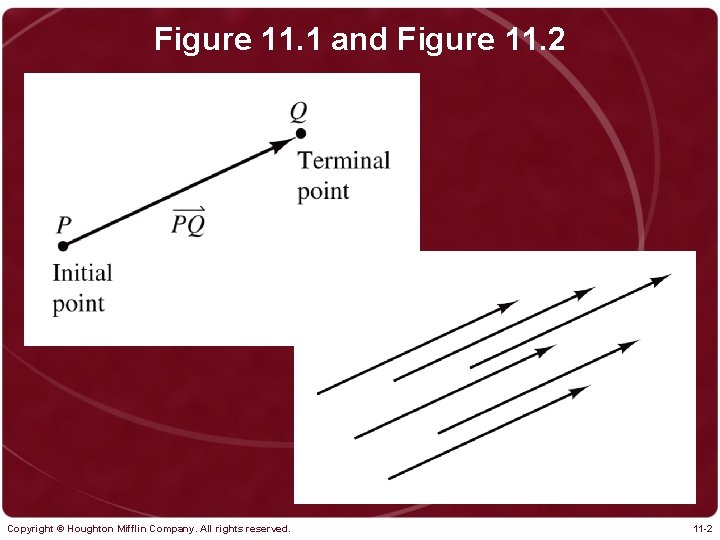
Figure 11. 1 and Figure 11. 2 Copyright © Houghton Mifflin Company. All rights reserved. 11 -2

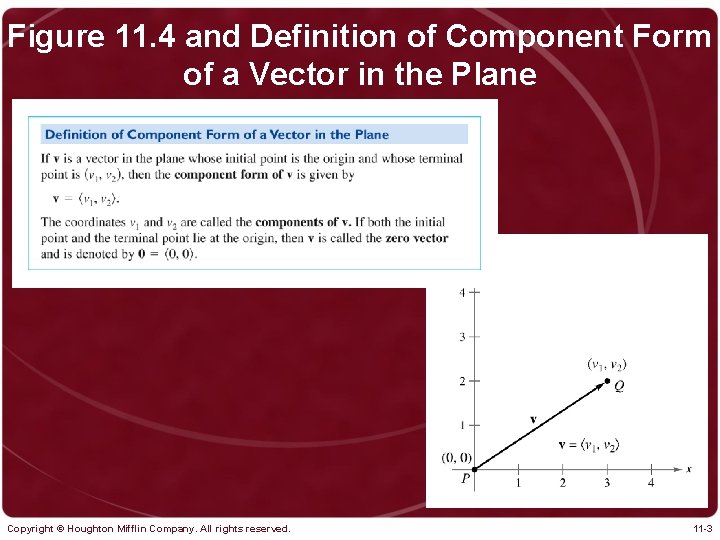
Figure 11. 4 and Definition of Component Form of a Vector in the Plane Copyright © Houghton Mifflin Company. All rights reserved. 11 -3

Definitions of Vector Addition and Scalar Multiplication Copyright © Houghton Mifflin Company. All rights reserved. 11 -4

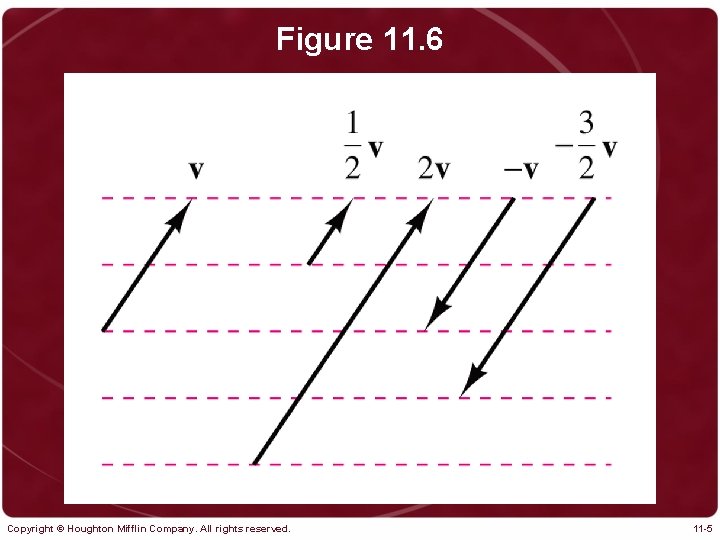
Figure 11. 6 Copyright © Houghton Mifflin Company. All rights reserved. 11 -5

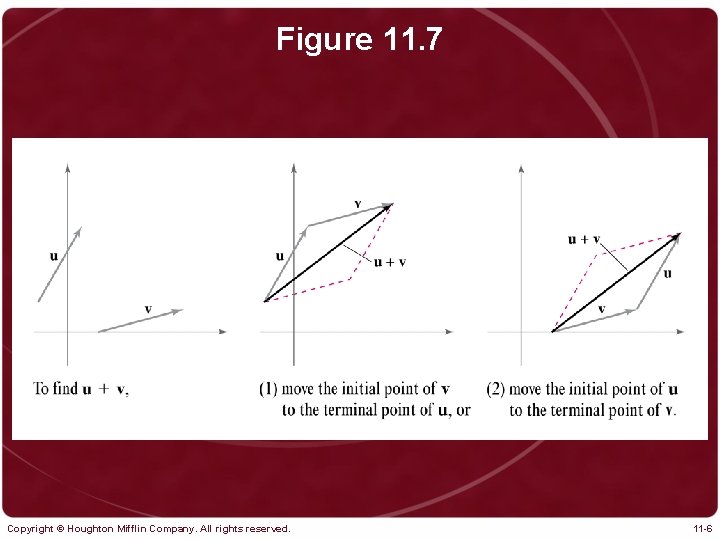
Figure 11. 7 Copyright © Houghton Mifflin Company. All rights reserved. 11 -6

Figure 11. 8 Copyright © Houghton Mifflin Company. All rights reserved. 11 -7

Theorem 11. 1 Properties of Vector Operations Copyright © Houghton Mifflin Company. All rights reserved. 11 -8

Theorem 11. 2 Length of a Scalar Multiple 11 -9

Theorem 11. 3 Unit Vector in the Direction of v Copyright © Houghton Mifflin Company. All rights reserved. 11 -10

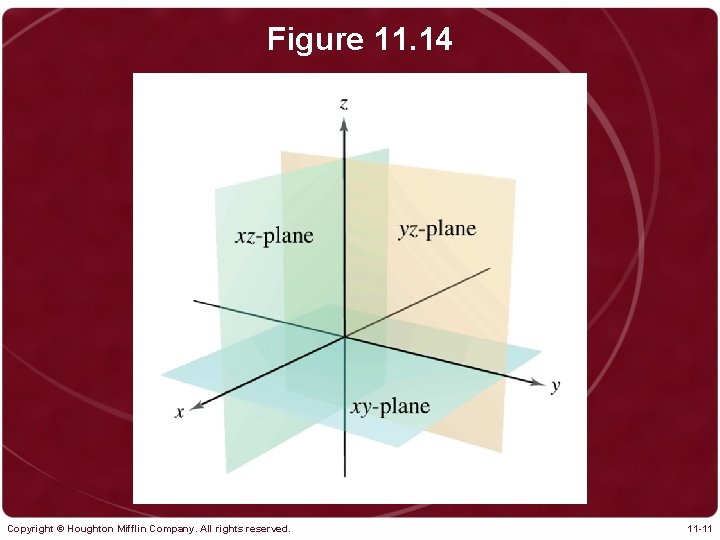
Figure 11. 14 Copyright © Houghton Mifflin Company. All rights reserved. 11 -11

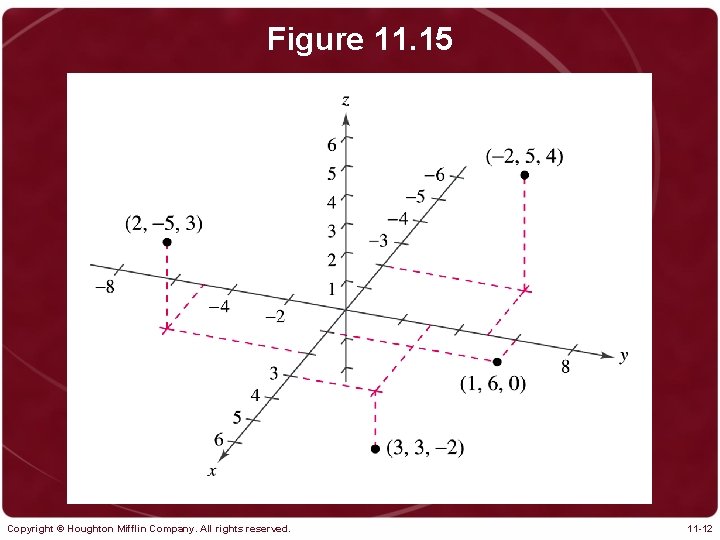
Figure 11. 15 Copyright © Houghton Mifflin Company. All rights reserved. 11 -12

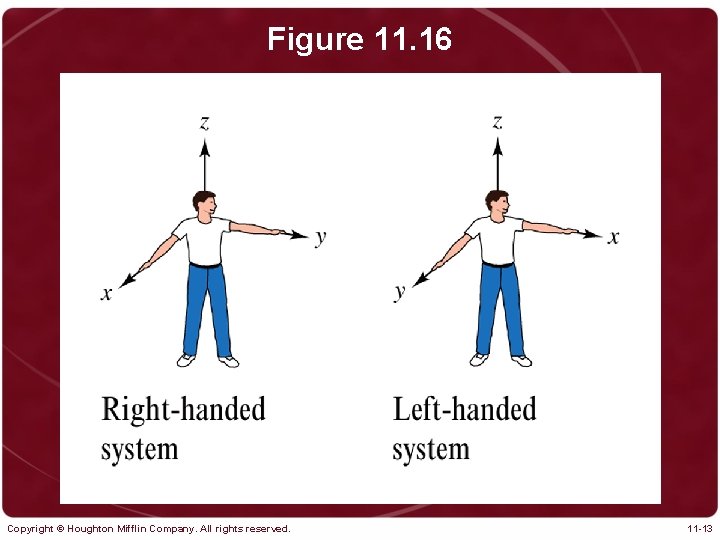
Figure 11. 16 Copyright © Houghton Mifflin Company. All rights reserved. 11 -13

Figure 11. 17 Copyright © Houghton Mifflin Company. All rights reserved. 11 -14

Vectors in Space box Copyright © Houghton Mifflin Company. All rights reserved. 11 -15

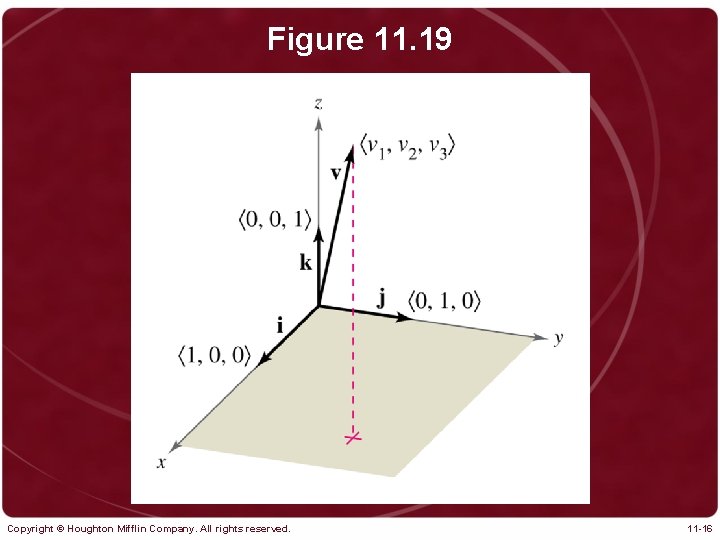
Figure 11. 19 Copyright © Houghton Mifflin Company. All rights reserved. 11 -16

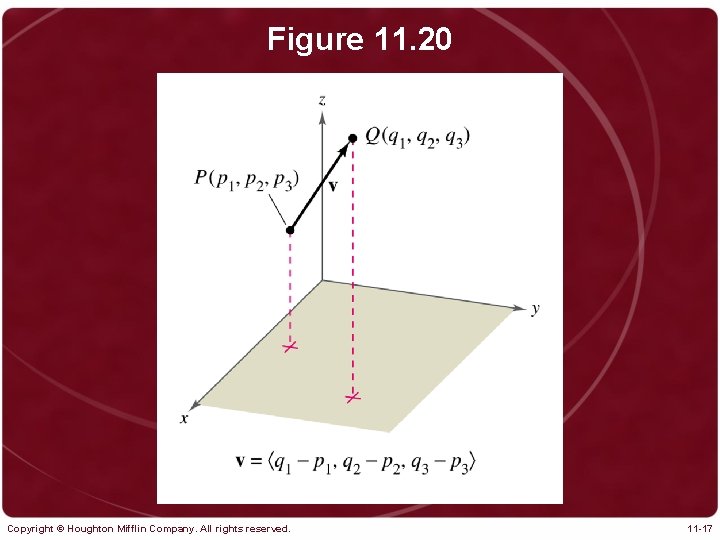
Figure 11. 20 Copyright © Houghton Mifflin Company. All rights reserved. 11 -17

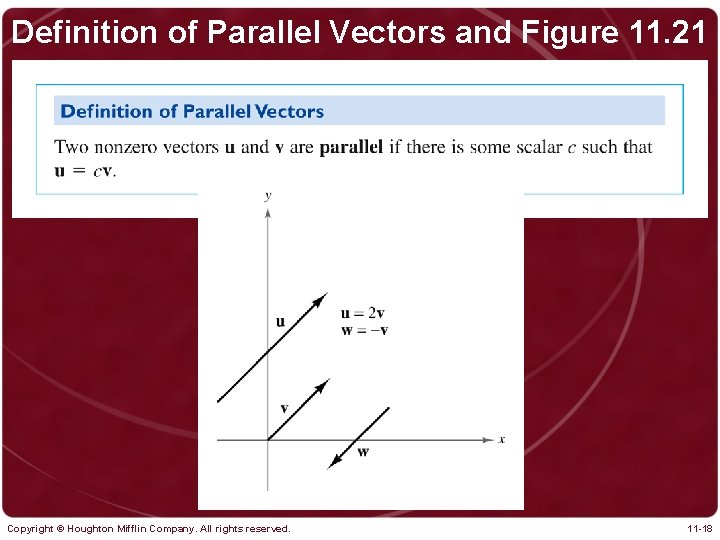
Definition of Parallel Vectors and Figure 11. 21 Copyright © Houghton Mifflin Company. All rights reserved. 11 -18

Definition of Dot Product Copyright © Houghton Mifflin Company. All rights reserved. 11 -19

Theorem 11. 4 Properties of the Dot Product Copyright © Houghton Mifflin Company. All rights reserved. 11 -20

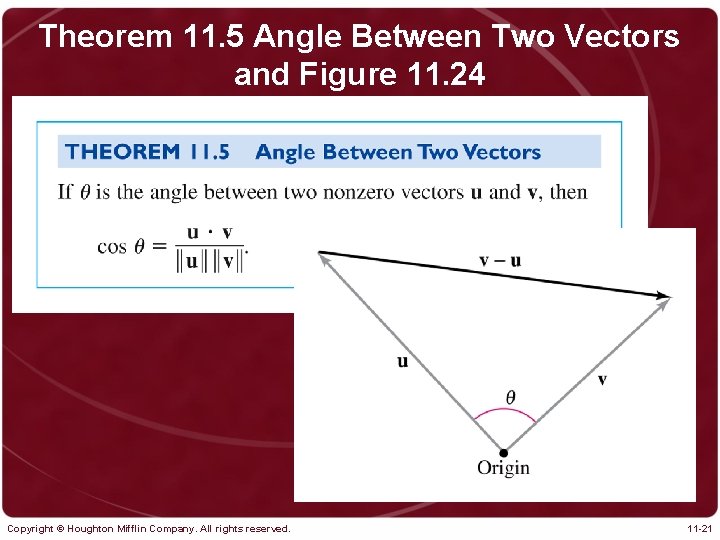
Theorem 11. 5 Angle Between Two Vectors and Figure 11. 24 Copyright © Houghton Mifflin Company. All rights reserved. 11 -21

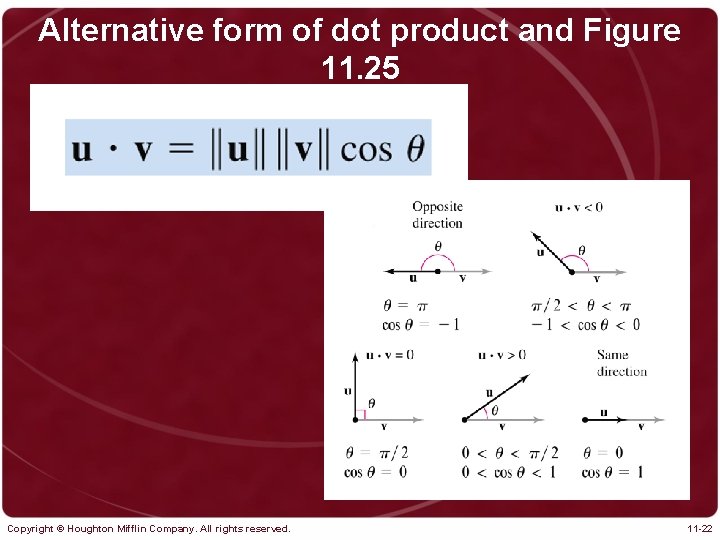
Alternative form of dot product and Figure 11. 25 Copyright © Houghton Mifflin Company. All rights reserved. 11 -22

Definition of Orthogonal Vectors Copyright © Houghton Mifflin Company. All rights reserved. 11 -23

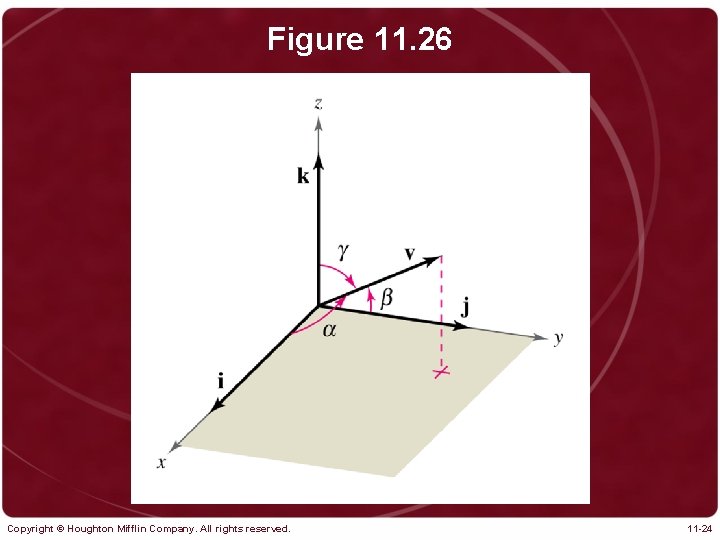
Figure 11. 26 Copyright © Houghton Mifflin Company. All rights reserved. 11 -24

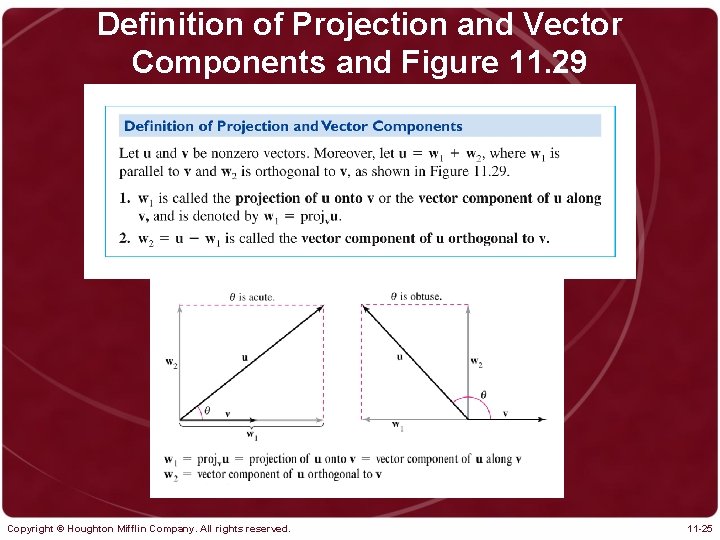
Definition of Projection and Vector Components and Figure 11. 29 Copyright © Houghton Mifflin Company. All rights reserved. 11 -25

Theorem 11. 6 Projection Using the Dot Product Copyright © Houghton Mifflin Company. All rights reserved. 11 -26

Definition of Work and Figure 11. 33 Copyright © Houghton Mifflin Company. All rights reserved. 11 -27

Definition of Cross Product of Two Vectors in Space 11 -28

Theorem 11. 7 Algebraic Properties of the Cross Product Copyright © Houghton Mifflin Company. All rights reserved. 11 -29

Theorem 11. 8 Geometric Properties of the Cross Product Copyright © Houghton Mifflin Company. All rights reserved. 11 -30

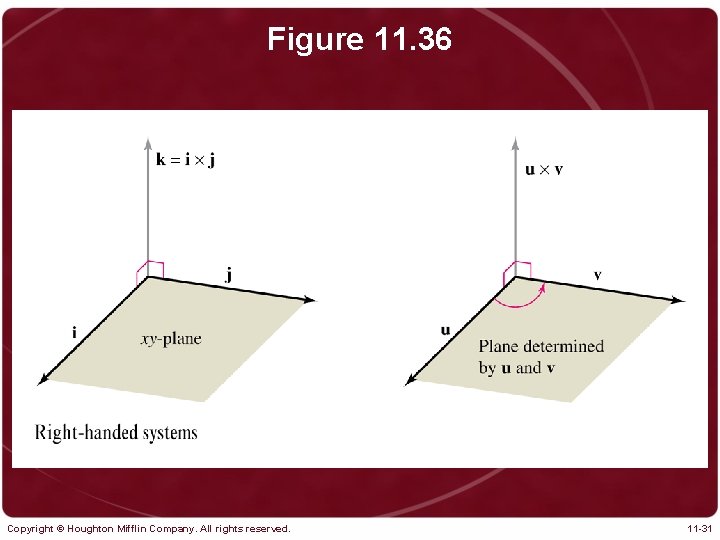
Figure 11. 36 Copyright © Houghton Mifflin Company. All rights reserved. 11 -31

Theorem 11. 9 The Triple Scalar Product Copyright © Houghton Mifflin Company. All rights reserved. 11 -32

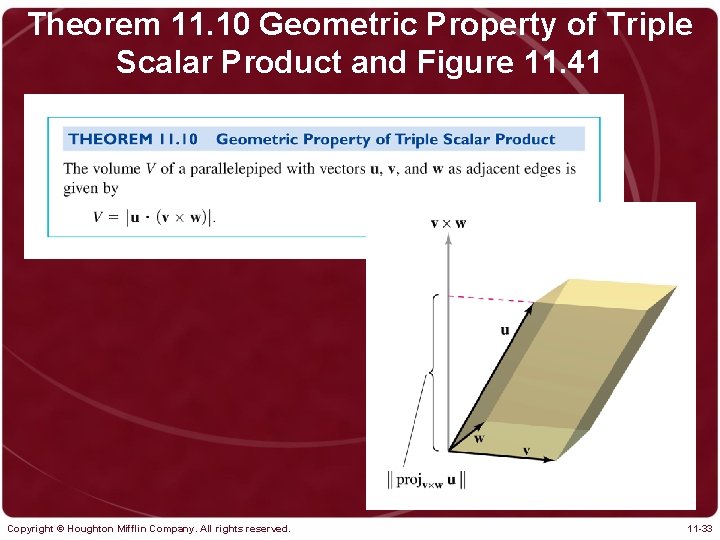
Theorem 11. 10 Geometric Property of Triple Scalar Product and Figure 11. 41 Copyright © Houghton Mifflin Company. All rights reserved. 11 -33

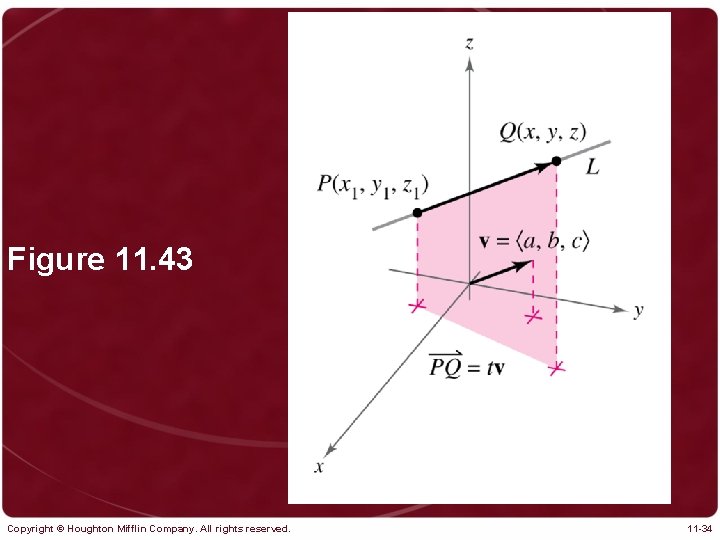
Figure 11. 43 Copyright © Houghton Mifflin Company. All rights reserved. 11 -34

Theorem 11. 11 Parametric Equations of a Line in Space Copyright © Houghton Mifflin Company. All rights reserved. 11 -35

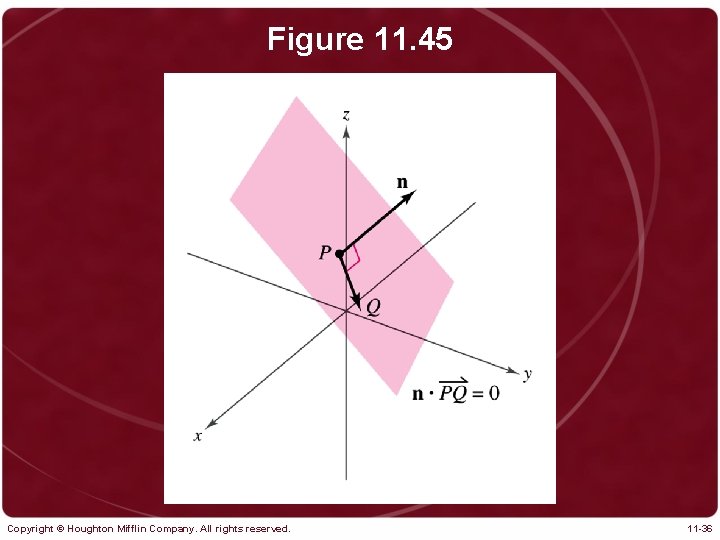
Figure 11. 45 Copyright © Houghton Mifflin Company. All rights reserved. 11 -36

Theorem 11. 12 Standard Equation of a Plane in Space Copyright © Houghton Mifflin Company. All rights reserved. 11 -37

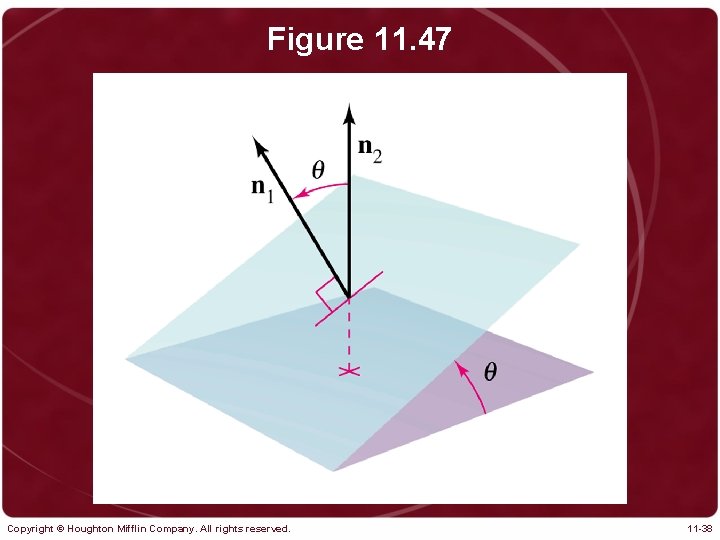
Figure 11. 47 Copyright © Houghton Mifflin Company. All rights reserved. 11 -38

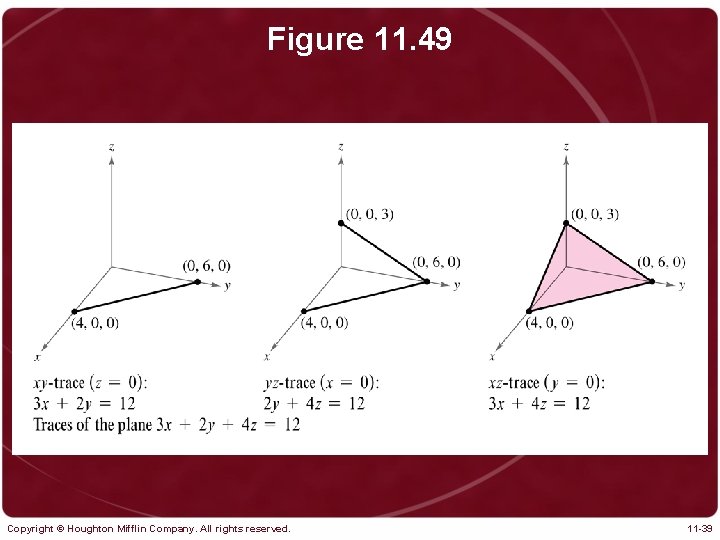
Figure 11. 49 Copyright © Houghton Mifflin Company. All rights reserved. 11 -39

Figure 11. 50 Copyright © Houghton Mifflin Company. All rights reserved. 11 -40

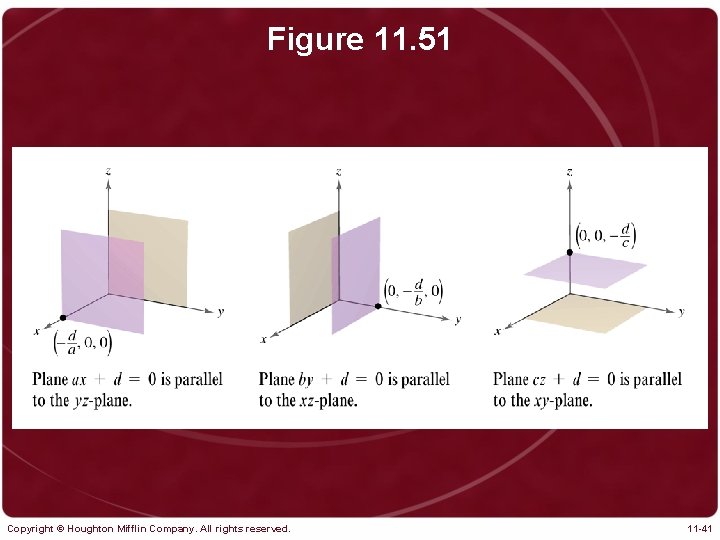
Figure 11. 51 Copyright © Houghton Mifflin Company. All rights reserved. 11 -41

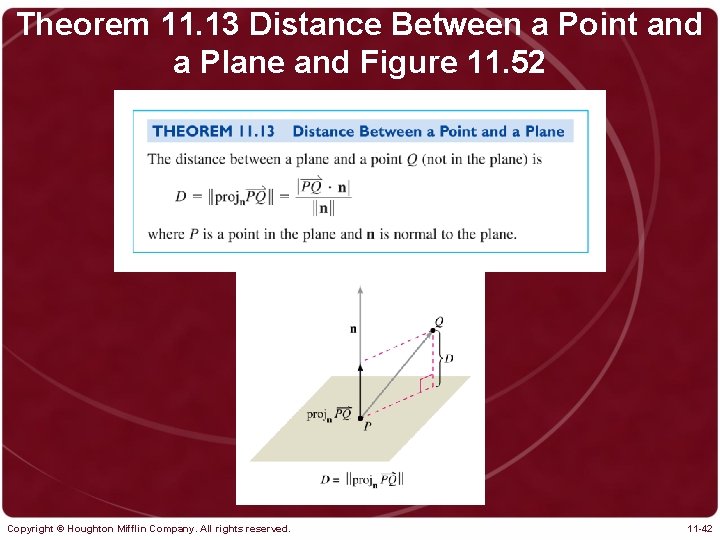
Theorem 11. 13 Distance Between a Point and a Plane and Figure 11. 52 Copyright © Houghton Mifflin Company. All rights reserved. 11 -42

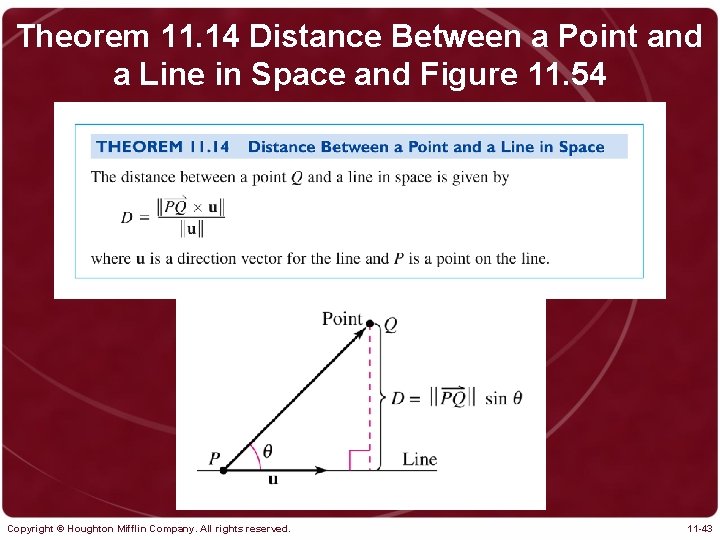
Theorem 11. 14 Distance Between a Point and a Line in Space and Figure 11. 54 Copyright © Houghton Mifflin Company. All rights reserved. 11 -43

Definition of a Cylinder and Figure 11. 56 Copyright © Houghton Mifflin Company. All rights reserved. 11 -44

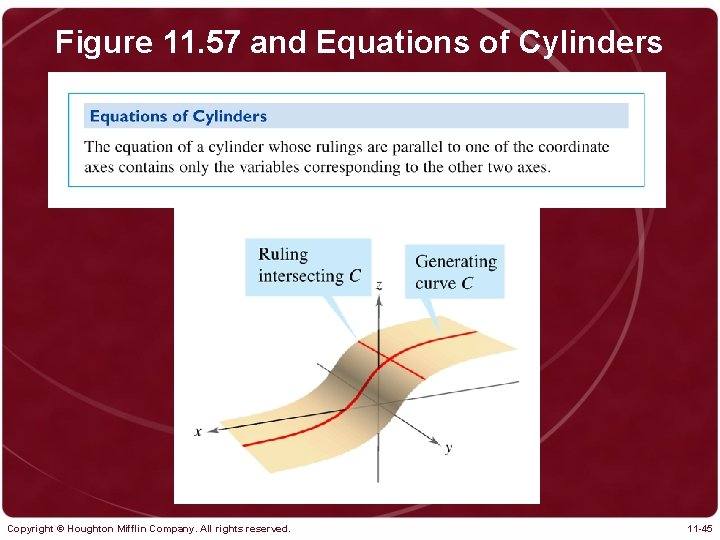
Figure 11. 57 and Equations of Cylinders Copyright © Houghton Mifflin Company. All rights reserved. 11 -45

Quadric Surface Copyright © Houghton Mifflin Company. All rights reserved. 11 -46

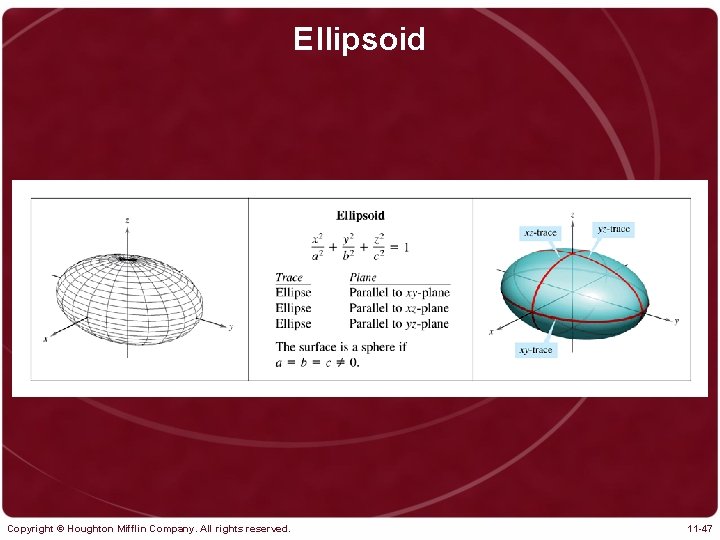
Ellipsoid Copyright © Houghton Mifflin Company. All rights reserved. 11 -47

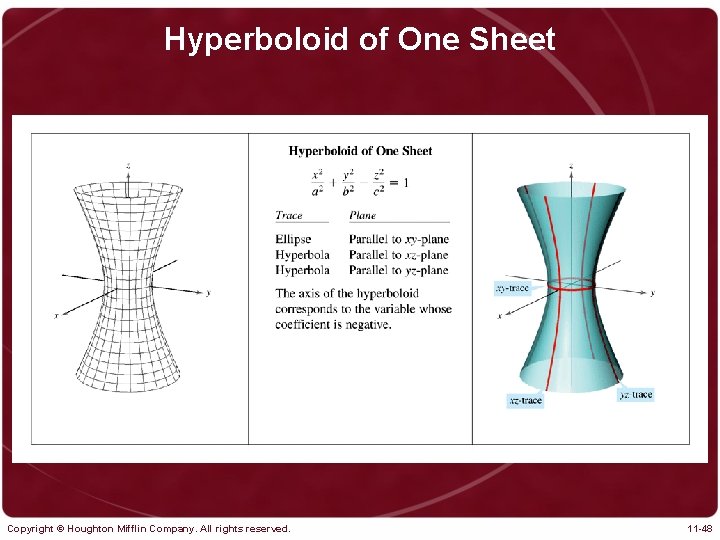
Hyperboloid of One Sheet Copyright © Houghton Mifflin Company. All rights reserved. 11 -48

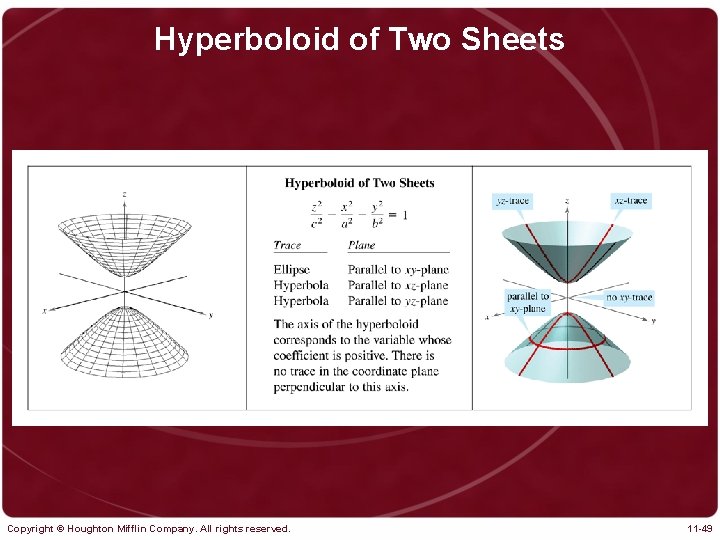
Hyperboloid of Two Sheets Copyright © Houghton Mifflin Company. All rights reserved. 11 -49

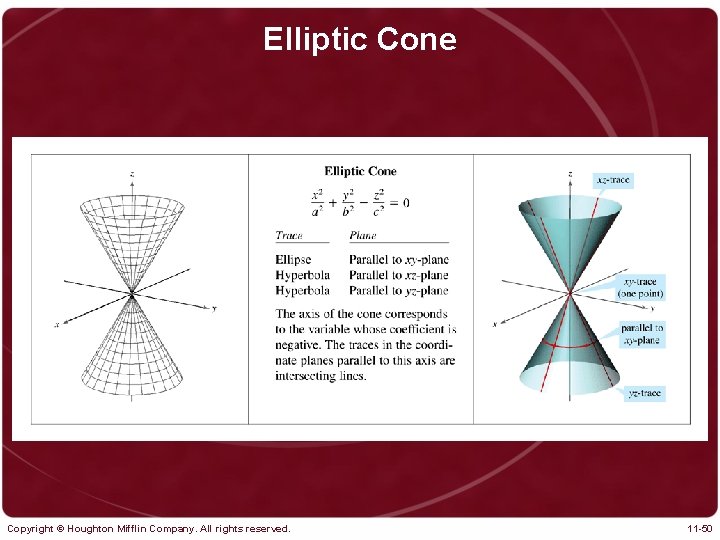
Elliptic Cone Copyright © Houghton Mifflin Company. All rights reserved. 11 -50

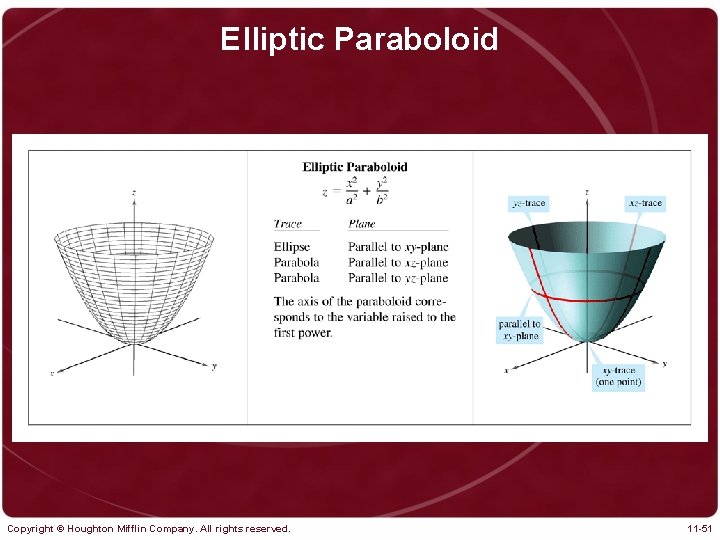
Elliptic Paraboloid Copyright © Houghton Mifflin Company. All rights reserved. 11 -51

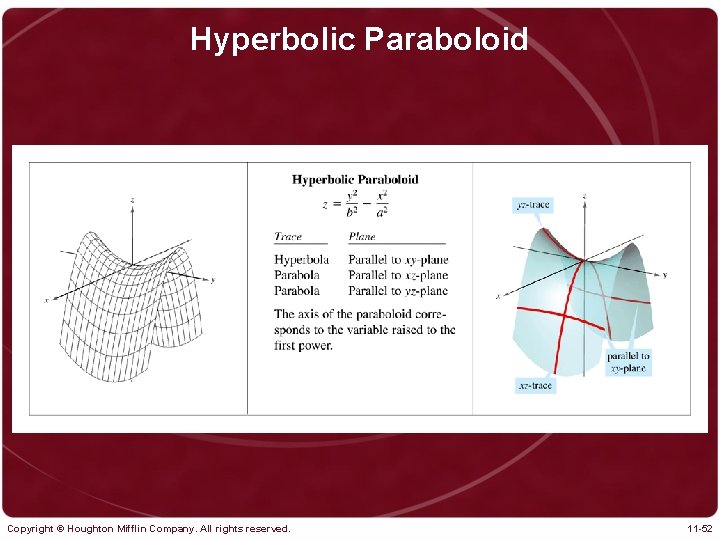
Hyperbolic Paraboloid Copyright © Houghton Mifflin Company. All rights reserved. 11 -52

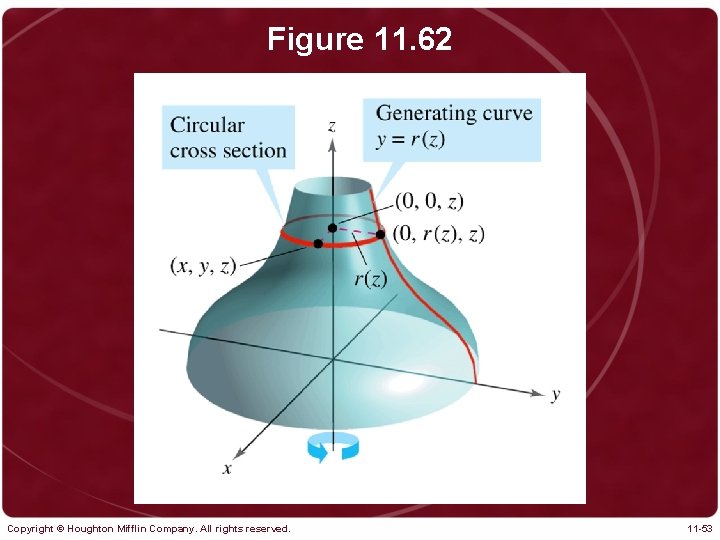
Figure 11. 62 Copyright © Houghton Mifflin Company. All rights reserved. 11 -53

Surface of Revolution Copyright © Houghton Mifflin Company. All rights reserved. 11 -54

The Cylindrical Coordinate System Copyright © Houghton Mifflin Company. All rights reserved. 11 -55

Figure 11. 66 Copyright © Houghton Mifflin Company. All rights reserved. 11 -56

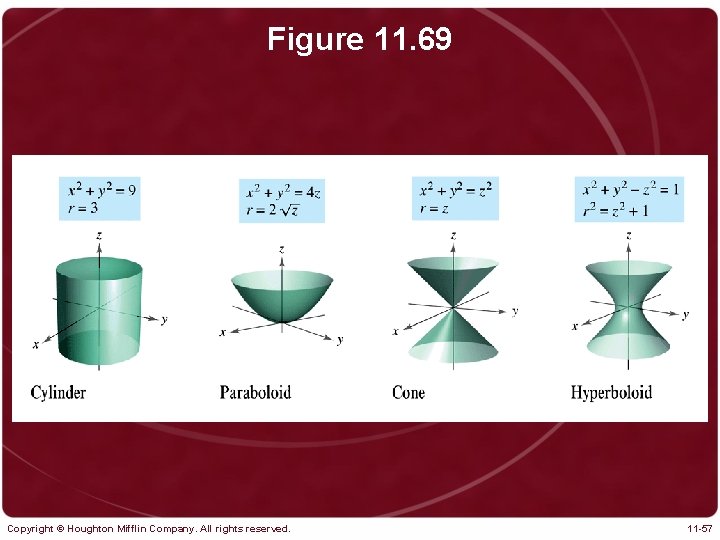
Figure 11. 69 Copyright © Houghton Mifflin Company. All rights reserved. 11 -57

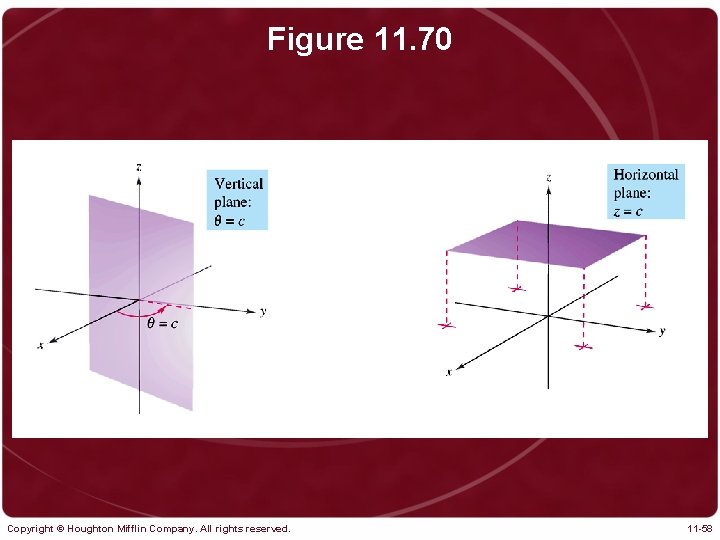
Figure 11. 70 Copyright © Houghton Mifflin Company. All rights reserved. 11 -58

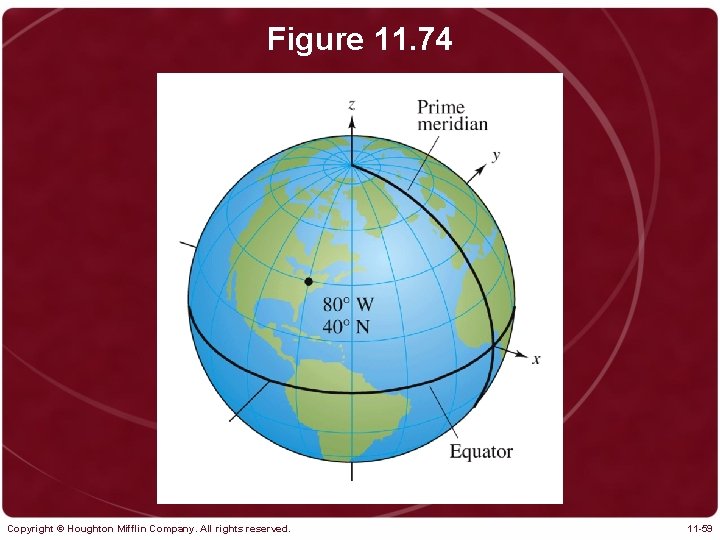
Figure 11. 74 Copyright © Houghton Mifflin Company. All rights reserved. 11 -59

The Spherical Coordinate System Copyright © Houghton Mifflin Company. All rights reserved. 11 -60

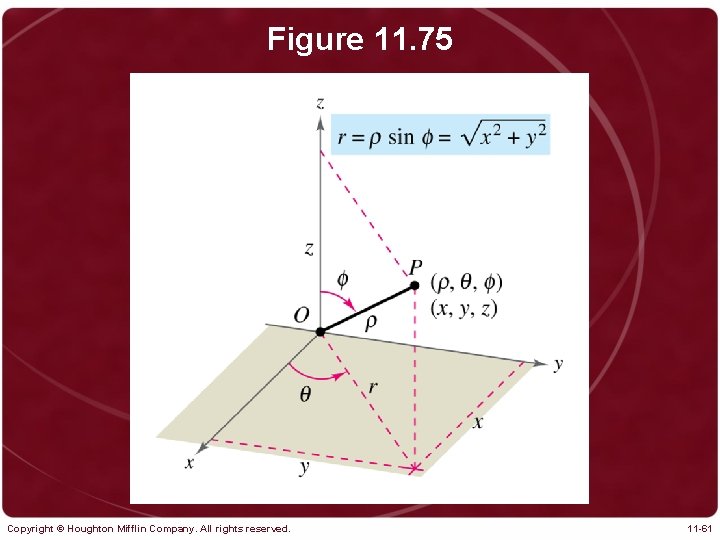
Figure 11. 75 Copyright © Houghton Mifflin Company. All rights reserved. 11 -61

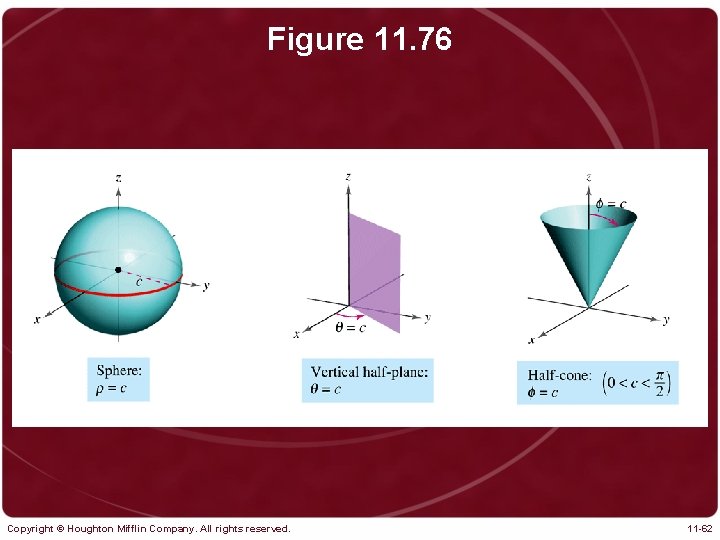
Figure 11. 76 Copyright © Houghton Mifflin Company. All rights reserved. 11 -62