Chapter 11 The Normal Distributions Note Normal distributions

Chapter 11 The Normal Distributions Note: Normal distributions are the most popular probability models in statistics. Other popular models include binomial distributions, t distributions, etc. 10/31/2021 1
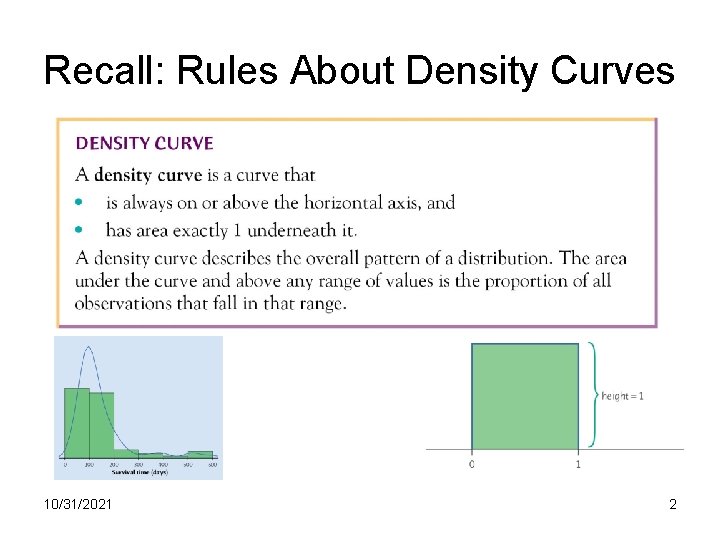
Recall: Rules About Density Curves 10/31/2021 2
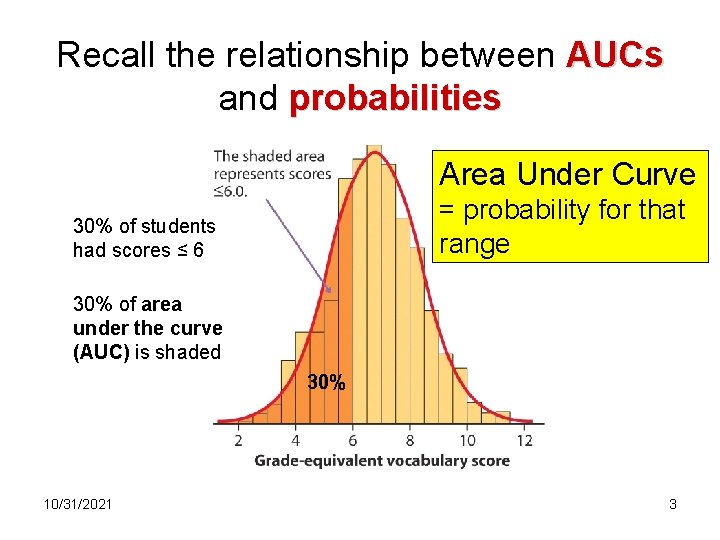
Recall the relationship between AUCs and probabilities Area Under Curve = probability for that range 30% of students had scores ≤ 6 30% of area under the curve (AUC) is shaded 30% 10/31/2021 3
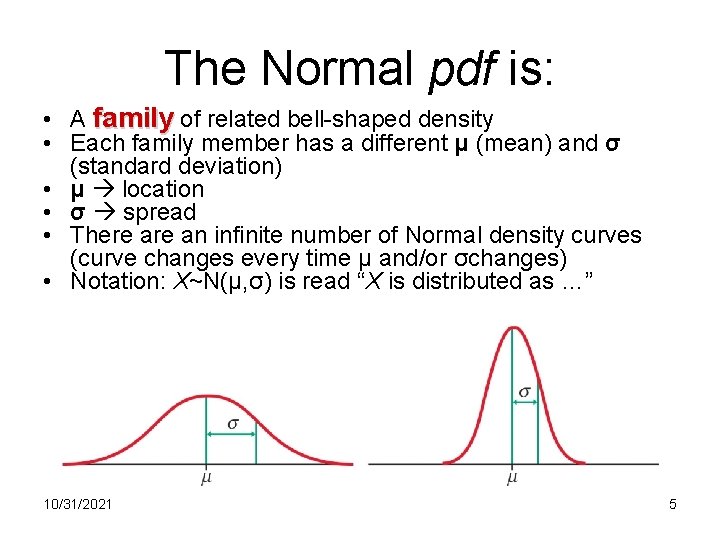
The Normal pdf is: • A family of related bell-shaped density • Each family member has a different μ (mean) and σ (standard deviation) • μ location • σ spread • There an infinite number of Normal density curves (curve changes every time µ and/or σchanges) • Notation: X~N(µ, σ) is read “X is distributed as …” 10/31/2021 5

Draw Normal curves accurately! • Symmetrical around μ • Infection points at μ ± σ • Horizontal asymptotes Drawing a half circle is not acceptable 10/31/2021 6

68 -95 -99. 7 Rule • μ ± 1σ contains 68% of AUC • μ ± 2σ contains 95% of AUC • μ ± 3σ contains 99. 7% of AUC The 68 -95 -99. 7 rule applies only to Normal densities 10/31/2021 7

68 -95 -99. 7 Rule - Example • Assume male height (X) has Normal distribution with μ = 70. 0 inches and σ = 2. 8 inches • Notation: Notation X~ N(70, 2. 8) • µ = 70. 0 2. 8 = 67. 2 to 72. 8 68% of men between 67. 2 and 72. 8 inches tall • µ 2 = 70. 0 2(2. 8) = 64. 4 to 75. 6 (inches) 95% in this range • µ 3 = 70. 0 3(2. 8) = 61. 6 to 78. 4 (inches) 99. 7% in this range 8
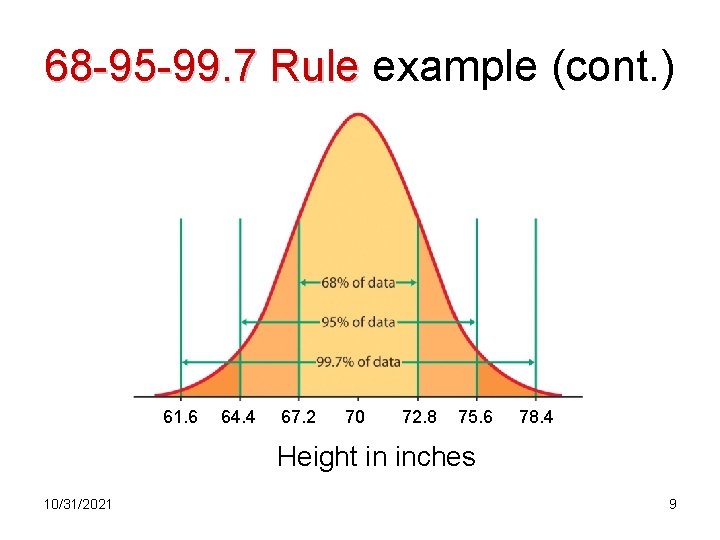
68 -95 -99. 7 Rule example (cont. ) 61. 6 64. 4 67. 2 70 72. 8 75. 6 78. 4 Height in inches 10/31/2021 9

Example 2 (Male Height) What proportion of men are less than 72. 8" tall? X~ N(70, 2. 8) By 68 -95 -99. 7 rule 68% Total AUC =100% 32% split evenly in tails 16% 16% + 68% = 84% 10/31/2021 84% of AUC to the left of 72. 8 10

Finding Normal Probabilities: Method 1. Draw an reasonably accurate Normal curve with landmarks at µ and µ ±σ 2. Place values on the curve & shade relevant area 3. Standardize values (i. e. , z scores) 4. Use Table A to determine the AUC 10/31/2021 11
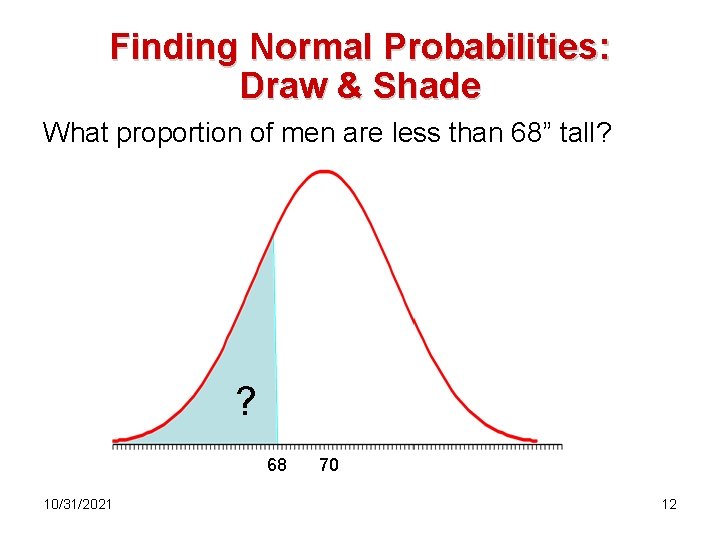
Finding Normal Probabilities: Draw & Shade What proportion of men are less than 68” tall? ? 68 10/31/2021 70 12

Finding Normal Probabilities: Standardize In X~N(70, 2. 8), the value 68 has: This indicates that 68 is 0. 71 standard deviations below the mean 10/31/2021 13
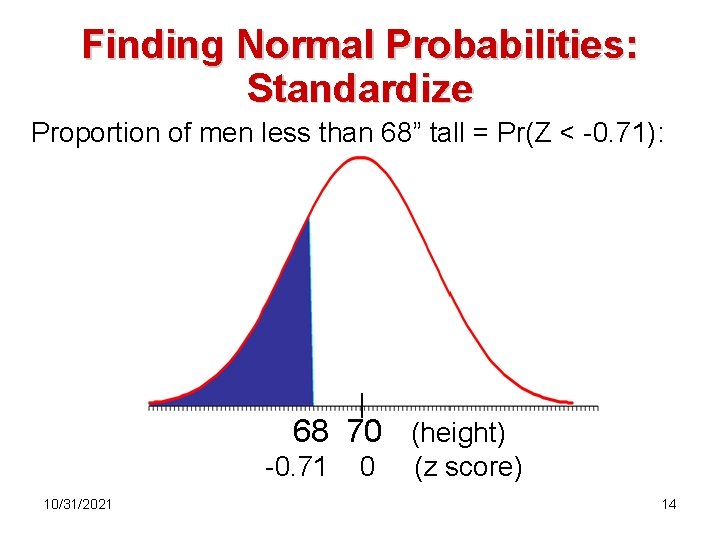
Finding Normal Probabilities: Standardize Proportion of men less than 68” tall = Pr(Z < -0. 71): 68 70 (height) -0. 71 10/31/2021 0 (z score) 14
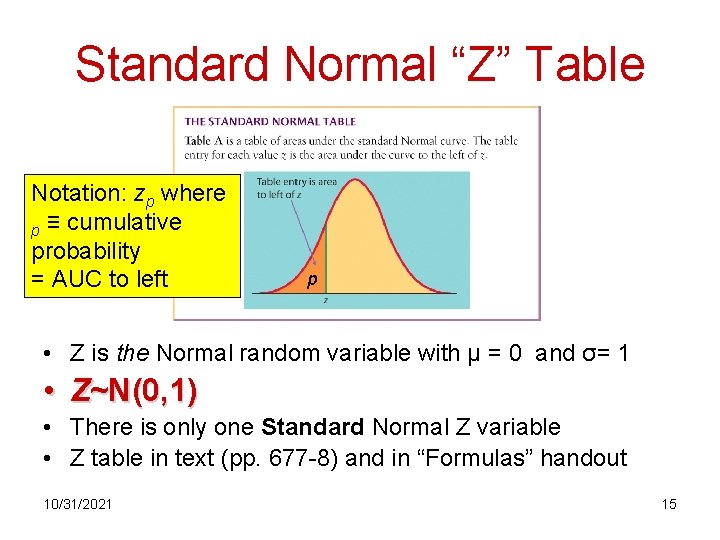
Standard Normal “Z” Table Notation: zp where p ≡ cumulative probability = AUC to left p • Z is the Normal random variable with µ = 0 and σ= 1 • Z~N(0, 1) • There is only one Standard Normal Z variable • Z table in text (pp. 677 -8) and in “Formulas” handout 10/31/2021 15
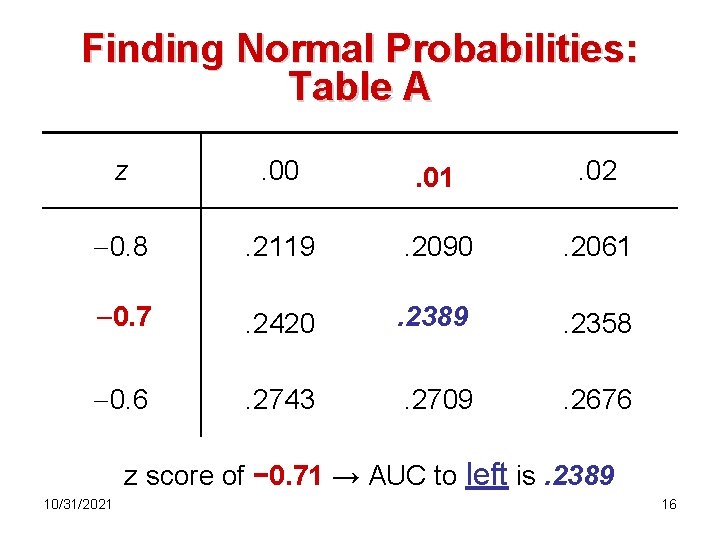
Finding Normal Probabilities: Table A z . 00 . 01 . 02 0. 8 . 2119 . 2090 . 2061 0. 7 . 2420 . 2389 . 2358 0. 6 . 2743 . 2709 . 2676 z score of − 0. 71 → AUC to left is. 2389 10/31/2021 16
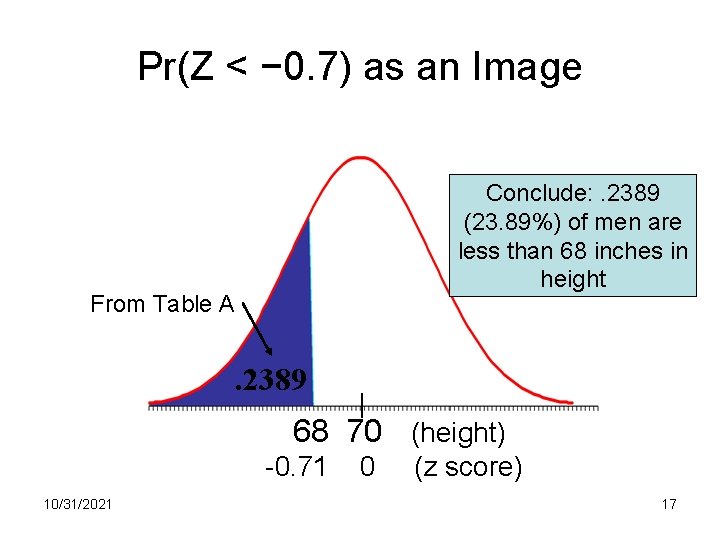
Pr(Z < − 0. 7) as an Image Conclude: . 2389 (23. 89%) of men are less than 68 inches in height From Table A . 2389 68 70 (height) -0. 71 10/31/2021 0 (z score) 17
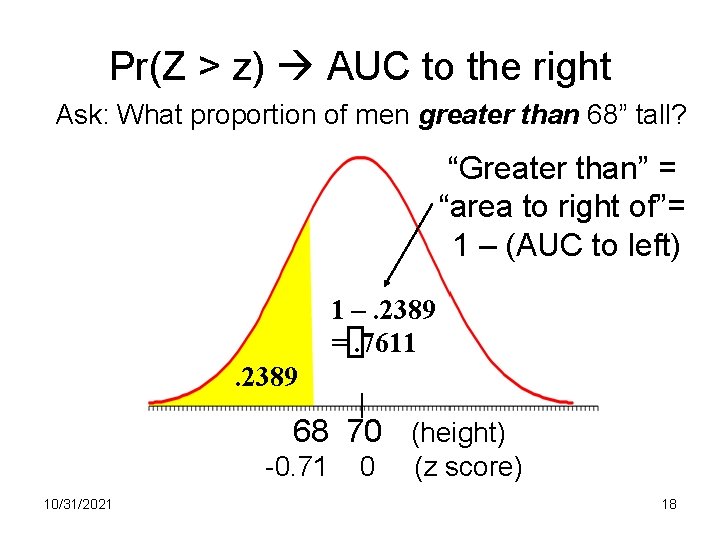
Pr(Z > z) AUC to the right Ask: What proportion of men greater than 68” tall? “Greater than” = “area to right of”= 1 – (AUC to left) 1 –. 2389 =. 7611. 2389 68 70 (height) -0. 71 10/31/2021 0 (z score) 18

AUC Between Two Points Total AUC = 1. Therefore: Pr(a < Z < b) = Pr(Z < b) – Pr(Z < a) . 6915 -1. 28 0. 5 Pr(− 1. 28 < Z < 0. 5) = Pr(Z < 0. 5) =. 6915 =. 5912 . 1003 -1. 28 – Pr(Z < − 1. 28) –. 1003

Finding z percentiles and associated values At times, we must find the z value or X value that is associated with a given probability. To do this: 1. State the problem 2. Sketch the curve 3. Look up the related z-score is Z table 4. If you need to know X, “unstandardize” z with this formula: 10/31/2021 20
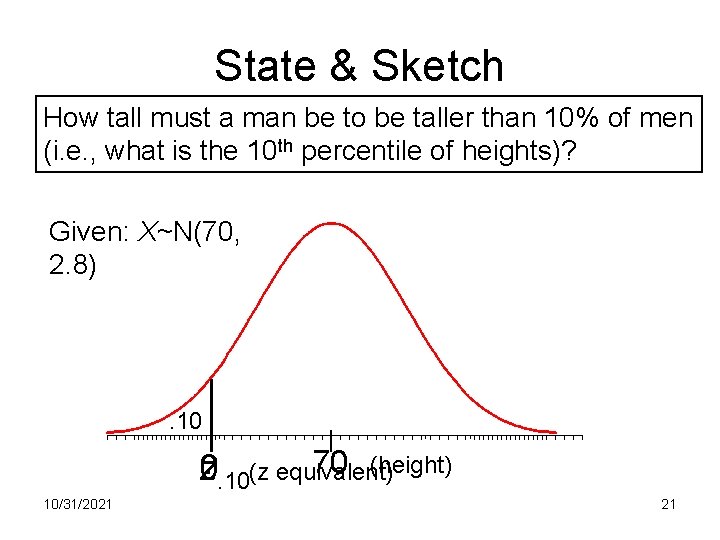
State & Sketch How tall must a man be to be taller than 10% of men (i. e. , what is the 10 th percentile of heights)? Given: X~N(70, 2. 8) . 10 70 (height) ? . 10(z equivalent) z 0 10/31/2021 21
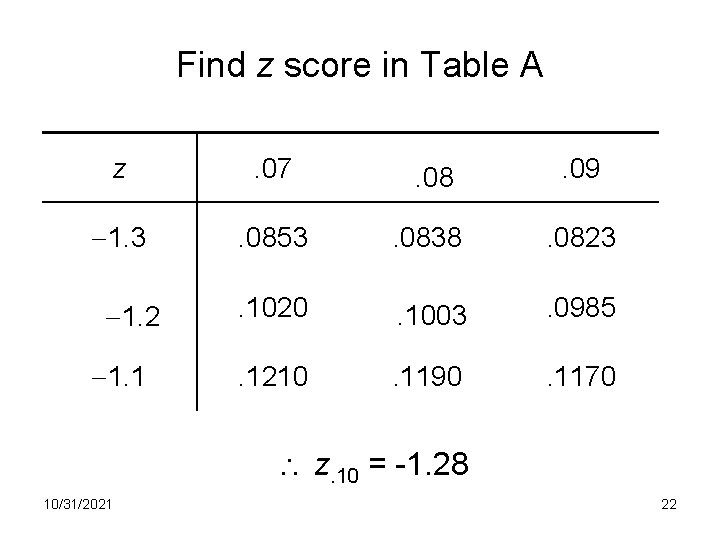
Find z score in Table A z . 07 . 08 . 09 1. 3 . 0853 . 0838 . 0823 . 1020 . 1003 . 0985 . 1210 . 1190 . 1170 1. 2 1. 1 z. 10 = -1. 28 10/31/2021 22
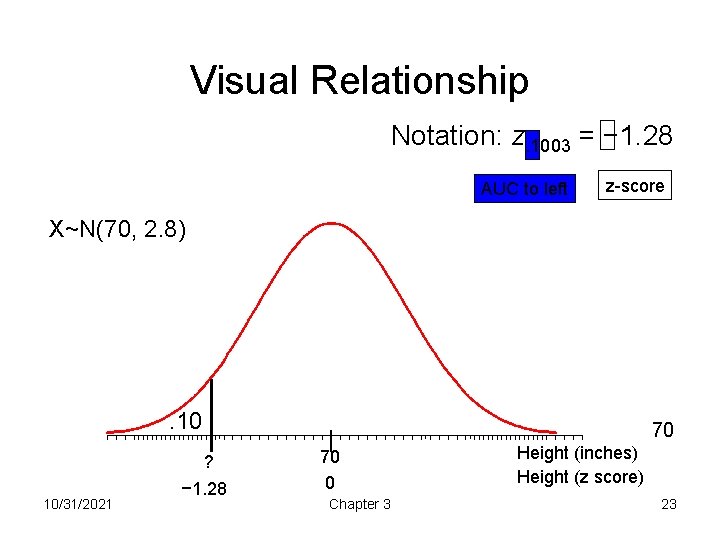
Visual Relationship Notation: z. 1003 = − 1. 28 AUC to left z-score X~N(70, 2. 8) . 10 70 ? 10/31/2021 − 1. 28 70 0 Chapter 3 Height (inches) Height (z score) 23

Unstandardize & Conclude • x = μ + z∙σ = 70 + ( 1. 28 )(2. 8) = 70 + ( 3. 58) = 66. 42 • Conclude: A man who is 66. 42 inches in height is taller than 10% of men • We can also conclude that he is shorter than (1 – 10%) or 90% of men 10/31/2021 Chapter 3 24
- Slides: 23