Chapter 11 Sampling Design Chapter Objectives define sampling

Chapter 11 Sampling Design

Chapter Objectives • define sampling, sample, population, element, subject and sampling frame • describe and discuss the different probability and nonprobability sampling designs • identify the use of appropriate sampling designs for different research purposes • discuss precision and confidence • estimate sample size • discuss efficiency in sampling • discuss generalisability in the context of sampling designs

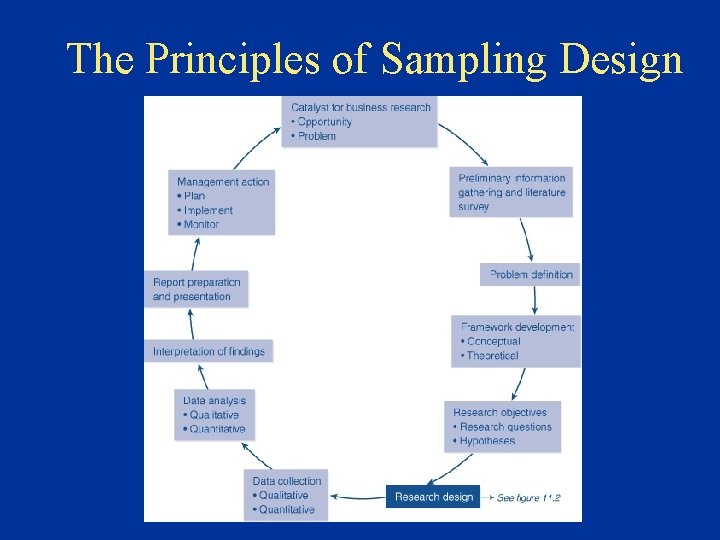
The Principles of Sampling Design

Population, Element, Sampling Frame, Sample and Subject • Population (or target population) • entire group of people, events or things of interest that the researcher wishes to investigate • Element • a single member of the population • Sampling Frame • a listing of all the elements in the population from which the sample is drawn • Sample • a subset of the population • Subject • a single member of the sample

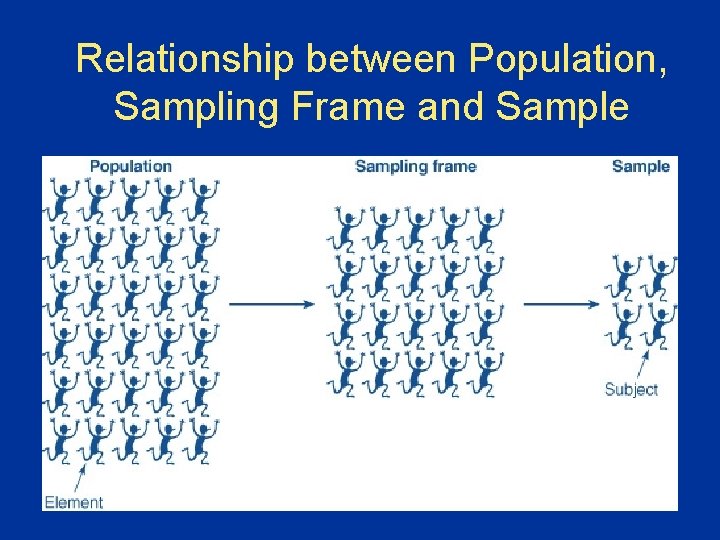
Relationship between Population, Sampling Frame and Sample

Relationship between Sample Statistics and Population Parameters

Advantages of Sampling • Less costs – cheaper than studying whole population • Less errors due to less fatigue – better results • Less time – quicker • Destruction of elements avoided – eg bulbs

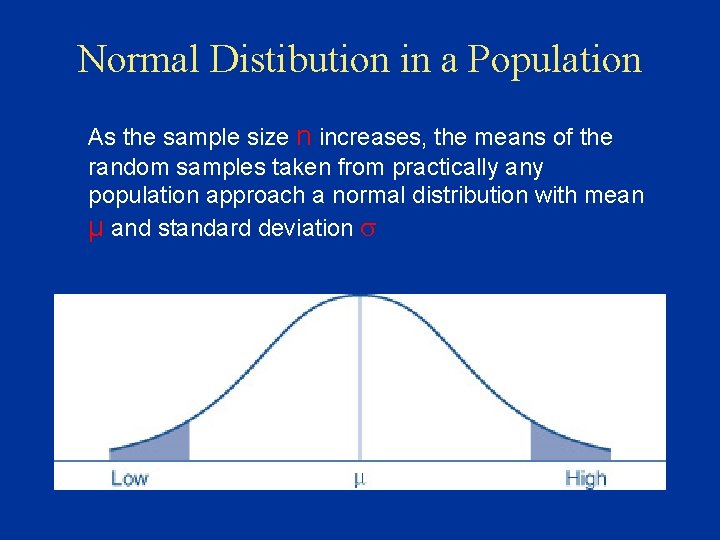
Normal Distibution in a Population As the sample size n increases, the means of the random samples taken from practically any population approach a normal distribution with mean μ and standard deviation

Representativeness of Samples • If the sample mean is much > than the population mean μ then the sample would overestimate the true population mean • If the sample mean is much < than the population mean μ then the sample would underestimate the true population mean • The more representative the sample is of the population, the more generalisable are the findings of the research.

Preparing a Sampling Design

Probability & Non-probability Sampling • Probability Sampling – the elements in the population have some known chance or probability of being selected as sample subjects • Non-probability Sampling – the elements do not have a known or predetermined chance of being selected as subjects

Probability Sampling • Simple random sampling – every element in the population has a known and equal chance of being selected as a subject • Complex (or restricted) probability sampling – procedures to ensure practical viable alternatives to simple random sampling, at lower costs, and greater statistical efficiency

Simple Random Sampling • Is the most representative of the population for most purposes • Disadvantages are: – Most cumbersome and tedious – The entire listing of elements in population frequently unavailable – Very expensive – Not the most efficient design

Complex Probability Sampling • • • Systematic sampling Stratified random sampling Cluster sampling Area sampling Double sampling

Systematic Sampling • Every nth element in the population starting with a randomly chosen element • Example: – Want a sample of 35 households from a total of 260 houses. Could sample every 7 th house starting from a randomly chosen number from 1 to 10. If that random number is 7, sample 35 houses starting with 7 th house (14 th house, 21 st house, etc) – Possible problem is that there could be systematic bias. eg every 7 th house could be a corner house, with different characteristics of both house and dwellers.

Stratified Random Sampling • Comprises sampling from populations segregated into a number of mutually exclusive sub-populations or strata. Eg – University students divided into juniors, seniors, etc – Employees stratified into clerks, supervisors, managers, etc • Homogeneity within stratum and heterogeneity between strata • Statistical efficiency greater in stratified samples • Sub-groups can be analysed • Different methods of analysis can be used for different sub-groups.

Stratified Random Sampling Example Stratum Clerks Middle Managers Top Managers Motivation Level Low Very high Medium Combined X would not discrimate among groups • Stratified Sampling – Proportionate sampling – Disproportionate sampling

Proportionate & Disproportionate Stratified Random Sampling

Cluster Sampling • Take clusters or chunks of elements for study – Eg, sample all students in MGMT 303 and MGMT 304 to study the characteristics of Management Science majors • Advantage of cluster sampling is lower costs • Statistically it is less efficient than other probability sampling procedures discussed so far Area Sampling: • Cluster sampling confined to a particular area – Eg, sampling residents of a particular locality, county, etc

Double Sampling • Collect preliminary data from a sample, and choose a sub-sample of that sample for more detailed investigation. • Example: – Conduct unstructured interviews with a sample of 50. – Repeat a structured interview with 30 from the 50 originally sampled.

Non-probability Sampling • Convenience sampling – Survey whoever is easily available – Used for quick diagnosis of situations • Simplest and cheapest • Least reliable • Purposive sampling – Judgement sampling – Snowball sampling – Quota sampling

Judgement Sampling • Involves the choice of subjects who are in the best position to provide the information required • Experts’ opinions could be sought – Eg, Doctors surveyed for cancer causes

Snowball Sampling • Used when elements in population have specific characteristics or knowledge, but are very difficult to locate and contact. • Initial sample group can be selected by probability or non-probability methods, but new subjects are selected based on information provided by initial subjects. – Eg, used to locate members of different stakeholder groups regarding their opinions of a new public works project.

Quota Sampling • • Quotas for numbers or proportion of people to be sampled, established. Examples: 1) survey for research on dual career families: 50% working men and 50% working women surveyed. 2) Women in management survey: 70% women surveyed and 30% men surveyed.

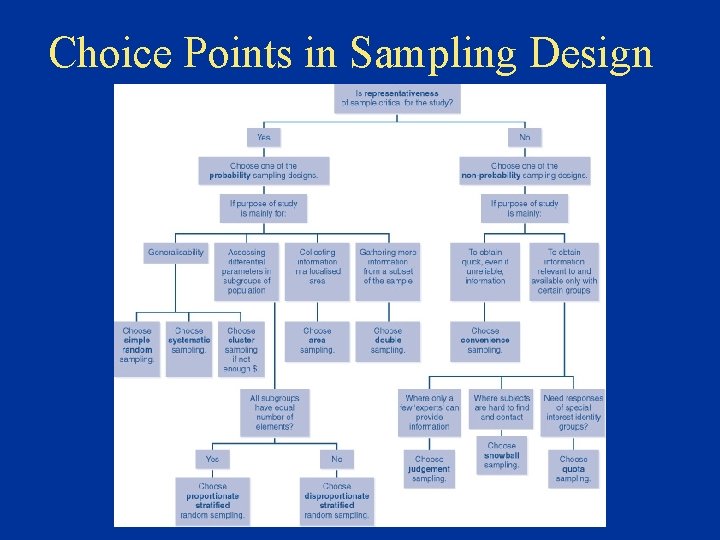
Choice Points in Sampling Design

Precision and Confidence • Precision – refers to how close the sample estimate eg X is to the true population characteristic( ) depends on the variablity in the sampling distribution of the mean, ie the standard error ( S X ) – indicates the confidence interval within which the population mean can be estimated ( = X + KS X ) • Confidence – reflects the level of certainty that the sample estimates will actually hold true for the population – bias is absent from the data – accuracy is reflected by the confidence level ( K )

Standard Error = standard deviation of the sample = sample size = standard error or standard deviation of the sample mean

Characteristics of the Standard Error • The smaller the standard deviation of the population, the smaller the standard error and the greater the precision • The standard error varies inversely with the square root of the sample size. Hence the larger the n, the smaller the standard error, and the greater the precision.

Confidence Interval for the Mean = population mean = sample mean = standard error = z statistic for large samples ≥ 30 = t statistic for small samples < 30

Confidence Levels • For large samples, K = z score = 1. 65 for 90% confidence level = 1. 96 for 95% confidence level = 2. 58 for 99% confidence level • Example: a 95% confidence interval for mean purchases (μ) by customers based on a sample mean of $105 with a standard error of $1. 43 is: μ = 105 ± 1. 96*1. 43 = 105 ± 2. 80 Hence μ would fall between $102. 20 and $107. 80

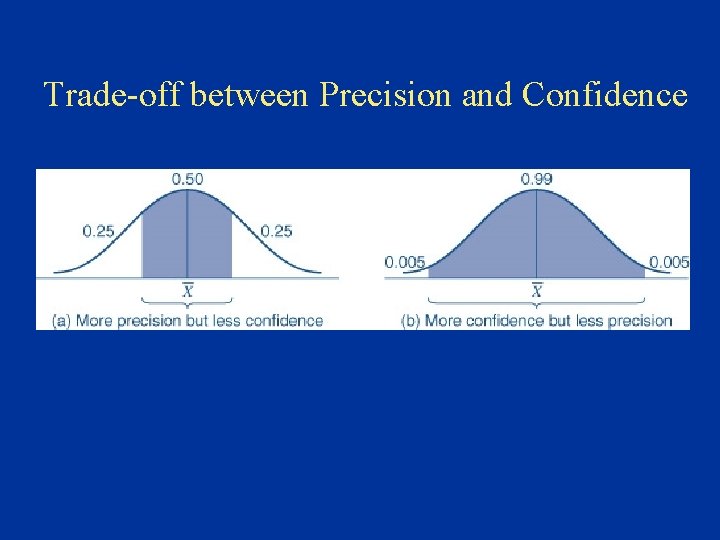
Trade-off between Precision and Confidence

Determining the Sample Size Example: Suppose a manager wants to be 95% confident that withdrawals from a bank will be within a confidence level of ± $500. From a sample of customers the standard deviation S was calculated as $3500. What sample size is needed? The expression is equivalent to the precision or admissible margin of error. Let this be E. or

Determining the Sample Size (cont’d) Rearranging these terms, a formula for the sample size n is: Substituting K=1. 96 (95% confidence), S=3500, and E=500 into this equation, provides the sample size n:

Roscoe’s Rules of Thumb for Determining Sample Size • Sample sizes larger than 30 and smaller than 500 are appropriate for most research • Minimum sample size of 30 for each subcategory is usually necessary • In multivariate research, the sample size should be several times as large as the number of variables in the study • For simple experimental research, successful research is possible with samples as small as 10 to 20

Efficiency in Sampling If n is constant, you should get a smaller or For the same smaller n , you should use a

Review of Sample Size Decisions • How much precision is wanted in estimating the population characteristics, ie what is the margin of admissible error or confidence interval? • How much confidence is really needed. How much risk can we take of making errors in estimating the population parameters (ie confidence level)? • How much variability is in the population? The greater the variability, the larger the sample size needed. • Cost and time constraints • The size of the population (N) itself