CHAPTER 11 Priority Queues and Heaps Java Software

CHAPTER 11: Priority Queues and Heaps Java Software Structures: Designing and Using Data Structures Third Edition John Lewis & Joseph Chase Addison Wesley is an imprint of © 2010 Pearson Addison-Wesley. All rights reserved.

Chapter Objectives • Define a heap abstract data structure • Demonstrate how a heap can be used to solve problems • Examine various heap impmentations • Compare heap implementations 1 -2 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -2

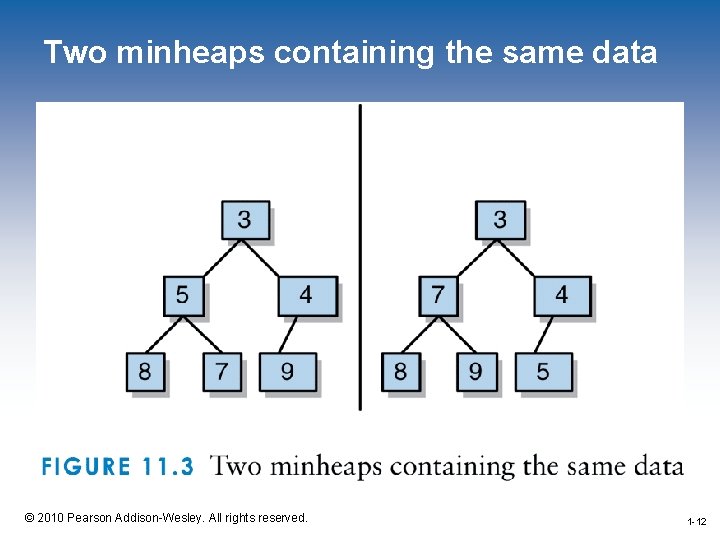
Heaps • A heap is a binary tree with two added properties: – It is a complete tree – For each node, the node is less than or equal to both the left child and the right child • This definition describes a minheap 1 -3 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -3

Heaps • In addition to the operations inherited from a binary tree, a heap has the following additional operations: – add. Element – remove. Min – find. Min 1 -4 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -4

The operations on a heap 1 -5 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -5

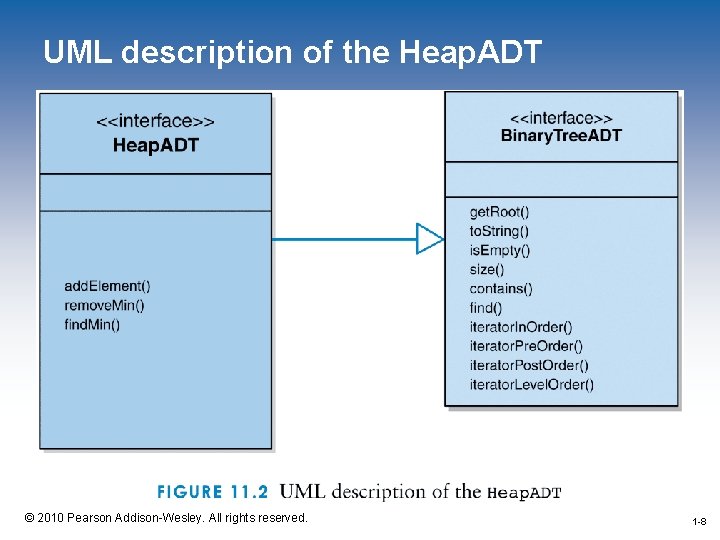
The Heap. ADT /** * Heap. ADT defines the interface to a Heap. * * @author Dr. Lewis * @author Dr. Chase * @version 1. 0, 9/9/2008 */ package jss 2; public interface Heap. ADT<T> extends Binary. Tree. ADT<T> { /** * Adds the specified object to this heap. * * @param obj the element to added to this head */ public void add. Element (T obj); 1 -6 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -6

The Heap. ADT (continued) /** * Removes element with the lowest value from this heap. * * @return the element with the lowest value from this heap */ public T remove. Min(); /** * Returns a reference to the element with the lowest value in * this heap. * * @return a reference to the element with the lowest value in this heap */ public T find. Min(); } 1 -7 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -7

UML description of the Heap. ADT 1 -8 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -8

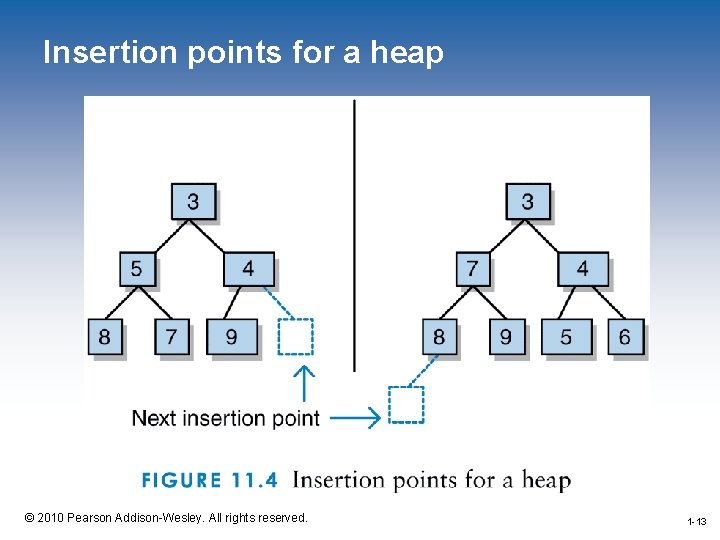
The add. Element Operation • The add. Element method adds a given element to the appropriate location in the heap • The proper location is the one location that will maintain the completeness of the tree 1 -9 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -9

The add. Element Operation • There is only one correct location for the insertion of a new node – Either the next open position from the left at level h – Or the first position in level h+1 if level h is full 1 -10 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -10

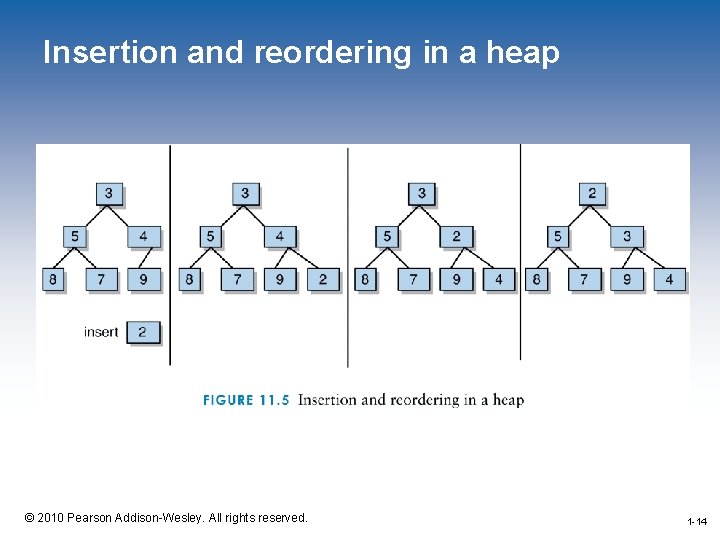
The add. Element Operation • Once we have located the new node in the proper position, then we must account for the ordering property • We simply compare the new node to its parent value and swap the values if necessary • We continue this process up the tree until either the new value is greater than its parent or the new value becomes the root of the heap 1 -11 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -11

Two minheaps containing the same data 1 -12 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -12

Insertion points for a heap 1 -13 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -13

Insertion and reordering in a heap 1 -14 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -14

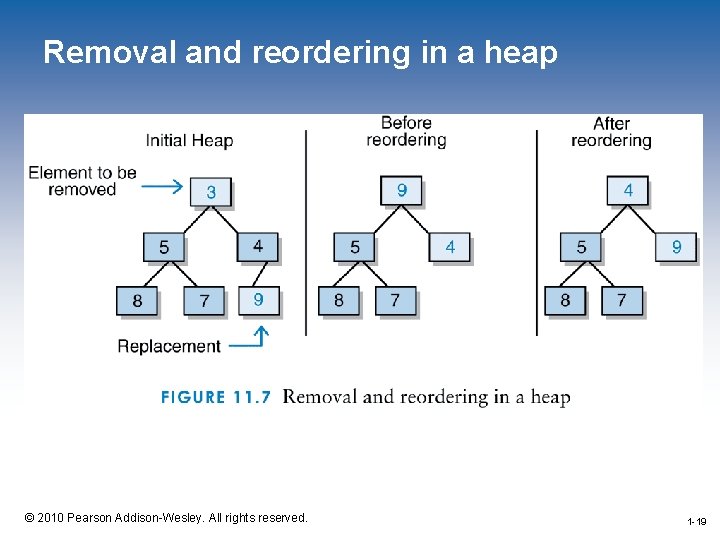
The remove. Min Operation • The remove. Min method removes the minimum element from the heap • The minimum element is always stored at the root • Thus we have to return the root element and replace it with another element 1 -15 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -15

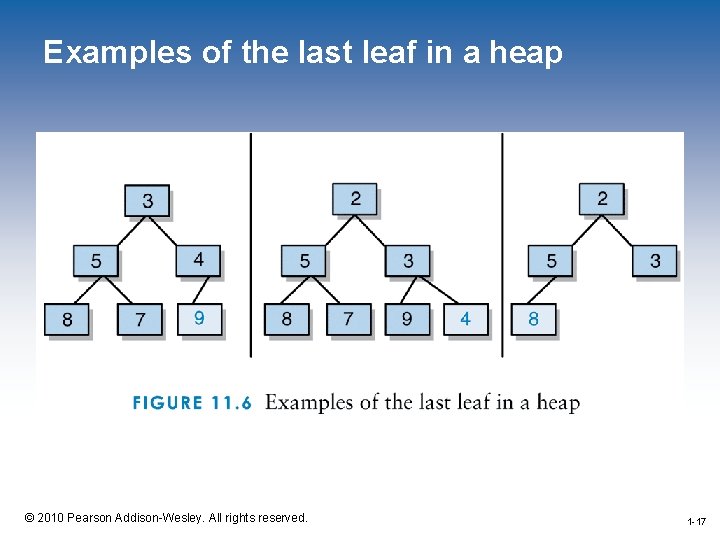
The remove. Min Operation • The replacement element is always the last leaf • The last leaf is always the last element at level h 1 -16 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -16

Examples of the last leaf in a heap 1 -17 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -17

The remove. Min Operation • Once the element stored in the last leaf has been moved to the root, the heap will have to reordered • This is accomplished by comparing the new root element to the smaller of its children and swapping them if necessary • This process is repeated down the tree until the element is either in a leaf or is less than both of its children 1 -18 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -18

Removal and reordering in a heap 1 -19 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -19

Using Heaps: Priority Queue • A priority queue is a collection that follows two ordering rules: – Items which have higher priority go first – Items with the same priority use a first in, first out method to determine their ordering • A priority queue could be implemented using a list of queues where each queue represents items of a given priority 1 -20 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -20

Using Heaps: Priority Queue • Another solution is to use a minheap • Sorting the heap by priority accomplishes the first ordering • However, the first in, first out ordering for items with the same priority has to be manipulated 1 -21 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -21

Using Heaps: Priority Queue • The solution is to create a Priority. Queue. Node object that stores the element to be placed on the queue, the priority of the element and the arrival order of the element • Then we simply define a compare. To method for the Priority. Queue. Node class that first compares priority then arrival time • The Priority. Queue class then extends the Heap class and stores Priority. Queue. Nodes 1 -22 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -22

The Priority. Queue. Node class /** * Priority. Queue. Node represents a node in a priority queue containing a * comparable object, order, and a priority value. * * @author Dr. Lewis * @author Dr. Chase * @version 1. 0, 8/19/08 */ public class Priority. Queue. Node<T> implements Comparable<Priority. Queue. Node> { private static int nextorder = 0; private int priority; private int order; private T element; /** * Creates a new Priority. Queue. Node with the specified data. * * @param obj the element of the new priority queue node * @param prio the integer priority of the new queue node */ 1 -23 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -23

The Priority. Queue. Node class (cont. ) public Priority. Queue. Node (T obj, int prio) { element = obj; priority = prio; order = nextorder; nextorder++; } /** * Returns the element in this node. * * @return the element contained within this node */ public T get. Element() { return element; } /** * Returns the priority value for this node. * * @return the integer priority for this node */ © 2010 Pearson Addison-Wesley. All rights reserved. 1 -24

The Priority. Queue. Node class (cont. ) public int get. Priority() { return priority; } /** * Returns the order for this node. * * @return the integer order for this node */ public int get. Order() { return order; } /** * Returns a string representation for this node. * */ public String to. String() { String temp = (element. to. String() + priority + order); return temp; } © 2010 Pearson Addison-Wesley. All rights reserved. 1 -25

The Priority. Queue. Node class (cont. ) /** * Returns the 1 if the current node has higher priority than * the given node and -1 otherwise. * * @param obj the node to compare to this node * @return the integer result of the comparison of the obj node and this * this one */ public int compare. To(Priority. Queue. Node obj) { int result; Priority. Queue. Node<T> temp = obj; if (priority > temp. get. Priority()) result = 1; else if (priority < temp. get. Priority()) result = -1; else if (order > temp. get. Order()) result = 1; else result = -1; return result; } } © 2010 Pearson Addison-Wesley. All rights reserved. 1 -26

The Priority. Queue class /** * Priority. Queue demonstrates a priority queue using a Heap. * * @author Dr. Lewis * @author Dr. Chase * @version 1. 0, 8/19/08 */ import jss 2. *; public class Priority. Queue<T> extends Array. Heap<Priority. Queue. Node<T>> { /** * Creates an empty priority queue. */ public Priority. Queue() { super(); } 1 -27 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -27

The Priority. Queue class (continued) /** * Adds the given element to this Priority. Queue. * * @param object the element to be added to the priority queue * @param priority the integer priority of the element to be added */ public void add. Element (T object, int priority) { Priority. Queue. Node<T> node = new Priority. Queue. Node<T> (object, priority); super. add. Element(node); } /** * Removes the next highest priority element from this priority * queue and returns a reference to it. * * @return a reference to the next highest priority element in this queue */ public T remove. Next() { Priority. Queue. Node<T> temp = (Priority. Queue. Node<T>)super. remove. Min(); return temp. get. Element(); } } © 2010 Pearson Addison-Wesley. All rights reserved. 1 -28

Implementing Heaps with Links • A linked implementation of a minheap would simply be an extension of our Linked. Binary. Tree class • However, since we need each node to have a parent pointer, we will create a Heap. Node class to extend our Binary. Tree. Node class we used earlier 1 -29 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -29

The Heap. Node class /** * Heap. Node creates a binary tree node with a parent pointer for use * in heaps. * * @author Dr. Lewis * @author Dr. Chase * @version 1. 0, 9/9/2008 */ package jss 2; public class Heap. Node<T> extends Binary. Tree. Node<T> { protected Heap. Node<T> parent; /** * Creates a new heap node with the specified data. * * @param obj the data to be contained within the new heap nodes */ Heap. Node (T obj) { super(obj); parent = null; } } © 2010 Pearson Addison-Wesley. All rights reserved. 1 -30

Implementing Heaps with Links • The add. Element method must accomplish three tasks: – Add the new node at the appropriate location – Reorder the heap – Reset the last. Node pointer to point to the new last node 1 -31 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -31

Linked. Heap /** * Heap implements a heap. * * @author Dr. Lewis * @author Dr. Chase * @version 1. 0, 9/9/2008 */ package jss 2; import jss 2. exceptions. *; public class Linked. Heap<T> extends Linked. Binary. Tree<T> implements Heap. ADT<T> { public Heap. Node<T> last. Node; public Linked. Heap() { super(); } 1 -32 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -32

Linked. Heap - add. Element /** * Adds the specified element to this heap in the appropriate * position according to its key value. Note that equal elements * are added to the right. * * @param obj the element to be added to this head */ public void add. Element (T obj) { Heap. Node<T> node = new Heap. Node<T>(obj); if (root == null) root=node; else { Heap. Node<T> next_parent = get. Next. Parent. Add(); if (next_parent. left == null) next_parent. left = node; else next_parent. right = node; node. parent = next_parent; } last. Node = node; count++; if (count>1) heapify. Add(); } © 2010 Pearson Addison-Wesley. All rights reserved. 1 -33

Linked. Heap - the add. Element Operation • The add. Element operation makes use of two private methods: – get. Next. Parent. Add that returns a reference to the node that will be the parent of the new node – heapify. Add that reorders the heap after the insertion 1 -34 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -34

Linked. Heap - get. Next. Parent. Add /** * Returns the node that will be the parent of the new node * * @return the node that will be a parent of the new node */ private Heap. Node<T> get. Next. Parent. Add() { Heap. Node<T> result = last. Node; while ((result != root) && (result. parent. left != result)) result = result. parent; if (result != root) if (result. parent. right == null) result = result. parent; else { result = (Heap. Node<T>)result. parent. right; while (result. left != null) result = (Heap. Node<T>)result. left; } else while (result. left != null) result = (Heap. Node<T>)result. left; return result; } © 2010 Pearson Addison-Wesley. All rights reserved. 1 -35

Linked. Heap - heapify. Add /** * Reorders this heap after adding a node. */ private void heapify. Add() { T temp; Heap. Node<T> next = last. Node; temp = next. element; while ((next != root) && (((Comparable)temp). compare. To (next. parent. element) < 0)) { next. element = next. parent. element; next = next. parent; } next. element = temp; } 1 -36 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -36

Linked. Heap - the remove. Min Operation • The remove. Min operation must accomplish three tasks: – Replace the element stored in the root with the element stored in the last leaf – Reorder the heap if necessary – Return the original root element 1 -37 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -37

Linked. Heap - remove. Min /** * Remove the element with the lowest value in this heap and * returns a reference to it. Throws an Empty. Collection. Exception * if the heap is empty. * * @return the element with the lowest value in * this heap * @throws Empty. Collection. Exception if an empty collection exception occurs */ public T remove. Min() throws Empty. Collection. Exception { if (is. Empty()) throw new Empty. Collection. Exception ("Empty Heap"); T min. Element = root. element; if (count == 1) { root = null; last. Node = null; } else { © 2010 Pearson Addison-Wesley. All rights reserved. 1 -38

Linked. Heap – remove. Min (cont. ) Heap. Node<T> next_last = get. New. Last. Node(); if (last. Node. parent. left == last. Node) last. Node. parent. left = null; else last. Node. parent. right = null; root. element = last. Node. element; last. Node = next_last; heapify. Remove(); } count--; return min. Element; } 1 -39 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -39

Linked. Heap - the remove. Min Operation • Like the add. Element operation, the remove. Min operation makes use of two private methods – get. New. Last. Node that returns a reference to the new last node in the heap – heapify. Remove that reorders the heap after the removal 1 -40 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -40

Linked. Heap – get. New. Last. Node /** * Returns the node that will be the new last node after a remove. * * @return the node that willbe the new last node after a remove */ private Heap. Node<T> get. New. Last. Node() { Heap. Node<T> result = last. Node; while ((result != root) && (result. parent. left == result)) result = result. parent; if (result != root) result = (Heap. Node<T>)result. parent. left; while (result. right != null) result = (Heap. Node<T>)result. right; return result; } 1 -41 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -41

Linked. Heap – heapify. Remove /** * Reorders this heap after removing the root element. */ private void heapify. Remove() { T temp; Heap. Node<T> node = (Heap. Node<T>)root; Heap. Node<T> left = (Heap. Node<T>)node. left; Heap. Node<T> right = (Heap. Node<T>)node. right; Heap. Node<T> next; if ((left == null) && (right == null)) next = null; else if (left == null) next = right; else if (right == null) next = left; else if (((Comparable)left. element). compare. To(right. element) < 0) next = left; else next = right; © 2010 Pearson Addison-Wesley. All rights reserved. 1 -42

Linked. Heap – heapify. Remove (cont. ) temp = node. element; while ((next != null) && (((Comparable)next. element). compare. To (temp) < 0)) { node. element = next. element; node = next; left = (Heap. Node<T>)node. left; right = (Heap. Node<T>)node. right; if ((left == null) && (right == null)) next = null; else if (left == null) next = right; else if (right == null) next = left; else if (((Comparable)left. element). compare. To(right. element) < 0) next = left; else next = right; } node. element = temp; } © 2010 Pearson Addison-Wesley. All rights reserved. 1 -43

Implementing Heaps with Arrays • An array implementation of a heap may provide a simpler alternative • In an array implementation, the location of parent and child can always be calculated • Given that the root is in position 0, then for any given node stored in position n of the array, its left child is in position 2 n + 1 and its right child is in position 2(n+1) • This means that its parent is in position (n 1)/2 1 -44 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -44

Array. Heap /** * Array. Heap provides an array implementation of a minheap. * * @author Dr. Lewis * @author Dr. Chase * @version 1. 0, 9/9/2008 */ package jss 2; import jss 2. exceptions. *; public class Array. Heap<T> extends Array. Binary. Tree<T> implements Heap. ADT<T> { public Array. Heap() { super(); } 1 -45 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -45

Implementing Heaps with Arrays • Like the linked version, the add. Element operation for an array implementation of a heap must accomplish three tasks: – Add the new node, – Reorder the heap, – Increment the count by one • The Array. Heap version of this method only requires one private method, heapify. Add which reorders the heap after the insertion 1 -46 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -46

Array. Heap - add. Element /** * Adds the specified element to this heap in the appropriate * position according to its key value. Note that equal elements * are added to the right. * * @param obj the element to be added to this heap */ public void add. Element (T obj) { if (count==tree. length) expand. Capacity(); tree[count] =obj; count++; if (count>1) heapify. Add(); } 1 -47 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -47

Array. Heap - heapify. Add /** * Reorders this heap to maintain the ordering property after * adding a node. */ private void heapify. Add() { T temp; int next = count - 1; temp = tree[next]; while ((next != 0) && (((Comparable)temp). compare. To (tree[(next-1)/2]) < 0)) { tree[next] = tree[(next-1)/2]; next = (next-1)/2; } tree[next] = temp; } 1 -48 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -48

Array. Heap - the remove. Min Operation • The remove. Min operation must accomplish three tasks: – Replace the element stored at the root with the element stored in the last leaf – Reorder the heap as necessary – Return the original root element • Like the add. Element operation, the remove. Min operation makes use of a private method, heapify. Remove to reorder the heap 1 -49 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -49

Array. Heap - remove. Min /** * Remove the element with the lowest value in this heap and * returns a reference to it. Throws an Empty. Collection. Exception if * the heap is empty. * * @return a reference to the element with the * lowest value in this head * @throws Empty. Collection. Exception if an empty collection exception occurs */ public T remove. Min() throws Empty. Collection. Exception { if (is. Empty()) throw new Empty. Collection. Exception ("Empty Heap"); T min. Element = tree[0]; tree[0] = tree[count-1]; heapify. Remove(); count--; return min. Element; } 1 -50 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -50

Array. Heap - heapify. Remove /** * Reorders this heap to maintain the ordering property. */ private void heapify. Remove() { T temp; int node = 0; int left = 1; int right = 2; int next; if ((tree[left] == null) && (tree[right] == null)) next = count; else if (tree[left] == null) next = right; else if (tree[right] == null) next = left; else if (((Comparable)tree[left]). compare. To(tree[right]) < 0) next = left; else next = right; temp = tree[node]; © 2010 Pearson Addison-Wesley. All rights reserved. 1 -51

Array. Heap – heapify. Remove (cont. ) while ((next < count) && (((Comparable)tree[next]). compare. To (temp) < 0)) { tree[node] = tree[next]; node = next; left = 2*node+1; right = 2*(node+1); if ((tree[left] == null) && (tree[right] == null)) next = count; else if (tree[left] == null) next = right; else if (tree[right] == null) next = left; else if (((Comparable)tree[left]). compare. To(tree[right]) < 0) next = left; else next = right; } tree[node] = temp; } 1 -52 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -52

Analysis of Heap Implementations • The add. Element operation is O(log n) for both implementations • The remove. Min operation is O(log n) for both implementations • The find. Min operation is O(1) for both implementations 1 -53 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -53

Using Heaps: Heap Sort • Given the ordering property of a heap, it is natural to think of using a heap to sort a list of objects • One approach would be to simply add all of the objects to a heap and then remove them one at a time in ascending order 1 -54 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -54

Using Heaps: Heap Sort • Insertion into a heap is O(log n) for any given node and thus would be O(n log n) for n nodes to build the heap • However, it is also possible to build a heap in place using an array • Since we know the relative position of each parent and its children in the array, we simply start with the first non-leaf node in the array, compare it to its children and swap if necessary 1 -55 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -55

Using Heaps: Heap Sort • We then work backward in the array until we reach the root • Since at most, this will require us to make two comparisons for each non-leaf node, this approach is O(n) to build the heap 1 -56 © 2010 Pearson Addison-Wesley. All rights reserved. 1 -56