Chapter 11 Nonparametric Tests 11 1 The Sign

Chapter 11 Nonparametric Tests

§ 11. 1 The Sign Test

Sign Test for a Population Median A nonparametric test is a hypothesis test that does not require any specific conditions concerning the shape of the population or the value of any population parameters. The sign test is a nonparametric test that can be used to test a population median against a hypothesized value k. The sign test for a population median can be left tailed, right tailed, or two tailed. Left-tailed test: H 0: median k and Ha: median < k Right-tailed test: H 0: median k and Ha: median > k Two-tailed test: H 0: median = k and Ha: median k Larson & Farber, Elementary Statistics: Picturing the World, 3 e 3

Sign Test for a Population Median To use the sign test, each entry is compared with the hypothesized median. If the entry is below the median, a sign is assigned; if above the median, a + sign is assigned. Test Statistic for the Sign Test When n 25, the test statistic x for the sign test is the smaller number of + or signs. When n > 25, the test statistic for the sign test is where x is the smaller number of + or signs and n is the sample size, i. e. , the total number of + or signs. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 4

Sign Test for a Population Median Performing a Sign Test for a Population Median In Words In Symbols 1. State the claim. Identify the null and alternative hypotheses. State H 0 and Ha. 2. Specify the level of significance. Identify . 3. Determine the sample size n by assigning + signs and – signs to the sample data. n = total number of + and – signs 4. Determine the critical value. If n 25, use Table 8. If n > 25, use Table 4. Continued. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 5

Sign Test for a Population Median Performing a Sign Test for a Population Median In Words In Symbols 5. Calculate the test statistic. If n 25, use x. If n > 25, use 6. Make a decision to reject or fail to reject the null hypothesis. If x or z is in the rejection region, reject H 0. Otherwise, fail to reject H 0. 7. Interpret the decision in the context of the original claim. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 6

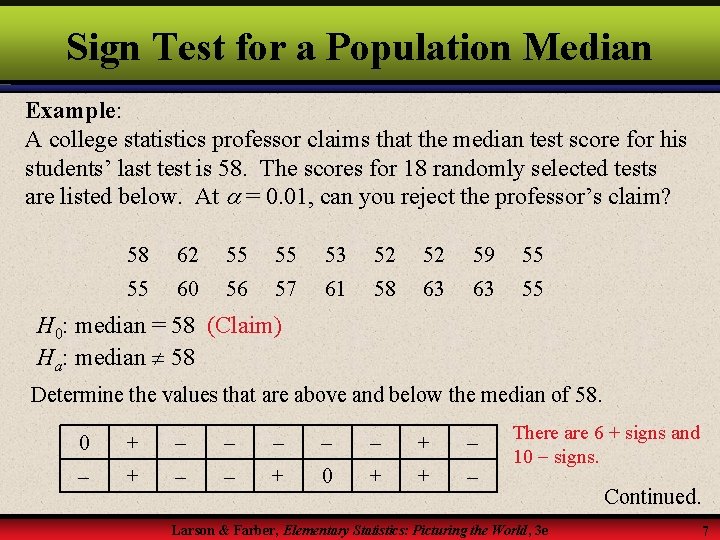
Sign Test for a Population Median Example: A college statistics professor claims that the median test score for his students’ last test is 58. The scores for 18 randomly selected tests are listed below. At = 0. 01, can you reject the professor’s claim? 58 62 55 55 53 52 52 59 55 55 60 56 57 61 58 63 63 55 H 0: median = 58 (Claim) Ha: median 58 Determine the values that are above and below the median of 58. 0 + + + 0 + + There are 6 + signs and 10 signs. Larson & Farber, Elementary Statistics: Picturing the World, 3 e Continued. 7

Sign Test for a Population Median Example continued: Since there are 6 + signs and 10 signs, n = 6 + 10 = 16. Using Table 8 with = 0. 01 (two tailed) and n = 16, the critical value is 2. Because n 25, the test statistic x is the smaller number of + signs or signs, so x = 6. 6 is greater than the critical value, so we fail to reject H 0. There is not enough evidence at the 1% level to reject the professor’s claim that the median test score is 58. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 8

The Paired-Sample Sign Test The paired-sample sign test is used to test the difference between two population medians when the populations are not normally distributed. For the paired-sample sign test to be used, the following must be true. 1. A sample must be randomly selected from each population. 2. The samples must be dependent (paired). The difference between corresponding data entries is found and the sign of the difference is recorded. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 9

The Paired-Sample Sign Test Performing a Paired-Sample Sign Test In Words In Symbols 1. Identify the claim. State the null and alternative hypotheses. State H 0 and Ha. 2. Specify the level of significance. Identify . 3. Determine the sample size n by finding the difference for each data pair. Assign a + sign for a positive difference, a – sign for a negative difference, and a 0 for no difference. n = total number of + and – signs Continued. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 10

The Paired-Sample Sign Test Performing a Paired-Sample Sign Test In Words In Symbols 4. Determine the critical value. Use Table 8 in Appendix B. 5. Find the test statistic. x = lesser number of + and – signs 6. Make a decision to reject or fail to reject the null hypothesis. If the test statistic is less than or equal to the critical value, reject H 0. Otherwise, fail to reject H 0. 7. Interpret the decision in the context of the original claim. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 11

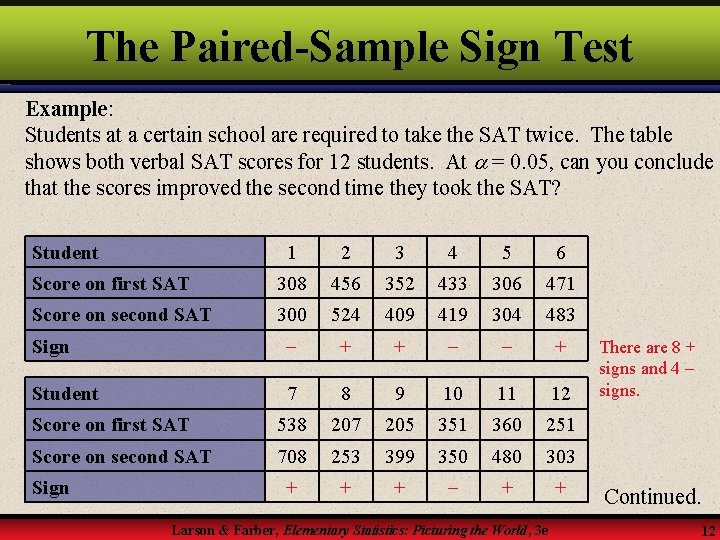
The Paired-Sample Sign Test Example: Students at a certain school are required to take the SAT twice. The table shows both verbal SAT scores for 12 students. At = 0. 05, can you conclude that the scores improved the second time they took the SAT? Student 1 2 3 4 5 6 Score on first SAT 308 456 352 433 306 471 Score on second SAT 300 524 409 419 304 483 Sign + + + Student 7 8 9 10 11 12 Score on first SAT 538 207 205 351 360 251 Score on second SAT 708 253 399 350 480 303 + + + Sign Larson & Farber, Elementary Statistics: Picturing the World, 3 e There are 8 + signs and 4 signs. Continued. 12

The Paired-Sample Sign Test Example continued: H 0: The SAT scores have not improved. Ha: The SAT scores have improved. (Claim) Since there are 8 + signs and 4 signs, n = 8 + 4 = 12. Using Table 8 with = 0. 05 (one tailed) and n = 12, the critical value is 2. The test statistic x is the smaller number of + signs or signs, so x = 4. 4 is greater than the critical value, so we fail to reject H 0. There is not enough evidence at the 5% level to support the claim that verbal SAT scores improved. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 13

§ 11. 2 The Wilcoxon Tests

The Wilcoxon Signed-Rank Test The Wilcoxon signed-rank test is a nonparametric test that can be used to determine whether two dependent samples were selected from populations having the same distribution. Performing a Wilcoxon Signed-Rank Test In Words In Symbols 1. Identify the claim. State the null and alternative hypotheses. State H 0 and Ha. 2. Specify the level of significance. Identify . 3. Determine the sample size n. Continued. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 15

The Wilcoxon Signed-Rank Test Performing a Wilcoxon Signed-Rank Test In Words In Symbols 4. Determine the critical value. 5. Calculate the test statistic ws. a. Complete a table with the following headers: b. Find the sum of the positive ranks and the sum of the negative ranks. Use Table 9 in Appendix B. Headers: Sample 1, Sample 2, Difference, Absolute value, Rank, and Signed rank. c. Select the smaller of absolute values of the sums. Continued. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 16

The Wilcoxon Signed-Rank Test Performing a Wilcoxon Signed-Rank Test In Words In Symbols 6. Make a decision to reject or fail to reject the null hypothesis. 7. Interpret the decision in the context of the original claim. If ws is less than or equal to the critical value, reject H 0. Otherwise, fail to reject H 0. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 17

The Wilcoxon Signed-Rank Test Example: A medical researcher want to determine whether a new drug affects the number of headache hours experienced by headache sufferers. To do so, he selects seven patients and asks each to give the number of headache hours (per day) each experiences before and after taking the drug. The results are shown in the table. At = 0. 05, can the researcher conclude that the new drug affects the number of hours? Patient Headache Hours (before) Headache Hours (after) 1 2 0. 8 2. 4 1. 6 1. 3 3 4 5 6 2. 8 2. 6 2. 7 0. 9 1. 6 1. 4 1. 5 1. 6 7 1. 2 1. 7 H 0: The drug does not affect the number of headache hours. Ha: The drug does affect the number of headache hours. (Claim) This is a two-tailed signed-rank test with = 0. 05 and n = 7. From Table 9, the critical value is 2. Continued. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 18

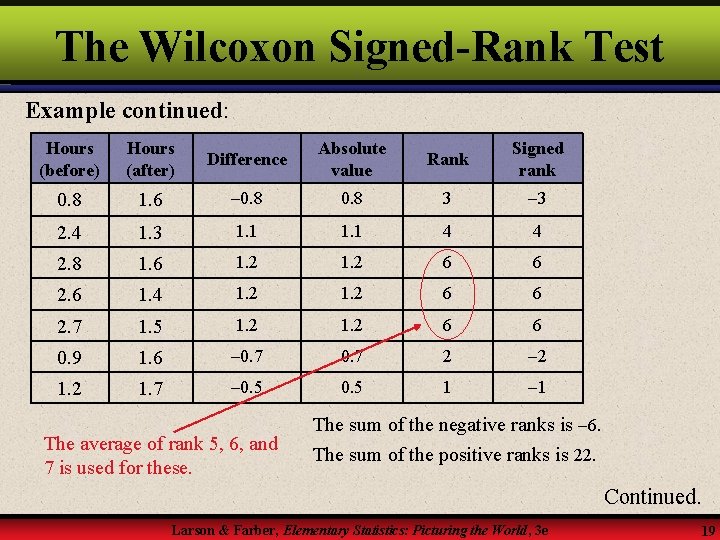
The Wilcoxon Signed-Rank Test Example continued: Hours (before) Hours (after) Difference Absolute value Rank Signed rank 0. 8 1. 6 0. 8 3 3 2. 4 1. 3 1. 1 4 4 2. 8 1. 6 1. 2 6 6 2. 6 1. 4 1. 2 6 6 2. 7 1. 5 1. 2 6 6 0. 9 1. 6 0. 7 2 2 1. 7 0. 5 1 1 The average of rank 5, 6, and 7 is used for these. The sum of the negative ranks is 6. The sum of the positive ranks is 22. Continued. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 19

The Wilcoxon Signed-Rank Test Example continued: The test statistic is the smaller of the absolute value of the two sums. | 6| = 6 |22| = 22 ws = 6 which is greater than the critical value of 2. Fail to reject H 0. There is not enough evidence at the 5% level to support the claim that the drug affects the number of headache hours. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 20

The Wilcoxon Rank Sum Test The Wilcoxon rank sum test is a nonparametric test that can be used to determine whether two independent samples were selected from populations having the same distribution. A requirement for the Wilcoxon rank sum test is that the sample size of both samples must be at least 10. n 1 represents the size of the smaller sample and n 2 represents the size of the larger sample. When calculating the sum of the ranks R, use the ranks for the smaller of the two samples. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 21

The Wilcoxon Rank Sum Test Statistic for the Wilcoxon Rank Sum Test Given two independent samples, the test statistic z for the Wilcoxon rank sum test is where R = sum of the ranks for the smaller sample, and Larson & Farber, Elementary Statistics: Picturing the World, 3 e 22

The Wilcoxon Rank Sum Test Performing a Wilcoxon Rank Sum Test In Words In Symbols 1. Identify the claim. State the null and alternative hypotheses. State H 0 and Ha. 2. Specify the level of significance. Identify . 3. Determine the critical value. Use Table 4 in Appendix B. 4. Determine the sample sizes. n 1 n 2 Continued. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 23

The Wilcoxon Rank Sum Test Performing a Wilcoxon Rank Sum Test In Words In Symbols 5. Find the sum of the ranks for the smaller sample. R a. List the combined data in ascending order. b. Rank the combined data. c. Add the sum of the ranks for the smaller sample. 6. Calculate the test statistic. Continued. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 24

The Wilcoxon Rank Sum Test Performing a Wilcoxon Rank Sum Test In Words In Symbols 7. Make a decision to reject or fail to reject the null hypothesis. 8. Interpret the decision in the context of the original claim. If z is in the rejection region, reject H 0. Otherwise, fail to reject H 0. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 25

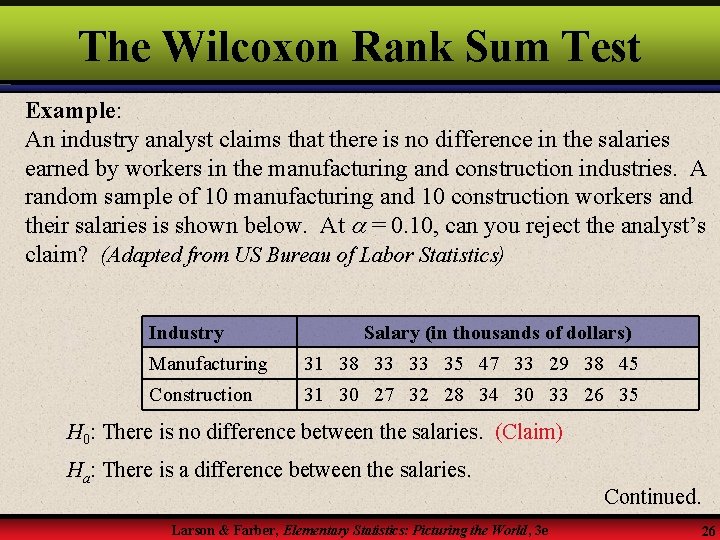
The Wilcoxon Rank Sum Test Example: An industry analyst claims that there is no difference in the salaries earned by workers in the manufacturing and construction industries. A random sample of 10 manufacturing and 10 construction workers and their salaries is shown below. At = 0. 10, can you reject the analyst’s claim? (Adapted from US Bureau of Labor Statistics) Industry Salary (in thousands of dollars) Manufacturing 31 38 33 33 35 47 33 29 38 45 Construction 31 30 27 32 28 34 30 33 26 35 H 0: There is no difference between the salaries. (Claim) Ha: There is a difference between the salaries. Larson & Farber, Elementary Statistics: Picturing the World, 3 e Continued. 26

The Wilcoxon Rank Sum Test Example continued: Because the test is a two-tailed test with = 0. 10, the critical values are z 0 = 1. 645 and z 0 = 1. 645. The rejection regions are z 1. 645 and z 1. 645. To find the values of R, μR, and R, construct a table that shows the combined data in ascending order and the corresponding ranks. Continued. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 27

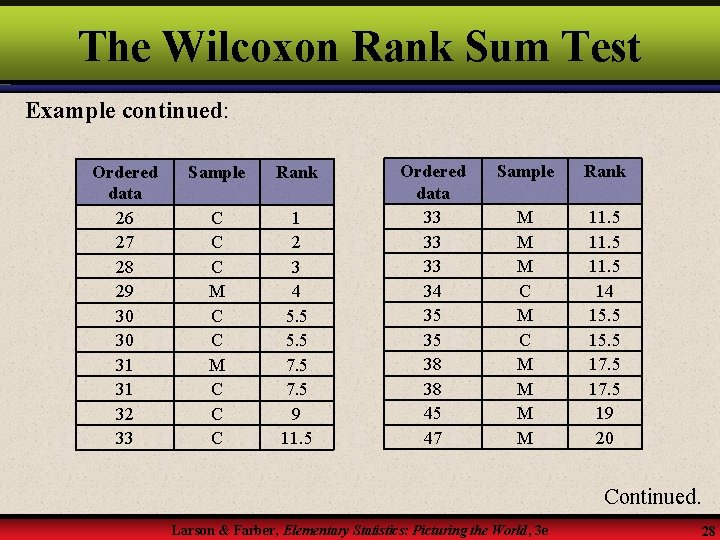
The Wilcoxon Rank Sum Test Example continued: Ordered data 26 27 28 29 30 30 31 31 32 33 Sample Rank C C C M C C C 1 2 3 4 5. 5 7. 5 9 11. 5 Ordered data 33 33 33 34 35 35 38 38 45 47 Sample Rank M M M C M M 11. 5 14 15. 5 17. 5 19 20 Continued. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 28

The Wilcoxon Rank Sum Test Example continued: Because the samples are the same size, n 1 can be associated with either sample. If we let n 1 be the sample of the construction workers, then R is the sum of the construction rankings. R = 1 + 2 + 3 + 5. 5 + 7. 5 + 9 + 11. 5 + 14 + 15. 5 = 74. 5 Using n 1 = 10 and n 2 = 10, we can find μR, and R. Continued. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 29

The Wilcoxon Rank Sum Test Example continued: When R = 74. 5, μR = 105 and R = 13. 23, the test statistic is Since 2. 31 is less than the critical value of 1. 645, H 0 is rejected. There is enough evidence at the 10% level to reject the claim that there is no difference in the salaries earned by workers in the manufacturing and construction industries. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 30

§ 11. 3 The Kruskal-Wallis Test

The Kruskal-Wallis Test The Kruskal-Wallis test is a nonparametric test that can be used to determine whether three or more independent samples were selected from populations having the same distribution. The null and alternative hypotheses for the Kruskal-Wallis test are as follows. H 0: There is no difference in the distribution of the populations. Ha: There is a difference in the distribution of the populations. Two conditions for using the Kruskal-Wallis test are that each sample must be randomly selected and the size of each sample must be at least 5. If these conditions are met, the test is approximated by a chi-square distribution with k – 1 degrees of freedom where k is the number of samples. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 32

The Kruskal-Wallis Test Statistic for the Kruskal-Wallis Test Given three or more independent samples, the test statistic H for the Kruskal-Wallis test is where k represent the number of samples, ni is the size of the ith sample, N is the sum of the sample sizes, and Ri is the sum of the ranks of the ith sample. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 33

The Kruskal-Wallis Test Performing a Kruskal-Wallis Test In Words In Symbols 1. Identify the claim. State the null and alternative hypotheses. State H 0 and Ha. 2. Specify the level of significance. Identify . 3. Identify the degrees of freedom d. f. = k – 1 4. Determine the critical value and the rejection region. Use Table 6 in Appendix B. Continued. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 34

The Kruskal-Wallis Test Performing a Kruskal-Wallis Test In Words In Symbols 5. Find the sum of the ranks for each sample. a. List the combined data in ascending order. b. Rank the combined data. 6. Calculate the test statistic. Continued. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 35

The Kruskal-Wallis Test Performing a Kruskal-Wallis Test In Words In Symbols 7. Make a decision to reject or fail to reject the null hypothesis. 8. Interpret the decision in the context of the original claim. If H is in the rejection region, reject H 0. Otherwise, fail to reject H 0. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 36

The Kruskal-Wallis Test Example: An insurance agent want to determine whethere is a difference in the annual premiums for home insurance in three states. He randomly selects homes from each state and records the annual premium for each state as shown below. At = 0. 05, can he conclude that the distributions of the annul premiums are different? State Annual Premium (in dollars) New Jersey 441 420 474 411 371 470 New York 753 684 869 719 1036 613 663 Pennsylvania 653 405 380 484 382 387 383 H 0: There is no difference in the premiums in the three states. Ha: There is a difference in the premiums in the three states. (Claim) Continued. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 37

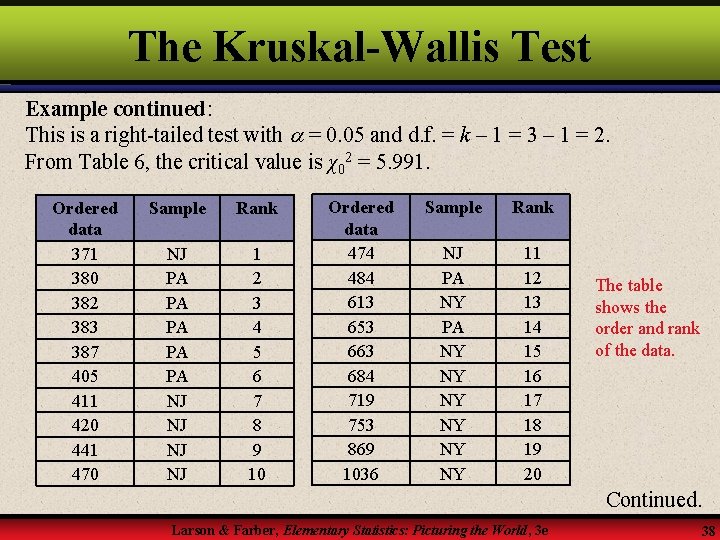
The Kruskal-Wallis Test Example continued: This is a right-tailed test with = 0. 05 and d. f. = k – 1 = 3 – 1 = 2. From Table 6, the critical value is χ02 = 5. 991. Ordered data 371 380 382 383 387 405 411 420 441 470 Sample Rank NJ PA PA PA NJ NJ 1 2 3 4 5 6 7 8 9 10 Ordered data 474 484 613 653 663 684 719 753 869 1036 Sample Rank NJ PA NY NY 11 12 13 14 15 16 17 18 19 20 The table shows the order and rank of the data. Continued. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 38

The Kruskal-Wallis Test Example continued: The sum of the ranks for each sample is as follows. R 1 = 1 + 7 + 8 + 9 + 10 + 11 = 46 R 2 = 13+ 15 + 16 +17 + 18 + 19 + 20 = 118 R 3 = 2 + 3 + 4 + 5 + 6 + 12 + 14 = 46 The test statistic is Because 12. 55 is greater than the critical value of 5. 991, reject H 0. There is enough evidence at the 5% level to support the claim that the annual premiums are different in the three states. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 39

§ 11. 4 Rank Correlation

The Spearman Rank Correlation Coefficient The Spearman rank correlation coefficient rs is a measure of the strength of the relationship between two variables. The Spearman rank correlation coefficient is calculated using the ranks of paired sample data entries. The formula for the Spearman rank correlation coefficient is where n is the number of paired data entries, and d is the difference between the ranks of a paired data entry. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 41

The Spearman Rank Correlation Coefficient The values of rs range from 1 to 1, inclusive. If the ranks of corresponding data pairs are identical, rs is equal to +1. If the ranks are in “reverse” order, rs is equal to 1. If there is no relationship, rs is equal to 0. To determine whether the correlation between variables is significant, you can perform a hypothesis test for the population correlation coefficient ρs. The null and alternative hypotheses for this test are as follows. H 0: ρs = 0 (There is no correlation between the variables. ) Ha: ρs 0 (There is a significant correlation between the variables. ) Larson & Farber, Elementary Statistics: Picturing the World, 3 e 42

The Spearman Rank Correlation Coefficient Testing the Significance of the Correlation Coefficient In Words In Symbols 1. State the null and alternative hypotheses. State H 0 and Ha. 2. Specify the level of significance. Identify . 3. Determine the critical value. Use Table 10 in Appendix B. Continued. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 43

The Spearman Rank Correlation Coefficient Testing the Significance of the Correlation Coefficient In Words In Symbols 4. Find the test statistic. 5. Make a decision to reject or fail to reject the null hypothesis. 6. Interpret the decision in the context of the original claim. If is greater than the critical value, reject H 0. Otherwise, fail to reject H 0. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 44

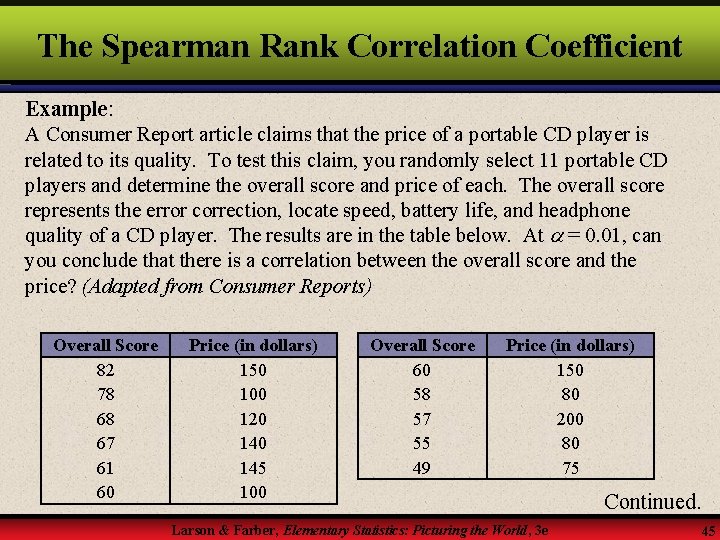
The Spearman Rank Correlation Coefficient Example: A Consumer Report article claims that the price of a portable CD player is related to its quality. To test this claim, you randomly select 11 portable CD players and determine the overall score and price of each. The overall score represents the error correction, locate speed, battery life, and headphone quality of a CD player. The results are in the table below. At = 0. 01, can you conclude that there is a correlation between the overall score and the price? (Adapted from Consumer Reports) Overall Score 82 78 68 67 61 60 Price (in dollars) 150 100 120 145 100 Overall Score 60 58 57 55 49 Price (in dollars) 150 80 200 80 75 Larson & Farber, Elementary Statistics: Picturing the World, 3 e Continued. 45

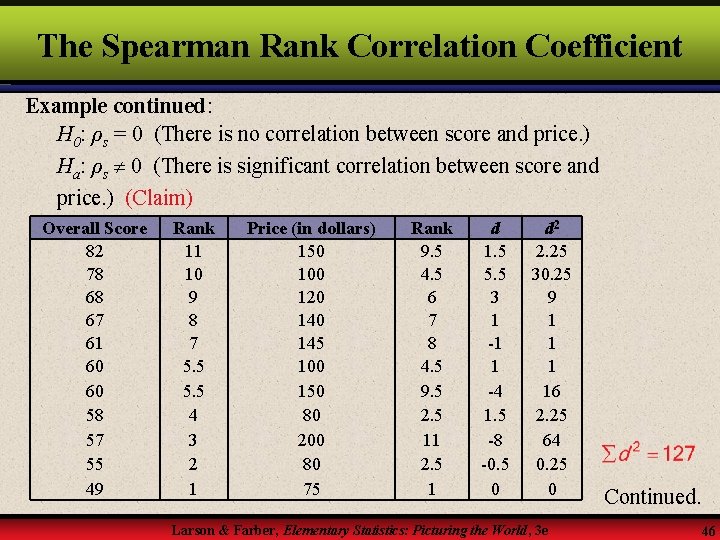
The Spearman Rank Correlation Coefficient Example continued: H 0: ρs = 0 (There is no correlation between score and price. ) Ha: ρs 0 (There is significant correlation between score and price. ) (Claim) Overall Score 82 78 68 67 61 60 60 58 57 55 49 Rank 11 10 9 8 7 5. 5 4 3 2 1 Price (in dollars) 150 100 120 145 100 150 80 200 80 75 Rank 9. 5 4. 5 6 7 8 4. 5 9. 5 2. 5 11 2. 5 1 d 1. 5 5. 5 3 1 -1 1 -4 1. 5 -8 -0. 5 0 d 2 2. 25 30. 25 9 1 16 2. 25 64 0. 25 0 Larson & Farber, Elementary Statistics: Picturing the World, 3 e Continued. 46

The Spearman Rank Correlation Coefficient Example continued: From Table 10 with = 0. 01 and n = 11, the critical value is 0. 818. When n = 11 and ∑d 2 = 127, the test statistic is Because 0. 423 < 0. 818, we fail to reject H 0. At the 1% level, there is not enough evidence to conclude that there is a significant correlation between the overall score of a CD player and its price. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 47

§ 11. 5 The Runs Test

The Runs Test for Randomness A run is a sequence of data having the same characteristic. Each run is preceded by and followed by data with a different characteristic or by no data at all. The number of data in a run is called the length of the run. Example: The gender of babies born in a hospital in one month was recorded in order of birth, where F represents a female and M represents a male. Determine the number of runs and the length of each run. FFFMMFFMFMMMFFFMMMM There are 8 runs. Length of F F F runs: 3 MM FF 2 2 M F 1 1 MMM FFF MMMM 3 3 4 Larson & Farber, Elementary Statistics: Picturing the World, 3 e 49

The Runs Test for Randomness The runs test for randomness is a nonparametric test that can be used to determine whether a sequence of sample data is random. Test Statistic for the Runs Test When n 1 20 and n 2 20, the test statistic for the runs test is G, the number of runs. When n 1 > 20 or n 2 > 20, the test statistic for the runs test is where Larson & Farber, Elementary Statistics: Picturing the World, 3 e 50

The Runs Test for Randomness Performing a Runs Test for Randomness In Words In Symbols 1. Identify the claim. State the null and alternative hypotheses. State H 0 and Ha. 2. Specify the level of significance. (Use = 0. 05 for the runs test. ) Identify . 3. Determine the number of data that have each characteristic and the number of runs. Determine n 1, n 2, and G. 4. Determine the critical value. If n 1 20 and n 2 20, use Table 12. If n 1 > 20 or n 2 > 20, use Table 4. Continued. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 51

The Runs Test for Randomness Performing a Runs Test for Randomness In Words In Symbols 5. Calculate the test statistic. If n 1 20 and n 2 20, use G. If n 1 > 20 or n 2 > 20, use 6. Make a decision to reject or fail to reject the null hypothesis. If G the lower critical value, or if G the upper critical value, reject H 0. Otherwise, fail to reject H 0. 7. Interpret the decision in the context of the original claim. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 52

The Runs Test for Randomness Example: An English professor at Smithville College is usually late for class. Students in his morning class record whether he is late (L) or on time (T ) for class each day. The results are shown below. At = 0. 05, can you conclude that the sequence is not random? TTLTTLTTLTTTTTT LTTLTTLTLTTLTTTTTL H 0: The sequence of arrivals is random. Ha: The sequence of arrivals is not random. (Claim) n 1 = the number of Ts = 42 n 2 = the number of Ls = 16 G = the number runs = 32 Because n 1 > 20, use Table 4 to find the critical values of z 0 = 1. 96 and z 0 = 1. 96. Larson & Farber, Elementary Statistics: Picturing the World, 3 e Continued. 53

The Runs Test for Randomness Example continued: Find the test statistic by first calculating μG and G. Because 2. 61 > 1. 96, reject H 0. At the 5% level, there is enough evidence to support the claim that the sequence of arrivals is not random. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 54

The Runs Test for Randomness Example: Students in the English professor’s afternoon class also record whether he is late (L) or on time (T ) for class each day. The results are shown below. At = 0. 05, can you conclude that this sequence is not random? T T L L L T L L T T L L L L L T L L L H 0: The sequence of arrivals is random. Ha: The sequence of arrivals is not random. (Claim) n 1 = the number of Ts = 9 n 2 = the number of Ls = 20 G = the number runs = 12 Continued. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 55

The Runs Test for Randomness Example continued: Because n 1 20 and n 2 20, use Table 12 to find the lower critical value 8 and the upper critical value 18. The test statistic is the number of runs G = 12. Because 12 is between the critical values of 8 and 18, we fail to reject H 0. At the 5% level, there is not enough evidence to support the claim that the sequence of arrivals is not random. Larson & Farber, Elementary Statistics: Picturing the World, 3 e 56