Chapter 11 Multifactor Analysis of Variance TwoFactor ANOVA

Chapter 11 Multifactor Analysis of Variance

Two-Factor ANOVA Design (KIJ > 1) 1. Test for Interaction. If no interaction exists: 2. Test for Main Effects. If interaction does exist: 3. Test for Differences among Treatment Combinations.

ANOVA Two-Factor Definitions SSA = 2 T 2 I* / JK – 2 T 2** / IJK SSB = 2 T 2*J / IK – 2 T 2** / IJK SSTR= 2 T 2 IJ / K – 2 T 2** / IJK SSAB= SSTR – SSA – SSB SSTOT= 3 x 2 IJK – 2 T 2** / IJK SSE = SSTOT – SSTR Fundamental Identity K>1 SSTOT = SSA+SSB+SSAB+SSE Note: 2 = I J

ANOVA Two-Factor Definitions Mean Squares Due to A: MSA = SSA / I – 1 Mean Squares Due to B: MSB = SSB / J – 1 Mean Square Due to Interaction: MSAB = SSAB / (I – 1)(J – 1) Mean Square Error: MSE = SSE / IJ(K – 1)

Two-Factor ANOVA (KIJ > 1 & equal K) Test for Interaction Null Hypothesis H 0 AB: Interaction Effects = 0 Test Statistic: = MSAB / MSE Alternative Hypothesis: Ha. AB: Interaction Exists Reject Region (upper tailed) F , (I-1)(J-1), IJ(K-1)

Two-Factor ANOVA (KIJ > 1 & equal K) Test for Main Effects (Factor A) Null Hypothesis H 0 A: 1 A = 2 A = …= IA Test Statistic: = MSA / MSE Alternative Hypothesis: Ha. A: Differences Exist in Factor A Reject Region (upper tailed) F , I-1, IJ(K-1)

Two-Factor ANOVA (KIJ > 1 & equal K) Test for Main Effects (Factor B) Null Hypothesis H 0 B: 1 B = 2 B = …= JB Test Statistic: = MSB / MSE Alternative Hypothesis: Ha. B: Differences Exist in Factor B Reject Region (upper tailed) F , J-1, IJ(K-1)

Example ANOVA Two-Factor (equal K) A study is conducted to investigate the effect of temperature and humidity on the force required to separate an adhesive product from a plastic laminate. The experimenter is interested in (4) temperature levels and (2) humidity levels. Three measurements are taken at each of the IJ treatment combinations. Are there real differences in the average responses for these levels of factors at a level of significance of. 05? The summary data of the experiment follows: T 11 = 119 T 21 = 108 T 31 = 95 T 41 = 85 (lbs) T 12 = 99 T 22 = 83 T 32 = 73 T 42 = 60 (lbs) x 2 IJK = 22, 722

Tukey’s Multiple Comparisons with No Interaction on significant Main Effects A 1. Find Q , I, IJ(K-1) 2. Find w = Q MSE/(JK) 3. Order the I-means (A) from smallest to largest. Underscore all pairs that differ by less than w. Pairs not underscored correspond to significantly different levels of factor A. For significant Main Effects B 1. Replace I with J in Q’s 2 nd subscript. 2. Replace JK by IK in w. 3. Order the J-means (factor B).

Example: Tukey’s Multiple Comparisons with No Interaction on significant Main Effects The study to investigate the effect of temperature and humidity on the force required to separate an adhesive product from a plastic found no statistical evidence of interaction between temperature and humidity. Differences in mean values among temperature levels & differences in mean values among humidity levels were found to exist. Identify significant differences in levels for both factors at a level of significance of. 05.

Example: ANOVA 2 -Factor (equal K) with Interaction A study is conducted to investigate the effect of temperature and humidity on the force required to separate an adhesive product from a plastic laminate. The experimenter is interested in (4) temperature levels and (2) humidity levels. Three measurements are taken at each of the IJ treatment combinations. Are there real differences in the average responses for these levels of factors at a level of significance of. 05? Conduct this analysis under the assumption that the test for interaction found a significant interaction (difference in response) between levels of temperature and levels of humidity. The summary data of the experiment follows: T 11 = 119 T 21 = 108 T 31 = 95 T 41 = 85 (lbs) T 12 = 99 T 22 = 83 T 32 = 73 T 42 = 60 (lbs) x 2 IJK = 22, 722

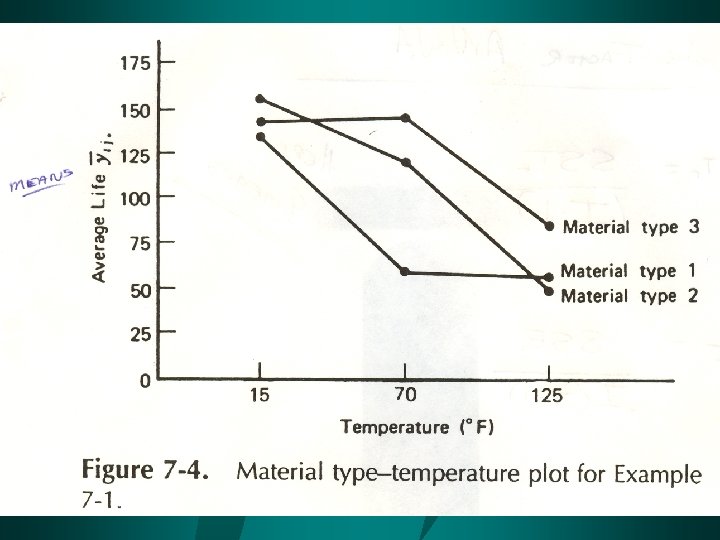
Example: ANOVA 2 -Factor (equal K) with Interaction You are designing a battery for use in a device that will be subjected to extreme variations in temperature. The only design parameter that you can select is the plate material. Three choices are available. You decide to test all three plate materials at (3) temperature levels that are consistent with the product end-use environment. Four batteries are tested at each combination of plate material and temperature. The resulting observed battery life data follows: Temperature (0 F) Material Type 1 2 3 15 T=539 T=623 T=576 70 T=229 T=479 T=583 125 T=230 (hrs) T=198 (hrs) T=342 (hrs) Test at =. 05 to determine if there is evidence to conclude that there are real differences in the battery life for these levels of temperature and material. Is there a choice of material that would give uniformly long life regardless of temperature? x 2 IJK =478, 546. 97

ANOVA Three-Factor Definitions SSA = 3 T 2 I**/ JKL – 3 T 2***/ IJKL SSAB= 3 T 2 IJ*/ KL – 3 T 2 I**/ JKL – 3 T 2*J*/ IKL + 3 T 2***/ IJKL SSABC= 3 T 2 IJK/L – 3 T 2 IJ*/KL – 3 T 2 I*K/ JL – 3 T 2*JK/ IL + 3 T 2*J*/IKL + 3 T 2 I**/JKL + 3 T 2**K/ IJL – 3 T 2***/IJKL SSTOT= 4 x 2 IJKL – 3 T 2***/ IJKL SSTOT= SSA+ SSB+ SSC+ SSAB + SSAC+ SSBC+ SSABC+ SSE Note: 3 = I J K 1 1 1

ANOVA Three-Factor Definitions Mean Squares Due to A: MSA = SSA / I – 1 Mean Square 2 -Factor Interaction: MSAB = SSAB / (I – 1)(J – 1) Mean Square 3 -Factor Interaction: MSABC = SSABC / (I – 1)(J – 1)(K-1) Mean Square Error: MSE = SSE / IJK(L – 1)

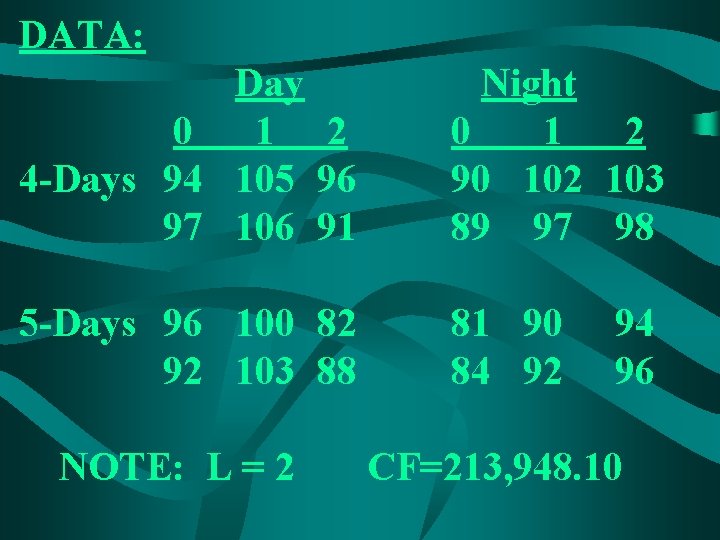
ANOVA - Three Factor An experiment is designed to investigate the effects of three factors on productivity (measured in thousands of dollars of items produced) per 40 -hour week at a manufacturing plant. The factors tested are: 1. Length of week (5 day-8 hrs or 4 day-10 hrs) 2. Shift (Day or Night) 3. Number of Breaks (0, 1, 2) The experiment was conducted over a 24 -week period. The data for this completely randomized design are shown on the next page. Perform an ANOVA at α =. 05.

DATA: Day 0 1 2 4 -Days 94 105 96 97 106 91 Night 0 1 2 90 102 103 89 97 98 5 -Days 96 100 82 92 103 88 81 90 84 92 NOTE: L = 2 CF=213, 948. 10 94 96

2 P Factorial Experiments > P = Number of Factors > 2 Levels per Factor (Low / High) > Complete Design = 2 P Combinations

22 Factorial Experiment A B > b > (1) ab a Mean (b+ab)/2 n ((1)+a)/2 n Mean (1)+b a+ab 2 n 2 n (1), a, b, and ab signify cell Totals.

Contrasts using Cells Totals A Contrast = ab + a – b – (1) B Contrast = ab –a + b – (1) AB Contrast = ab – a – b + (1) Main Effects ATotals = (A contrast) 2 P-1 n Main Effects BTotals = (B contrast) 2 P-1 n

Contrasts using Cell Means A Contrast = ab + a – b – (1) B Contrast = ab –a + b – (1) AB Contrast = ab – a – b + (1) Main Effects AMeans = (A contrast) 2 P-1 Main Effects BMeans = (B contrast) P-1 2

Signs for Contrasts in a 22 Factorial Treatment Factorial Effect Combination A B AB (1) a b ab – + – – + + + – – + Positive values to the treatment combinations that is at the High level. Negative values at the Lower level. Interactions by multiplying signs of the interacting factors.

Sum of Squares > 2 P Factorial (Totals) SSA = (A contrast)2 2 P n SSB = (B contrast)2 P 2 n 2 contrast) SSAB = (AB P 2 n SSE = SST – SSA – SSB – SSAB

Sum of Squares > 2 P Factorial (Means) SSA = n(A contrast)2 2 P 2 SSB = n(B contrast) 2 P SSAB = n(AB contrast)2 2 P

df for Mean Square >A=I– 1=1 >B=J– 1=1 >C=K– 1=1 >AB = (I-1)(J-1) = 1 >ABC = (I-1)(J-1)(K-1) = 1 P >Error = 2 (n-1)

Factorial Experiment Example A 23 factorial experiment was conducted to estimate the effects of three factors on the yield of a chemical reaction. The factors were A: catalyst concentration (high or low), B: reagent (std. or new), C: stirring rate (slow or fast). Three replicates were obtained for each treatment measured as a percent. Cell means are listed below. Calculate effects & test for each main effect and interaction at α = 0. 05. Treatment Cell Mean 1 69. 8733 a 78. 5500 b 77. 9067 ab 78. 1000 Treatment Cell Mean c 72. 4067 ac 76. 2733 bc 76. 1833 abc 75. 8333