Chapter 11 Interference and Diffraction A Power Point

$Chapter 11 - Interference and Diffraction A Power. Point Presentation by Mr. Shedge. S.$

The Superposition Principle • When two or more waves overlap, the resultant displacement at

Interference + + = = constructive interference waves in phase destructive interference waves ½

light as waves it works the same for light waves, sound waves, and *small*

x S 1 d S 2 Constructive interference. Path difference= 0, 2 /2 ,

S 1 d S 2 x D Path difference between two waves arriving at

Conditions for steady interference pattern 1. The two sources of light must be coherent

Measurement of wavelength by Biprism Experiment X= D/d

$Concept of Diffraction Types of diffraction 1. Fraunhofer diffraction 2. Fresnel diffraction$

$FRAUNHOFER DIFFRACTION DUE TO A SINGLE SLIT Diffraction due to a single slit Position$

RESOLUTION LIMIT Images are just resolved when central maximum of one pattern coincides with

Slides: 17

Download presentation

$Chapter 11 - Interference and Diffraction A Power. Point Presentation by Mr. Shedge. S.$

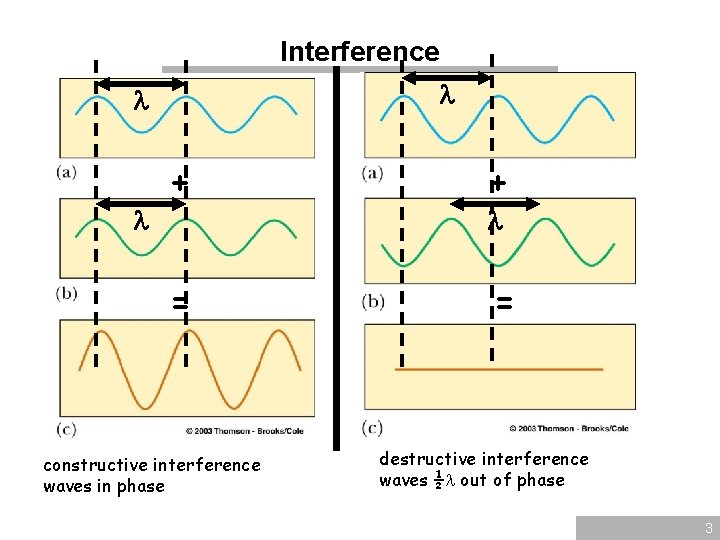
The Superposition Principle • When two or more waves overlap, the resultant displacement at any instant is equal to the vector sum of instantaneous displacements that would be produced at the point by the individual waves if each wave is present alone Constructive Interference Destructive Interference The superposition of two coherent light waves results in light and dark fringes on a screen. Interference of the waves on the surface of water

Interference + + = = constructive interference waves in phase destructive interference waves ½ out of phase 3

light as waves it works the same for light waves, sound waves, and *small* water waves 4

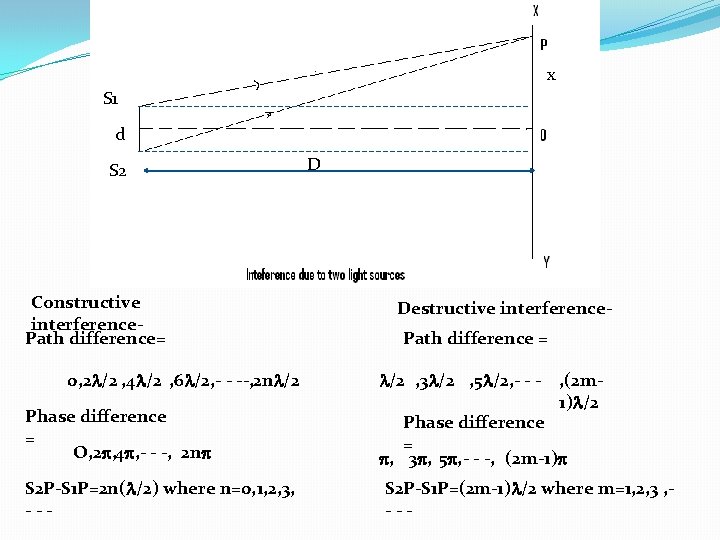
x S 1 d S 2 Constructive interference. Path difference= 0, 2 /2 , 4 /2 , 6 /2, - - --, 2 n /2 Phase difference = O, 2 , 4 , - - -, 2 n S 2 P-S 1 P=2 n( /2) where n=0, 1, 2, 3, --- D Destructive interference. Path difference = /2 , 3 /2 , 5 /2, - - - , (2 m 1) /2 Phase difference = , 3 , 5 , - - -, (2 m-1) S 2 P-S 1 P=(2 m-1) /2 where m=1, 2, 3 , ---

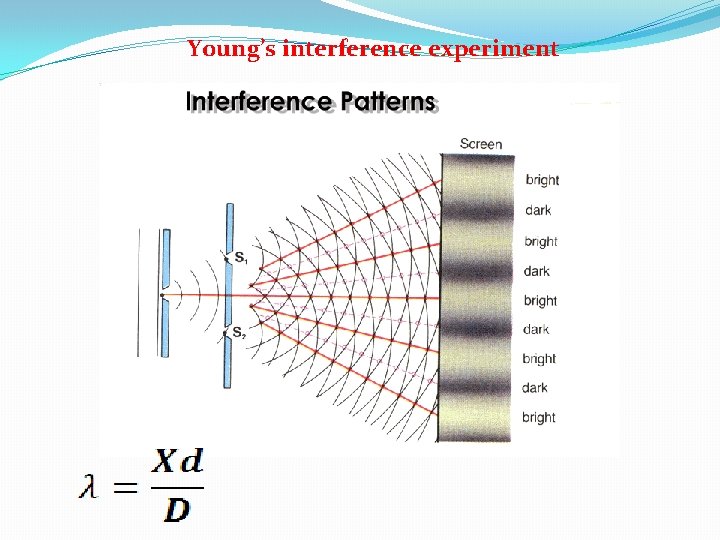
S 1 d S 2 x D Path difference between two waves arriving at a point P = S 2 P –S 1 P = xd/ D If path difference xd/D = nλ then we get nth bright also distance of nth bright from centre of screen = x = nλD/d. Also distance of (n+1)th bright from centre of screen = x = (n+1)λD/d. Now band width ( fringe width) X= x(n+1) –xn X= λ D /d

Conditions for steady interference pattern 1. The two sources of light must be coherent 2. The sources of light must be monochromatic 3. The two interfering waves must be in the same state of polarization 4. The two sources of light must emit light waves of equal amplitude or inten 5. The sources of light must be narrow 6. The separation between the two light sources should be as small as possibl 7. The distance of screen from the two sources should be large 8. The two interfering waves must travel in same direction

Young’s interference experiment

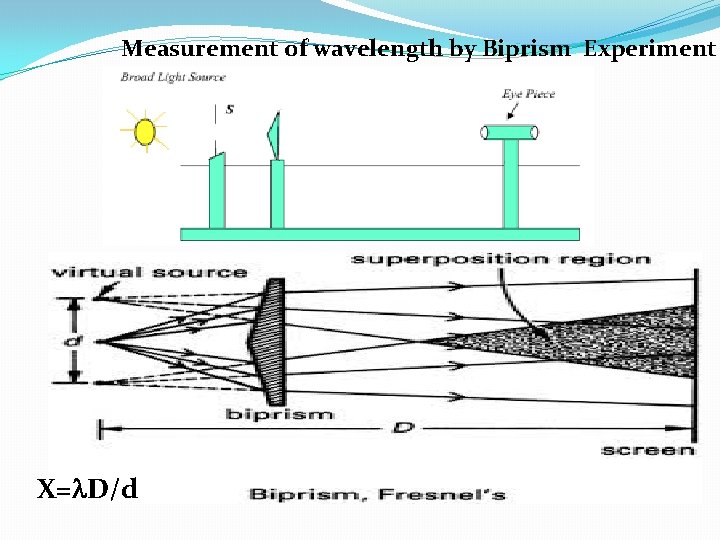
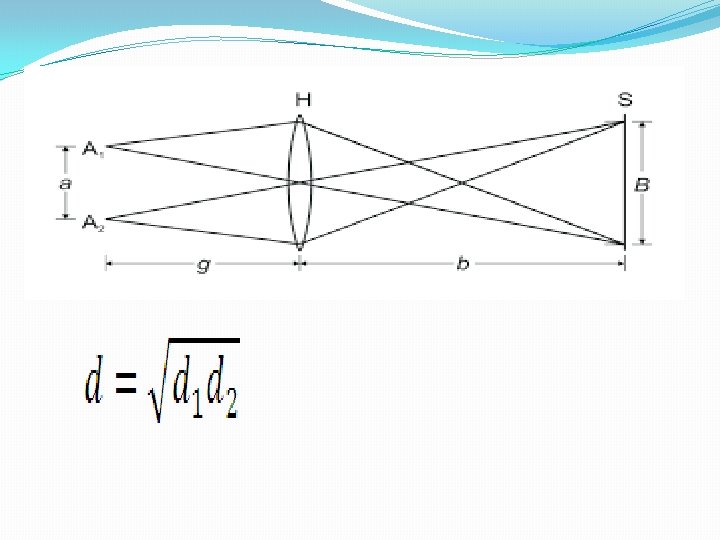
Measurement of wavelength by Biprism Experiment X= D/d

$Concept of Diffraction Types of diffraction 1. Fraunhofer diffraction 2. Fresnel diffraction$

Concept of Diffraction Types of diffraction 1. Fraunhofer diffraction 2. Fresnel diffraction

$FRAUNHOFER DIFFRACTION DUE TO A SINGLE SLIT Diffraction due to a single slit Position$

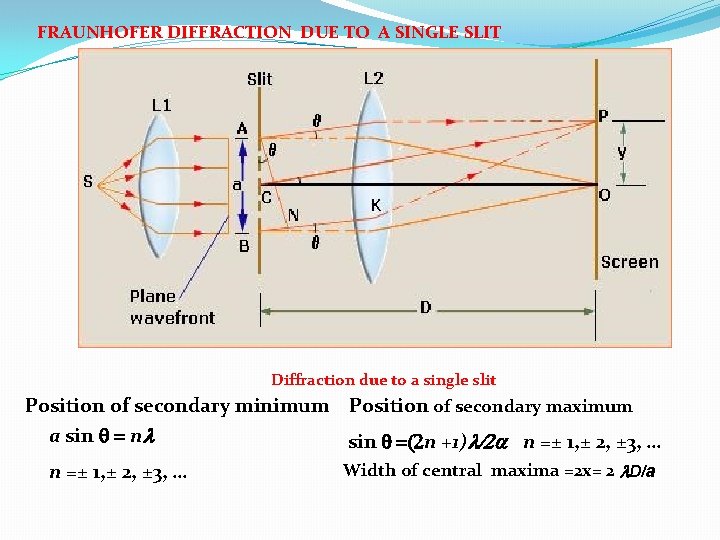
FRAUNHOFER DIFFRACTION DUE TO A SINGLE SLIT Diffraction due to a single slit Position of secondary minimum Position of secondary maximum a sin q = nl sin q =(2 n +1)l/2 a n =± 1, ± 2, ± 3, … Width of central maxima =2 x= 2 l. D/a n =± 1, ± 2, ± 3, …

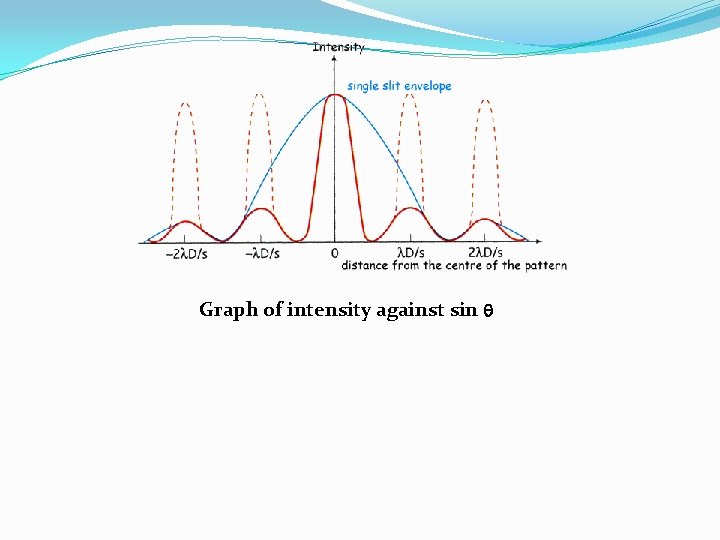
Graph of intensity against sin q

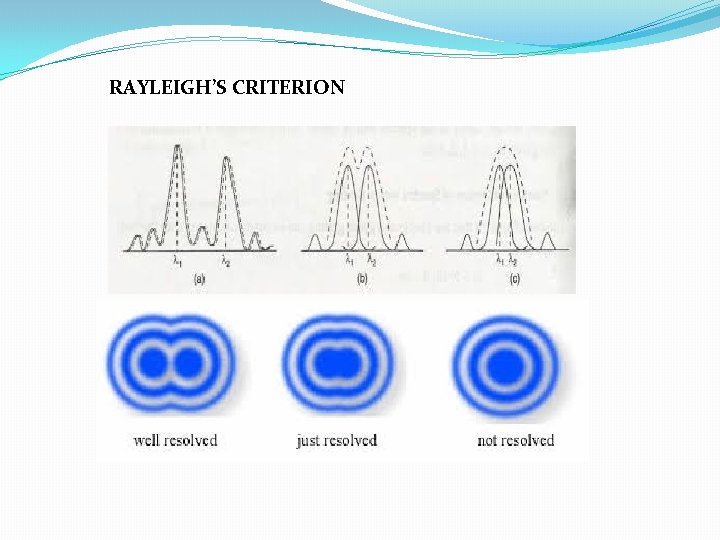
RAYLEIGH’S CRITERION

RESOLUTION LIMIT Images are just resolved when central maximum of one pattern coincides with first dark fringe of the other pattern. RESOLVING POWER OF MICROSCOPE RESOLVING POWER OF TELESCOPE

THANK TOU