CHAPTER 11 HETEROSCEDASTICITY What happens if the error







- Slides: 10

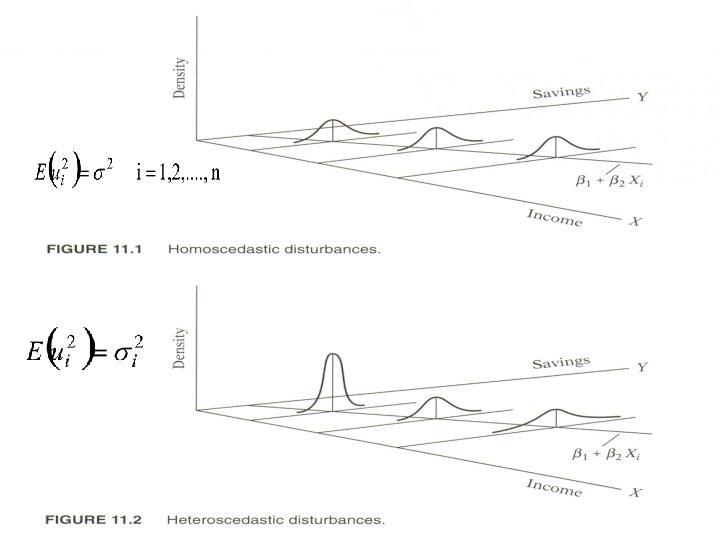
CHAPTER 11. HETEROSCEDASTICITY: What happens if the error variance is nonconstant?

Steps in Heteroscedasticity n What is the nature of heteroscedasticity? n What are its consequences? n How does one detect it? n What are the remedial measures?


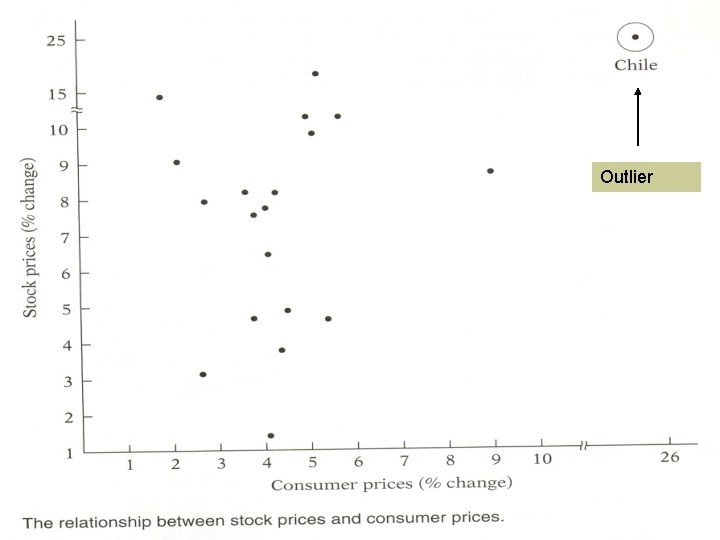
Reasons Behind Heteroscedasticity n Error-Learning models; i. e. Errors of behavior become smaller over time. n As incomes grow, people have more discretionary income and hence more scope for choice about the disposition of their income. Hence 2 i is likely to increase with income. n As data collection techniques improve, 2 i is likely to decrease. n Heteroscedasticity can also arise as a result of the presence of outliers. An outlier is an observation that is much different than the other observations in the sample.

Outlier

Reasons to be Continued n Another source of heteroscedasticity arises from violating Assumption 9 of CLRM, namely, that the regression model is not correctly specified. n Another source of heteroscedasticity is skewness in the distribution of one or more regressors in the model. i. e. It is well known that the distribution of income and wealth in most societies is uneven. n Incorrect data transformation n Incorrect functional form of regression analysis n Heteroscedasticity is more likely to happen in cross sectional data than time series data.

OLS Estimation Allowing for Heteroscedasticity n Larger confidence intervals for F and t values n Inaccurate results for F and t tests

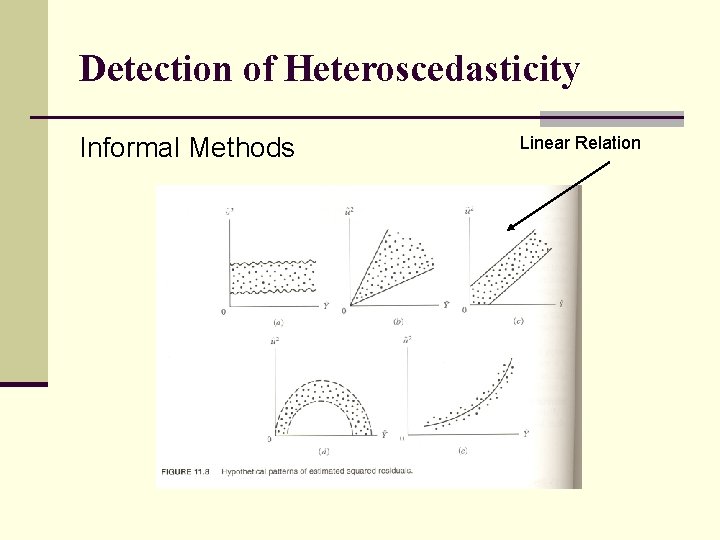
Detection of Heteroscedasticity Informal Methods Linear Relation

Formal Methods in Detecting Heteroscedasticity There are multiple econometric tests to detect the problem of heteroscedasticity such as: n n n Park Test Glejser Test Spearman’s Rank Correlation Test Goldfeld-Quandt Test Breusch-Pagan-Godfrey Test White’s General Heteroscedasticity Test

White’s test in More Details Null hypothesis: H 0: There is no Heteroscedasticity (where (n) times R 2 follows chi-square distribution Where 2= 3= 4= 5= 6= 0 is to represent Heteroscedasticity