Chapter 11 Gases Recall Properties of Gases Expand

Chapter 11 Gases

Recall: Properties of Gases • Expand to completely fill their container. • Take the shape of their container. • Low density. • Compressible. 2

Gas Particles Pushing • Gas molecules are constantly in motion. • As they move and strike a surface, they push on that surface. Ø Push = force. • Since pressure = force per unit area. Ø Gases can exert pressure 3

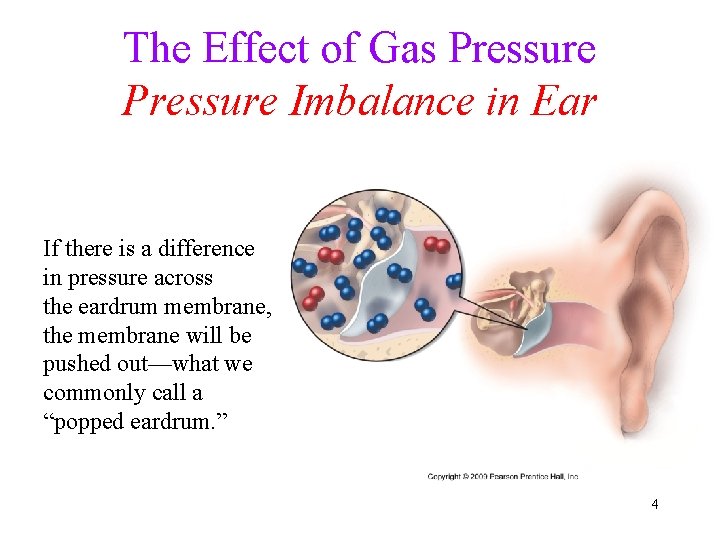
The Effect of Gas Pressure Imbalance in Ear If there is a difference in pressure across the eardrum membrane, the membrane will be pushed out—what we commonly call a “popped eardrum. ” 4

Measuring Air Pressure • Use a barometer. • Column of mercury supported by air pressure. • Force of the air on the surface of the mercury balanced by the pull of gravity on the column of mercury. Tro's Introductory Chemistry, Chapter 11 gravity 5

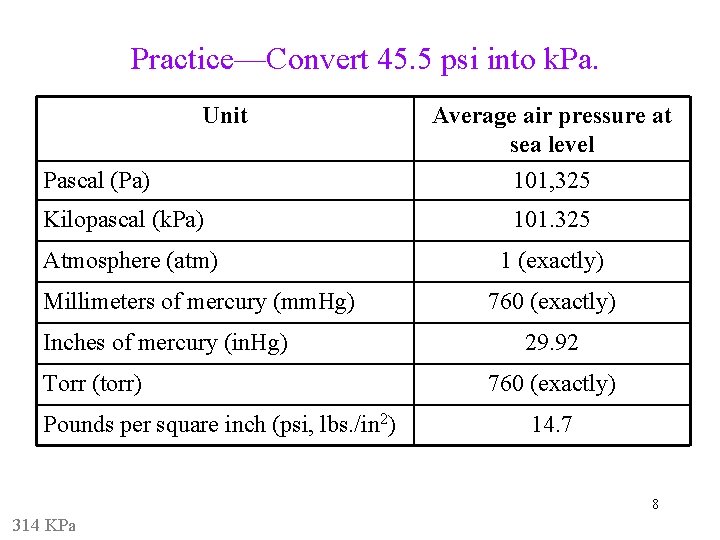
Common Units of Pressure Unit Average air pressure at sea level 101, 325 Pascal (Pa) Kilopascal (k. Pa) 101. 325 Atmosphere (atm) 1 (exactly) Millimeters of mercury (mm. Hg) Inches of mercury (in. Hg) Torr (torr) 760 (exactly) 29. 92 760 (exactly) Pounds per square inch (psi, lbs. /in 2) Tro's Introductory Chemistry, Chapter 11 14. 7 6

Example 11. 1—A High-Performance Bicycle Tire Has a Pressure of 125 psi. What Is the Pressure in mm. Hg? Given: 125 psi Find: mm. Hg Solution Map: psi Relationships: Solution: mm. Hg 14. 7 psi = 760 mm. Hg

Practice—Convert 45. 5 psi into k. Pa. Unit Pascal (Pa) Kilopascal (k. Pa) Atmosphere (atm) Millimeters of mercury (mm. Hg) Inches of mercury (in. Hg) Torr (torr) Pounds per square inch (psi, lbs. /in 2) Average air pressure at sea level 101, 325 101. 325 1 (exactly) 760 (exactly) 29. 92 760 (exactly) 14. 7 8 314 KPa

Gas Relationships The behavior of gases can be affected by • • Pressure Volume Temperature Amount of gas present Most of these parameters are inter-related

Boyle’s Law: Relationship Between Pressure and Volume • Pressure of a gas is inversely proportional to its volume. ØConstant T and amount of gas. • As P increases, V decreases by the same factor • P x V = constant. • P 1 x V 1 = P 2 x V 2 10

Example 11. 2—A Cylinder with a Movable Piston Has a Volume of 6. 0 L at 4. 0 atm. What Is the Volume at 1. 0 atm? Given: Find: V 1 =6. 0 L, P 1 = 4. 0 atm, P 2 = 1. 0 atm V 2, L Solution Map: V 1, P 2 Relationships: P 1 ∙ V 1 = P 2 ∙ V 2 Solution: Check: Since P and V are inversely proportional, when the pressure decreases ~4 x, the volume should increase ~4 x, and it does.

Practice—A Balloon Is Put in a Bell Jar and the Pressure Is Reduced from 782 torr to 0. 500 atm. If the Volume of the Balloon Is Now 2780 m. L, What Was It Originally? (1 atm = 760 torr) 1350 m. L 12

Relationship Between Pressure and Temperature • Raising the temperature increases the pressure. ØPressure is directly propotional to absolute temperature. ØMust occur at constant volume. ØAbsolute temperature is temperature in Kelvins 13

Charles’s Law: Relationship Between Volume and Temperature • Volume is directly proportional to absolute temperature. Ø Must occur at constant pressure • As T increases, V also increases. • Kelvin T = Celsius T + 273. 14

Example 11. 3—A Gas Has a Volume of 2. 57 L at 0 °C. What Was the Temperature at 2. 80 L? Given: V 1 =2. 80 L, V 2 = 2. 57 L, t 2 = 0°C Find: t 1, K and °C Solution Map: V 1, V 2, T 2 Relationships: T 1 T(K) = t(°C) + 273, Solution: Check: Since T and V are directly proportional, when the volume decreases, the temperature should decrease, and it does.

Practice—The Temperature Inside a Balloon Is Raised from 25. 0 °C to 250. 0 °C. If the Volume of Cold Air Was 10. 0 L, What Is the Volume of Hot Air? 17. 5 L 16

Avogadro’s Law • Volume is directly proportional to the number of gas molecules. ØV = constant x n. ØAs number of gas molecules increase, the volume increase • Count number of gas molecules by moles, n. 17

Example 11. 5—A 0. 22 Mol Sample of He Has a Volume of 4. 8 L. How Many Moles Must Be present to Give 6. 4 L? Given: Find: Solution Map: Relationships: Solution: V 1 =4. 8 L, V 2 = 6. 4 L, n 1 = 0. 22 mol n 2? V 1, V 2, n 1 n 2

Practice—If 1. 00 Mole of a Gas Occupies 22. 4 L, What Volume Would 0. 750 Moles Occupy? 16. 8 L 19

The Combined Gas Law • What if none of the parameters P, V, or T are constant? • Then the three gas relationships can all be combined to give the combine gas law. P 1 x V 1 = P 2 x V 2 20

Example 11. 4—A Sample of Gas Has an Initial Volume of 158 m. L at a Pressure of 735 mm. Hg and a Temperature of 34 °C. If the Gas Is Compressed to 108 m. L and Heated to 85 °C, What Is the Final Pressure? Given: V 1 = 158 m. L, t 1 = 34 °C L, P 1 = 735 mm. Hg V 2 = 108 m. L, t 2 = 85 °C Find: P 2, mm. Hg Solution Map: Relationships: Solution: P 1, V 2, T 1, T 2 T(K) = t(°C) + 273, P 2

Practice—A Gas Occupies 10. 0 L When Its Pressure Is 3. 00 atm and Temperature Is 27 °C. What Volume Will the Gas Occupy at a pressure of 1 atm and temperature of 30 °C ? Ans: 30. 3 L 22

Standard Conditions • Scientists have agreed on a set of conditions to report measurements so that comparison is easy. We call these standard conditions. • often referred to as STP ØSTP means standard temperature and pressure • standard pressure = 1 atm • standard temperature = 273 K Ø 0 °C 23

Ideal Gas Law • By combining the gas laws, we can write a general equation. • R is called the Gas Constant. • The value of R depends on the units of P and V. ØWe will use 0. 0821 V to L. and convert P to atm and 24

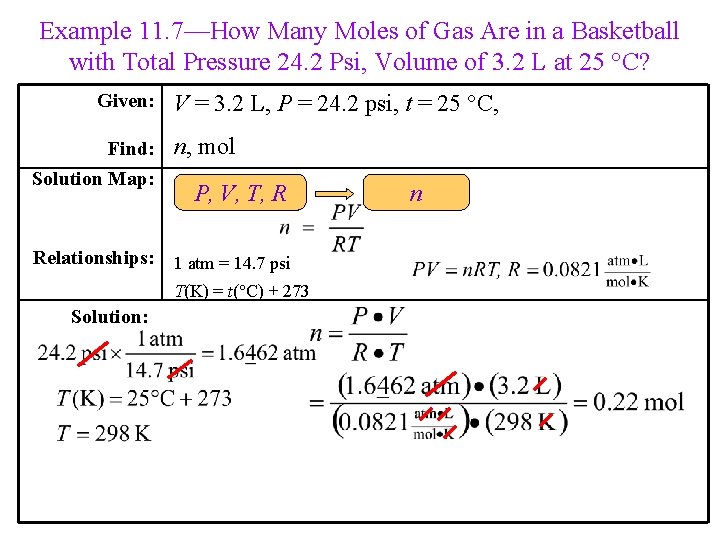
Example 11. 7—How Many Moles of Gas Are in a Basketball with Total Pressure 24. 2 Psi, Volume of 3. 2 L at 25 °C? Given: Find: Solution Map: V = 3. 2 L, P = 24. 2 psi, t = 25 °C, n, mol P, V, T, R Relationships: 1 atm = 14. 7 psi T(K) = t(°C) + 273 Solution: n

Practice—Calculate the Volume Occupied by 637 g of SO 2 (MM 64. 07) at 6. 08 x 103 mm. Hg and – 23 °C. 25. 5 L 26

Gas Density • Gas density can be determined from the ideal gas equation PV = n. RT • Based on this equation, the gas density is given as: • Density is directly proportional to molar mass. 27

**Example**—Calculate the Density of a Gas at 775 torr and 27 °C if 0. 250 moles Weighs 9. 988 g. 28

Practice 1—Identify the gas that has a mass of 12. 0 g and Occupies 197 L at 380 torr and 127 °C? 4. 0 g/mol 29

Practice 2—What is the molar mass of a gas that has a Mass 0. 311 g, a Volume of 0. 225 L at 55 °C and 886 mm. Hg. 31. 9 g/mol

Partial Pressure • Each gas in the mixture exerts a pressure independent of the other gases in the mixture. • The pressure of a component gas in a mixture is called a partial pressure. • The sum of the partial pressures of all the gases in a mixture equals the total pressure. ØDalton’s law of partial pressures. ØPtotal = Pgas A + Pgas B + Pgas C +. . . 31

Example 11. 9—A Mixture of He, Ne, and Ar Has a Total Pressure of 558 Mm. Hg. If the Partial Pressure of He Is 341 Mm. Hg and Ne Is 112 Mm. Hg, Determine the Partial Pressure of Ar in the Mixture. Given: PHe= 341 mm. Hg, PNe= 112 mm. Hg, Ptot = 558 mm. Hg Find: PAr, mm. Hg Solution Map: Ptot, PHe, PNe PAr = Ptot – (PHe + PNe) Relationships: Ptot = Pa + Pb + etc. Solution:

The Partial Pressure of Each Gas in a Mixture, or the Total Pressure of a Mixture, Can Be Calculated Using the Ideal Gas Law 33

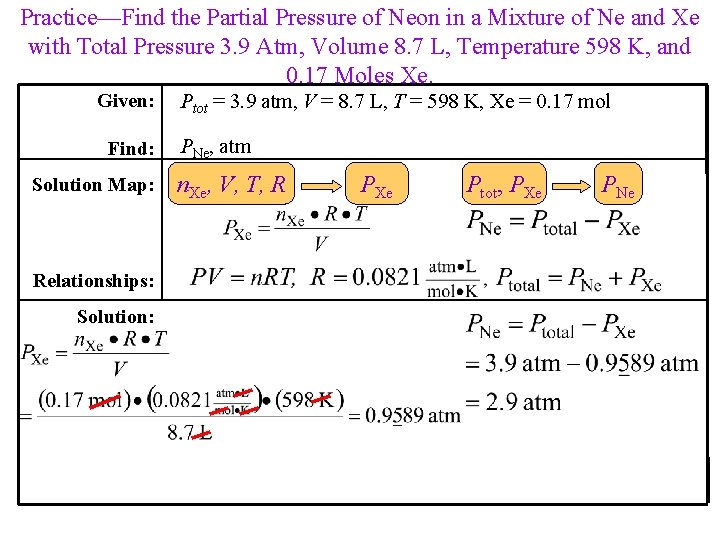
Practice—Find the Partial Pressure of Neon in a Mixture of Ne and Xe with Total Pressure 3. 9 Atm, Volume 8. 7 L, Temperature 598 K, and 0. 17 Moles Xe. Given: Find: Solution Map: Relationships: Solution: Ptot = 3. 9 atm, V = 8. 7 L, T = 598 K, Xe = 0. 17 mol PNe, atm n. Xe, V, T, R PXe Ptot, PXe PNe

Mountain Climbing and Partial Pressure • Our bodies are adapted to breathe O 2 at a partial pressure of 0. 21 atm. • Partial pressures of O 2—lower than 0. 1 atm—leads to hypoxia. Ø Unconsciousness or death. • Climbers of Mt. Everest must carry O 2 in cylinders to prevent hypoxia. 35

Deep Sea Divers and Partial Pressure • It is also possible to have too much O 2, a condition called oxygen toxicity. Ø PO 2 > 1. 4 atm. • When diving deep, the pressure of the air that divers breathe increases, so the partial pressure of the oxygen increases. Ø At a depth of 55 m, the partial pressure of O 2 is 1. 4 atm. Ø Divers that go below 50 m use a mixture of He and O 2 called heliox that contains a lower percentage of O 2 than air.

Collecting Gases • Gases are often collected over water. • The problem is that since water evaporates, there is also water vapor in the collected gas. • The partial pressure of the water vapor, called the vapor pressure, depends only on the temperature. 37

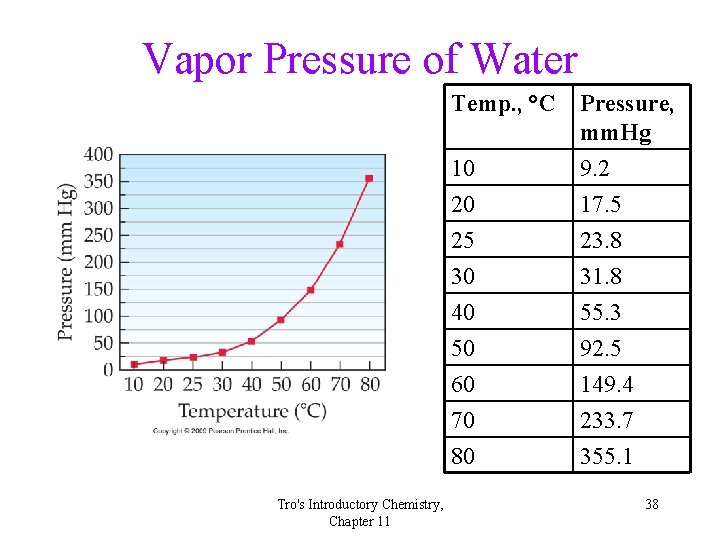
Vapor Pressure of Water Temp. , °C Tro's Introductory Chemistry, Chapter 11 10 20 Pressure, mm. Hg 9. 2 17. 5 25 30 40 50 60 70 80 23. 8 31. 8 55. 3 92. 5 149. 4 233. 7 355. 1 38

Practice— 0. 12 moles of H 2 Is Collected Over Water in a 10. 0 L Container at 323 K. Find the Total Pressure (Vapor Pressure of Water at 50 C = 92. 6 mm. Hg) Given: V = 10. 0 L, n. H 2 = 0. 12 mol, T = 323 K Find: Ptotal, atm Solution Map: n. H 2, V, T Relationships: Solution: PH 2 1 atm = 760 mm. Hg Ptotal = PA + PB, PH 2, PH 2 O Ptotal

Recommended Study Problems Chapter 11 NB: Study problems are used to check the student’s understanding of the lecture material. Students are EXPECTED TO BE ABLE TO SOLVE ALL THE SUGGESTED STUDY PROBLEMS. If you encounter any problems, please talk to your professor or seek help at the HACC-Gettysburg learning center. Questions from text book Chapter 11 7, 27, 33, 35, 37, 39, 43, 45, 49, 51, 53, 55, 57, 63, 65, 67, 79, 81, 83, 85, 87, 89, 93, 95, 97, 191, 127 ANSWERS -The answers to the odd-numbered study problems are found at the back of your textbook 40