Chapter 11 Failure Distribution Topics n n n

Chapter 11 Failure Distribution

Topics n n n n n Reliability Concept Design Life Mean time to failure (MTTF) Median time to failure, tmed Mode of the failure time, tmod Variance of the failure time Hazard Rate Function The bathtub curve Cumulative hazard function and average failure rate Conditional Reliability Danaipong Chetchotsak, Ph. D. 2

Concept of Reliability n n Def: Reliability, R(t) is defined as the probability that a piece of equipment will function over some time period t. Let T be a continuous random variable representing the time to failure or time between failure of the equipment, T≥ 0. Thus, Danaipong Chetchotsak, Ph. D. 3

Concept of Reliability (cont’d) n Let F(t) be the cumulative distribution function (CDF), where T is the time to failure and t is any time period Danaipong Chetchotsak, Ph. D. 4

Concept of Reliability (cont’d) n Let f(t) be the probability density function (PDF) of the time to failure t, then n and n Also, Danaipong Chetchotsak, Ph. D. 5
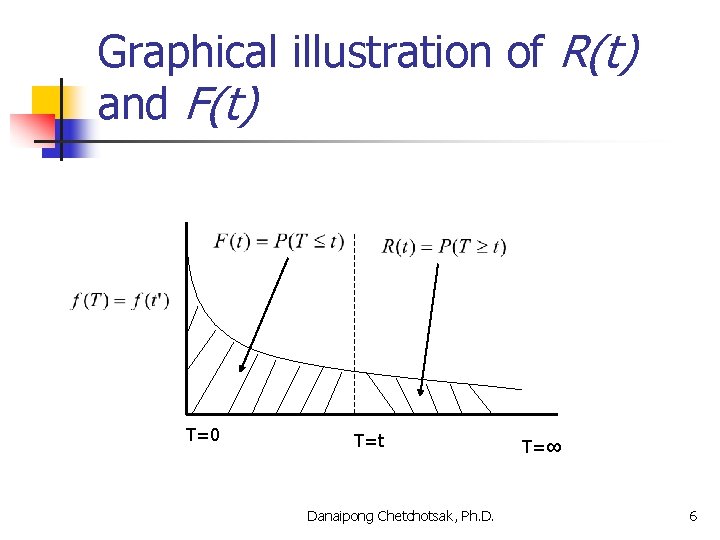
Graphical illustration of R(t) and F(t) T=0 T=t Danaipong Chetchotsak, Ph. D. T=∞ 6

Concept of Reliability (cont’d) n Note that n and, n Thus, Danaipong Chetchotsak, Ph. D. 7

Concept of Reliability (cont’d) n In summary, if f(t) is given, n If R(t) is given, where and Danaipong Chetchotsak, Ph. D. 8

Example 3. 1 n Given the probability density function (PDF) of the failure time for an air compressor below, what is the equipment’s reliability for a 100 -hour operating life? , Danaipong Chetchotsak, Ph. D. 9

Example 3. 2 n Given the cumulative distribution function (CDF) of the failure distribution for a piece of equipment below. , Danaipong Chetchotsak, Ph. D. in hours 10

Example 3. 2 (cont’d) n 1. 2. 3. 4. Answer the following questions. Find the probability that the equipment will fail by 500 hours. Find the probability that the equipment will fail between 500 -3, 000 hours. Find the probability that the equipment will last for more than 5, 000 hours. If there are 200 pieces of equipment in the facility, what is the average number of failures during the first 500 hours? Danaipong Chetchotsak, Ph. D. 11

Design Life n Design life is the time to failure that corresponds to a certain value of reliability or the desired reliability value. Danaipong Chetchotsak, Ph. D. 12

Example 3. 3 n Given that , n Find the design life if the acceptable reliability is 95%. Danaipong Chetchotsak, Ph. D. 13

Mean time to failure (MTTF) n Let f(t) be the probability density function for the time to failure t. The mean or MTTF of is defined as or Here, Danaipong Chetchotsak, Ph. D. 14

Median time to failure, tmed n The median time to failure is the failure time when in 50% of the failures occur before tmed and other 50% occur after tmed. Danaipong Chetchotsak, Ph. D. 15
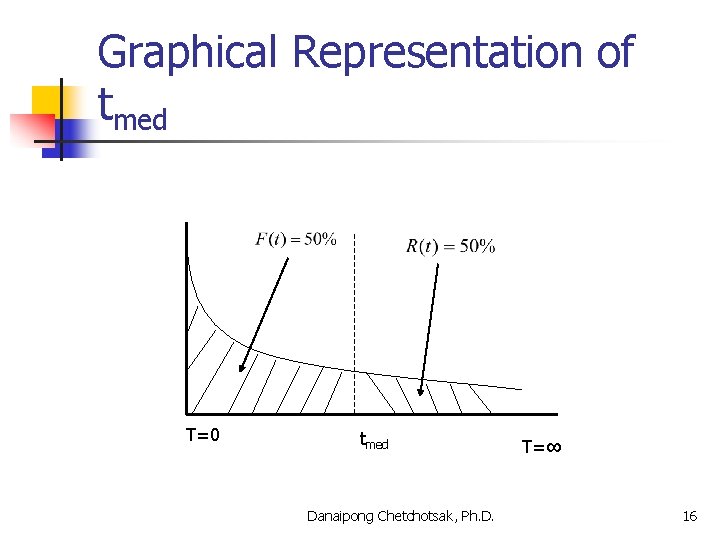
Graphical Representation of tmed T=0 tmed Danaipong Chetchotsak, Ph. D. T=∞ 16

Mode of the failure time, tmod n n The mode of the failure time is the most likely observed failure time or the time that most frequently occurs. Here tmod may be determined by solving the equation below Danaipong Chetchotsak, Ph. D. 17

Mode of the failure time, tmod (cont’d) n tmod is the time which n If t~normal, tmod=tmed=MTTF Danaipong Chetchotsak, Ph. D. 18

Variance of the failure time, 2 σ n If t and f(t) is the time to failure and is the corresponding probability density function, the variance of the failure time is computed as Danaipong Chetchotsak, Ph. D. 19

Example 3. 4 n The failure probability density function of a piece of equipment is defined as , n Find MTTF, tmed, and tmod Danaipong Chetchotsak, Ph. D. 20

Hazard Rate Function, λ n The simplest definition: n n The unit is failures per unit of time A more general definition: Danaipong Chetchotsak, Ph. D. 21
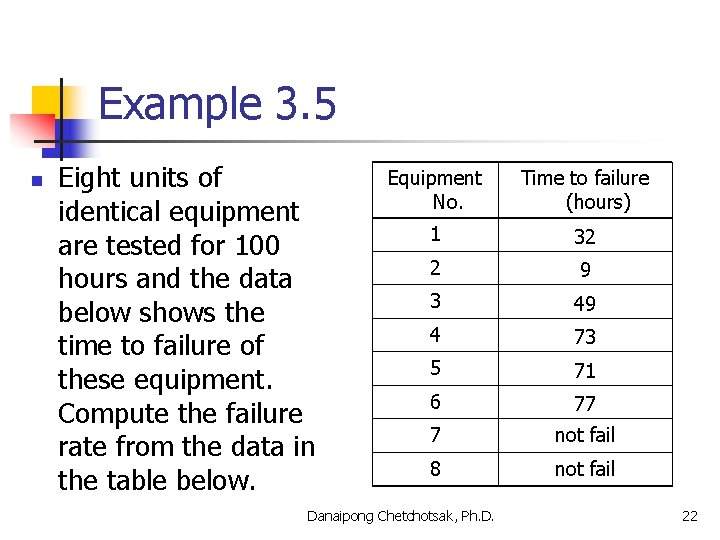
Example 3. 5 n Eight units of identical equipment are tested for 100 hours and the data below shows the time to failure of these equipment. Compute the failure rate from the data in the table below. Equipment No. Time to failure (hours) 1 32 2 9 3 49 4 73 5 71 6 77 7 not fail 8 not fail Danaipong Chetchotsak, Ph. D. 22

Example 3. 6 n Find the hazard function from the probability density function below. Danaipong Chetchotsak, Ph. D. 23
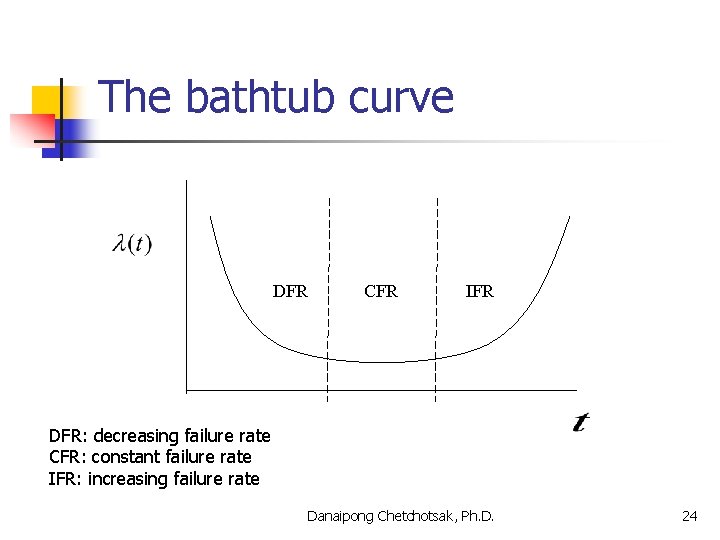
The bathtub curve DFR CFR IFR DFR: decreasing failure rate CFR: constant failure rate IFR: increasing failure rate Danaipong Chetchotsak, Ph. D. 24
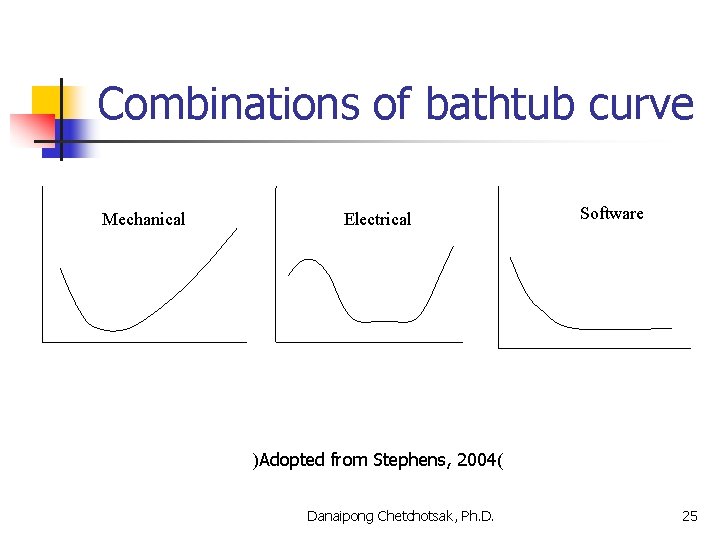
Combinations of bathtub curve Mechanical Electrical Software )Adopted from Stephens, 2004( Danaipong Chetchotsak, Ph. D. 25

Cumulative hazard function and average failure rate n n Cumulative hazard function is defined as From the eqn above, we can compute the average failure rate within the period of (t 1, t 2) as below Danaipong Chetchotsak, Ph. D. 26

Cumulative hazard function and average failure rate (cont’d) n If the average failure rate is computed over the period (0, t) Note: R(0)=1 and ln(1) =0 Danaipong Chetchotsak, Ph. D. 27

Example 3. 8 n Compute the average failure rate for a piece of equipment over the first 500 operating hours. The failure distribution of the equipment is as below: Danaipong Chetchotsak, Ph. D. 28

Conditional Reliability n Recall that the conditional probability is written as Danaipong Chetchotsak, Ph. D. 29

Conditional Reliability (cont’d) n Let A be the event that there is no failure during (t 0, t 0+t) and let B be the event that there is no failure during (0, t 0) as shown below A B 0 t 0+t Danaipong Chetchotsak, Ph. D. 30

Conditional Reliability (cont’d) t 0 is the burn-in period Danaipong Chetchotsak, Ph. D. 31

Example 3. 9 n Suppose that the reliability function for a piece of equipment is as below where t is in years. Will a burn-in period of 6 months help to improve the reliability? Danaipong Chetchotsak, Ph. D. 32

Example solution n Without a burn-in process n Suppose that the equipment is to be used for 10 years without a burn-in process. Thus t=10 and Danaipong Chetchotsak, Ph. D. 33

Example solution n With a burn-in process n Suppose the equipment has been burnt-in for 6 months and is to be used for 10 years. Thus t 0=0. 5 and the reliability will be Danaipong Chetchotsak, Ph. D. 34
- Slides: 34