Chapter 11 Discrete Optimization Models q Opt Theory

Chapter 11. Discrete Optimization Models q Opt Theory 2019 1

q Opt Theory 2019 2

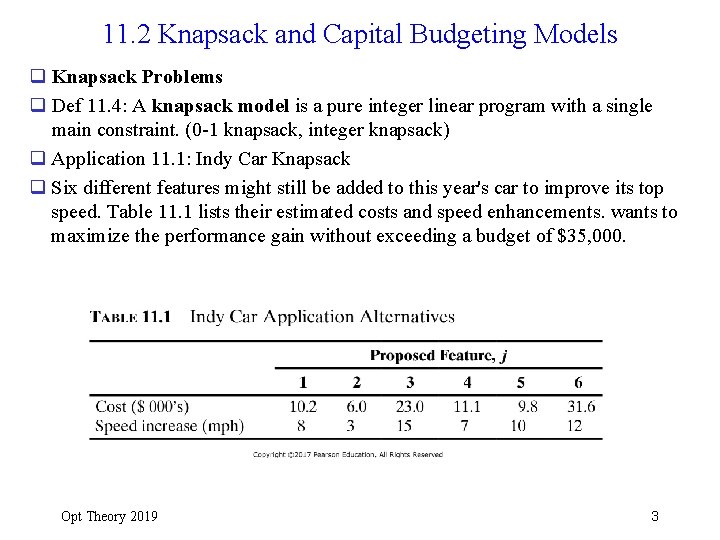
11. 2 Knapsack and Capital Budgeting Models q Knapsack Problems q Def 11. 4: A knapsack model is a pure integer linear program with a single main constraint. (0 -1 knapsack, integer knapsack) q Application 11. 1: Indy Car Knapsack q Six different features might still be added to this year's car to improve its top speed. Table 11. 1 lists their estimated costs and speed enhancements. wants to maximize the performance gain without exceeding a budget of $35, 000. Opt Theory 2019 3

q Opt Theory 2019 4

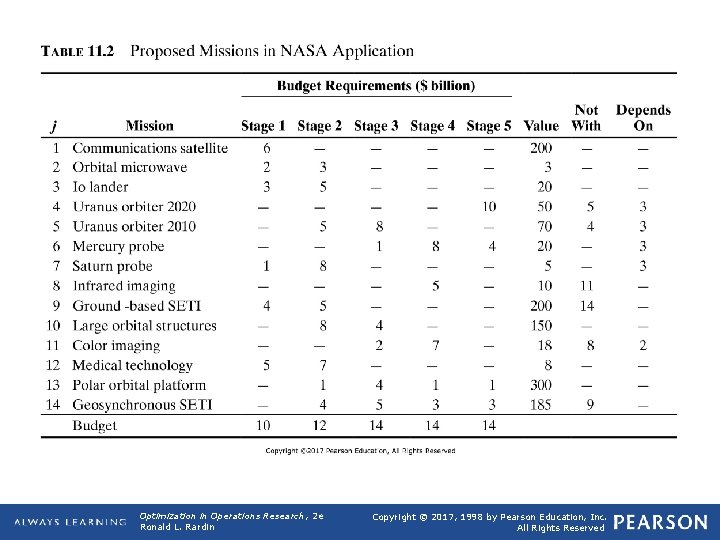
q Capital Budgeting Models q Def 11. 5: Capital budgeting models (or multidimensional knapsacks) select a maximum value collection of project, investment, and so on, subject to limitations on budgets or other resources consumed. q Application 11. 2: NASA Capital Budgeting Ø Based on G. W. Evans and R. Fairbairn (1989), "Selection and Scheduling of Advanced Missions for NASA Using 0 -1 Integer Linear Programming”, Journal of the Operational Research Society, 40, 971 -981. q NASA wants to allocate limited budgets among many competing missions proposed (Table 11. 2). We must decide which of the 14 indicated missions to include in program plans over 5 stages of a 25 -year era Opt Theory 2019 5

TABLE 11. 2 Proposed Missions in NASA Application Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

q Opt Theory 2019 7

q Opt Theory 2019 8

q Opt Theory 2019 9

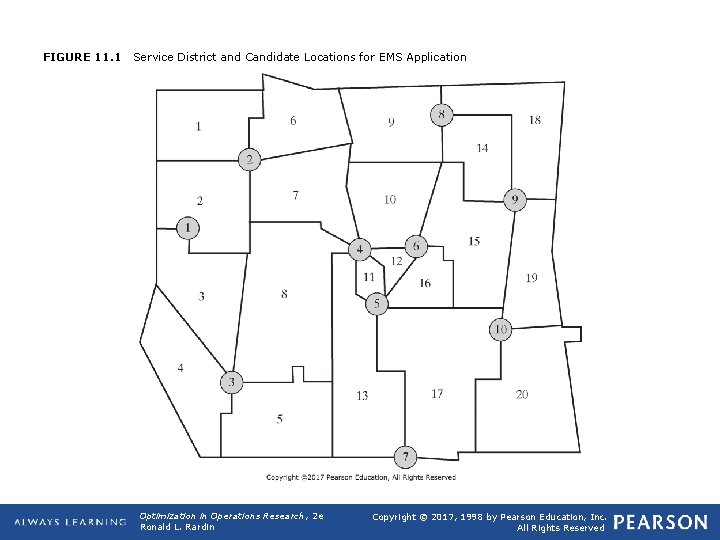
11. 3 Set Packing, Covering, and Partitioning Models q Application 11. 3: EMS Location Planning Ø Based on D. J. Eaton, M. S. Daskin, D. Simmons, Bill Bulloch, and G. Jansma (1985), “Determining Emergency Medical Service Vehicle Deployment in Austin, Texas”, Interfaces, 15: 1, 96 -108. q Austin, Texas undertook a study of the positioning of its emergency medical service (EMS) vehicles. The city was divided into service districts needing EMS services, and vehicle stations selected from a list of alternatives so that as much of the population as possible would experience a quick response to calls for help. (Figure 11. 1) Opt Theory 2019 10

FIGURE 11. 1 Service District and Candidate Locations for EMS Application Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

q Opt Theory 2019 12

q Opt Theory 2019 13

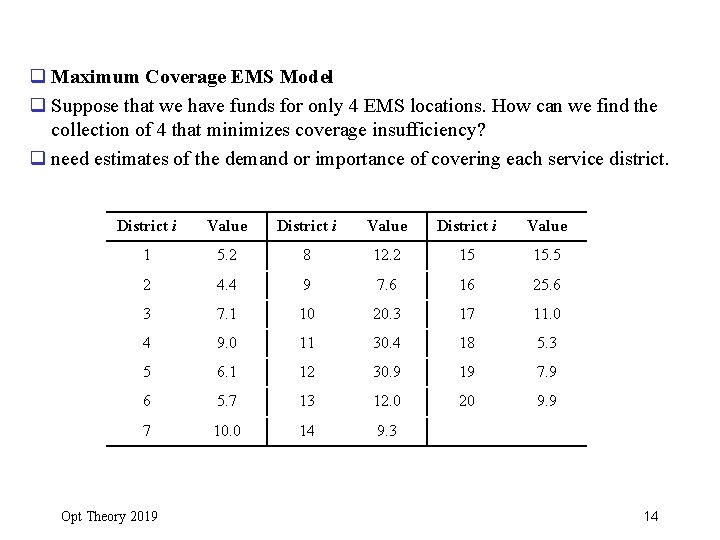
q Maximum Coverage EMS Model q Suppose that we have funds for only 4 EMS locations. How can we find the collection of 4 that minimizes coverage insufficiency? q need estimates of the demand or importance of covering each service district. District i Value 1 5. 2 8 12. 2 15 15. 5 2 4. 4 9 7. 6 16 25. 6 3 7. 1 10 20. 3 17 11. 0 4 9. 0 11 30. 4 18 5. 3 5 6. 1 12 30. 9 19 7. 9 6 5. 7 13 12. 0 20 9. 9 7 10. 0 14 9. 3 Opt Theory 2019 14

q Opt Theory 2019 15

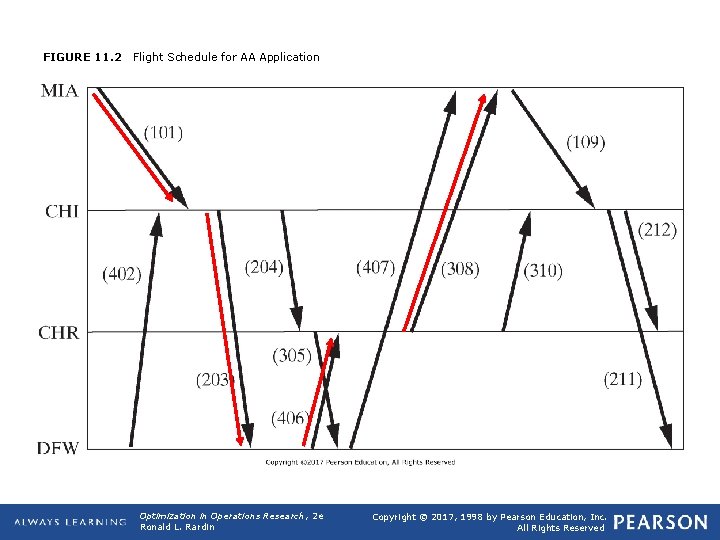
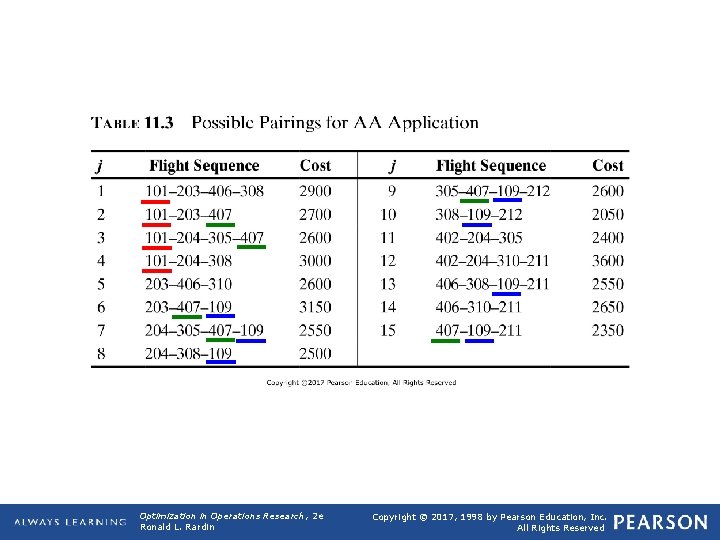
q Column Generation Models q Def 11. 13: Column generation approaches deal with complex combinatorial problems by first enumerating a sequence of columns representing viable solutions to parts of the problem, and then solving a set partitioning (or covering or packing) model to select an optimal collection of these alternatives fulfilling all problem requirements. (See also Section 13. 1). q Application 11. 4: AA Crew Scheduling Ø Based on R. Anbil, E. Gelman, B. Patty, and R. Tanga (1991), “Recent Advances in Crew-Pairing Optimization at American Airlines”, Interfaces, 21: 1, 62 -74. q Problem of scheduling crews for airlines. AA spends over $1. 3 billion per year on salaries, benefits, and travel expenses of air crews. Careful scheduling, or crew pairing as it is called, can produce enormous savings. (Figure 11. 2) q Each pairing is a sequence of flights to be covered by a single crew over a 2 - to 3 -day period. It must begin and end in the base city where the crew resides. q Table 11. 3 enumerates possible pairings of flights in Figure 11. 2. For example, pairing j = 1 begins at Miami with flight 101. After a layover in Chicago, the crew covers flight 203 to Dallas-Ft. Worth and then flight 406 to Charlotte. Finally, flight 308 returns them to Miami. Opt Theory 2019 16

FIGURE 11. 2 Flight Schedule for AA Application Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

TABLE 11. 3 Possible Pairings for AA Application Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

q Opt Theory 2019 19

q Opt Theory 2019 20

11. 4 Assignment and Matching Models q Opt Theory 2019 21

q Opt Theory 2019 22

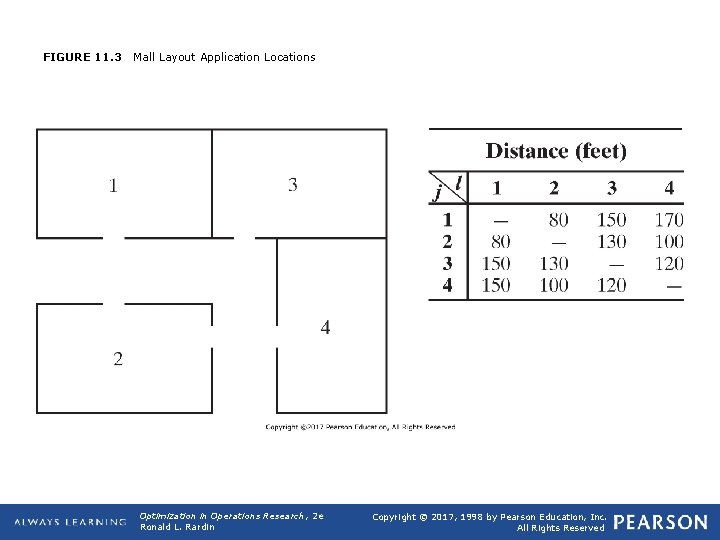
FIGURE 11. 3 Mall Layout Application Locations Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

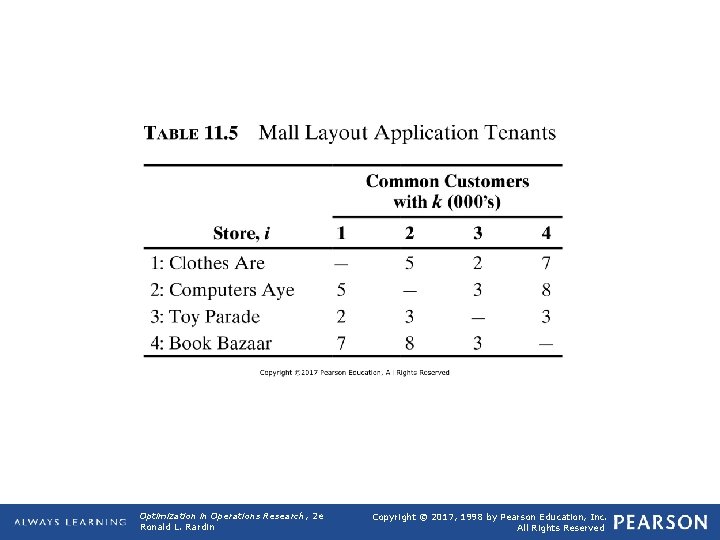
TABLE 11. 5 Mall Layout Application Tenants Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

q Opt Theory 2019 25

q Opt Theory 2019 26

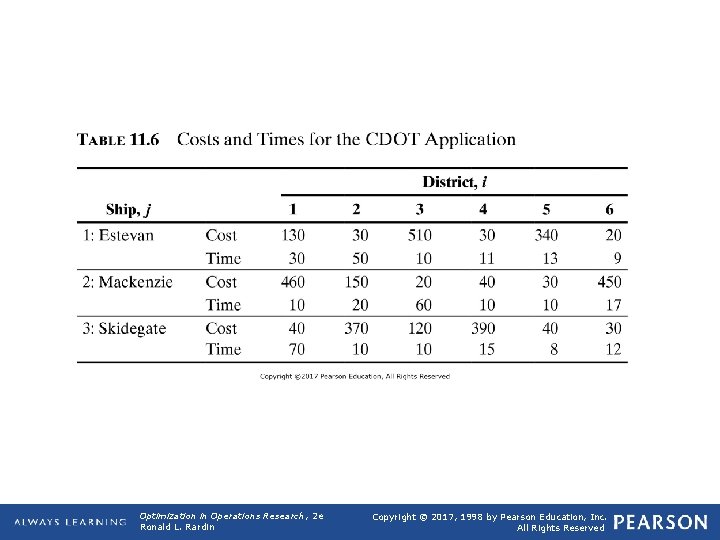
q Application 11. 6: CDOT Generalized Assignment Ø Based on J. G. Debanne and Jean-Noel Lavier (1979), "Management Science in the Public Sector-the Estevan Case, " Interfaces, 9: 2, part 2, 66 -77. q The Canadian Department of Transportation. Allocation of coast guard ships on Canada's Pacific coast. Each of the districts along the coast is assigned to one of a smaller number of coast guard ships. Since the ships have different home bases and different equipment and operating costs, the time and cost for assigning any district varies considerably among the ships. The task is to find a minimum cost assignment. Table 11. 6 shows data for our (fictitious) version of the problem. 3 ships available to serve 6 districts. Each ship is available 50 weeks per year. Opt Theory 2019 27

TABLE 11. 6 Costs and Times for the CDOT Application Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

q Opt Theory 2019 29

q Opt Theory 2019 30

q Opt Theory 2019 31

q Tractability of Assignment and Matching Models q Principle 11. 19: Linear assignment models are highly tractable because they can be viewed as network flow problems, and thus as special cases of linear programming. Even more efficient algorithms exist (Section 10. 7). q Principle 11. 20: It is very difficult to compute global optima in quadratic assignment models because the nonlinear objective function precludes even the ILP methods of Chapter 12. Improving search heuristics like those of Chapter 15 are usually applied q Principle 11. 21: Generalized assignment models, which are ILPs, can be solved in moderate size by the methods of Chapter 12. Still, they are far less tractable than the linear assignment case. q Principle 11. 22: Matching models are more difficult to solve than linear assignment cases, but efficient special-purpose algorithms are known that can solve quite large instances. Opt Theory 2019 32

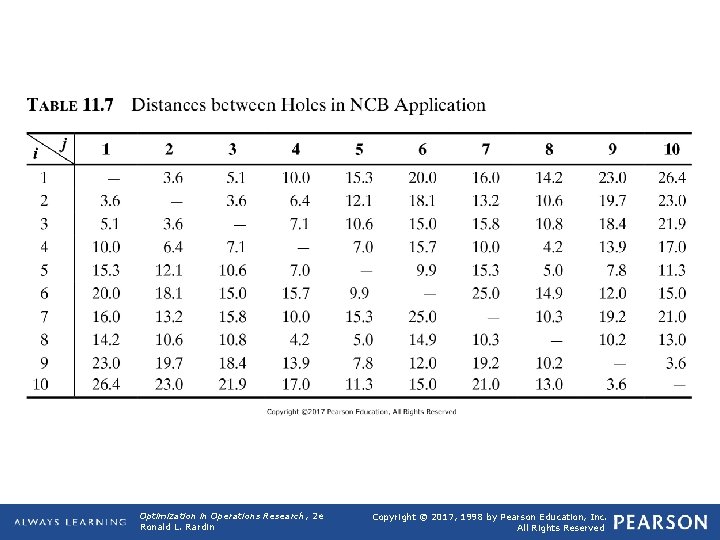
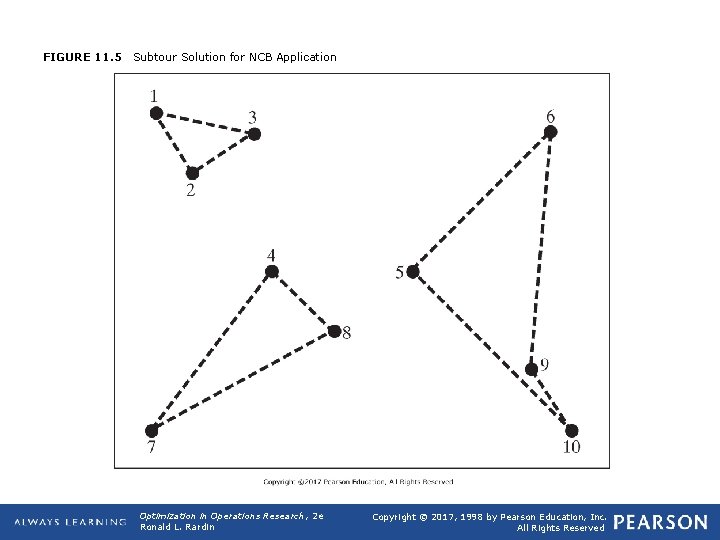
11. 5 Traveling Salesman and Routing Models q Traveling Salesman Problem q Def 11. 23: The traveling salesman problem (TSP) seeks a minimum-totallength route visiting every point in a given set exactly once. q Application 11. 8: NCB Circuit Board TSP Ø Based in part on S. Danusaputro, Chung-Yee Lee, and LA. Martin-Vega (1990), "An Efficient Algorithm for Drilling Printed Circuit Boards, " Computers and Industrial Engineering, 18, 145 -151. q Manufacture of printed circuit boards for electronics. Circuit boards have many small holes through which chips and other components are wired. Several hundred holes may have to be drilled in up to 10 different sizes. Want that these holes be completed as rapidly as possible by a moving drill. For any single size, the question of finding the most efficient drilling sequence is a traveling salesman routing problem. (similarly for SMD (surface mounting device)) q Figure 11. 4 (92. 8 inches solution, optimal is 11 inches shorter). Table 11. 7 for distance data Opt Theory 2019 33

FIGURE 11. 4 Board Drilling Locations for NCB Application Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

TABLE 11. 7 Distances between Holes in NCB Application Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

q Opt Theory 2019 36

FIGURE 11. 5 Subtour Solution for NCB Application Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

q Opt Theory 2019 38

q Opt Theory 2019 39

q Opt Theory 2019 40

q Opt Theory 2019 41

Remarks q Opt Theory 2019 42

q Opt Theory 2019 43

q Opt Theory 2019 44

q Opt Theory 2019 45

q Opt Theory 2019 46

q Opt Theory 2019 47

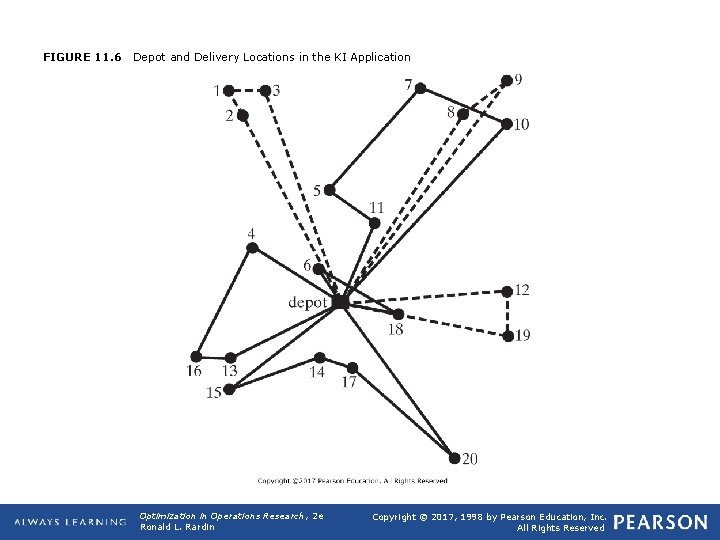
FIGURE 11. 6 Depot and Delivery Locations in the KI Application Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

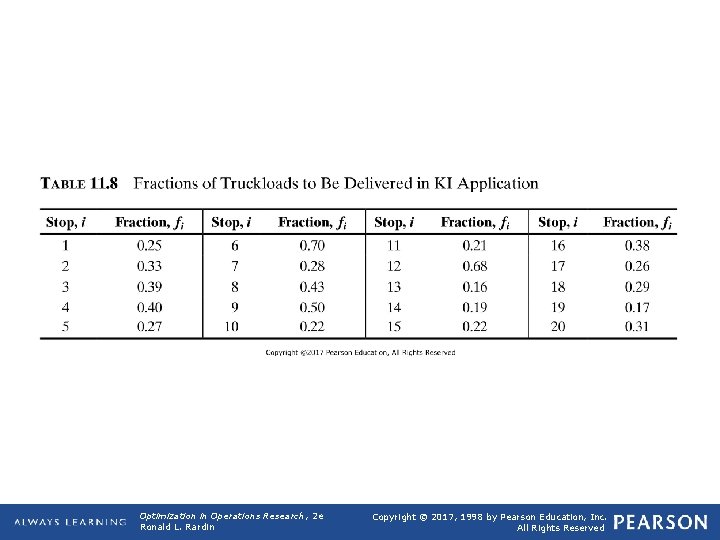
TABLE 11. 8 Fractions of Truckloads to Be Delivered in KI Application Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

q Opt Theory 2019 50

q Opt Theory 2019 51

11. 6 Facility Location and Network Design Models q Opt Theory 2019 52

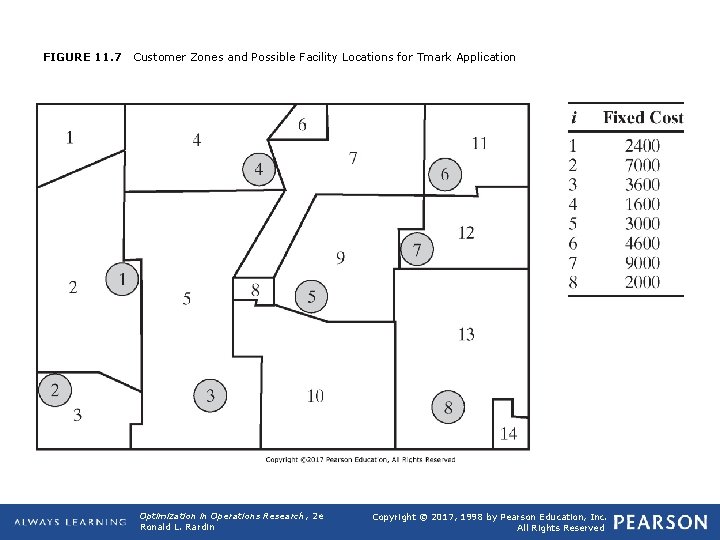
FIGURE 11. 7 Customer Zones and Possible Facility Locations for Tmark Application Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

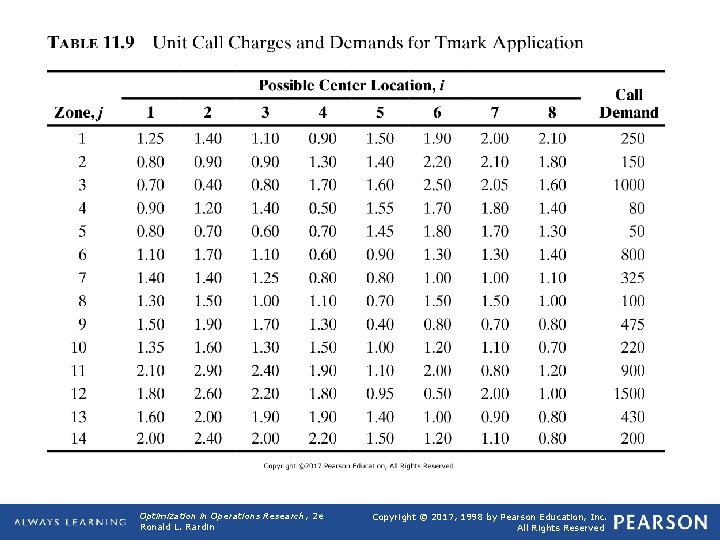
TABLE 11. 9 Unit Call Charges and Demands for Tmark Application Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

q Opt Theory 2019 55

q Opt Theory 2019 56

q Opt Theory 2019 57

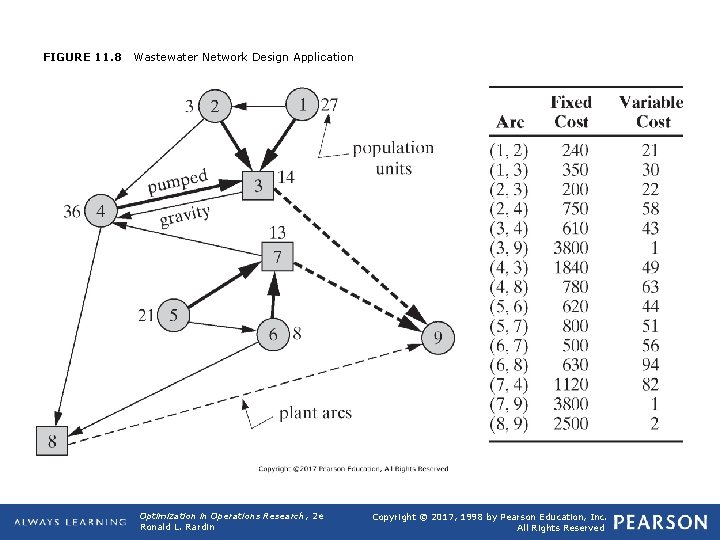
q Application 11. 11: Wastewater Network Design Ø Based on J. J. Jarvis, R. L. Rardin, V. E. Unger, R. W. Moore, and C. C. Schimpeler (1978), “Optimal Design of Regional Wastewater Systems: A Fixed Charge Network Flow Model, ” Operations Research, 26, 538– 550. q Design of regional wastewater (sewer) networks (Figure 11. 8). Nodes 1 to 8 of the network represent population centers where smaller sewers feed into the main regional network, and locations where treatment plants might be built (nodes 3, 7, and 8). q Most arcs follow the topology in gravity flow, but one pumped line (4, 3) is included. Treatment plant costs actually occur at nodes-here nodes 3, 7, and 8. Figure 11. 8 illustrates, however, that such costs can be modeled on arcs by introducing an artificial "supersink" node 9. Costs shown for arcs (3, 9), (7, 9), and (8, 9) capture the fixed and variable expense of plant construction as flows depart the network. Opt Theory 2019 58

FIGURE 11. 8 Wastewater Network Design Application Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

q Opt Theory 2019 60

11. 7 Processor Scheduling and Sequencing Models q Opt Theory 2019 61

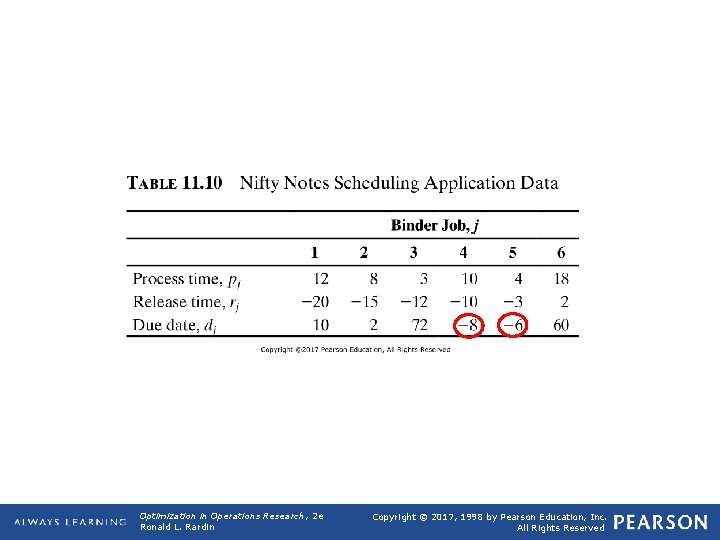
TABLE 11. 10 Nifty Notes Scheduling Application Data Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

q Opt Theory 2019 63

q Opt Theory 2019 64

q Opt Theory 2019 65

q Opt Theory 2019 66

q Opt Theory 2019 67

q Opt Theory 2019 68

q Opt Theory 2019 69

q Opt Theory 2019 70

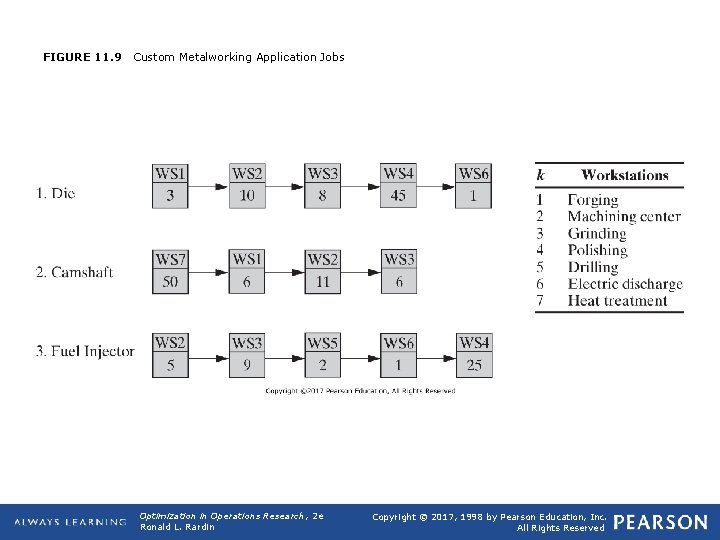
FIGURE 11. 9 Custom Metalworking Application Jobs Optimization in Operations Research, 2 e Ronald L. Rardin Copyright © 2017, 1998 by Pearson Education, Inc. All Rights Reserved

q Opt Theory 2019 72

q Opt Theory 2019 73

q See the complete model (11. 28) on page 612. Optimal value is 88 minutes. Opt Theory 2019 74