Chapter 11 Counting Methods Intro to Counting Methods

Chapter 11 – Counting Methods Intro to Counting Methods Section 11. 1: Counting by Systematic Listing

There are 3 ways to systematically list all the possible outcomes of an event: 1. Listing all Possiblities 2. Product Tables 3. Tree Diagrams

How many ways can a 6 member club elect a President? Club Members: Aaron, Bob, Carly, Debbie, Eddie and Frank Six Possible Presidents: Aaron, Bob, Carly, Debbie, Eddie, Frank

How many ways can a 6 member club elect a President and Vice President? Systematic Listing of Club Members: Aaron, Bob, Carly, Debbie, Eddie, Frank For simplicity lets let: A =Aaron, B=Bob, C =Carly, D =Debbie, E =Eddie, F =Frank

We will list the President first and the Vice President second. Choose someone to be President. A Then list all the possible Vice Presidents with your President.

We will list the President first and the Vice President second. Choose someone to be President. AB AC AD AE AF Then list all the possible Vice Presidents with your President.

Choose another President and match all the possible Vice Presents with that President. AB AC AD AE AF BA BC BD BE BF

Continue this process until you have listed all possible President-Vice President combinations. AB BA CA DA EA FA AC BC CB DB EB FB AD BD CD DC EC FC AE BE CE DE ED FD AF BF CF DF EF FE Is the combination AB the same as BA? Why or why not?

Try this one on your own… Consider two six sided cubes. The first one is numbered 1 – 6 and the second one is lettered A – F. What are all the possible outcomes of rolling these two cubes together?

1 A 1 B 1 C 1 D 1 E 1 F 2 A 2 B 2 C 2 D 2 E 2 F 3 A 3 B 3 C 3 D 3 E 3 F 4 A 4 B 4 C 4 D 4 E 4 F 5 A 5 B 5 C 5 D 5 E 5 F 6 A 6 B 6 C 6 D 6 E 6 F Why does this event have 36 possible outcomes while Example 1 only has 30 outcomes?

2. Product Tables When we have an event that involves two tasks (i. e. Choosing a President and a Vice President or rolling two cubes) we can use a product table to show all possible combinations.

Listing the presidents across the top and vice presidents along the side we have…. President Vice President A A B C D E F AB AC AD AE AF B C BA CA CB BC BD CD BE CE BF CF D E F DA EA FA DB EB FB DC EC FC ED FD FE DE DF EF

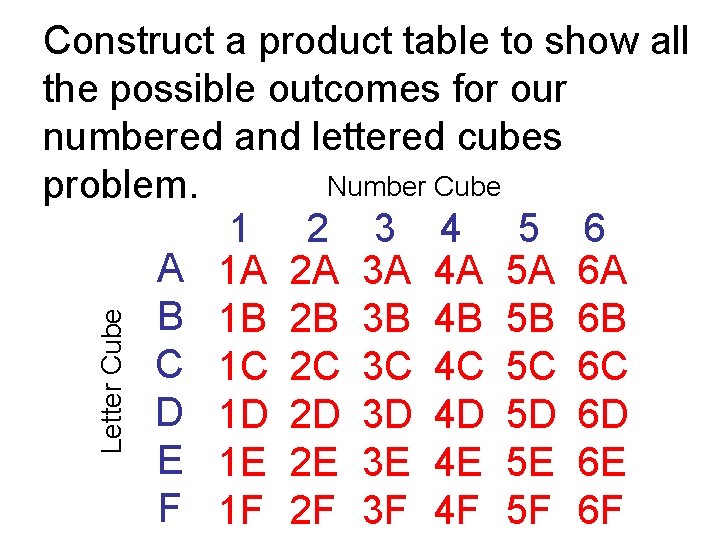
Letter Cube Construct a product table to show all the possible outcomes for our numbered and lettered cubes Number Cube problem. 1 2 3 4 5 6 A 1 A 2 A 3 A 4 A 5 A 6 A B 1 B 2 B 3 B 4 B 5 B 6 B C 1 C 2 C 3 C 4 C 5 C 6 C D 1 D 2 D 3 D 4 D 5 D 6 D E 1 E 2 E 3 E 4 E 5 E 6 E F 1 F 2 F 3 F 4 F 5 F 6 F

3. Tree Diagrams Tree diagrams are another way to systematically show all possible outcomes. Tree diagrams are useful for events containing three or more parts.

Here is a tree diagram of our President -Vice President problem. President A B C D E F Vice President B C D E F A B C D F A B C D E

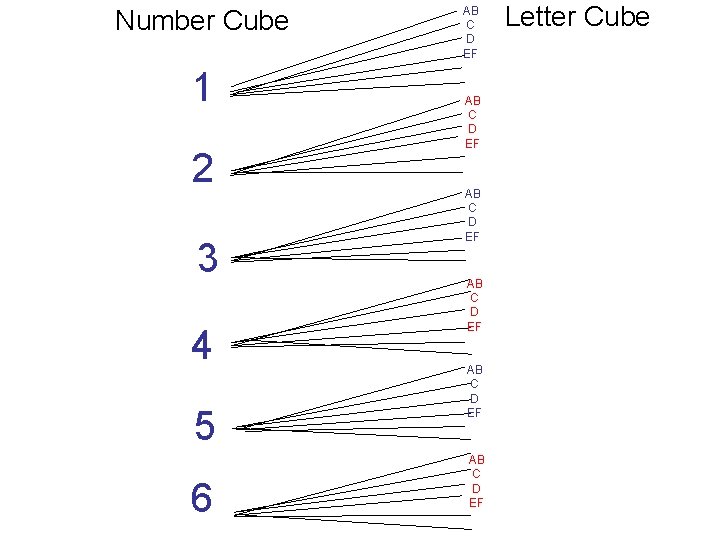
Construct a tree diagram to show all the possible outcomes for our numbered and lettered cubes problem.

Number Cube 1 2 3 4 5 6 AB C D EF AB C D EF Letter Cube

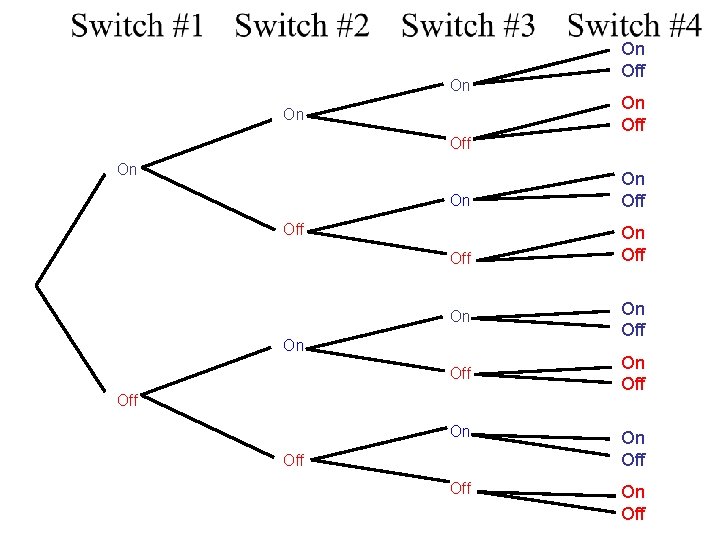
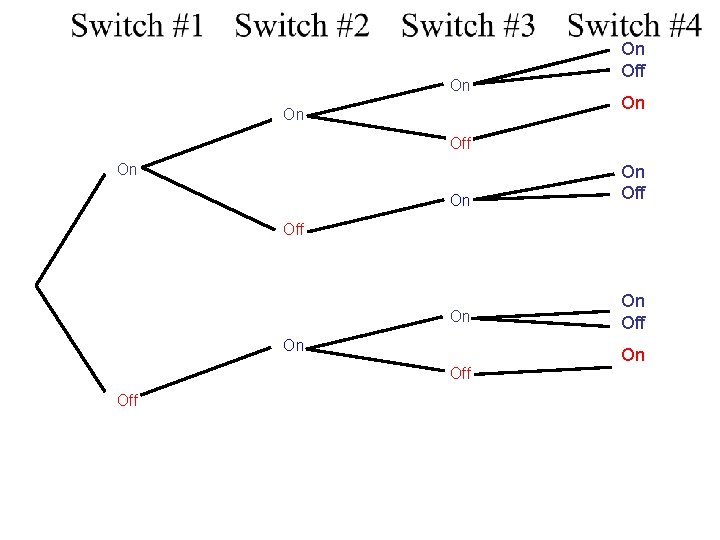
Example 7 a: Michelle’s computer printer allows for optional settings with a panel of four on-off switches. Construct a tree diagram to show all the possible ways the switches can be set.

On On Off On Off On On Off Off

Notice if we let ON be represented by 0, and OFF represented by 1

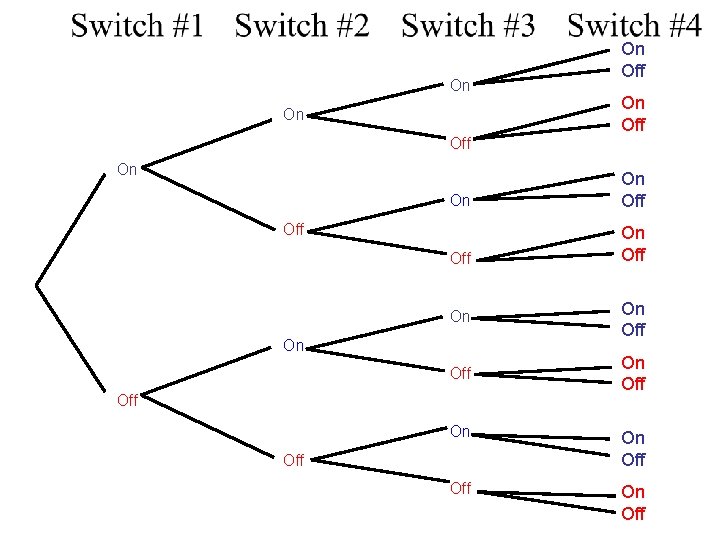
Example 7 b: Michelle’s computer printer allows for optional settings with a panel of four on-off switches. Construct a tree diagram to show all the possible ways the switches can be set if no two adjacent switches can both be off.

On On Off On Off On On Off Off

On On On Off Off On

Notice if we let ON be represented by 0, and OFF represented by 1

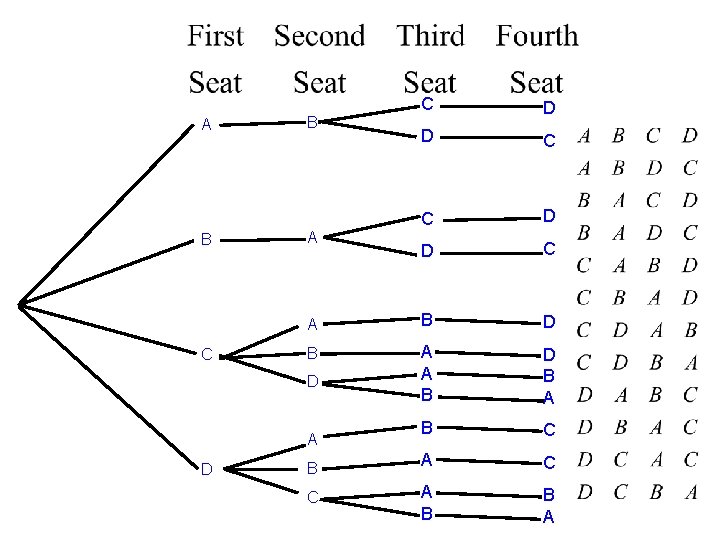
Example 8: Aaron, Bobby, Chuck and Debbie have tickets for four reserved seats in a row at a concert. What are the different ways they can seat themselves so that Aaron and Bobby will sit next to each other? Construct a tree diagram.

A B C C D D C A B D B A B C A B B A D A D B C