Chapter 11 Binary Trees Data Structures Using C

Chapter 11 Binary Trees Data Structures Using C++ 1

Chapter Objectives • • Learn about binary trees Explore various binary tree traversal algorithms Learn how to organize data in a binary search tree Discover how to insert and delete items in a binary search tree • Explore nonrecursive binary tree traversal algorithms • Learn about AVL (height-balanced) trees Data Structures Using C++ 2

Binary Trees • Definition: A binary tree, T, is either empty or such that: – T has a special node called the root node; – T has two sets of nodes, LT and RT, called the left subtree and right subtree of T, respectively; – LT and RT are binary trees Data Structures Using C++ 3

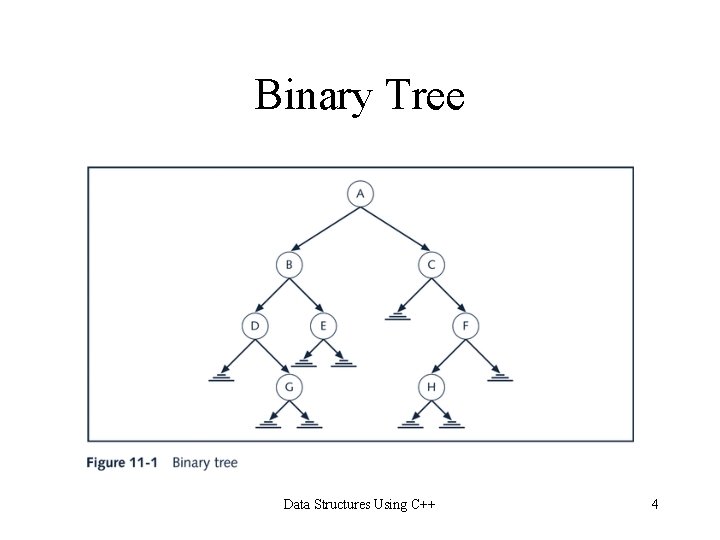
Binary Tree Data Structures Using C++ 4

Binary Tree With One Node The root node of the binary tree = A LA = empty RA = empty Data Structures Using C++ 5

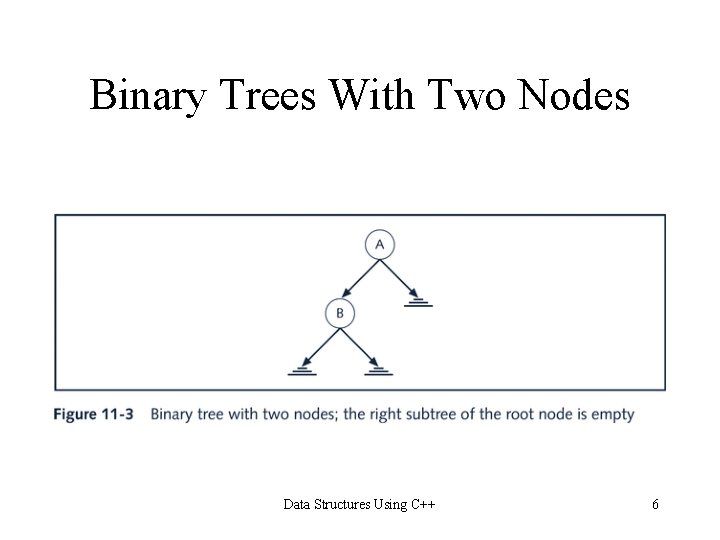
Binary Trees With Two Nodes Data Structures Using C++ 6

Binary Trees With Two Nodes Data Structures Using C++ 7

Various Binary Trees With Three Nodes Data Structures Using C++ 8

Binary Trees Following struct defines the node of a binary tree: template<class elem. Type> struct node. Type { elem. Type info; node. Type<elem. Type> *llink; node. Type<elem. Type> *rlink; }; Data Structures Using C++ 9

Nodes • For each node: – Data is stored in info – The pointer to the left child is stored in llink – The pointer to the right child is stored in rlink Data Structures Using C++ 10

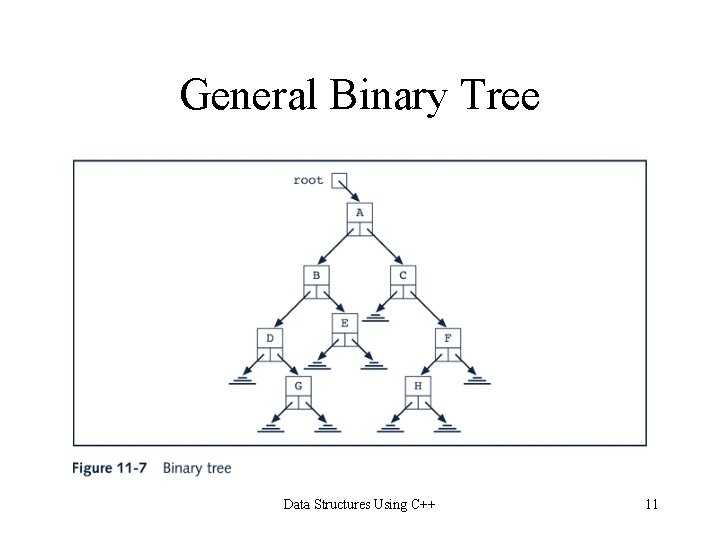
General Binary Tree Data Structures Using C++ 11

Binary Tree Definitions • Leaf: node that has no left and right children • Parent: node with at least one child node • Level of a node: number of branches on the path from root to node • Height of a binary tree: number of nodes no the longest path from root to node Data Structures Using C++ 12

Height of a Binary Tree Recursive algorithm to find height of binary tree: (height(p) denotes height of binary tree with root p): if(p is NULL) height(p) = 0 else height(p) = 1 + max(height(p->llink), height(p>rlink)) Data Structures Using C++ 13

Height of a Binary Tree Function to implement above algorithm: template<class elem. Type> int height(node. Type<elem. Type> *p) { if(p == NULL) return 0; else return 1 + max(height(p->llink), height(p->rlink)); } Data Structures Using C++ 14

Copy Tree • Useful operation on binary trees is to make identical copy of binary tree • Use function copy. Tree when we overload assignment operator and implement copy constructor Data Structures Using C++ 15

Copy Tree template<class elem. Type> void copy. Tree(node. Type<elem. Type>* &copied. Tree. Root, node. Type<elem. Type>* other. Tree. Root) { if(other. Tree. Root == NULL) copied. Tree. Root = NULL; else { copied. Tree. Root = new node. Type<elem. Type>; copied. Tree. Root->info = other. Tree. Root->info; copy. Tree(copied. Tree. Root->llink, other. Tree. Root->llink); copy. Tree(copied. Tree. Root->rlink, other. Tree. Root->rlink); } }//end copy. Tree Data Structures Using C++ 16

Binary Tree Traversal • Must start with the root, then – Visit the node first or – Visit the subtrees first • Three different traversals – Inorder – Preorder – Postorder Data Structures Using C++ 17

Traversals • Inorder – Traverse the left subtree – Visit the node – Traverse the right subtree • Preorder – Visit the node – Traverse the left subtree – Traverse the right subtree Data Structures Using C++ 18

Traversals • Postorder – Traverse the left subtree – Traverse the right subtree – Visit the node Data Structures Using C++ 19

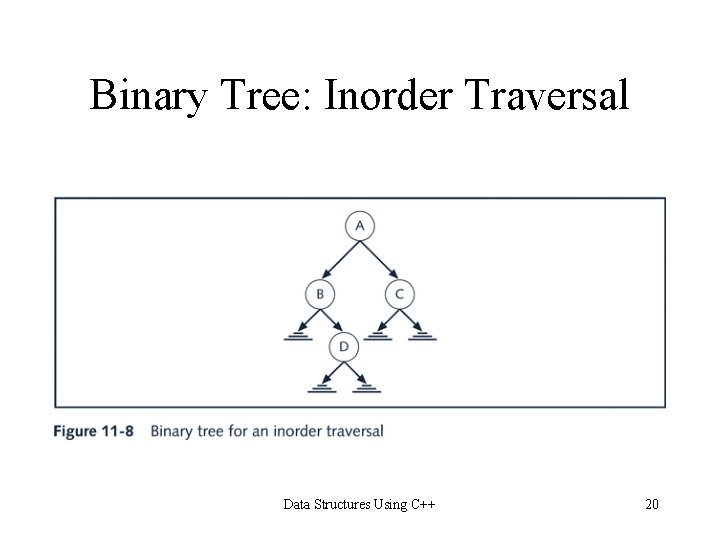
Binary Tree: Inorder Traversal Data Structures Using C++ 20

Binary Tree: Inorder Traversal template<class elem. Type> void inorder(node. Type<elem. Type> *p) { if(p != NULL) { inorder(p->llink); cout<<p->info<<” “; inorder(p->rlink); } } Data Structures Using C++ 21

Binary Tree: Traversals template<class elem. Type> void preorder(node. Type<elem. Type> *p) void postorder(node. Type<elem. Type> *p) { if(p != NULL) { { cout<<p->info<<” “; postorder(p->llink); preorder(p->llink); postorder(p->rlink); preorder(p->rlink); cout<<p->info<<” “; } }1 Data Structures Using C++ 22

Implementing Binary Trees: class binary. Tree. Type Functions • Public – – – – • Private is. Empty inorder. Traversal preorder. Traversal postorder. Traversal tree. Height tree. Node. Count tree. Leaves. Count destroy. Tree • copy. Tree • Destroy • Inorder, preorder, postorder • Height • Max • node. Count • leaves. Count Data Structures Using C++ 23

Binary Search Trees • Data in each node – Larger than the data in its left child – Smaller than the data in its right child • A binary search tree, t, is either empty or: – T has a special node called the root node – T has two sets of nodes, LT and RT, called the left subtree and right subtree of T, respectively – Key in root node larger than every key in left subtree and smaller than every key in right subtree – LT and RT are binary search trees Data Structures Using C++ 24

Binary Search Trees Data Structures Using C++ 25

Operations Performed on Binary Search Trees • Determine whether the binary search tree is empty • Search the binary search tree for a particular item • Insert an item in the binary search tree • Delete an item from the binary search tree Data Structures Using C++ 26

Operations Performed on Binary Search Trees • Find the height of the binary search tree • Find the number of nodes in the binary search tree • Find the number of leaves in the binary search tree • Traverse the binary search tree • Copy the binary search tree Data Structures Using C++ 27

Binary Search Tree Analysis Worst Case: Linear tree Data Structures Using C++ 28

Binary Search Tree Analysis • Theorem: Let T be a binary search tree with n nodes, where n > 0. The average number of nodes visited in a search of T is approximately 1. 39 log 2 n • Number of comparisons required to determine whether x is in T is one more than the number of comparisons required to insert x in T • Number of comparisons required to insert x in T same as the number of comparisons made in unsuccessful search, reflecting that x is not in T Data Structures Using C++ 29

Binary Search Tree Analysis It follows that: It is also known that: Solving Equations (11 -1) and (11 -2) Data Structures Using C++ 30

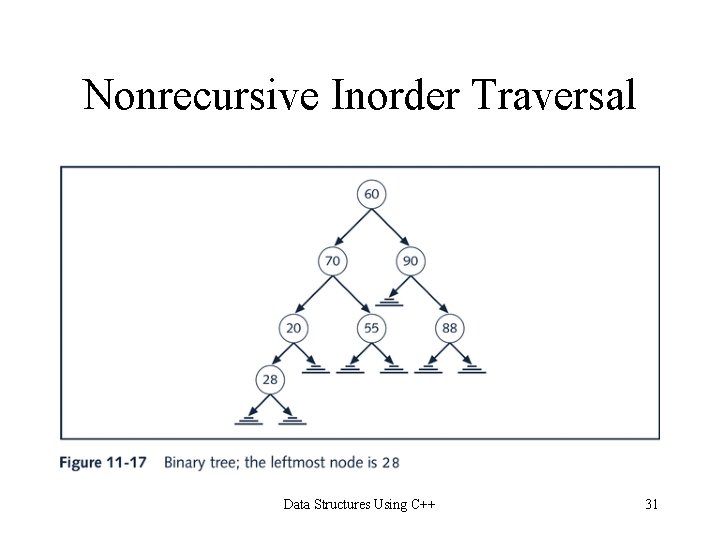
Nonrecursive Inorder Traversal Data Structures Using C++ 31

Nonrecursive Inorder Traversal: General Algorithm 1. 2. current = root; //start traversing the binary tree at // the root node while(current is not NULL or stack is nonempty) if(current is not NULL) { push current onto stack; current = current->llink; } else { pop stack into current; visit current; //visit the node current = current->rlink; //move to the //right child } Data Structures Using C++ 32

Nonrecursive Preorder Traversal: General Algorithm 1. current = root; //start the traversal at the root node 2. while(current is not NULL or stack is nonempty) if(current is not NULL) { visit current; push current onto stack; current = current->llink; } else { pop stack into current; current = current->rlink; //prepare to visit //the right subtree } Data Structures Using C++ 33

Nonrecursive Postorder Traversal 1. 2. 3. 4. current = root; //start traversal at root node v = 0; if(current is NULL) the binary tree is empty if(current is not NULL) a. push current into stack; b. push 1 onto stack; c. current = current->llink; d. while(stack is not empty) if(current is not NULL and v is 0) { push current and 1 onto stack; current = current->llink; } Data Structures Using C++ 34

Nonrecursive Postorder Traversal (Continued) else { pop stack into current and v; if(v == 1) { push current and 2 onto stack; current = current->rlink; v = 0; } else visit current; } Data Structures Using C++ 35

AVL (Height-balanced Trees) • A perfectly balanced binary tree is a binary tree such that: – The height of the left and right subtrees of the root are equal – The left and right subtrees of the root are perfectly balanced binary trees Data Structures Using C++ 36

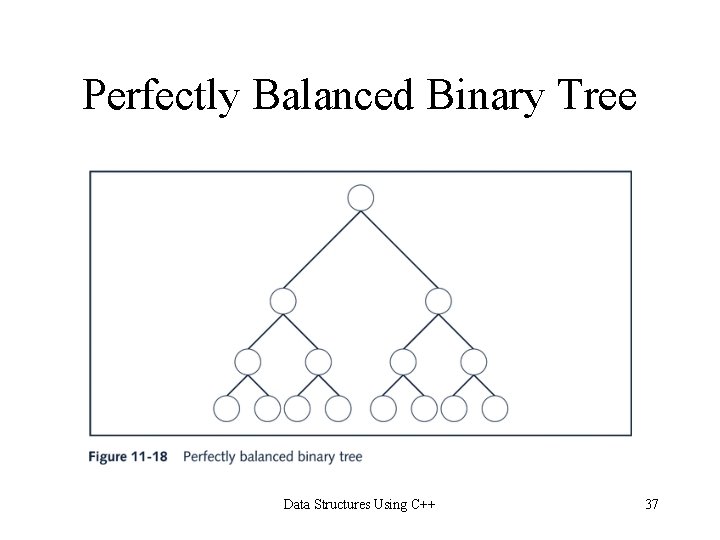
Perfectly Balanced Binary Tree Data Structures Using C++ 37

AVL (Height-balanced Trees) • An AVL tree (or height-balanced tree) is a binary search tree such that: – The height of the left and right subtrees of the root differ by at most 1 – The left and right subtrees of the root are AVL trees Data Structures Using C++ 38

AVL Trees Data Structures Using C++ 39

Non-AVL Trees Data Structures Using C++ 40

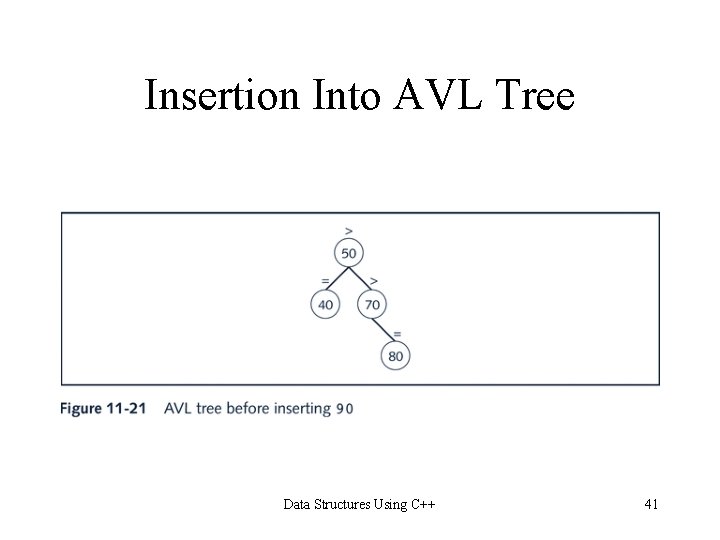
Insertion Into AVL Tree Data Structures Using C++ 41

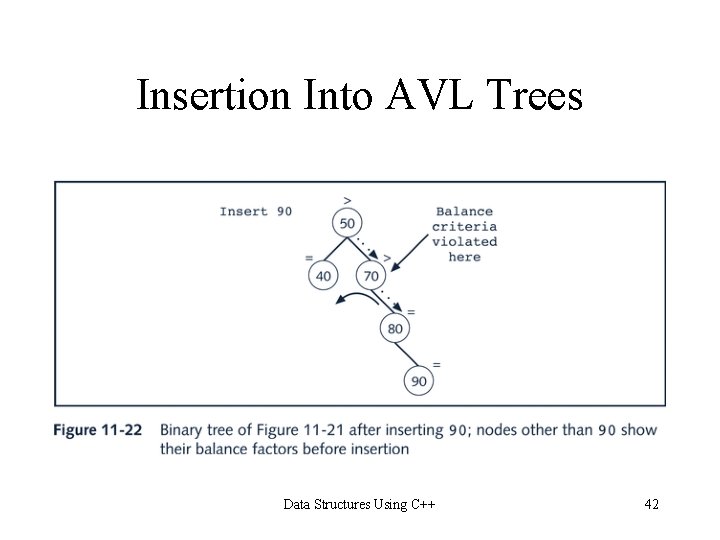
Insertion Into AVL Trees Data Structures Using C++ 42

Insertion Into AVL Trees Data Structures Using C++ 43

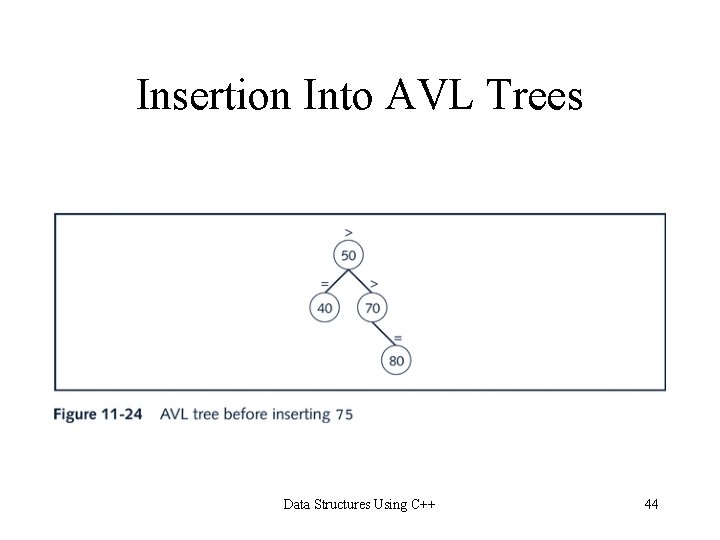
Insertion Into AVL Trees Data Structures Using C++ 44

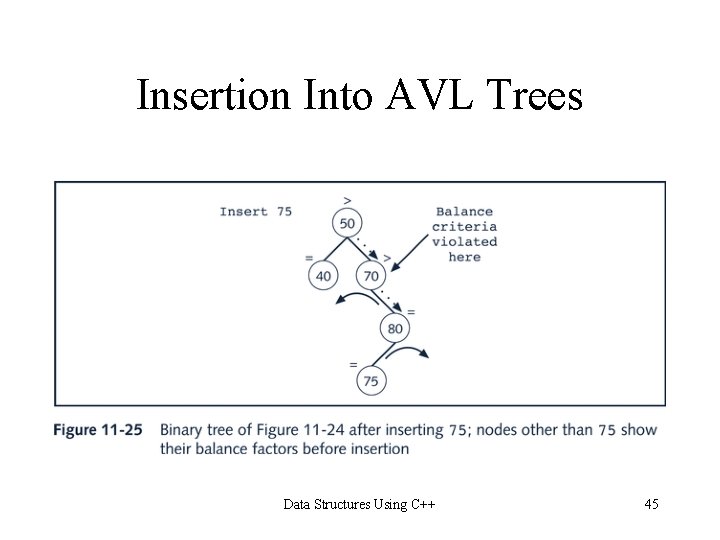
Insertion Into AVL Trees Data Structures Using C++ 45

AVL Tree Rotations • Reconstruction procedure: rotating tree • left rotation and right rotation • Suppose that the rotation occurs at node x • Left rotation: certain nodes from the right subtree of x move to its left subtree; the root of the right subtree of x becomes the new root of the reconstructed subtree • Right rotation at x: certain nodes from the left subtree of x move to its right subtree; the root of the left subtree of x becomes the new root of the reconstructed subtree Data Structures Using C++ 46

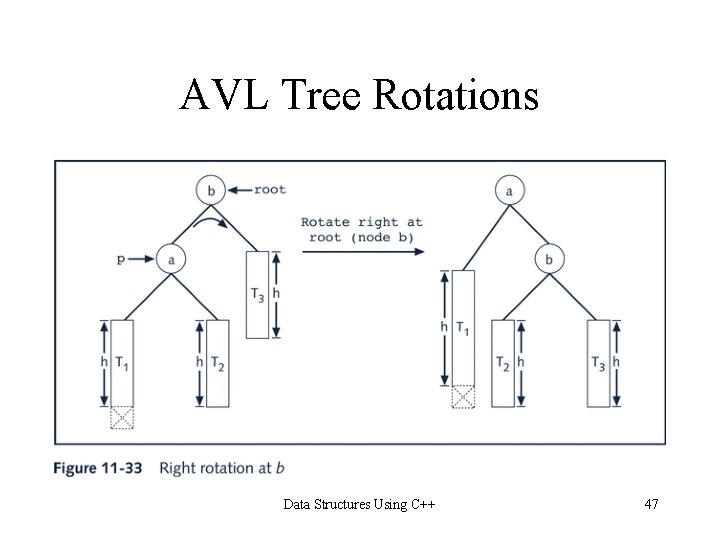
AVL Tree Rotations Data Structures Using C++ 47

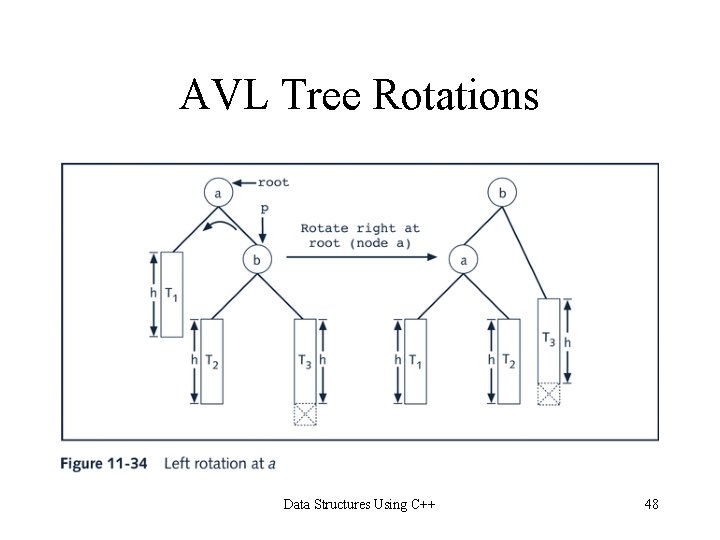
AVL Tree Rotations Data Structures Using C++ 48

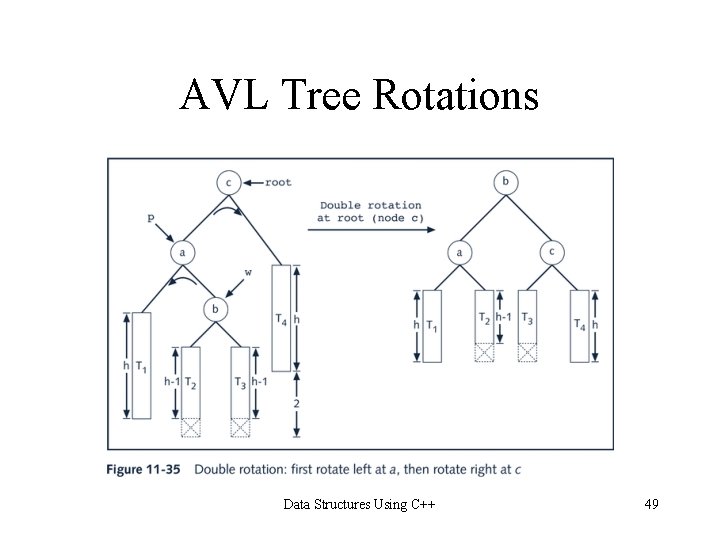
AVL Tree Rotations Data Structures Using C++ 49

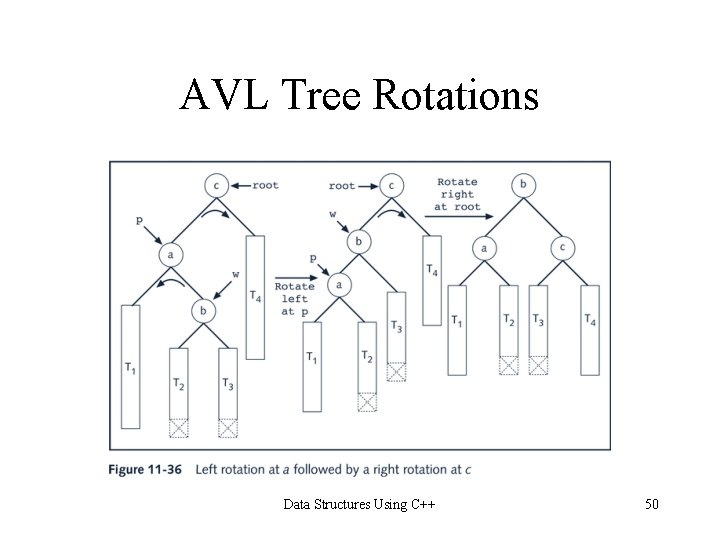
AVL Tree Rotations Data Structures Using C++ 50

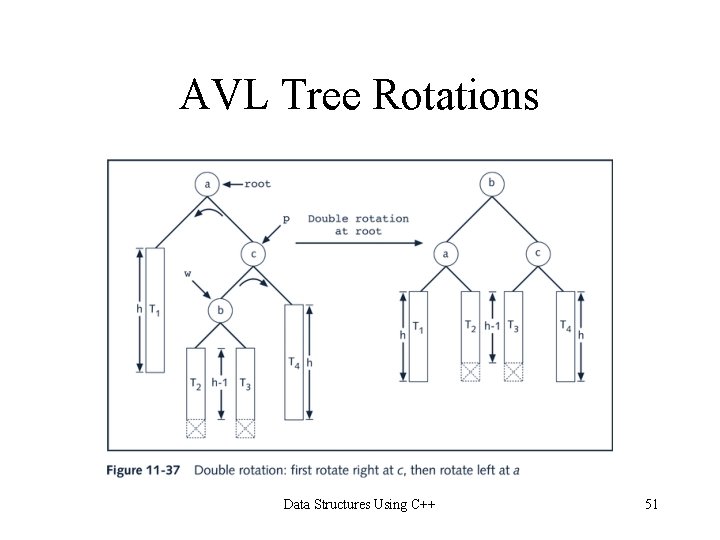
AVL Tree Rotations Data Structures Using C++ 51

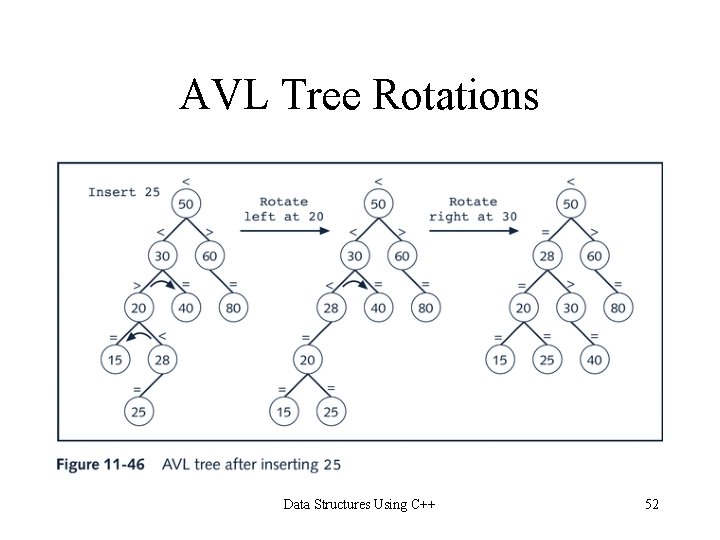
AVL Tree Rotations Data Structures Using C++ 52

Deletion From AVL Trees • Case 1: the node to be deleted is a leaf • Case 2: the node to be deleted has no right child, that is, its right subtree is empty • Case 3: the node to be deleted has no left child, that is, its left subtree is empty • Case 4: the node to be deleted has a left child and a right child Data Structures Using C++ 53

Analysis: AVL Trees Consider all the possible AVL trees of height h. Let Th be an AVL tree of height h such that Th has the fewest number of nodes. Let Thl denote the left subtree of Th and Thr denote the right subtree of Th. Then: where | Th | denotes the number of nodes in Th. Data Structures Using C++ 54

Analysis: AVL Trees Suppose that Thl is of height h – 1 and Thr is of height h – 2. Thl is an AVL tree of height h – 1 such that Thl has the fewest number of nodes among all AVL trees of height h – 1. Thr is an AVL tree of height h – 2 that has the fewest number of nodes among all AVL trees of height h – 2. Thl is of the form Th -1 and Thr is of the form Th -2. Hence: Data Structures Using C++ 55

Analysis: AVL Trees Let Fh+2 = |Th | + 1. Then: Called a Fibonacci sequence; solution to Fh is given by: Hence From this it can be concluded that Data Structures Using C++ 56

Chapter Summary • • • Binary trees Binary search trees Recursive traversal algorithms Nonrecursive traversal algorithms AVL trees Data Structures Using C++ 57