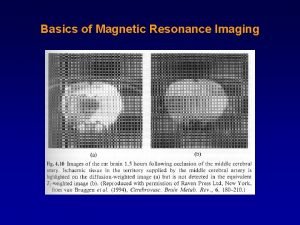
Chapter 11 Angular Momentum The Vector Product n

Chapter 11 Angular Momentum

The Vector Product n There are instances where the product of two vectors is another vector n Earlier we saw where the product of two vectors was a scalar n n This was called the dot product The vector product of two vectors is also called the cross product

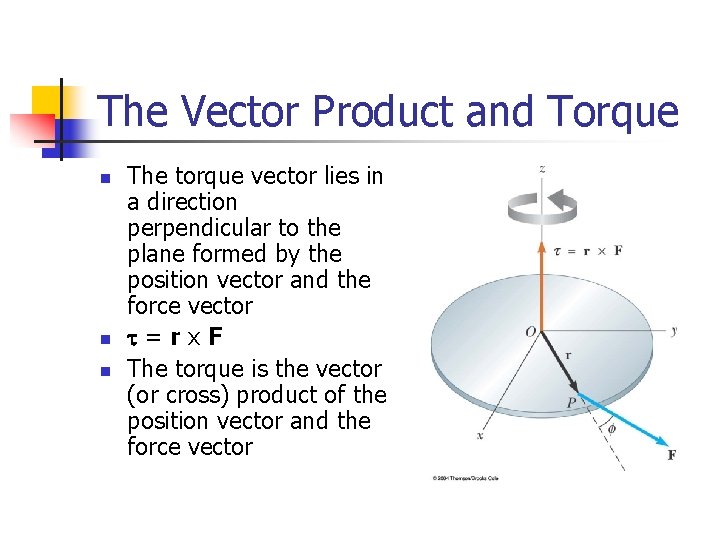
The Vector Product and Torque n n n The torque vector lies in a direction perpendicular to the plane formed by the position vector and the force vector t=rx. F The torque is the vector (or cross) product of the position vector and the force vector

The Vector Product Defined n n Given two vectors, A and B The vector (cross) product of A and B is defined as a third vector, C C is read as “A cross B” The magnitude of C is AB sin q is the angle between A and B

More About the Vector Product n n n The quantity AB sin q is equal to the area of the parallelogram formed by A and B The direction of C is perpendicular to the plane formed by A and B The best way to determine this direction is to use the right-hand rule

Properties of the Vector Product n n n The vector product is not commutative. The order in which the vectors are multiplied is important To account for order, remember Ax. B=-Bx. A If A is parallel to B (q = 0 o or 180 o), then A x B = 0 n Therefore A x A = 0

More Properties of the Vector Product n n If A is perpendicular to B, then |A x B| = AB The vector product obeys the distributive law n A x (B + C) = A x B + A x C

Final Properties of the Vector Product n The derivative of the cross product with respect to some variable such as t is where it is important to preserve the multiplicative order of A and B

Vector Products of Unit Vectors

Vector Products of Unit Vectors, cont n Signs are interchangeable in cross products n n A x (-B) = - A x B

Using Determinants n The cross product can be expressed as n Expanding the determinants gives

Torque Vector Example n Given the force n t=?

Angular Momentum n Consider a particle of mass m located at the vector position r and moving with linear momentum p

Angular Momentum, cont n The instantaneous angular momentum L of a particle relative to the origin O is defined as the cross product of the particle’s instantaneous position vector r and its instantaneous linear momentum p n L=rxp

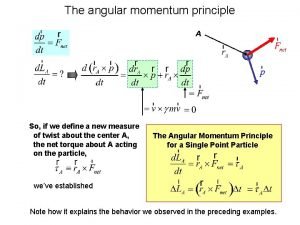
Torque and Angular Momentum n The torque is related to the angular momentum n n Similar to the way force is related to linear momentum This is the rotational analog of Newton’s Second Law n n St and L must be measured about the same origin This is valid for any origin fixed in an inertial frame

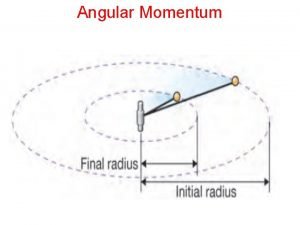
More About Angular Momentum n n n The SI units of angular momentum are (kg. m 2)/ s Both the magnitude and direction of L depend on the choice of origin The magnitude of L = mvr sin f n n f is the angle between p and r The direction of L is perpendicular to the plane formed by r and p

Angular Momentum of a Particle, Example n n The vector L = r x p is pointed out of the diagram The magnitude is L = mvr sin 90 o = mvr n n sin 90 o is used since v is perpendicular to r A particle in uniform circular motion has a constant angular momentum about an axis through the center of its path

Angular Momentum of a System of Particles n The total angular momentum of a system of particles is defined as the vector sum of the angular momenta of the individual particles n n Ltot = L 1 + L 2 + …+ Ln = SLi Differentiating with respect to time

Angular Momentum of a System of Particles, cont n n Any torques associated with the internal forces acting in a system of particles are zero Therefore, n The net external torque acting on a system about some axis passing through an origin in an inertial frame equals the time rate of change of the total angular momentum of the system about that origin

Angular Momentum of a System of Particles, final n The resultant torque acting on a system about an axis through the center of mass equals the time rate of change of angular momentum of the system regardless of the motion of the center of mass n This applies even if the center of mass is accelerating, provided t and L are evaluated relative to the center of mass

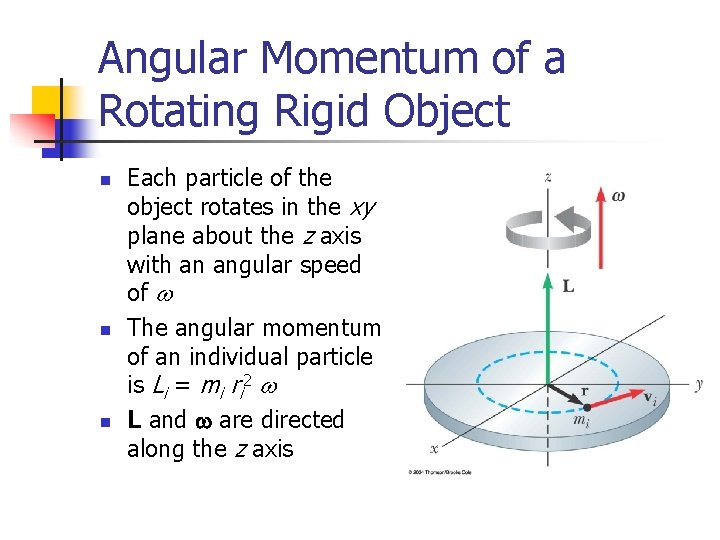
Angular Momentum of a Rotating Rigid Object n n n Each particle of the object rotates in the xy plane about the z axis with an angular speed of w The angular momentum of an individual particle is Li = mi ri 2 w L and w are directed along the z axis

Angular Momentum of a Rotating Rigid Object, cont n n To find the angular momentum of the entire object, add the angular momenta of all the individual particles This also gives the rotational form of Newton’s Second Law

Angular Momentum of a Rotating Rigid Object, final n The rotational form of Newton’s Second Law is also valid for a rigid object rotating about a moving axis provided the moving axis: (1) passes through the center of mass (2) is a symmetry axis n If a symmetrical object rotates about a fixed axis passing through its center of mass, the vector form holds: L = Iw n where L is the total angular momentum measured with respect to the axis of rotation

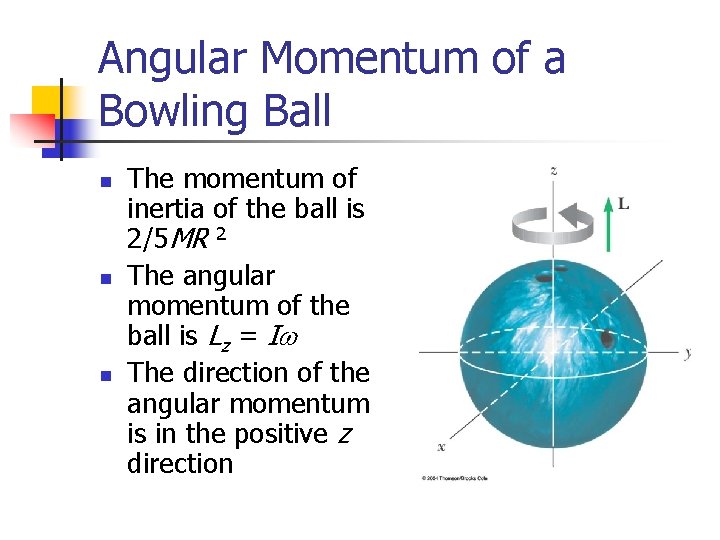
Angular Momentum of a Bowling Ball n n n The momentum of inertia of the ball is 2/5 MR 2 The angular momentum of the ball is Lz = Iw The direction of the angular momentum is in the positive z direction

Conservation of Angular Momentum n The total angular momentum of a system is constant in both magnitude and direction if the resultant external torque acting on the system is zero n n n Net torque = 0 -> means that the system is isolated Ltot = constant or Li = Lf For a system of particles, Ltot = SLn = constant

Conservation of Angular Momentum, cont n If the mass of an isolated system undergoes redistribution, the moment of inertia changes n n The conservation of angular momentum requires a compensating change in the angular velocity I i wi = I f wf n n This holds for rotation about a fixed axis and for rotation about an axis through the center of mass of a moving system The net torque must be zero in any case

Conservation Law Summary For an isolated system (1) Conservation of Energy: n n Ei = Ef (2) Conservation of Linear Momentum: n pi = pf (3) Conservation of Angular Momentum: n Li = Lf

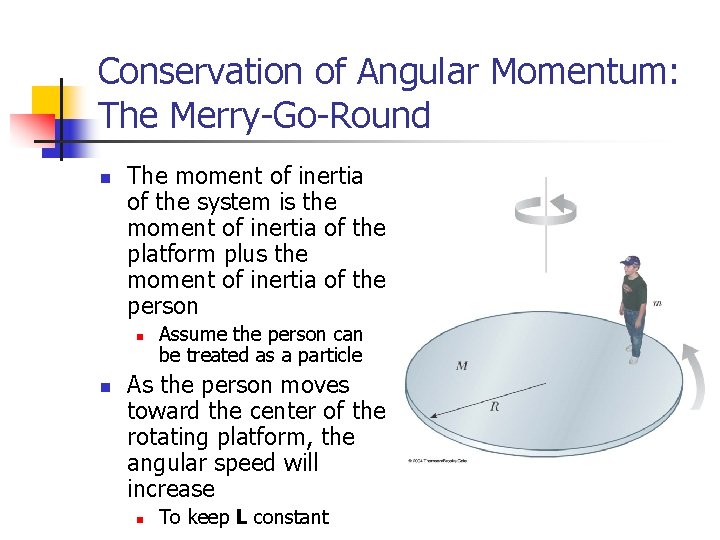
Conservation of Angular Momentum: The Merry-Go-Round n The moment of inertia of the system is the moment of inertia of the platform plus the moment of inertia of the person n n Assume the person can be treated as a particle As the person moves toward the center of the rotating platform, the angular speed will increase n To keep L constant

Motion of a Top n n n The only external forces acting on the top are the normal force n and the gravitational force M g The direction of the angular momentum L is along the axis of symmetry The right-hand rule indicates that = r F = r M g is in the xy plane

Motion of a Top, cont n The direction of d L is parallel to that of in part. The fact that Lf = d L + Li indicates that the top precesses about the z axis. n n The precessional motion is the motion of the symmetry axis about the vertical The precession is usually slow relative to the spinning motion of the top

Gyroscope n n n A gyroscope can be used to illustrate precessional motion The gravitational force Mg produces a torque about the pivot, and this torque is perpendicular to the axle The normal force produces no torque

Gyroscope, cont n n n The torque results in a change in angular momentum d L in a direction perpendicular to the axle. The axle sweeps out an angle df in a time interval dt. The direction, not the magnitude, of L is changing The gyroscope experiences precessional motion

Gyroscope, final n To simplify, assume the angular momentum due to the motion of the center of mass about the pivot is zero n n Therefore, the total angular momentum is L = Iw due to its spin This is a good approximation when w is large

Precessional Frequency n Analyzing the previous vector triangle, the rate at which the axle rotates about the vertical axis can be found n wp is the precessional frequency

Gyroscope in a Spacecraft n n The angular momentum of the spacecraft about its center of mass is zero A gyroscope is set into rotation, giving it a nonzero angular momentum The spacecraft rotates in the direction opposite to that of the gyroscope So the total momentum of the system remains zero

Angular Momentum as a Fundamental Quantity n n n The concept of angular momentum is also valid on a submicroscopic scale Angular momentum has been used in the development of modern theories of atomic, molecular and nuclear physics In these systems, the angular momentum has been found to be a fundamental quantity n n Fundamental here means that it is an intrinsic property of these objects It is a part of their nature

Fundamental Angular Momentum n n n Angular momentum has discrete values These discrete values are multiples of a fundamental unit of angular momentum The fundamental unit of angular momentum is h-bar n Where h is called Planck’s constant

Angular Momentum of a Molecule n n Consider the molecule as a rigid rotor, with the two atoms separated by a fixed distance The rotation occurs about the center of mass in the plane of the page with a speed of

Classical Ideas in Subatomic Systems n Certain classical concepts and models are useful in describing some features of atomic and molecular systems n n Proper modifications must be made A wide variety of subatomic phenomena can be explained by assuming discrete values of the angular momentum associated with a particular type of motion

Niels Bohr n n Niels Bohr was a Danish physicist He adopted the (then radical) idea of discrete angular momentum values in developing his theory of the hydrogen atom n Classical models were unsuccessful in describing many aspects of the atom

Bohr’s Hydrogen Atom n The electron could occupy only those circular orbits for which the orbital angular momentum was equal to n n n where n is an integer This means that orbital angular momentum is quantized