Chapter 11 Angular Momentum Rolling Torque and Angular

Chapter 11 Angular Momentum

Rolling, Torque, and Angular Momentum I. Rolling - Kinetic energy - Forces II. Torque III. Angular momentum - Definition IV. Newton’s second law in angular form V. Angular momentum - System of particles - Rigid body - Conservation

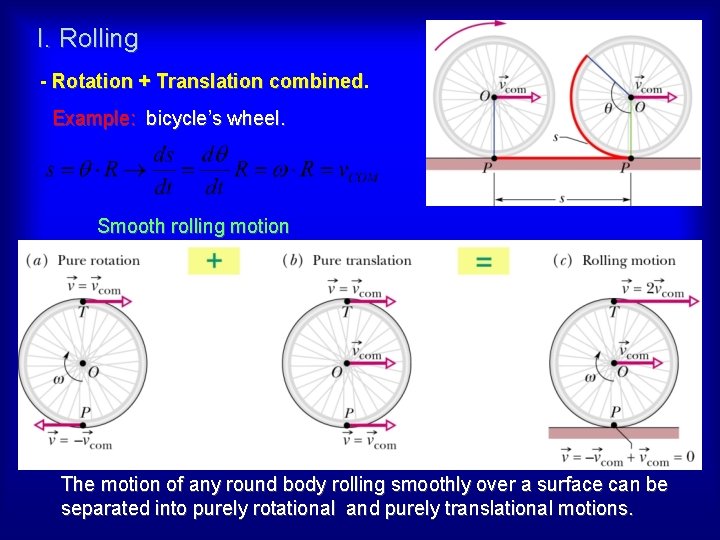
I. Rolling - Rotation + Translation combined Example: bicycle’s wheel. Smooth rolling motion The motion of any round body rolling smoothly over a surface can be separated into purely rotational and purely translational motions.

- Pure rotation. Rotation axis through point where wheel contacts ground. Angular speed about P (ω) = Angular speed (ω)about O for stationary observer. Instantaneous velocity vectors = sum of translational and rotational motions. - Kinetic energy of rolling. A rolling object has two types of kinetic energy Rotational: (about its COM). (translation of its COM). Translational:

- Forces of rolling. (a) Rolling at constant speed no sliding at P no friction. (b) Rolling with acceleration sliding at P friction force opposed to sliding. Static friction wheel does not slide smooth rolling motion a. COM = α R Sliding Increasing acceleration Example 1: wheels of a car moving forward while its tires are spinning madly, leaving behind black stripes on the road rolling with slipping = skidding Icy pavements. Anti-block braking systems are designed to ensure that tires roll without slipping during braking.

Example 2: ball rolling smoothly down a ramp. (No slipping). 1. Frictional force causes the rotation. Without friction the ball will not roll down the ramp, will just slide. Sliding tendency 2. Rolling without sliding the point of contact between the sphere and the surface is at rest the frictional force is the static frictional force. 3. Work done by frictional force = 0 the point of contact is at rest (static friction).

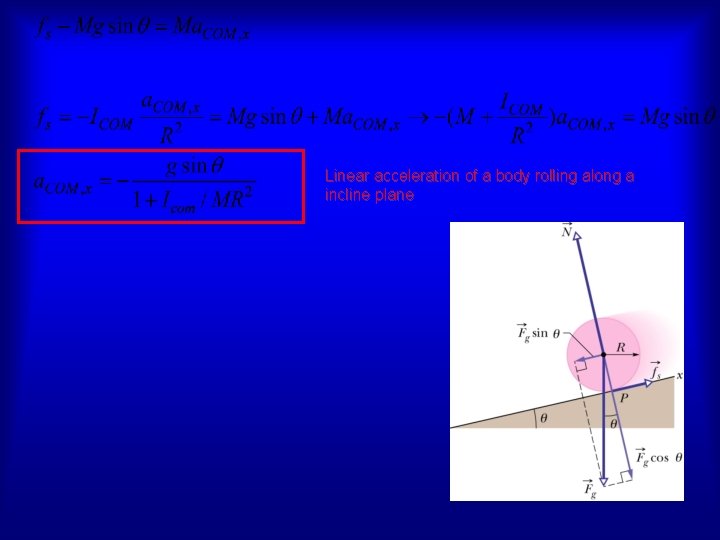
Example: ball rolling smoothly down a ramp. Note: Do not assume fs = fs, max. The only fs requirement is that its magnitude is just right for the body to roll smoothly down the ramp, without sliding. Newton’s second law in angular form Rotation about center of mass

Linear acceleration of a body rolling along a incline plane

- Yo-yo Potential energy (mgh) kinetic energy: translational (0. 5 mv 2 COM) and rotational (0. 5 ICOMω2) Analogous to body rolling down a ramp: - Yo-yo rolls down a string at an angle θ =90º with the horizontal. - Yo-yo rolls on an axle of radius R 0. - Yo-yo is slowed by the tension on it from the string.

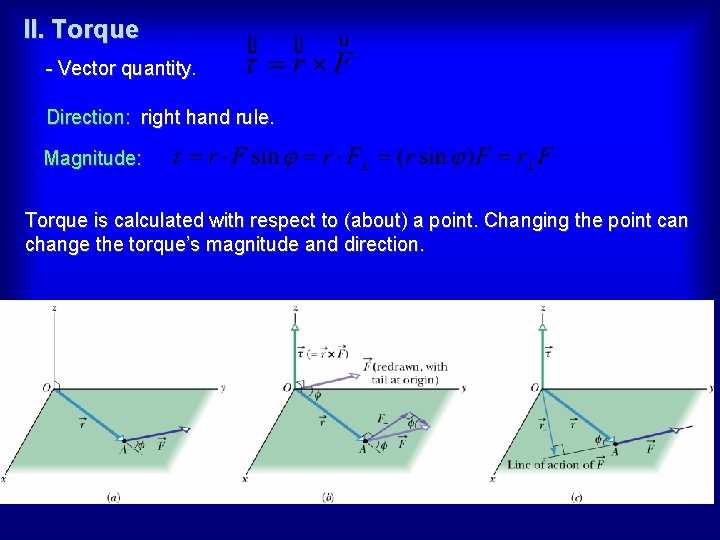
II. Torque - Vector quantity Direction: right hand rule. Magnitude: Torque is calculated with respect to (about) a point. Changing the point can change the torque’s magnitude and direction.

III. Angular momentum - Vector quantity. Units: kg m 2/s Magnitude: Direction: right hand rule. l positive counterclockwise l negative clockwise Direction of l is always perpendicular to plane formed by r and p.

IV. Newton’s second law in angular form Linear Angular Single particle The vector sum of all torques acting on a particle is equal to the time rate of change of the angular momentum of that particle. Proof: V. Angular momentum - System of particles:

Includes internal torques (due to forces between particles within system) and external torques (due to forces on the particles from bodies outside system). Forces inside system third law force pairs torqueint sum =0 The only torques that can change the angular momentum of a system are the external torques acting on a system. The net external torque acting on a system of particles is equal to the time rate of change of the system’s total angular momentum L.

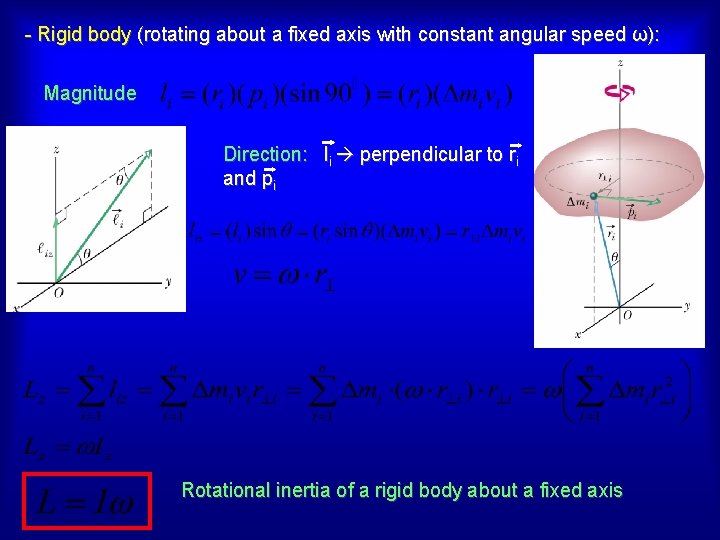
- Rigid body (rotating about a fixed axis with constant angular speed ω): Magnitude Direction: li perpendicular to ri and pi Rotational inertia of a rigid body about a fixed axis

- Conservation of angular momentum: Newton’s second law If no net external torque acts on the system (isolated system) Law of conservation of angular momentum: Net angular momentum at time ti = Net angular momentum at later time tf If the net external torque acting on a system is zero, the angular momentum of the system remains constant, no matter what changes take place within the system.

If the component of the net external torque on a system along a certain axis is zero, the component of the angular momentum of the system along that axis cannot change, no matter what changes take place within the system. This conservation law holds not only within the frame of Newton’s mechanics but also for relativistic particles (speeds close to light) and subatomic particles. ( Ii, f, ωi, f refer to rotational inertia and angular speed before and after the redistribution of mass about the rotational axis ).

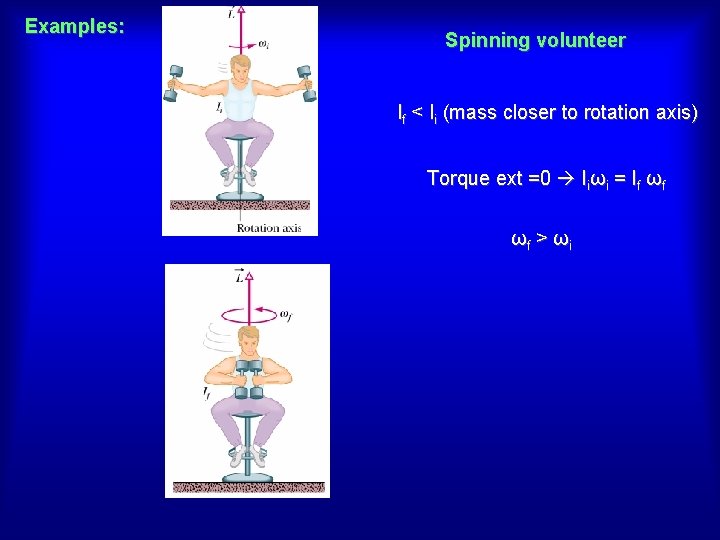
Examples: Spinning volunteer If < Ii (mass closer to rotation axis) Torque ext =0 Iiωi = If ωf ωf > ωi

A solid cylinder of radius 15 cm and mass 3. 0 kg rolls without slipping at a constant speed of 1. 6 m/s. (a) What is its angular momentum about its symmetry axis? (b) What is its rotational kinetic energy? (c) What is its total kinetic energy? ( I cylinder= ) (a) The angular speed of the cylinder is rotational inertia for cylinder , the . The angular momentum about the symmetry axis is

A solid cylinder of radius 15 cm and mass 3. 0 kg rolls without slipping at a constant speed of 1. 6 m/s. (a) What is its angular momentum about its symmetry axis? (b) What is its rotational kinetic energy? (c) What is its total kinetic energy? ( I cylinder= ) (b) (c)

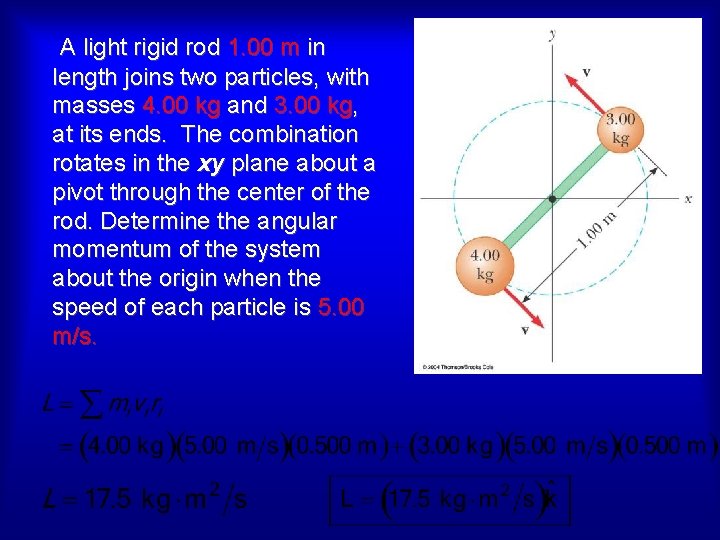
A light rigid rod 1. 00 m in length joins two particles, with masses 4. 00 kg and 3. 00 kg, at its ends. The combination rotates in the xy plane about a pivot through the center of the rod. Determine the angular momentum of the system about the origin when the speed of each particle is 5. 00 m/s.

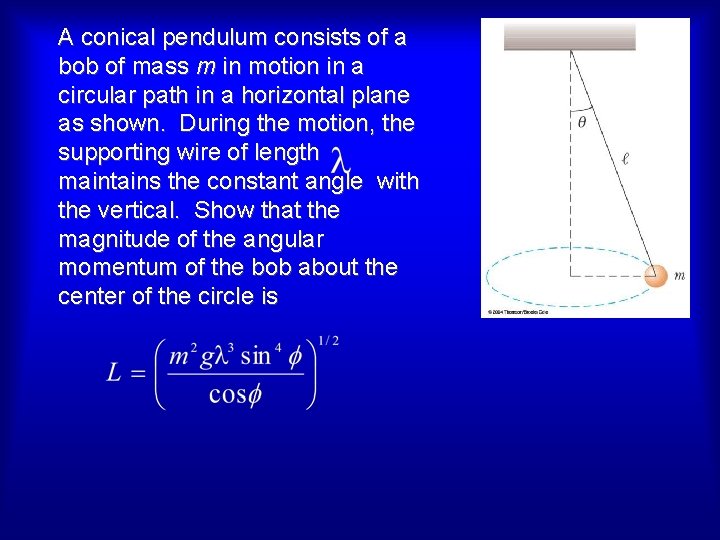
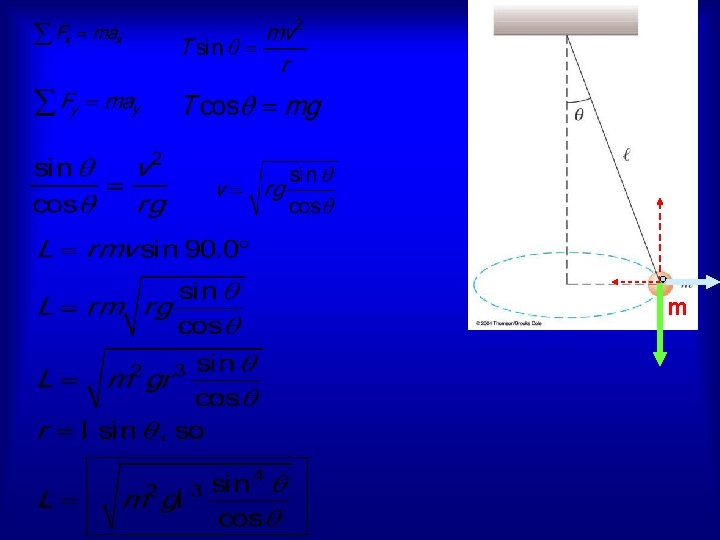
A conical pendulum consists of a bob of mass m in motion in a circular path in a horizontal plane as shown. During the motion, the supporting wire of length maintains the constant angle with the vertical. Show that the magnitude of the angular momentum of the bob about the center of the circle is

m

The position vector of a particle of mass 2. 00 kg is given as a function of time by. Determine the angular momentum of the particle about the origin, as a function of time.

A uniform solid disk is set into rotation with an angular speed i about an axis through its center. While still rotating at this speed, the disk is placed into contact with a horizontal surface and released as in the Figure. (a) What is the angular speed of the disk once pure rolling takes place? (b) Find the fractional loss in kinetic energy from the time the disk is released until pure rolling occurs. (Hint: Consider torques about the center of mass. )

(a) The net torque is zero at the point of contact, so the angular momentum before and after the collision must be equal. (b)