Chapter 10 Uniform Circular Motion Physics Centripetal forces

Chapter 10. Uniform Circular Motion Physics

Centripetal forces keep these children moving in a circular path.

Objectives: After completing this module, you should be able to: • Apply your knowledge of centripetal acceleration and centripetal force to the solution of problems in circular motion. • Define and apply concepts of frequency and period, and relate them to linear speed. • Solve problems involving banking angles, the conical pendulum, and the vertical circle.

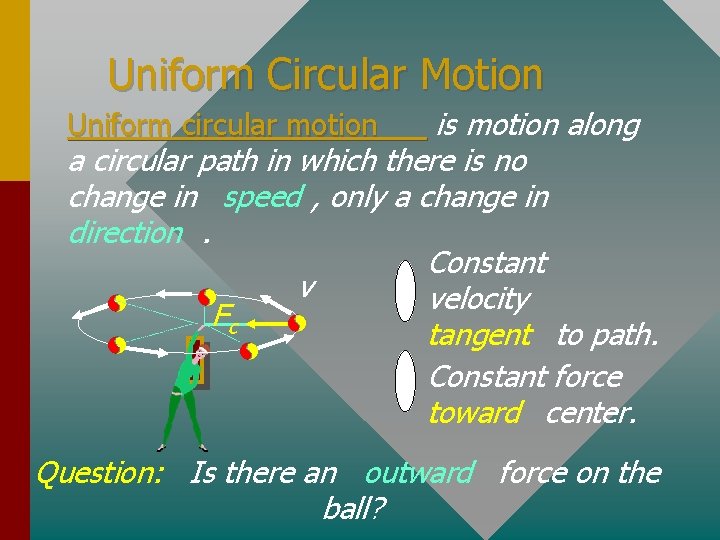
Uniform Circular Motion is motion along a circular path in which there is no change in speed , only a change in direction. Constant v velocity Fc tangent to path. Constant force toward center. Uniform circular motion Question: Is there an outward force on the ball?

Uniform Circular Motion (Cont. ) The question of an outward force can be resolved by asking what happens when the string breaks! Ball moves tangent to path, NOT v outward as might be expected. When central force is removed, ball continues in straight line. Centripetal force is needed to change direction.

Examples of Centripetal Force You are sitting on the seat next to the outside door. What is the direction of the resultant force on you as you turn? Is it away from center or toward center of the turn? • Car going around a curve. Fc Force ON you is toward the center.

Car Example Continued Reaction Fc F’ The centripetal force is exerted BY the door ON you. (Centrally) There is an outward force, but it does not act ON you. It is the reaction force exerted BY you ON the door. It affects only the door.

Another Example Disappearing platform at fair. R Fc What exerts the centripetal force in this example and on what does it act? The centripetal force is exerted BY the wall ON the man. A reaction force is exerted by the man on the wall, but that does not determine the motion of the man.

Spin Cycle on a Washer How is the water removed from clothes during the spin cycle of a washer? Think carefully before answering. . . Does the centripetal force throw water off the clothes? NO. Actually, it is the LACK of a force that allows the water to leave the clothes through holes in the circular wall of the rotating washer.

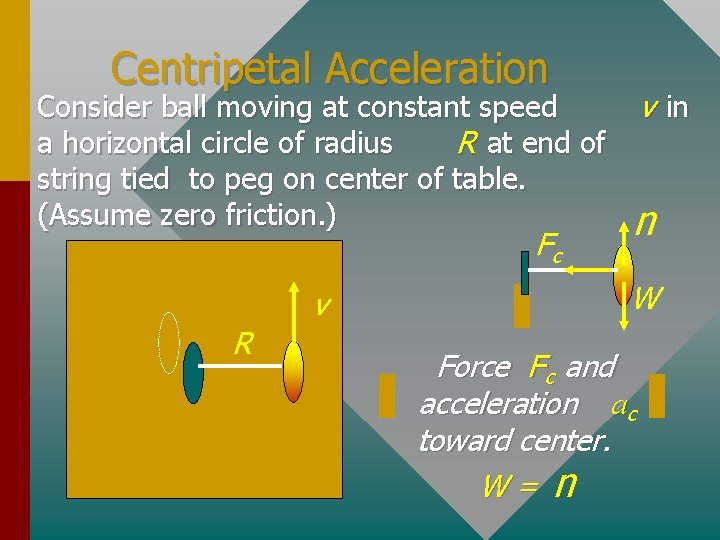
Centripetal Acceleration v in Consider ball moving at constant speed a horizontal circle of radius R at end of string tied to peg on center of table. (Assume zero friction. ) n v W Fc R Force F c and acceleration ac toward center. W= n

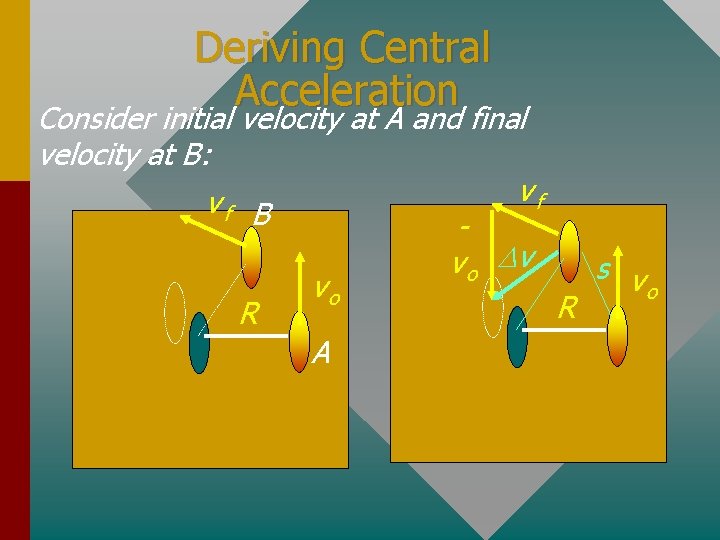
Deriving Central Acceleration Consider initial velocity at A and final velocity at B: vf vf B v o Dv s v vo o R R A

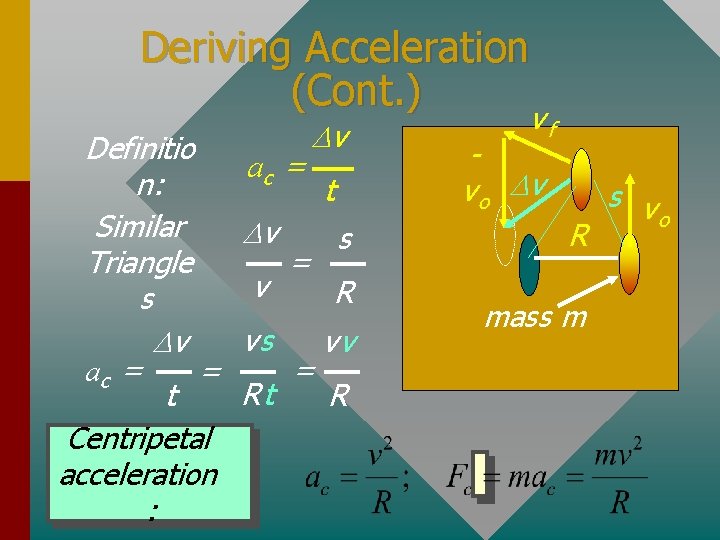
Deriving Acceleration (Cont. ) Definitio n: Similar Triangle s Dv ac = = t Centripetal acceleration : ac = Dv v vs Rt Dv = = t s R vv R vf v o Dv R mass m s v o

Example 1: A 3 -kg rock swings in a circle of radius 5 m. If its constant speed is 8 m/s , what is the centripetal acceleration? v m =3 m kg R R = 5 m ; v = 8 m/s F = (3 kg)(12. 8 m/s 2 ) F c = 38. 4 N

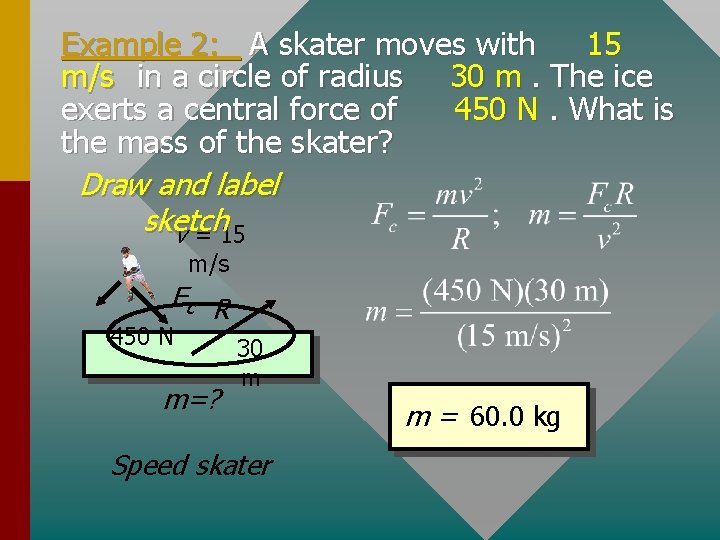
Example 2: A skater moves with 15 m/s in a circle of radius 30 m. The ice exerts a central force of 450 N. What is the mass of the skater? Draw and label sketch v = 15 m/s Fc R 450 N m=? 30 m Speed skater m = 60. 0 kg

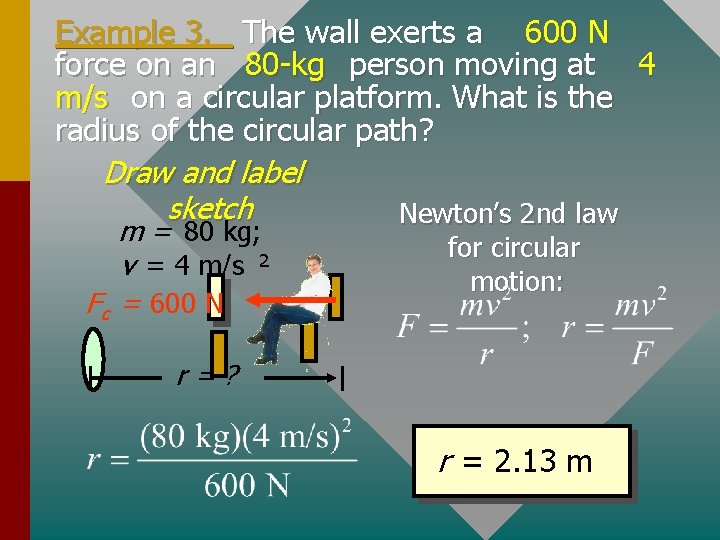
Example 3. The wall exerts a 600 N force on an 80 -kg person moving at 4 m/s on a circular platform. What is the radius of the circular path? Draw and label sketch Newton’s 2 nd law m = 80 kg; v = 4 m/s 2 F c = 600 N for circular motion: r=? r = 2. 13 m

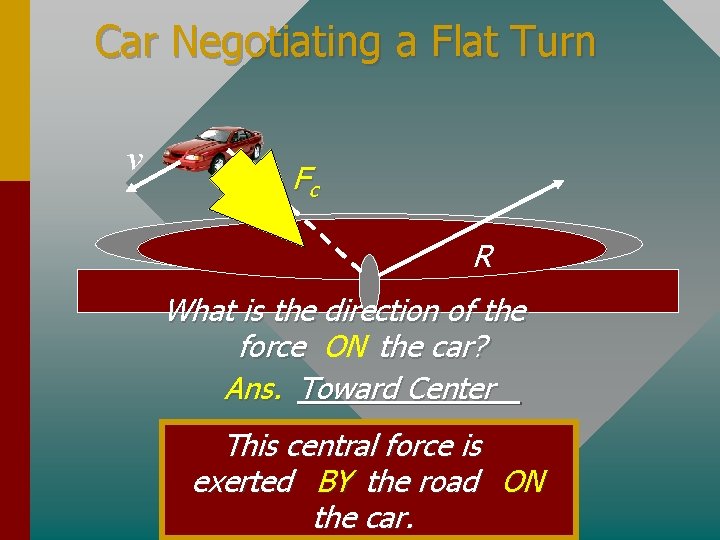
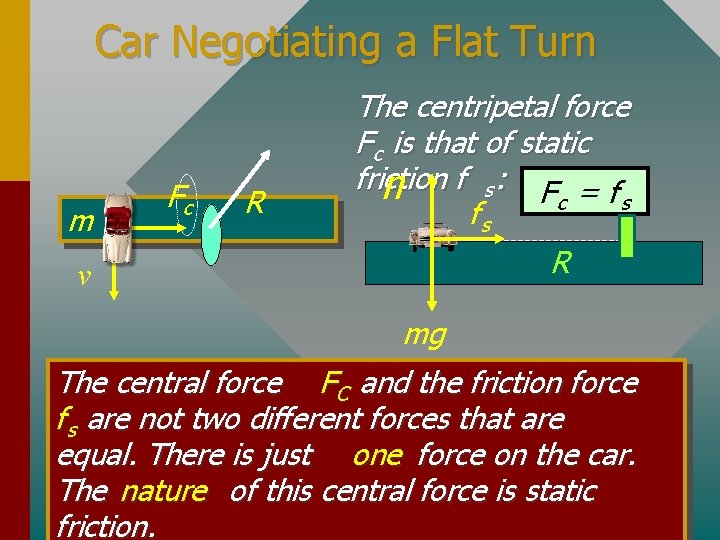
Car Negotiating a Flat Turn v Fc R What is the direction of the force ON the car? Ans. Toward Center This central force is exerted BY the road ON the car.

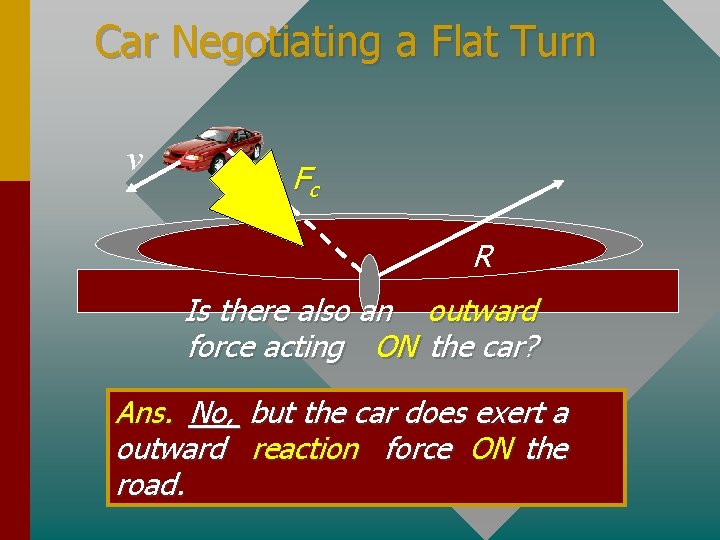
Car Negotiating a Flat Turn v Fc R Is there also an outward force acting ON the car? Ans. No, outward road. but the car does exert a reaction force ON the

Car Negotiating a Flat Turn m Fc R The centripetal force F c is that of static friction n f s: F c = f s fs R v mg The central force F C and the friction force f s are not two different forces that are equal. There is just one force on the car. The nature of this central force is static friction.

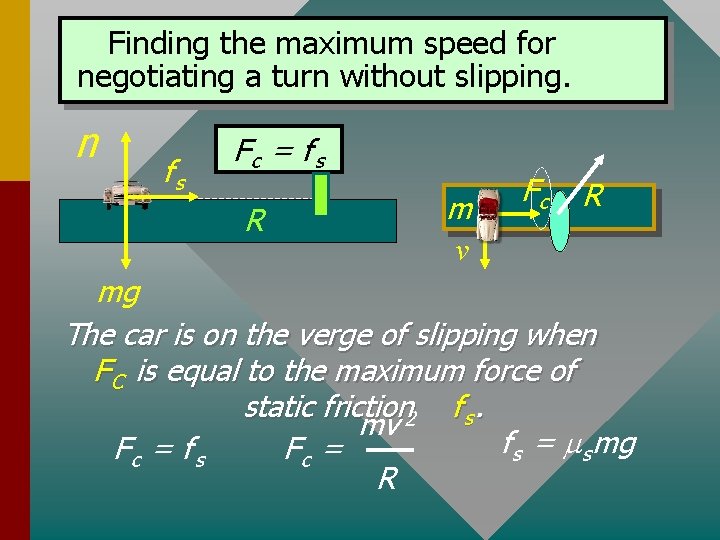
Finding the maximum speed for negotiating a turn without slipping. n fs Fc = f s R m v Fc R mg The car is on the verge of slipping when F C is equal to the maximum force of static friction 2 f s. mv f s = ms mg Fc = f s Fc = R

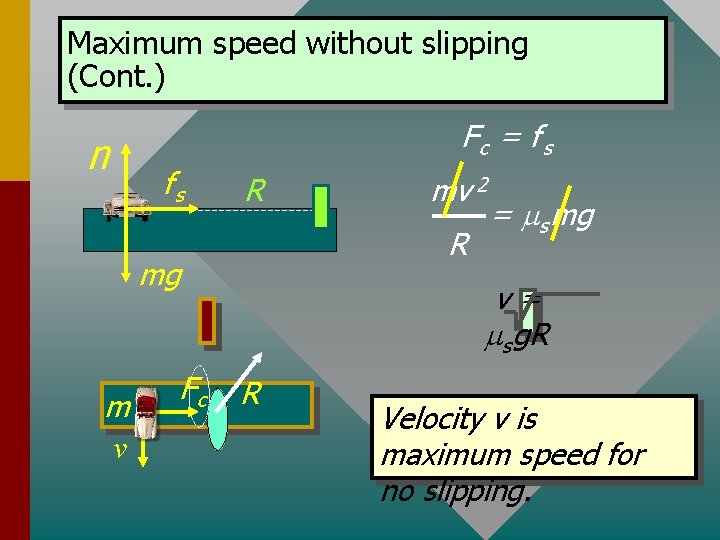
Maximum speed without slipping (Cont. ) n Fc = f s fs R R mg m v Fc mv 2 = ms mg v= ms g. R R Velocity v is maximum speed for no slipping.

Example 4: A car negotiates a turn of radius 70 m when the coefficient of static friction is 0. 7. What is the maximum speed to avoid slipping? m v Fc Fc = R ms = 0. 7 mv 2 R From which: f s = ms mg v= ms g. R g = 9. 8 m/s 2 ; R = 70 m v = 21. 9 m/s

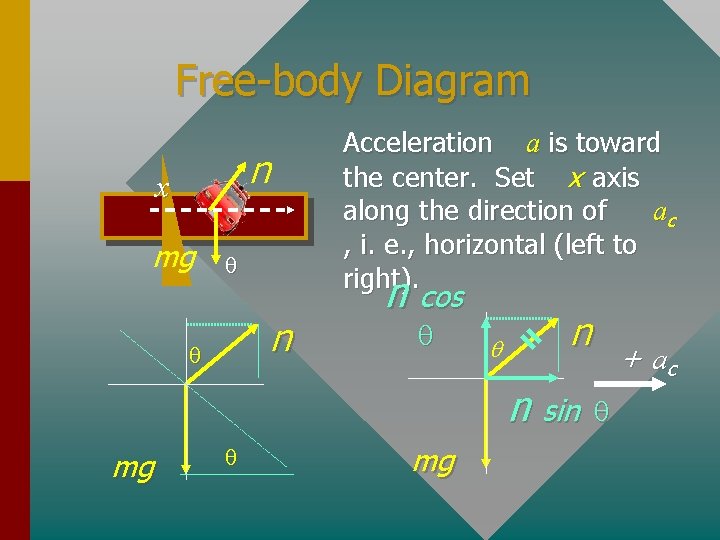
Free-body Diagram Acceleration a is toward the center. Set x axis along the direction of ac , i. e. , horizontal (left to right). n x mg q n cos q q n n sin mg q mg + ac q

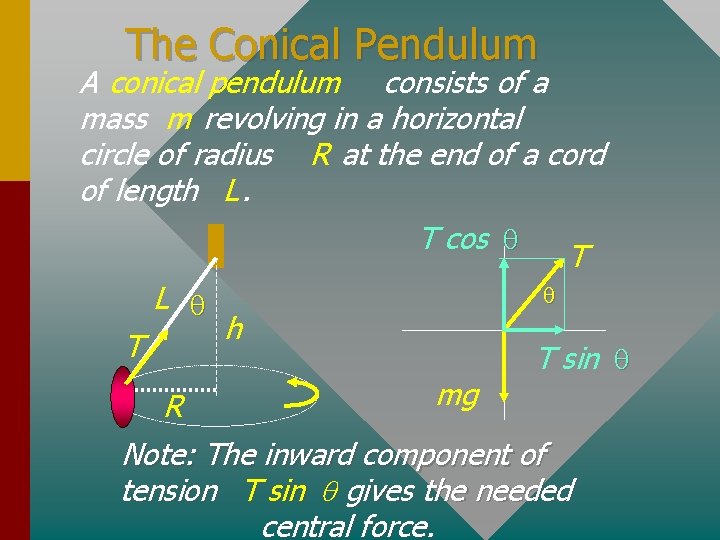
The Conical Pendulum A conical pendulum consists of a mass m revolving in a horizontal circle of radius R at the end of a cord of length L. T cos q L q T R T q h mg T sin q Note: The inward component of tension T sin q gives the needed central force.

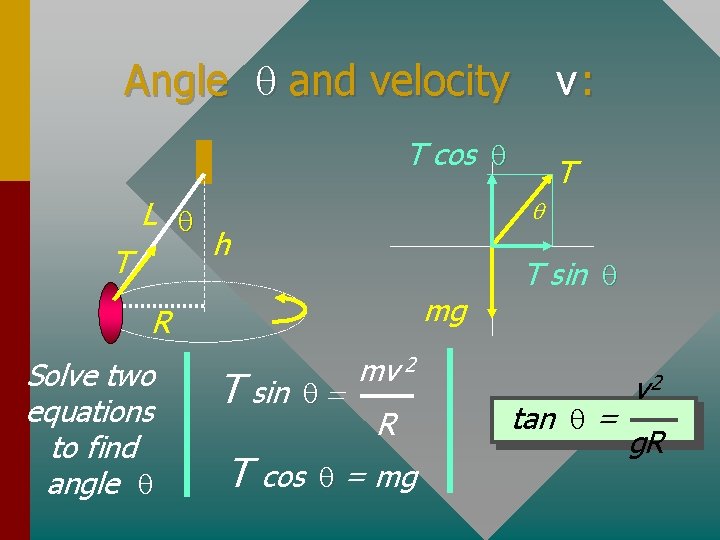
Angle q and velocity v: T cos q L q T q h mg R Solve two equations to find angle q T sin T T q= T sin q mv 2 R cos q = mg tan q = v 2 g. R

Example 6: A 2 -kg mass swings in a horizontal circle at the end of a cord of length 10 m. What is the constant speed of the mass if the rope makes an angle of 30 0 with the vertical? 1. Draw & label sketch. q = 300 2. Recall formula for L q pendulum. h T Find: v = ? R 3. To use this formula, we need to find R 0 = (10 R = L sin 30 R= 5 =? m)(0. 5) m

Example 6(Cont. ): Find v for q = 30 0 4. Use given info to find q = 300 the velocity at 30 0. R = L q R= 5 g = 9. 8 h 2 T m m/ s Solve for R v=? 5 m v = 5. 32 m/s

Example 7: Now find the tension T in the cord if m = 2 kg , q = 30 0 , and L = 10 m. T cos q T q L q h T T sin q 2 kg mg R SF y = 0: T= mg cos q T cos q - mg = 0; = (2 kg)(9. 8 m/s 2 ) cos 30 0 T cos q = mg T = 22. 6 N

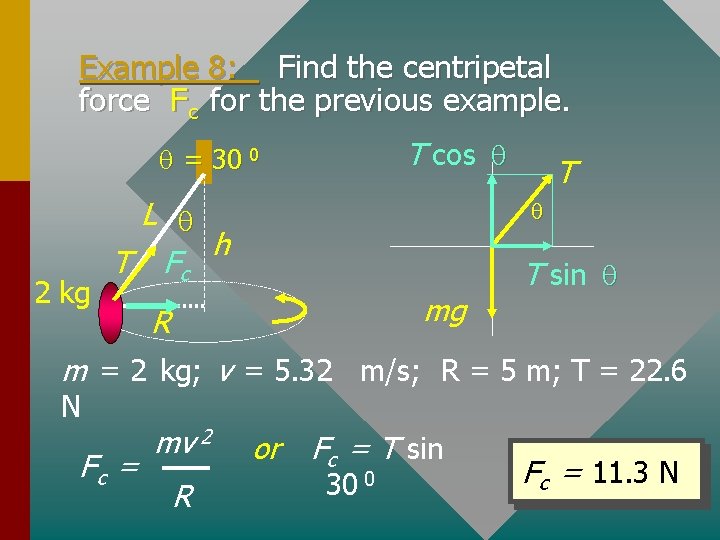
Example 8: Find the centripetal force F c for the previous example. T cos q q = 30 0 2 kg L q h T Fc T q mg R T sin q m = 2 kg; v = 5. 32 m/s; R = 5 m; T = 22. 6 N Fc = mv 2 R or Fc = T sin 30 0 F c = 11. 3 N

Swinging Seats at the Fair This problem is identical to the other examples except for finding R. b L q T h d R=d+b R tan q = R = L sin q + b v 2 g. R and v= g. R tan q

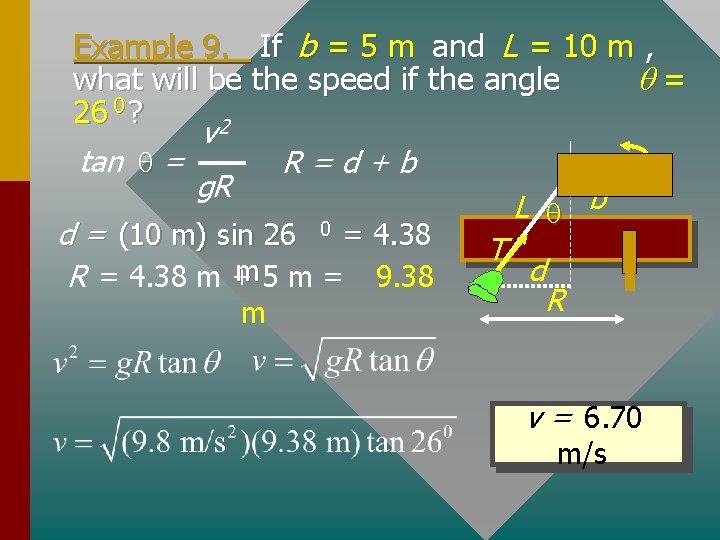
Example 9. If b = 5 m and L = 10 m , what will be the speed if the angle q= 26 0 ? v 2 tan q = R=d+b g. R L q b d = (10 m) sin 26 0 = 4. 38 T m 5 m = 9. 38 d R = 4. 38 m + R m v = 6. 70 m/s

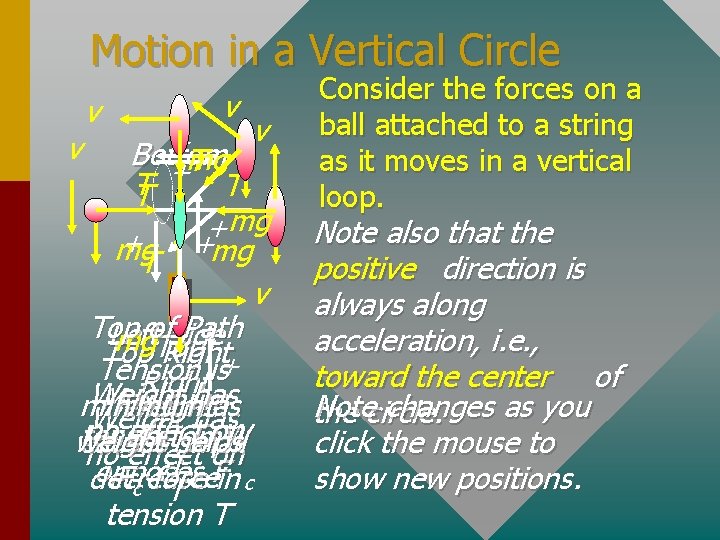
Motion in a Vertical Circle v v v + v Bottom mg T + T T T mg + +mg mg T v Top of. Side Path Left mg Top Right Tension is Right Weight has Maximum minimum as Weight has no Bottom effect tension T, on W weight helps causes small no effect on T opposes Fin c F c force decrease T tension T Consider the forces on a ball attached to a string as it moves in a vertical loop. Note also that the positive direction is always along acceleration, i. e. , toward the center of Note changes as you the circle. click the mouse to show new positions. + +

As an exercise, v + assume that a central 10 N force of F c = 40 N is T required to maintain R circular motion of a T ball and W = 10 N. + v The tension T must 10 adjust so that N central resultant is 40 N. TT = ? _N At top: 10 N + T = 40 = _30 Bottom: N T – 10 N = 40 N T =T 50 =N __? ___

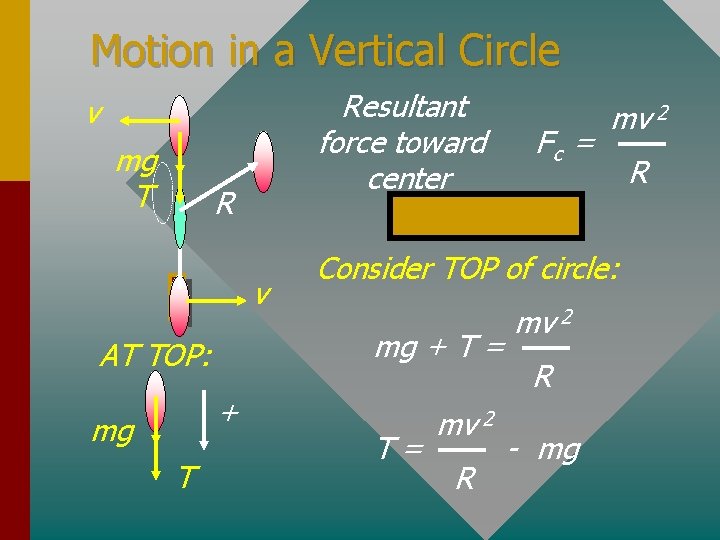
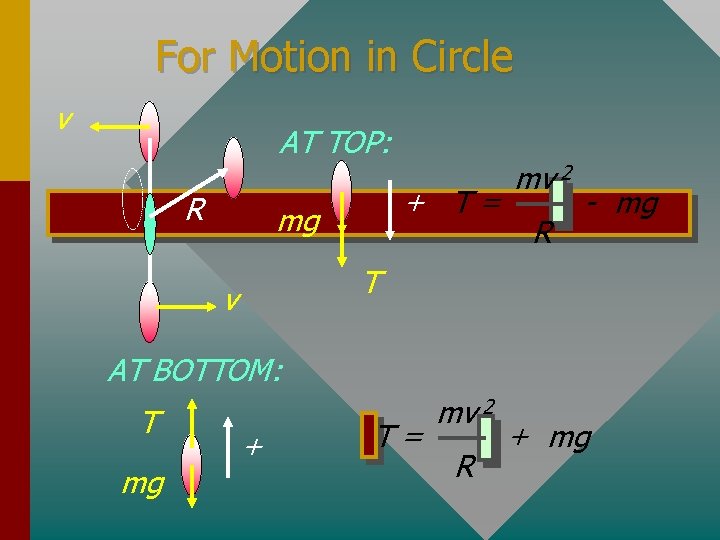
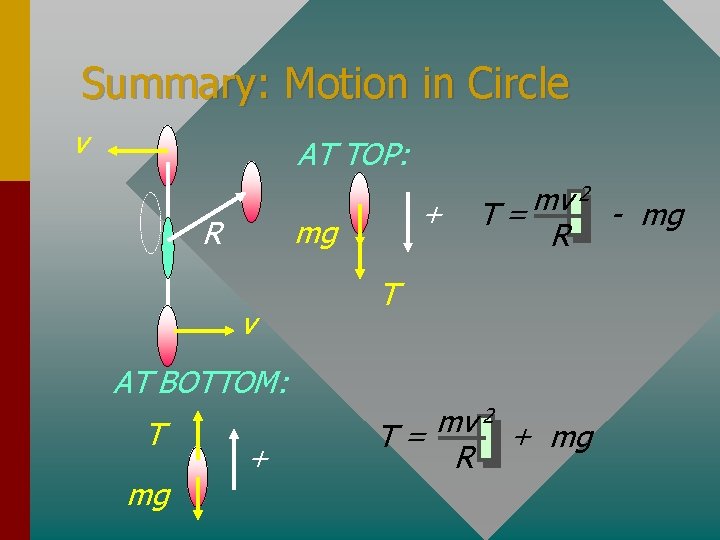
Motion in a Vertical Circle Resultant force toward center v mg T R v + mg T Consider TOP of circle: mg + T = AT TOP: Fc = mv 2 T= mv 2 R - mg R

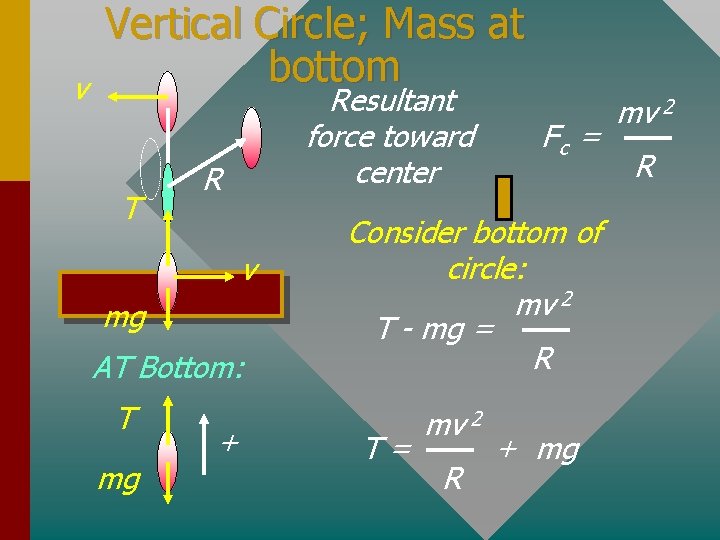
v Vertical Circle; Mass at bottom T Resultant force toward center R v mg AT Bottom: T mg + Fc = Consider bottom of circle: mv 2 T - mg = R T= mv 2 R + mg mv 2 R

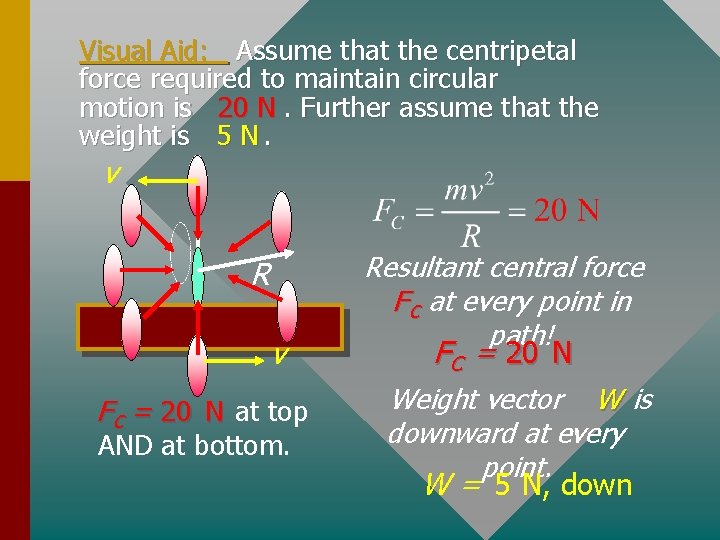
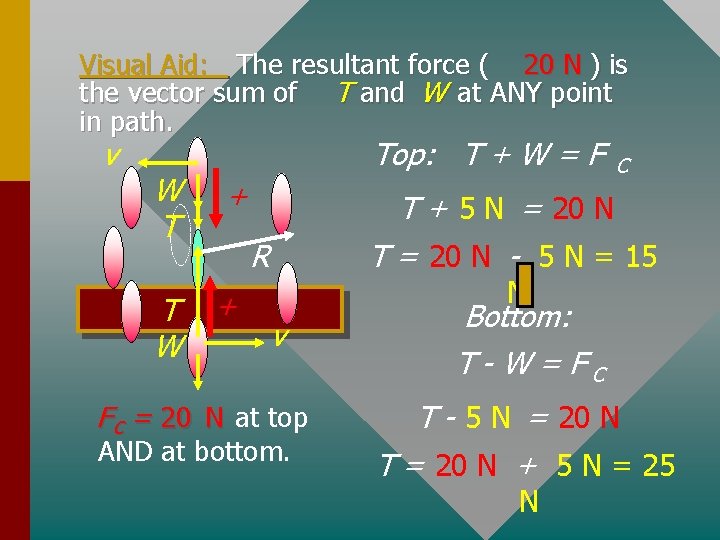
Visual Aid: Assume that the centripetal force required to maintain circular motion is 20 N. Further assume that the weight is 5 N. v R v F C = 20 N at top AND at bottom. Resultant central force F C at every point in path! F C = 20 N Weight vector W is downward at every point. W = 5 N, down

Visual Aid: The resultant force ( 20 N ) is the vector sum of T and W at ANY point in path. W T T W Top: T + W = F + C T + 5 N = 20 N T = 20 N - 5 N = 15 R + v N v F C = 20 N at top AND at bottom. Bottom: T-W=FC T - 5 N = 20 N T = 20 N + 5 N = 25 N

For Motion in Circle v AT TOP: R + T= mg mv 2 R - mg T v AT BOTTOM: T mg + T= mv 2 R + mg

Example 10: A 2 -kg rock swings in a vertical circle of radius 8 m. The speed of the rock as it passes its highest point is 10 m/s. What is tension T in rope? 2 At Top: v mg T T= R mg + T = mv 2 R mv - mg v T = 25 N - 19. 6 N T = 5. 40 N R

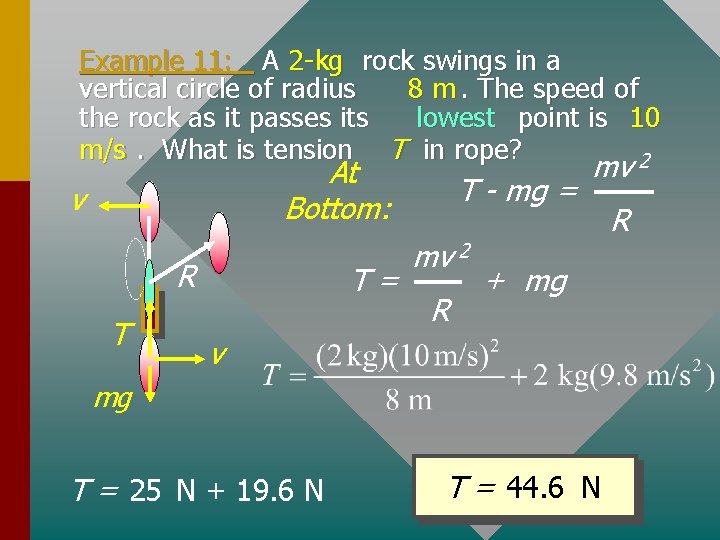
Example 11: A 2 -kg rock swings in a vertical circle of radius 8 m. The speed of the rock as it passes its lowest point is 10 m/s. What is tension T in rope? 2 At Bottom: v R T T= T - mg = mv 2 R mv + mg v mg T = 25 N + 19. 6 N T = 44. 6 N R

Example 12: What is the critical speed v c at the top, if the 2 -kg mass is to continue in a circle of radius 8 m 0? 2 mv v At Top: mg + T = mg R v c occurs when T = 0 R T mv 2 mg = v c = g. R v= m) g. R = (9. 8 m/s 2 )(8 v c = 8. 85 m/s

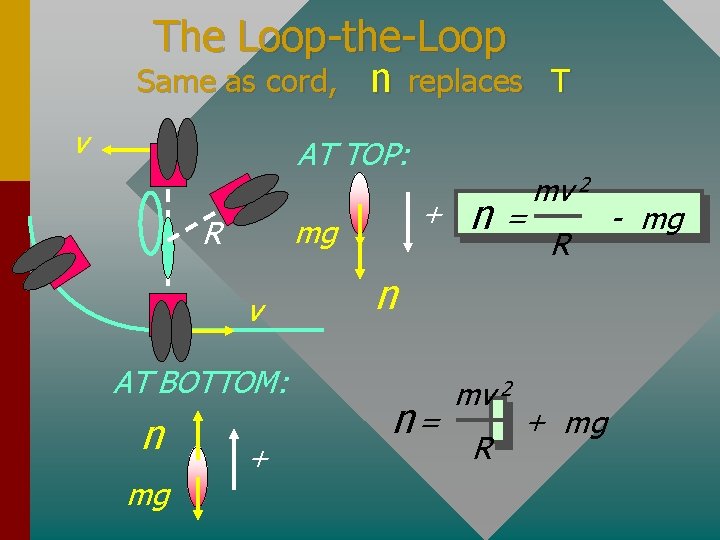
The Loop-the-Loop Same as cord, n replaces v AT TOP: mg R v AT BOTTOM: n mg + + n= T mv 2 R n n= mv 2 R + mg - mg

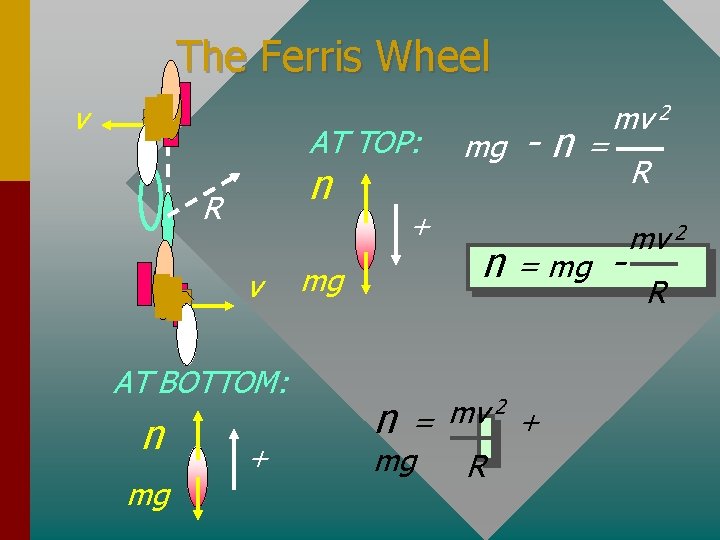
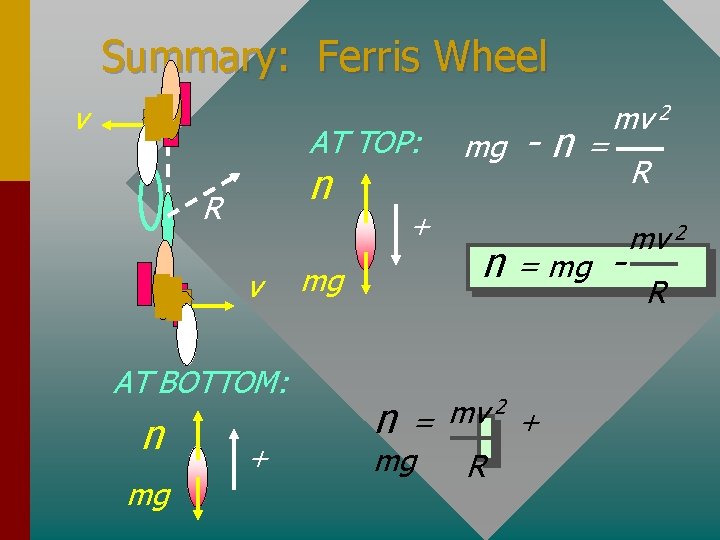
The Ferris Wheel v AT TOP: n R v AT BOTTOM: n mg + mg -n = mv 2 n = mg - 2 mv n= + mg R R mv 2 R

Example 13: What is the apparent weight of a 60 n kg person as she moves v through the highest point m when R = 45 m and the g speed at that point is 6 m/s? Apparent weight will be the normal force at the top: mv 2 mg - n = mg R + R v - mv 2 R n = 540 N

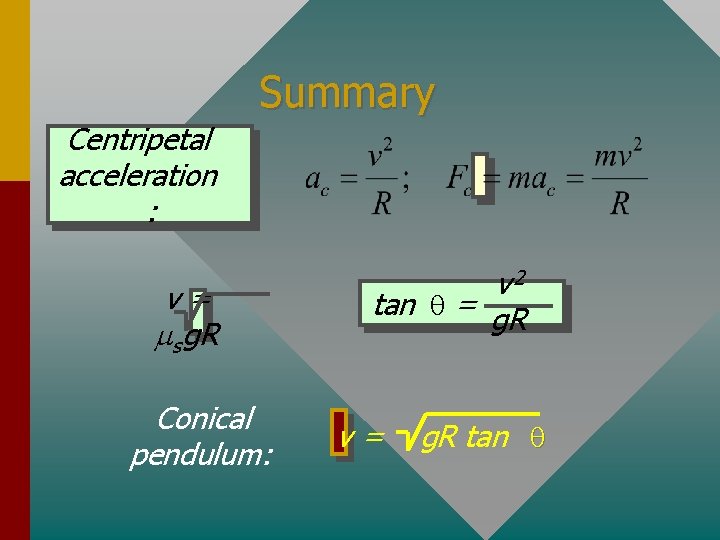
Summary Centripetal acceleration : v= ms g. R Conical pendulum: v 2 tan q = g. R v= g. R tan q

Summary: Motion in Circle v AT TOP: + mg R v 2 mv T= - mg R T AT BOTTOM: T mg + 2 mv T= + mg R

Summary: Ferris Wheel v AT TOP: n R v AT BOTTOM: n mg + mg -n = mv 2 n = mg - 2 mv n= + mg R R mv 2 R

CONCLUSION: Chapter 10 Uniform Circular Motion