Chapter 10 Trees The tree abstract data type

Chapter 10 Trees The tree abstract data type provides a hierarchical structure to the representation of certain types of relationships. ü Array Implementation ü Linked List Implementation ü Binary Search Trees ü Applications ü General Trees CS 240 Chapter 10 – Trees 177

The Binary Tree ADT The binary tree abstract data type is a structure in which entries are configured to have at most two offspring. Root Leaf Node Leaf Binary Tree Leaf The binary aspect of this structure makes it particularly useful in applications where individual choices are needed, making it possible to recursively proceed to the right offspring or to the left offspring of the current node. For example, video games frequently present a player with two options, using a game tree to keep track of the alternatives selected by the player. In addition to constructors and a destructor, the binary tree ADT needs the following functions: • is. Empty - to determine whether the binary tree contains any entries • insert - to insert a new entry at the appropriate location within the tree • traverse - some mechanism to explore the tree CS 240 Chapter 10 – Trees 178

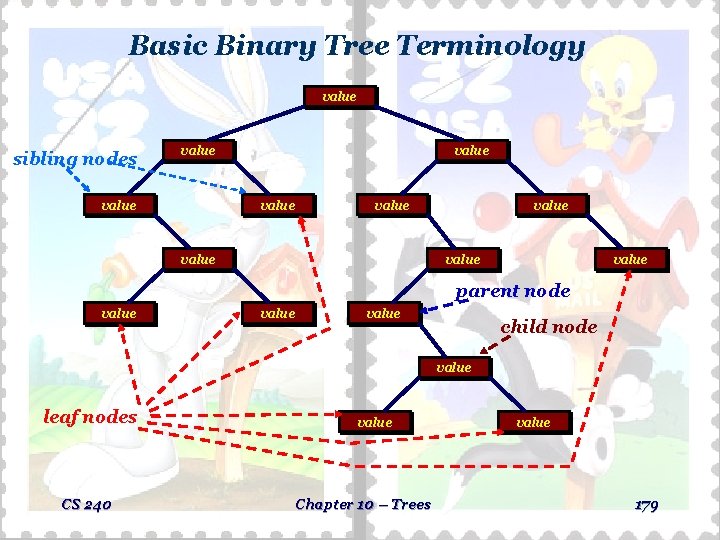
Basic Binary Tree Terminology value sibling nodes value value value parent node value child node value leaf nodes CS 240 value Chapter 10 – Trees value 179

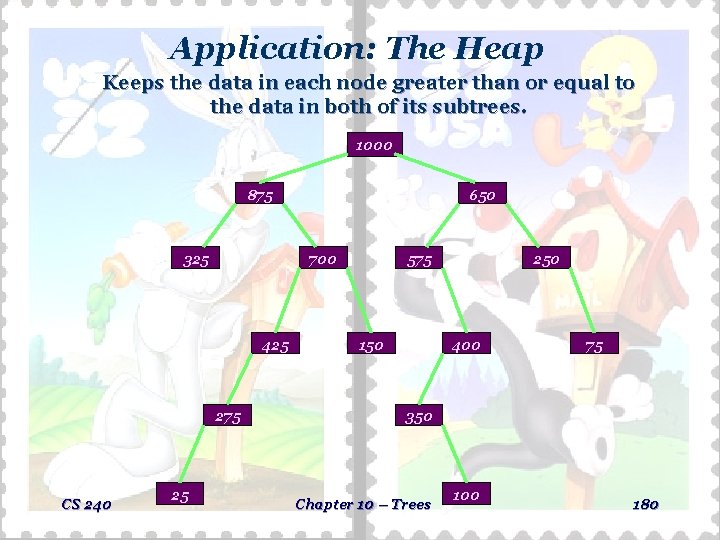
Application: The Heap Keeps the data in each node greater than or equal to the data in both of its subtrees. 1000 875 325 700 425 275 CS 240 25 650 575 150 250 400 75 350 Chapter 10 – Trees 100 180

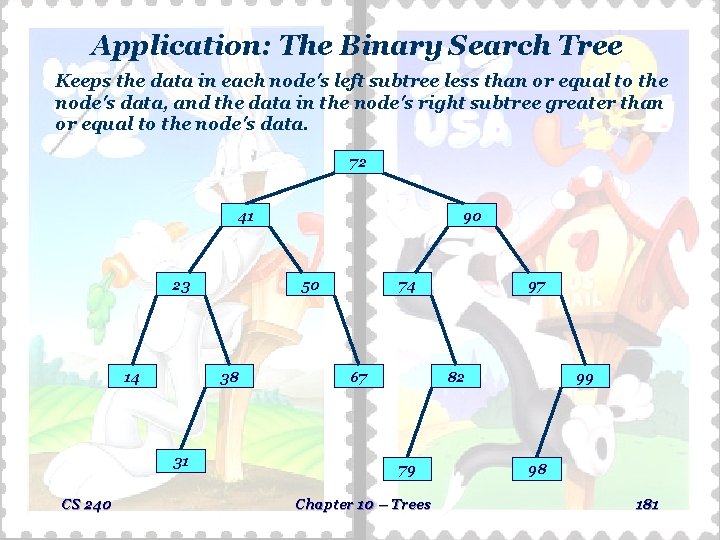
Application: The Binary Search Tree Keeps the data in each node's left subtree less than or equal to the node's data, and the data in the node's right subtree greater than or equal to the node's data. 72 41 23 14 CS 240 50 38 31 90 74 67 97 82 79 Chapter 10 – Trees 99 98 181

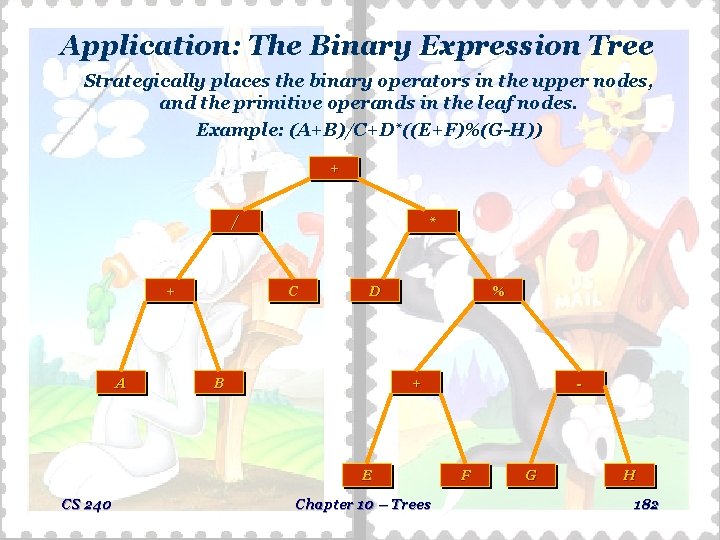
Application: The Binary Expression Tree Strategically places the binary operators in the upper nodes, and the primitive operands in the leaf nodes. Example: (A+B)/C+D*((E+F)%(G-H)) + / + A * C D B % + E CS 240 Chapter 10 – Trees - F G H 182

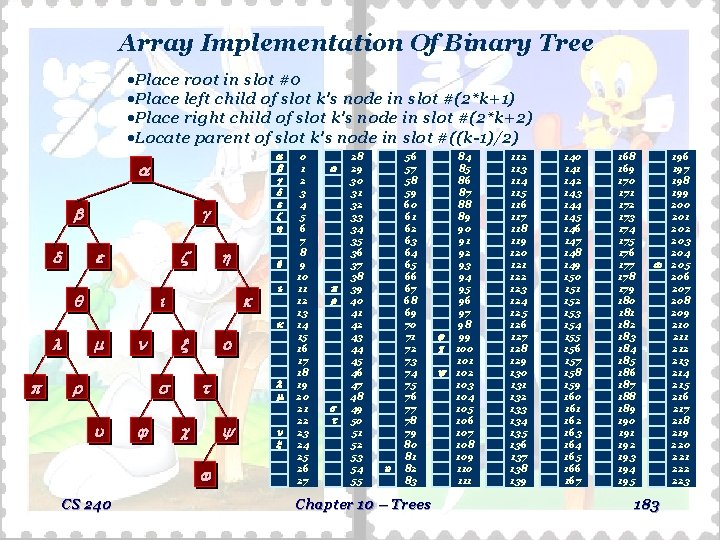
Array Implementation Of Binary Tree ·Place root in slot #0 ·Place left child of slot k's node in slot #(2*k+1) ·Place right child of slot k's node in slot #(2*k+2) ·Locate parent of slot k's node in slot #((k-1)/2) CS 240 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 Chapter 10 – Trees 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 183 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223

Array Implementation Of Binary Tree // Class declaration file: bintree. h // // This file contains the array implementation of the binary tree ADT. // #include <cassert> #include <iostream> #include <iomanip> using namespace std; #ifndef BIN_TREE_H // DECLARATION SECTION FOR THE BINARY TREE CLASS TEMPLATE const int MAX_TREE_NODES = 15; template <class E> class binary_tree { public: // Class constructors binary_tree(); binary_tree(const binary_tree<E> &bt); // Member functions bool is. Empty(); void insert(const E &item); void preorder_traverse(int location); void inorder_traverse(int location); void postorder_traverse(int location); binary_tree<E>& operator = (const binary_tree<E> &bt); void display_array(); CS 240 Chapter 10 – Trees 184

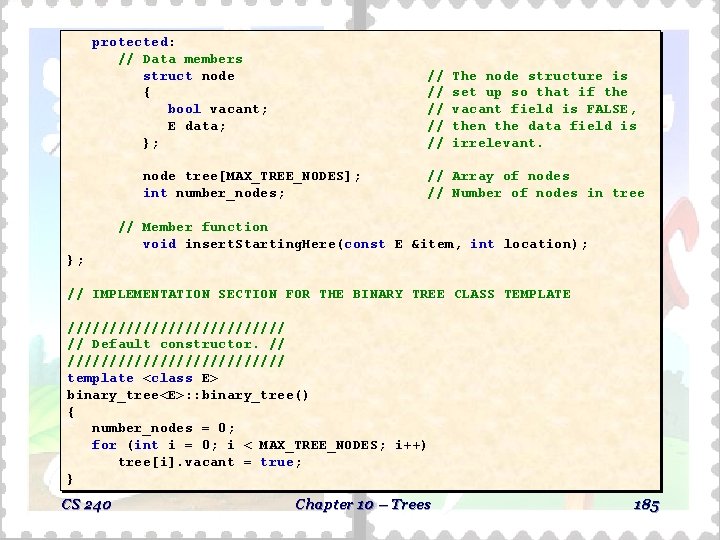
protected: // Data members struct node { bool vacant; E data; }; // // // node tree[MAX_TREE_NODES]; int number_nodes; The node structure is set up so that if the vacant field is FALSE, then the data field is irrelevant. // Array of nodes // Number of nodes in tree // Member function void insert. Starting. Here(const E &item, int location); }; // IMPLEMENTATION SECTION FOR THE BINARY TREE CLASS TEMPLATE ///////////// // Default constructor. // ///////////// template <class E> binary_tree<E>: : binary_tree() { number_nodes = 0; for (int i = 0; i < MAX_TREE_NODES; i++) tree[i]. vacant = true; } CS 240 Chapter 10 – Trees 185

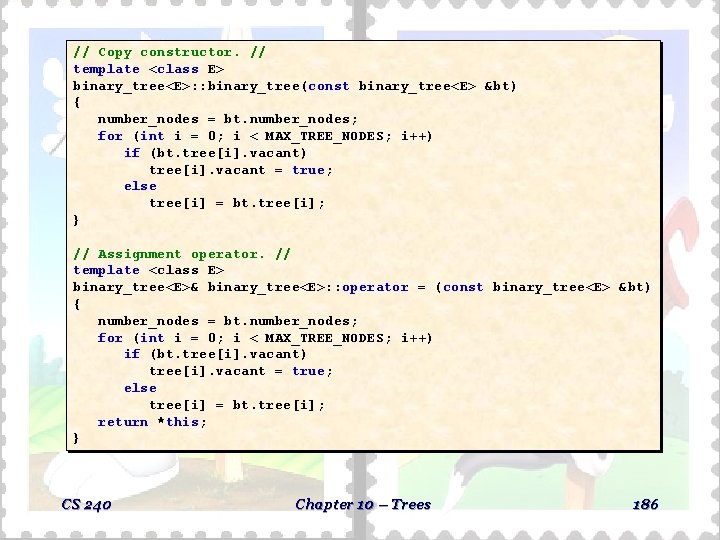
// Copy constructor. // template <class E> binary_tree<E>: : binary_tree(const binary_tree<E> &bt) { number_nodes = bt. number_nodes; for (int i = 0; i < MAX_TREE_NODES; i++) if (bt. tree[i]. vacant) tree[i]. vacant = true; else tree[i] = bt. tree[i]; } // Assignment operator. // template <class E> binary_tree<E>& binary_tree<E>: : operator = (const binary_tree<E> &bt) { number_nodes = bt. number_nodes; for (int i = 0; i < MAX_TREE_NODES; i++) if (bt. tree[i]. vacant) tree[i]. vacant = true; else tree[i] = bt. tree[i]; return *this; } CS 240 Chapter 10 – Trees 186

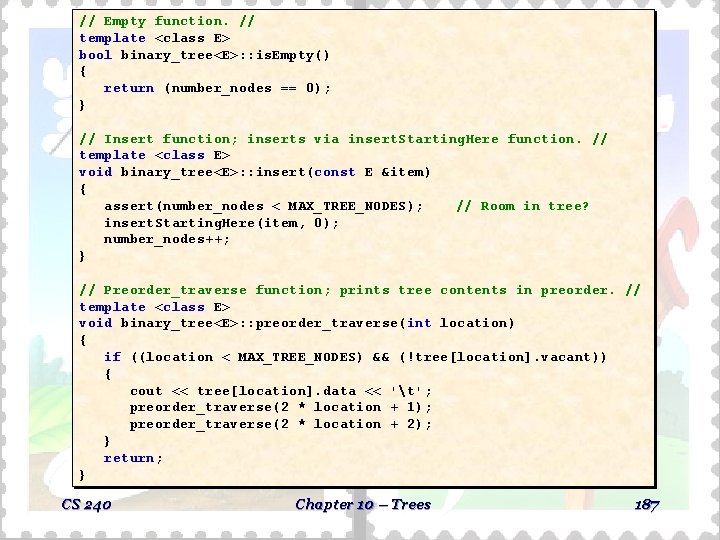
// Empty function. // template <class E> bool binary_tree<E>: : is. Empty() { return (number_nodes == 0); } // Insert function; inserts via insert. Starting. Here function. // template <class E> void binary_tree<E>: : insert(const E &item) { assert(number_nodes < MAX_TREE_NODES); // Room in tree? insert. Starting. Here(item, 0); number_nodes++; } // Preorder_traverse function; prints tree contents in preorder. // template <class E> void binary_tree<E>: : preorder_traverse(int location) { if ((location < MAX_TREE_NODES) && (!tree[location]. vacant)) { cout << tree[location]. data << 't'; preorder_traverse(2 * location + 1); preorder_traverse(2 * location + 2); } return; } CS 240 Chapter 10 – Trees 187

///////////////////////////////// // Inorder_traverse function; prints tree contents in inorder. // ///////////////////////////////// template <class E> void binary_tree<E>: : inorder_traverse(int location) { if ((location < MAX_TREE_NODES) && (!tree[location]. vacant)) { inorder_traverse(2 * location + 1); cout << tree[location]. data << 't'; inorder_traverse(2 * location + 2); } return; } /////////////////////////////////// // Postorder_traverse function; prints tree contents in postorder. // /////////////////////////////////// template <class E> void binary_tree<E>: : postorder_traverse(int location) { if ((location < MAX_TREE_NODES) && (!tree[location]. vacant)) { postorder_traverse(2 * location + 1); postorder_traverse(2 * location + 2); cout << tree[location]. data << 't'; } return; } CS 240 Chapter 10 – Trees 188

// Display_array function; prints tree contents as an // // array, printing the word vacant if a node is vacant. // template <class E> void binary_tree<E>: : display_array() { int index; for (int i = 0; i < MAX_TREE_NODES/5; i++) { for (int j = 0; j < 5; j++) { index = (MAX_TREE_NODES/5)*j+i; cout << setw(2) << index << " = "; if (tree[index]. vacant) cout << setw(6) << "vacant" << setw(3) << ""; else cout << setw(6) << tree[index]. data << setw(3) << ""; } cout << endl; } } CS 240 Chapter 10 – Trees 189

//////////////////////////////// // Insert. Starting. Here function; inserts item into tree using // // ordering (i. e. , inserting smaller values to the left and // // larger values to the right). // //////////////////////////////// template <class E> void binary_tree<E>: : insert. Starting. Here(const E &item, int location) { assert(location < MAX_TREE_NODES); // Must be legitimate // array index if (tree[location]. vacant) { tree[location]. data = item; tree[location]. vacant = false; } else if (item < tree[location]. data) insert. Starting. Here(item, 2 * location + 1); else insert. Starting. Here(item, 2 * location + 2); } #define BIN_TREE_H #endif CS 240 Chapter 10 – Trees 190

Example Driver For The Array Implementation // Program file: treedriv. cpp // // This program illustrates the // // creation of a binary tree. // #include <iostream> #include "bintree. h" using namespace std; void print_tree(binary_tree<int> &tree); // The main function queries the // // user for new tree elements. // void main() { binary_tree<int> tree; int number; cout << "Enter a number: "; cin >> number; while (number > 0) { tree. insert(number); tree. display_array(); cout << "Enter a number: "; cin >> number; } CS 240 print_tree(tree); } // The print_tree function outputs // // the final contents of the tree, // // first by displaying the entire // // array, then by printing out the // // non-vacant tree elements in in- // // order, preorder, and postorder. // void print_tree(binary_tree<int> &tree) { cout << "Array contents: n"; tree. display_array(); cout << “n. Inorder traversal: n"; tree. inorder_traverse(0); cout << “n. Preorder traversal: n"; tree. preorder_traverse(0); cout << “n. Postorder traversal: n"; tree. postorder_traverse(0); cout << endl; } Chapter 10 – Trees 191

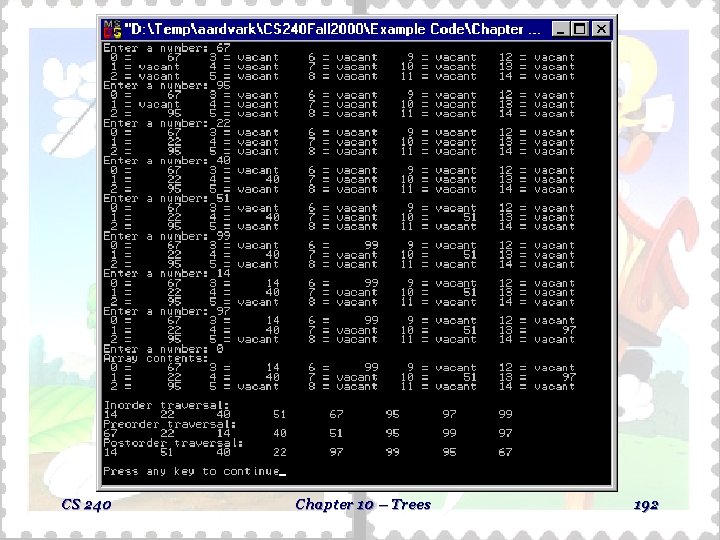
CS 240 Chapter 10 – Trees 192

A Good Use For The Array Implementation: Heaps // Class declaration file: heap. h // // This file contains the array implementation of the heap ADT. // #include "bintree. h" #include <cassert> #include <iostream> using namespace std; #ifndef HEAP_H // DECLARATION SECTION FOR THE HEAP CLASS TEMPLATE template <class E> class heap: public binary_tree<E> { public: // Class constructors heap(); heap(const heap<E> &h); // Member functions void insert(const E &item); heap<E>& operator = (const heap<E> &h); }; CS 240 Chapter 10 – Trees 193

// IMPLEMENTATION SECTION FOR // THE HEAP CLASS TEMPLATE ///////////// // Default constructor. // ///////////// template <class E> heap<E>: : heap(): binary_tree<E>() { } ///////////// // Assignment operator. // ///////////// template <class E> heap<E>& heap<E>: : operator = (const heap<E> &h) { number_nodes = h. number_nodes; for (int i=0; i<MAX_TREE_NODES; ++i) { if (h. tree[i]. vacant) tree[i]. vacant = true; else tree[i] = h. tree[i]; } return *this; } //////////// // Copy constructor. // //////////// template <class E> heap<E>: : heap(const heap<E> &h) { number_nodes = h. number_nodes; for (int i=0; i<MAX_TREE_NODES; ++i) { if (h. tree[i]. vacant) tree[i]. vacant = true; else tree[i] = h. tree[i]; } } CS 240 Chapter 10 – Trees 194

///////////////////////////////////// // Insert function; inserts into the heap to retain the heap structure // // and to ensure non-fragmentation of the array structure, moving low // // elements down when a high element is inserted. // ///////////////////////////////////// template <class E> void heap<E>: : insert(const E &item) { int location, parent; assert(number_nodes < MAX_TREE_NODES); // Now walk the new item up the tree, starting at location = number_nodes; parent = (location-1) / 2; while ((location > 0) && (tree[parent]. data < item)) { tree[location] = tree[parent]; location = parent; parent = (location-1) / 2; } tree[location]. data = item; tree[location]. vacant = false; number_nodes++; } #define HEAP_H #endif CS 240 Chapter 10 – Trees 195

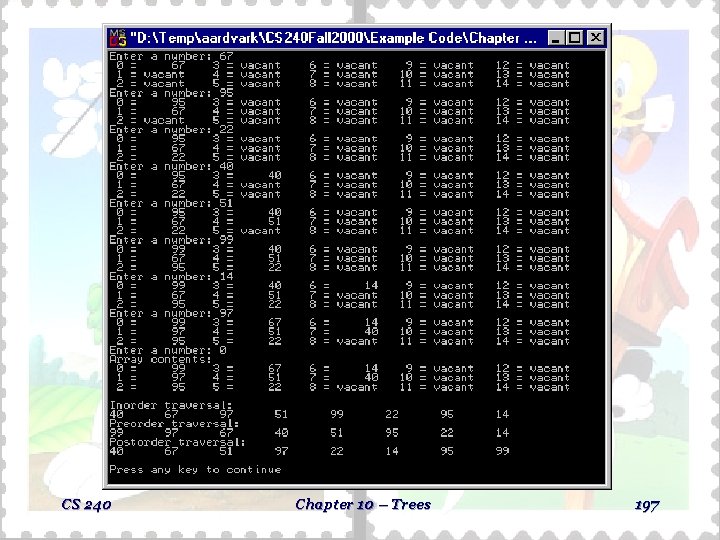
Example Driver For The Heap Implementation // Program file: heapdriv. cpp // // This program illustrates // // the creation of a heap. // #include <iostream> #include "heap. h" using namespace std; void print_heap(heap<int> &tree); // The main function queries the // // user for new heap elements. // void main() { heap<int> tree; int number; cout << "Enter a number: "; cin >> number; while (number > 0) { tree. insert(number); tree. display_array(); cout << "Enter a number: "; cin >> number; } print_heap(tree); // The print_heap function outputs // // the final contents of the heap, // // first by displaying the entire // // array, then by printing out the // // non-vacant heap elements in in- // // order, preorder, and postorder. // void print_heap(heap<int> &tree) { cout << "Array contents: n"; tree. display_array(); cout << "n. Inorder traversal: n"; tree. inorder_traverse(0); cout << " n. Preorder traversal: n"; tree. preorder_traverse(0); cout << " n. Postorder traversal: n"; tree. postorder_traverse(0); cout << endl; } } CS 240 Chapter 10 – Trees 196

CS 240 Chapter 10 – Trees 197

Linked List Implementation Of Binary Tree // Class declaration file: bintree. h // This file contains the array implementation of the binary tree ADT. // #ifndef BIN_TREE_H #include <stdlib> #include <cassert> #include <fstream> #include <iomanip> using namespace std; // DECLARATION SECTION FOR LINKED VERSION OF BINARY TREE template <class E> class binary_tree { public: // Class constructors and destructor binary_tree(); binary_tree(const binary_tree<E> &bt); ~binary_tree(); // Member functions bool is. Empty() const; void insert(const E &item); void preorder. Traverse(ofstream &os) const; void inorder. Traverse(ofstream &os) const; void postorder. Traverse(ofstream &os) const; binary_tree<E>& operator = (const binary_tree<E> &bt); CS 240 Chapter 10 – Trees 198

protected: // Data members struct node; typedef node* node_ptr; struct node { E data; node_ptr left; node_ptr right; }; node_ptr root; // Member functions node_ptr get_node(const E &data); void insert. Into. Tree(node_ptr &tree. Root, const E &data); void copy. Tree(node_ptr tree. Root) const; void destroy. Tree(node_ptr tree. Root); void preorder. Output(node_ptr tree. Root, ofstream &os) const; void inorder. Output(node_ptr tree. Root, ofstream &os) const; void postorder. Output(node_ptr tree. Root, ofstream &os) const; }; CS 240 Chapter 10 – Trees 199

// IMPLEMENTATION SECTION FOR LINKED VERSION OF BINARY TREE // Default constructor. // template <class E> binary_tree<E>: : binary_tree() { root = NULL; } // Copy constructor. // template <class E> binary_tree<E>: : binary_tree(const binary_tree<E> &bt) { root = NULL; copy. Tree(bt. root); } // Assignment operator. // template <class E> binary_tree<E>& binary_tree<E>: : operator = (const binary_tree<E> &bt) { root = NULL; copy. Tree(bt. root); return *this; } CS 240 Chapter 10 – Trees 200

// Function copy. Tree: Starting at the node pointed to by // parameter tree. Root, this function recursively copies the // elements of an existing tree into the *this tree. By // proceeding in a preorder fashion, this function ensures // that the elements of *this will correspond exactly (in // value and position) to the elements of the existing tree. template <class E> void binary_tree<E>: : copy. Tree(node_ptr tree. Root) const { if (tree. Root != NULL) { insert(tree. Root->data); copy. Tree(tree. Root->left); copy. Tree(tree. Root->right); } } // // Destructor. // template <class E> binary_tree<E>: : ~binary_tree() { destroy. Tree(root); root = NULL; } CS 240 Chapter 10 – Trees 201

// Function destroy. Tree: returns all memory associated with // // the tree to the system heap, by recursively destroying // // the two subtrees and then deleting the root. // template <class E> void binary_tree<E>: : destroy. Tree(node_ptr tree. Root) { if (tree. Root != NULL) { destroy. Tree(tree. Root->left); destroy. Tree(tree. Root->right); delete tree. Root; } } // Empty function. // template <class E> bool binary_tree<E>: : is. Empty() const { return root == NULL; } CS 240 Chapter 10 – Trees 202

// Insert function. // template <class E> void binary_tree<E>: : insert(const E &item) { insert. Into. Tree(root, item); } // Function insert. Into. Tree: recursively inserts parameter // // item into tree using binary search tree assumption. // template <class E> void binary_tree<E>: : insert. Into. Tree(node_ptr &tree. Root, const E &item) { if (tree. Root == NULL) tree. Root = get_node(item); else if (item < tree. Root->data) insert. Into. Tree(tree. Root->left, item); else insert. Into. Tree(tree. Root->right, item); } CS 240 Chapter 10 – Trees 203

// Function preorder. Traverse. // template <class E> void binary_tree<E>: : preorder. Traverse(ofstream &os) const { preorder. Output(root, os); } // Function preorder. Output: Outputs contents of // // the tree into parameterized file by recursively // // traversing the tree in preorder. // template <class E> void binary_tree<E>: : preorder. Output(node_ptr tree. Root, ofstream &os) const { if (tree. Root != NULL) { os << tree. Root->data << endl; preorder. Output(tree. Root->left, os); preorder. Output(tree. Root->right, os); } } CS 240 Chapter 10 – Trees 204

// Function inorder. Traverse. // template <class E> void binary_tree<E>: : inorder. Traverse(ofstream &os) const { inorder. Output(root, os); } // Function inorder. Output: Outputs contents of // // the tree into parameterized file by recursively // // traversing the tree in inorder. // template <class E> void binary_tree<E>: : inorder. Output(node_ptr tree. Root, ofstream &os) const { if (tree. Root != NULL) { inorder. Output(tree. Root->left, os); os << tree. Root->data << endl; inorder. Output(tree. Root->right, os); } } CS 240 Chapter 10 – Trees 205

// Function postorder. Traverse. // template <class E> void binary_tree<E>: : postorder. Traverse(ofstream &os) const { postorder. Output(root, os); } // Function postorder. Output: Outputs contents of // // the tree into parameterized file by recursively // // traversing the tree in postorder. // template <class E> void binary_tree<E>: : postorder. Output(node_ptr tree. Root, ofstream &os) const { if (tree. Root != NULL) { postorder. Output(tree. Root->left, os); postorder. Output(tree. Root->right, os); os << tree. Root->data << endl; } } CS 240 Chapter 10 – Trees 206

// Function get_node: Dynamically allocates space for a new // // tree node, placing the parameter item's value into the // // new node, and initializing both of its pointers to NULL. // template <class E> typename binary_tree<E>: : node_ptr binary_tree<E>: : get_node(const E &item) { node_ptr temp = new node; assert(temp != NULL); temp->data = item; temp->left = NULL; temp->right = NULL; return temp; } #define BIN_TREE_H #endif CS 240 Chapter 10 – Trees 207

Example Driver For The Linked List Implementation // Program file: testtree. cpp // // // This program illustrates working with a binary tree. The input consists of an unordered list of integers from a file. The output consists of three files containing the preorder, inorder, and postorder traversals of the binary search tree that is constructed from the input integers. input_file. open("numbers. txt"); pre_file. open("preordered. txt"); in_file. open("inordered. txt"); post_file. open("postordered. txt"); input_file >> number; while (!input_file. eof()) { tree. insert(number); input_file >> number; } input_file. close(); #include <iostream> #include <fstream> #include "bintree. h" using namespace std; void main() { int number; ifstream input_file; ofstream pre_file; ofstream in_file; ofstream post_file; binary_tree<int> tree; tree. preorder. Traverse(pre_file); tree. inorder. Traverse(in_file); tree. postorder. Traverse(post_file); pre_file. close(); in_file. close(); post_file. close(); return; } CS 240 Chapter 10 – Trees 208

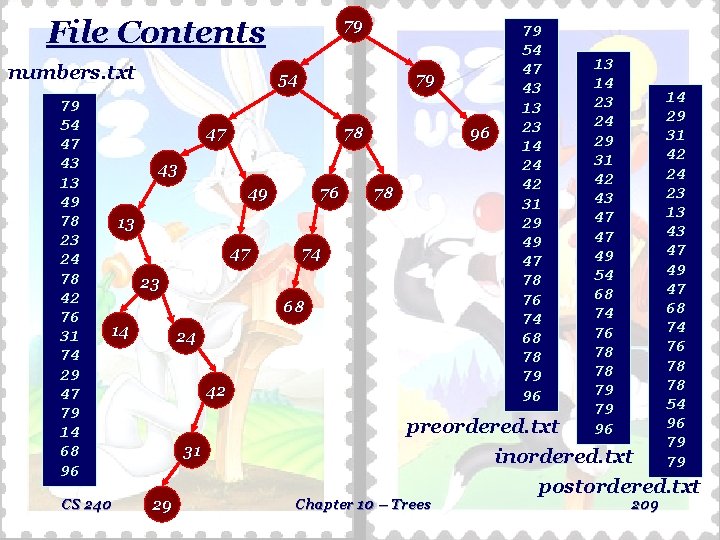
File Contents numbers. txt 79 54 47 43 13 49 78 23 24 78 42 76 31 74 29 47 79 14 68 96 79 54 79 47 78 96 43 49 76 78 13 47 74 23 68 14 CS 240 24 42 79 54 47 43 13 23 14 24 42 31 29 49 47 78 76 74 68 78 79 96 preordered. txt 31 29 Chapter 10 – Trees 13 14 23 24 29 31 42 43 47 47 49 54 68 74 76 78 78 79 79 96 14 29 31 42 24 23 13 43 47 49 47 68 74 76 78 78 54 96 79 79 inordered. txt postordered. txt 209

New Recursive Traversal Member Function // Kick off the recursion to count the binary tree’s pairs of “twins” // (i. e. , the number of offspring pairs with identical values). template <class E> int binary_tree<E>: : twin. Traverse() { return twin. Count(root); } // Recursive member function to determine the number of twin offspring // pairs, starting with the subtree rooted at the parameter tree. Root. template <class E> int binary_tree<E>: : twin. Count(node_ptr tree. Root) { if (tree. Root == NULL) return 0; else if ((tree. Root->left != NULL) && (tree. Root->right != NULL) && (tree. Root->left->data == tree. Root->right->data)) return (1 + twin. Count(tree. Root->left) + twin. Count(tree. Root->right)); else return (twin. Count(tree. Root->left) + twin. Count(tree. Root->right)); } CS 240 Chapter 10 – Trees 210

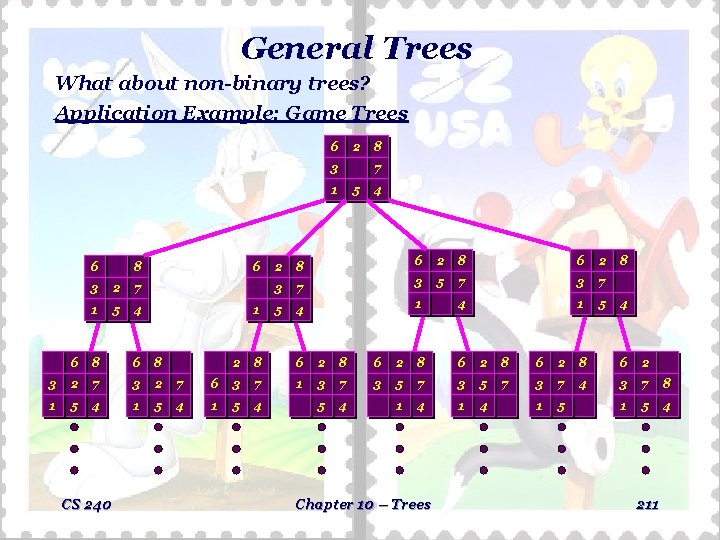
General Trees What about non-binary trees? Application Example: Game Trees 6 2 3 7 1 6 8 3 2 7 1 5 4 6 1 6 8 3 2 7 1 5 4 CS 240 8 5 4 6 2 8 6 2 7 3 5 7 3 7 4 1 5 2 8 3 5 8 4 2 8 6 2 8 6 2 6 3 7 1 3 7 3 5 7 3 7 4 3 7 8 1 5 4 1 4 1 5 4 Chapter 10 – Trees 211

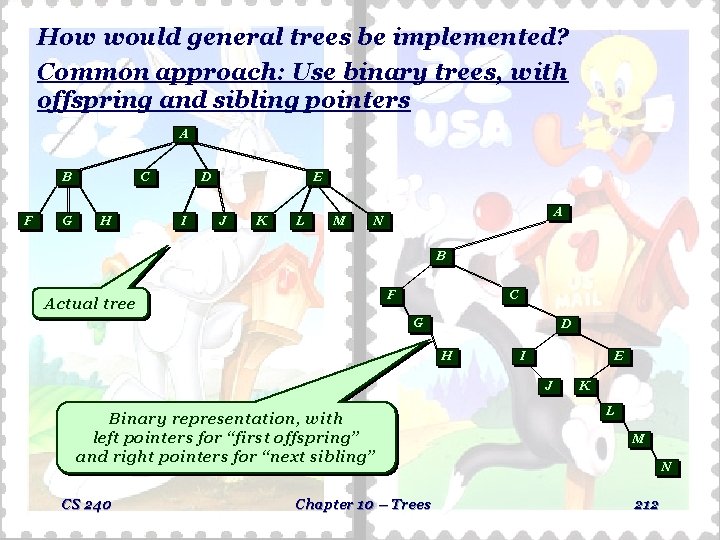
How would general trees be implemented? Common approach: Use binary trees, with offspring and sibling pointers A B F G C H D I E J K L M A N B F Actual tree C G D H I E J Binary representation, with left pointers for “first offspring” and right pointers for “next sibling” CS 240 Chapter 10 – Trees K L M N 212