Chapter 10 Transportation and Assignment Models To accompany

Chapter 10 Transportation and Assignment Models To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 10 -1 1

Learning Objectives Students will be able to • Structure special LP problems using the transportation and assignment models. • Use the N. W. corner, VAM, MODI, and stepping-stone method. • Solve facility location and other application problems with transportation methods. • Solve assignment problems with the Hungarian (matrix reduction) method To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 10 -2 2

Chapter Outline 10. 1 Introduction 10. 2 Setting Up a Transportation Problem 10. 2 Developing an Initial Solution: Northwest Corner Rule 10. 4 Stepping-Stone Method: Finding a Least-Cost Solution 10. 5 MODI Method 10. 6 Vogel’s Approximation Method 10. 7 Unbalanced Transportation Problems To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 10 -3 3

Chapter Outline continued 10. 8 Degeneracy in Transportation Problems 10. 9 More Than One Optimal Solution 10. 10 Maximization Transportation Problems 10. 11 Unacceptable or Prohibited Routes 10. 12 Facility Location Analysis 10. 13 Approach of the Assignment Model 10. 14 Unbalanced Assignment Models 10. 15 Maximization Assignment Problems To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 10 -4 4

Specialized Problems • Transportation Problem • Distribution of items from several sources to several destinations. Supply capacities and destination requirements known. • Assignment Problem • One-to-one assignment of people to jobs, etc. Specialized algorithms save time! To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 10 -5 5

Importance of Special Purpose Algorithms • Fewer, less complicated, computations than with simplex • Less computer memory required • Produce integer solutions To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 10 -6 6

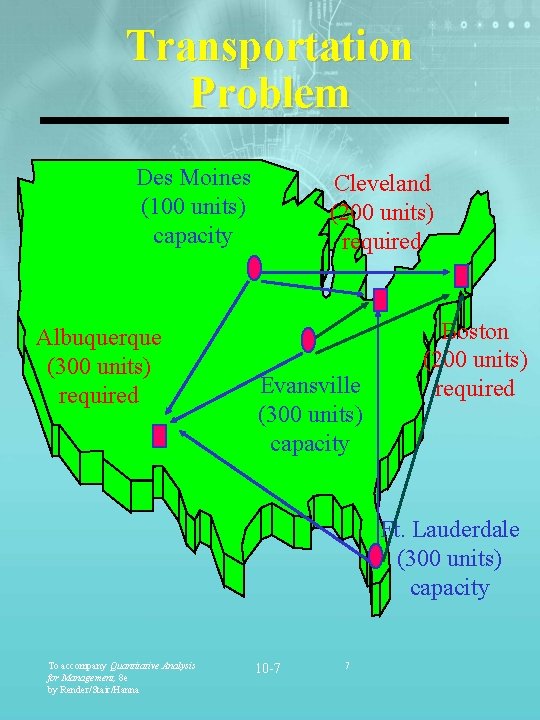
Transportation Problem Des Moines (100 units) capacity Albuquerque (300 units) required Cleveland (200 units) required Evansville (300 units) capacity Boston (200 units) required Ft. Lauderdale (300 units) capacity To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 10 -7 7

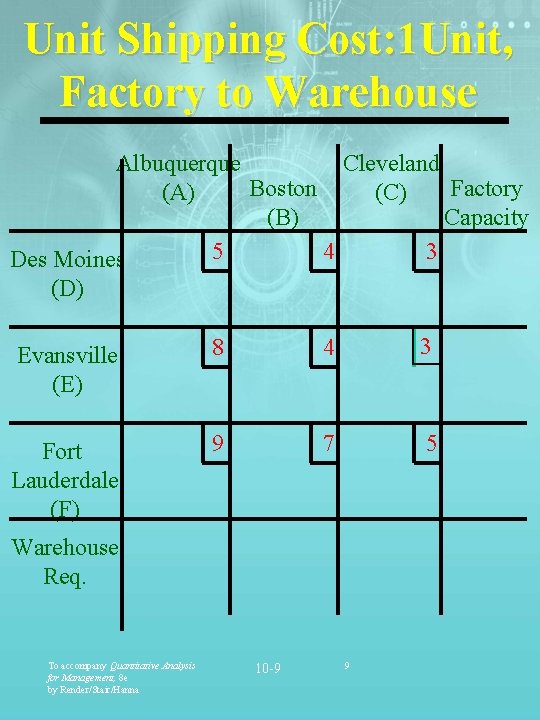
Transportation Costs To (Destinations) From (Sources) Albuquerque Cleveland Boston Des Moines $5 $4 $3 Evansville $8 $4 $3 Fort Lauderdale $9 $7 $5 To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 10 -8 8

Unit Shipping Cost: 1 Unit, Factory to Warehouse Albuquerque Cleveland Boston Factory (A) (C) (B) Capacity 5 4 3 Des Moines (D) Evansville (E) 8 4 3 Fort Lauderdale (F) 9 7 5 Warehouse Req. To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 10 -9 9

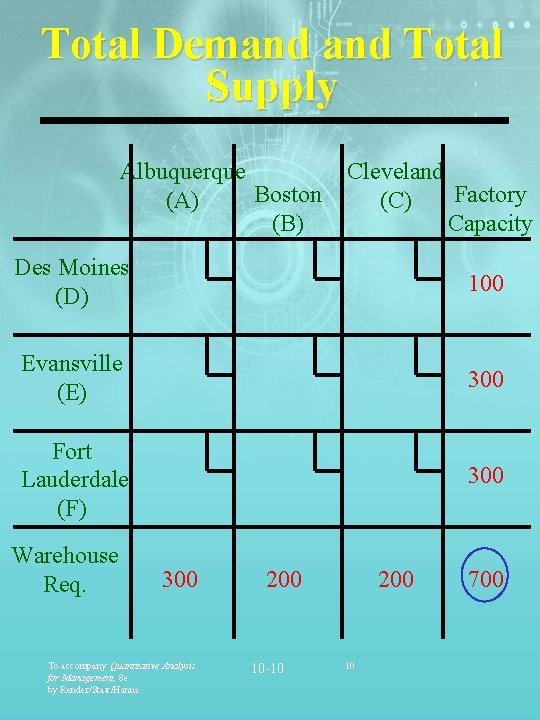
Total Demand Total Supply Albuquerque Boston (A) (B) Cleveland Factory (C) Capacity Des Moines (D) 100 Evansville (E) 300 Fort Lauderdale (F) 300 Warehouse Req. 300 To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 200 10 -10 200 10 700

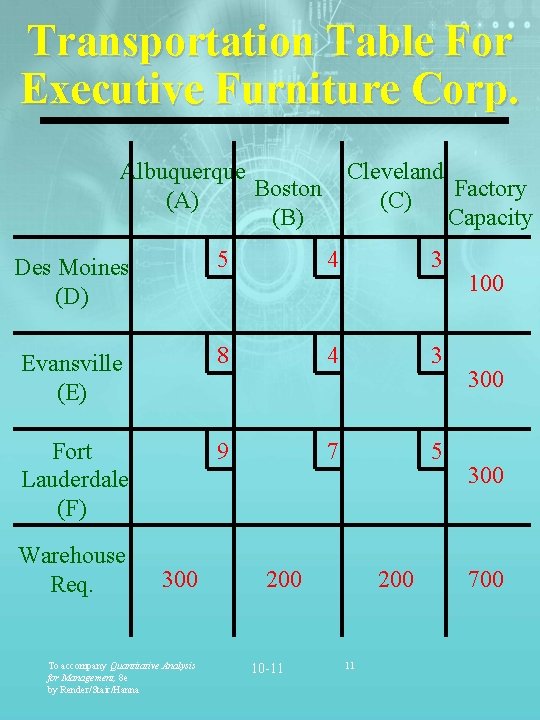
Transportation Table For Executive Furniture Corp. Albuquerque Boston (A) (B) Cleveland Factory (C) Capacity Des Moines (D) 5 4 3 Evansville (E) 8 4 3 Fort Lauderdale (F) 9 7 5 Warehouse Req. 300 To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 200 10 -11 200 11 100 300 700

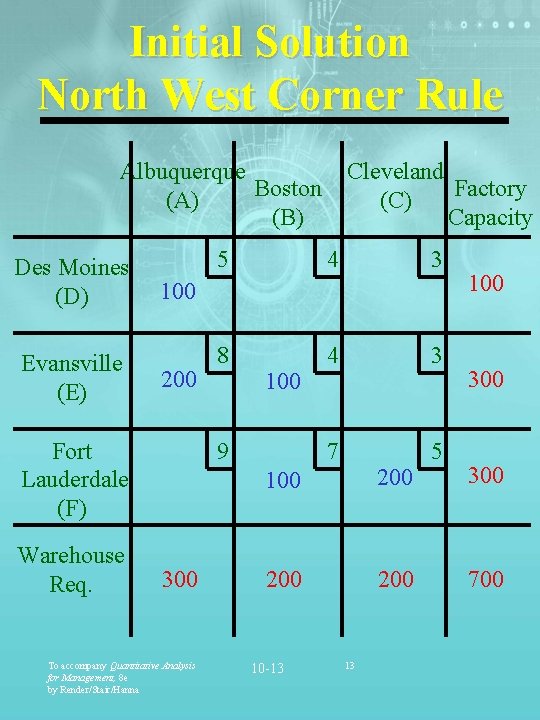
Initial Solution Using the Northwest Corner Rule • Start in the upper left-hand cell and allocate units to shipping routes as follows: • Exhaust the supply (factory capacity) of each row before moving down to the next row. • Exhaust the demand (warehouse) requirements of each column before moving to the next column to the right. • Check that all supply and demand requirements are met. To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 10 -12 12

Initial Solution North West Corner Rule Albuquerque Boston (A) (B) Des Moines (D) Evansville (E) 5 4 3 8 4 3 7 5 100 200 Fort Lauderdale (F) Warehouse Req. Cleveland Factory (C) Capacity 100 9 300 To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 100 200 200 10 -13 13 100 300 700

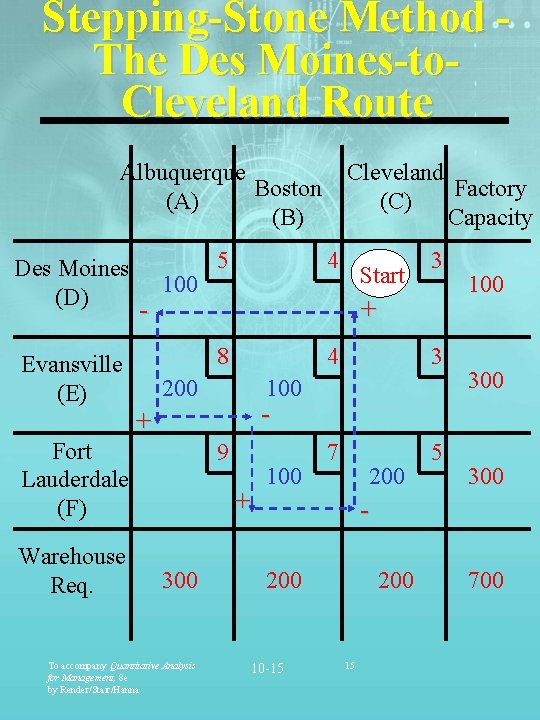
The Stepping-Stone Method • 1. Select any unused square to evaluate. • 2. Begin at this square. Trace a closed path back to the original square via squares that are currently being used (only horizontal or vertical moves allowed). • 3. Place + in unused square; alternate - and + on each corner square of the closed path. • 4. Calculate improvement index: add together the unit cost figures found in each square containing a +; subtract the unit cost figure in each square containing a -. • 5. Repeat steps 1 - 4 for each unused square. To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 10 -14 14

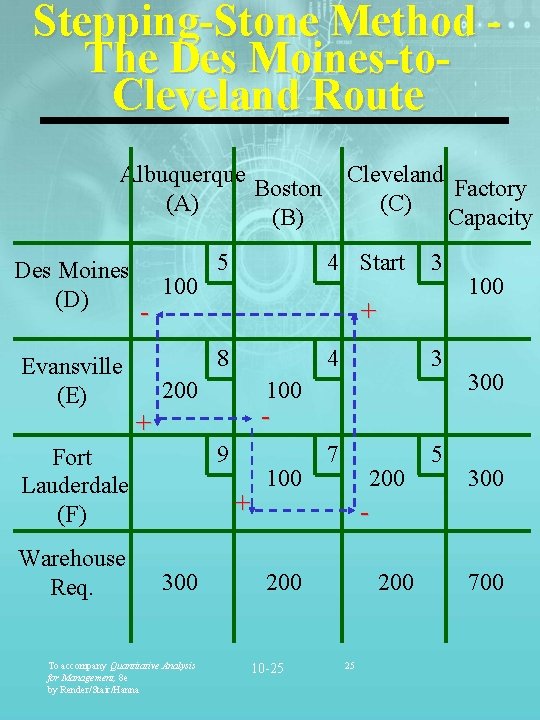
Stepping-Stone Method The Des Moines-to. Cleveland Route Albuquerque Boston (A) (B) Des Moines (D) Evansville (E) - 100 4 200 4 3 7 5 100 300 9 + To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 3 100 + 300 Start + 8 Fort Lauderdale (F) Warehouse Req. 5 Cleveland Factory (C) Capacity 100 200 300 200 10 -15 200 15 700

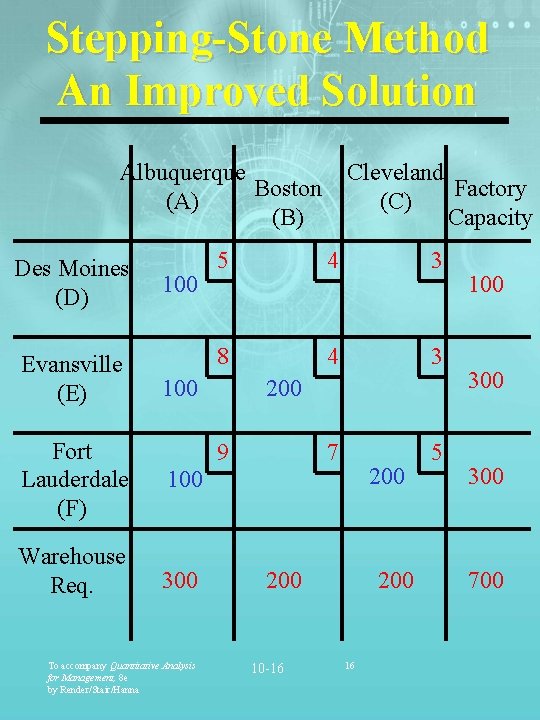
Stepping-Stone Method An Improved Solution Albuquerque Boston (A) (B) Des Moines (D) Evansville (E) 100 5 4 3 8 4 3 7 5 100 Fort Lauderdale (F) 100 Warehouse Req. 300 200 9 To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna Cleveland Factory (C) Capacity 200 10 -16 200 16 100 300 700

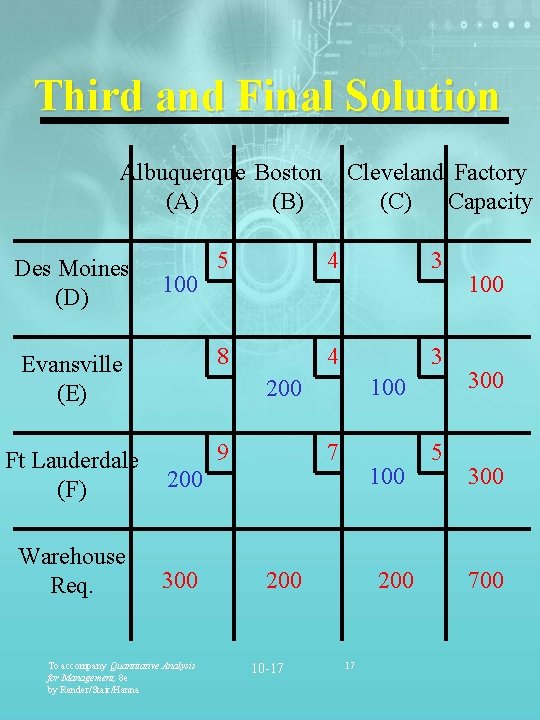
Third and Final Solution Albuquerque Boston (A) (B) Cleveland Factory (C) Capacity 5 4 3 Evansville (E) 8 4 3 Ft Lauderdale (F) 9 200 Warehouse Req. 300 Des Moines (D) 100 200 To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 7 100 200 10 -17 200 17 5 100 300 700

MODI Method: 5 Steps 1. Compute the values for each row and column: set Ri + Kj = Cij for those squares currently used or occupied. 2. After writing all equations, set R 1 = 0. 3. Solve the system of equations for Ri and Kj values. 4. Compute the improvement index for each unused square by the formula improvement index: Cij - Ri - Kj 5. Select the largest negative index and proceed to solve the problem as you did using the stepping-stone method. To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 10 -18 18

Vogel’s Approximation 1. For each row/column of table, find difference between two lowest costs. (Opportunity cost) 2. Find greatest opportunity cost. 3. Assign as many units as possible to lowest cost square in row/column with greatest opportunity cost. 4. Eliminate row or column which has been completely satisfied. 4. Begin again, omitting eliminated rows/columns. To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 10 -19 19

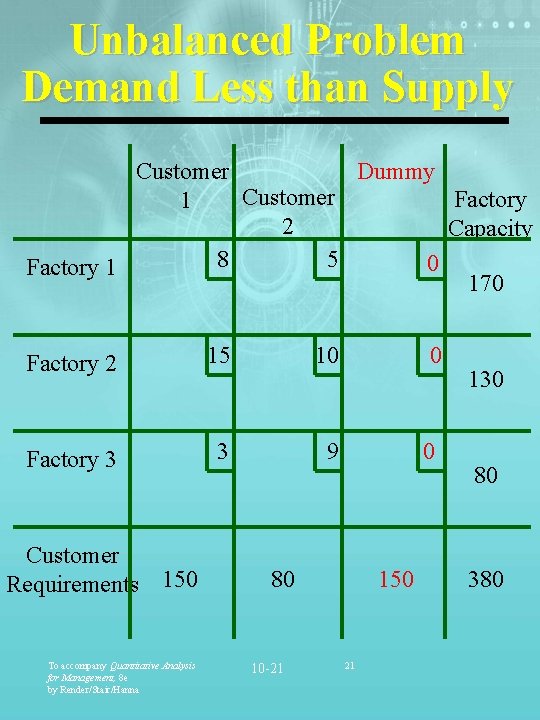
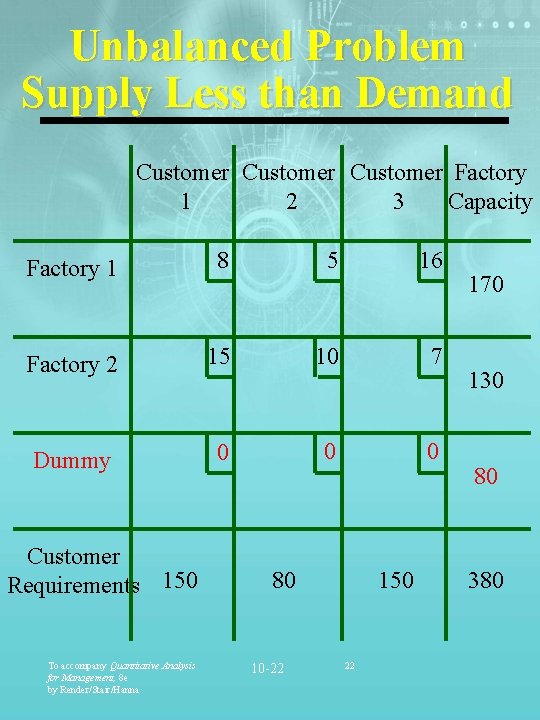
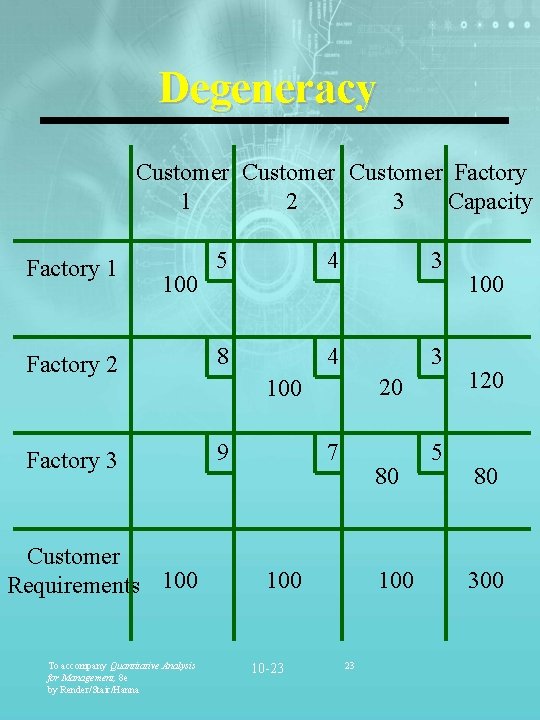
Special Problems in Transportation Method • Unbalanced Problem • Demand Less than Supply • Demand Greater than Supply • Degeneracy • More Than One Optimal Solution To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 10 -20 20

Unbalanced Problem Demand Less than Supply Customer Dummy Customer Factory 1 2 Capacity 8 5 0 Factory 1 170 Factory 2 15 10 0 Factory 3 3 9 0 Customer Requirements 150 To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 80 10 -21 150 21 130 80 380

Unbalanced Problem Supply Less than Demand Customer Factory 2 1 3 Capacity Factory 1 8 5 16 Factory 2 15 10 7 Dummy 0 0 0 Customer Requirements 150 To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 80 10 -22 150 22 170 130 80 380

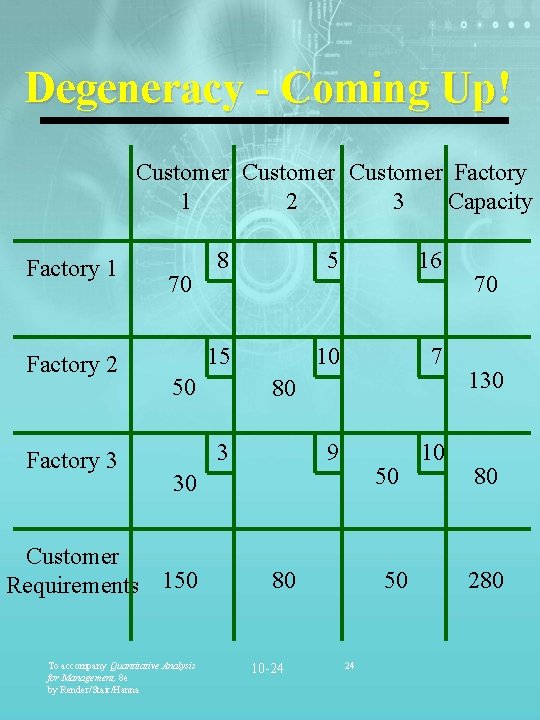
Degeneracy Customer Factory 2 1 3 Capacity 5 4 3 Factory 2 8 4 3 Factory 3 9 Factory 1 100 Customer Requirements 100 To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 20 100 7 80 10 -23 100 23 5 100 120 80 300

Degeneracy - Coming Up! Customer Factory 2 1 3 Capacity Factory 1 Factory 2 Factory 3 70 8 5 16 15 10 7 9 10 50 80 3 50 30 Customer Requirements 150 To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 80 10 -24 50 24 70 130 80 280

Stepping-Stone Method The Des Moines-to. Cleveland Route Albuquerque Boston (A) (B) Des Moines (D) Evansville (E) - 100 4 Start 200 3 7 5 100 300 9 + To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 4 100 + 300 3 + 8 Fort Lauderdale (F) Warehouse Req. 5 Cleveland Factory (C) Capacity 100 200 300 200 10 -25 200 25 700

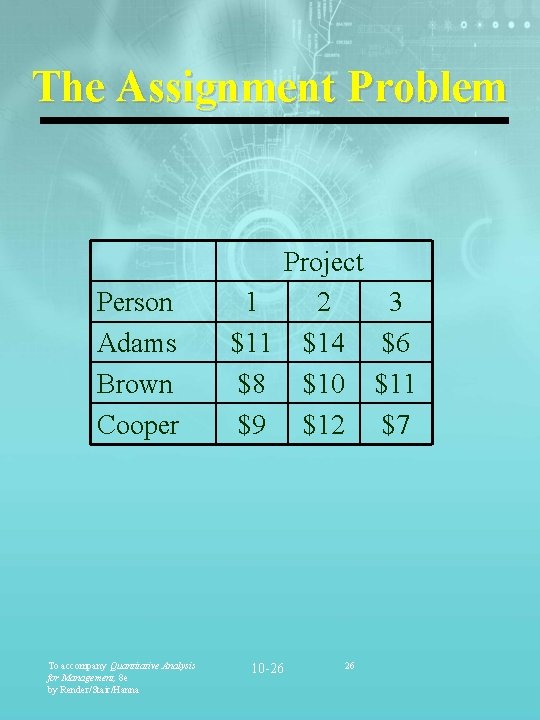
The Assignment Problem Person Adams Brown Cooper To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 1 $11 $8 $9 10 -26 Project 2 $14 $10 $12 26 3 $6 $11 $7

The Assignment Method 1. subtract the smallest number in each row from every number in that row • subtract the smallest number in each column from every number in that column 2. draw the minimum number of vertical and horizontal straight lines necessary to cover zeros in the table • if the number of lines equals the number of rows or columns, then one can make an optimal assignment (step 4) To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 10 -27 27

The Assignment Method - continued 3. if the number of lines does not equal the number of rows or columns • subtract the smallest number not covered by a line from every other uncovered number • add the same number to any number lying at the intersection of any two lines • return to step 2 4. make optimal assignments at locations of zeros within the table To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 10 -28 PG 10. 13 b 28

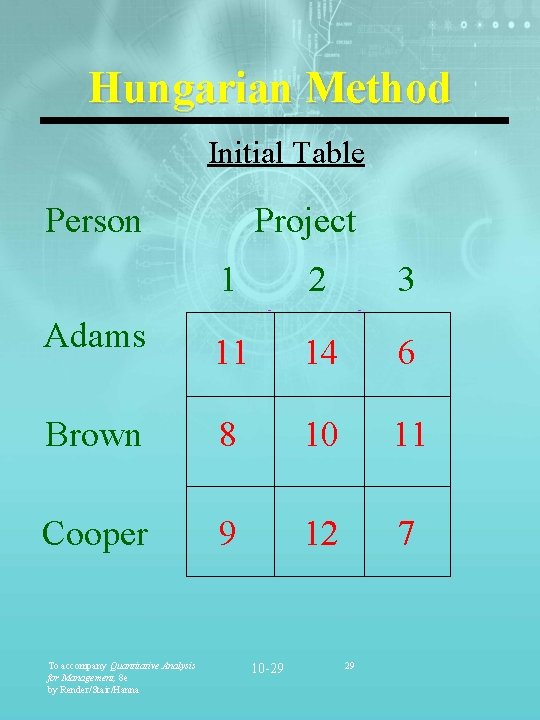
Hungarian Method Initial Table Person Project 1 2 3 Adams 11 14 6 Brown 8 10 11 Cooper 9 12 7 To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 10 -29 29

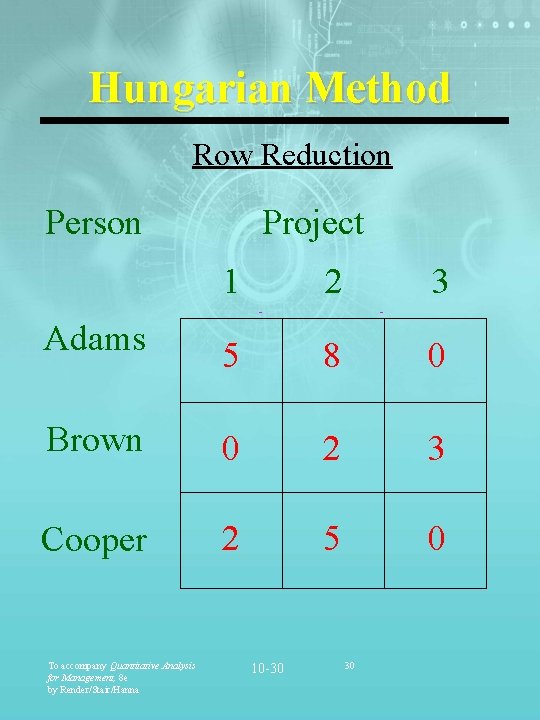
Hungarian Method Row Reduction Person Project 1 2 3 Adams 5 8 0 Brown 0 2 3 Cooper 2 5 0 To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 10 -30 30

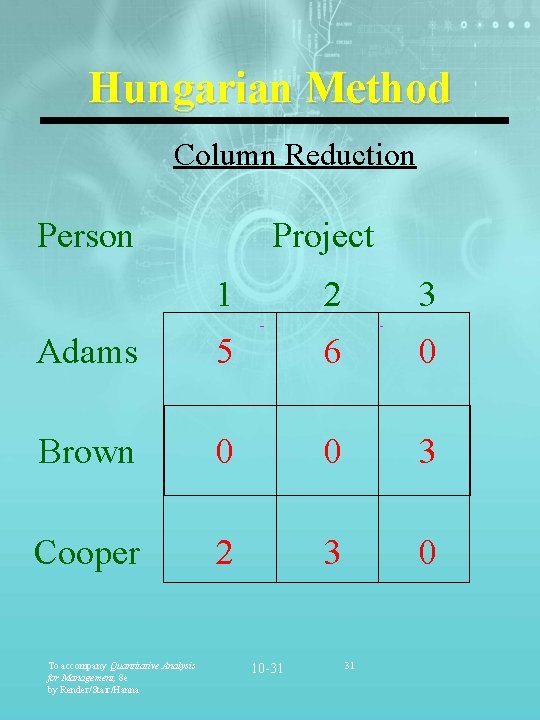
Hungarian Method Column Reduction Person Project 1 2 3 Adams 5 6 0 Brown 0 0 3 Cooper 2 3 0 To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 10 -31 31

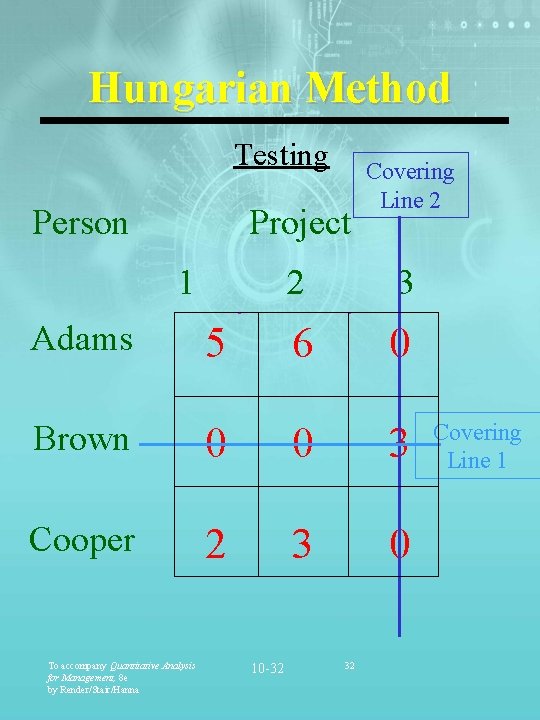
Hungarian Method Testing Person Project 1 Adams 5 Covering Line 2 2 3 6 0 Brown 0 0 3 Cooper 2 3 0 To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 10 -32 32 Covering Line 1

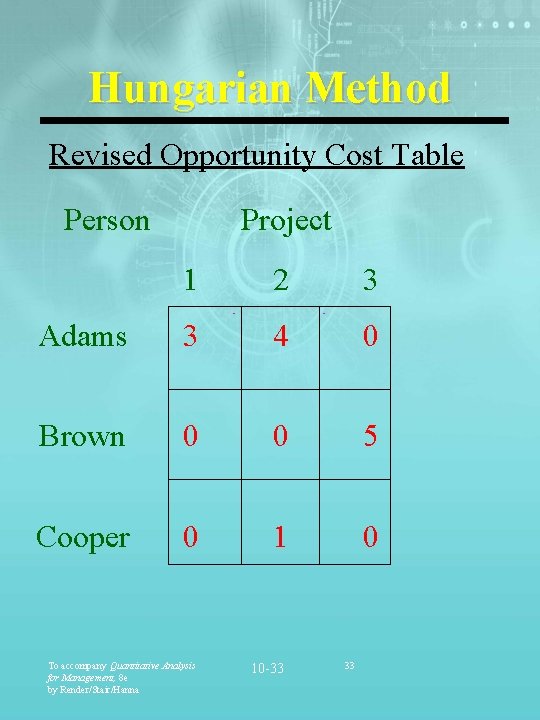
Hungarian Method Revised Opportunity Cost Table Person Project 1 2 3 Adams 3 4 0 Brown 0 0 5 Cooper 0 1 0 To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 10 -33 33

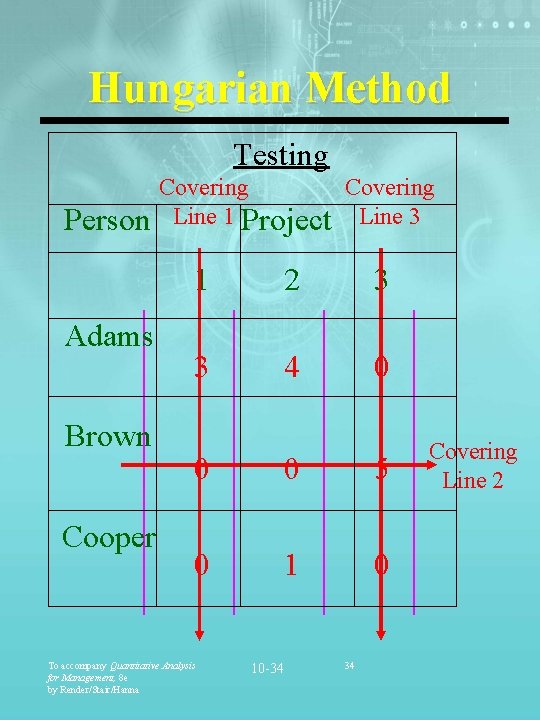
Hungarian Method Testing Person Adams Brown Cooper Covering Line 1 Project Line 3 1 2 3 3 4 0 0 0 5 0 1 0 To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 10 -34 34 Covering Line 2

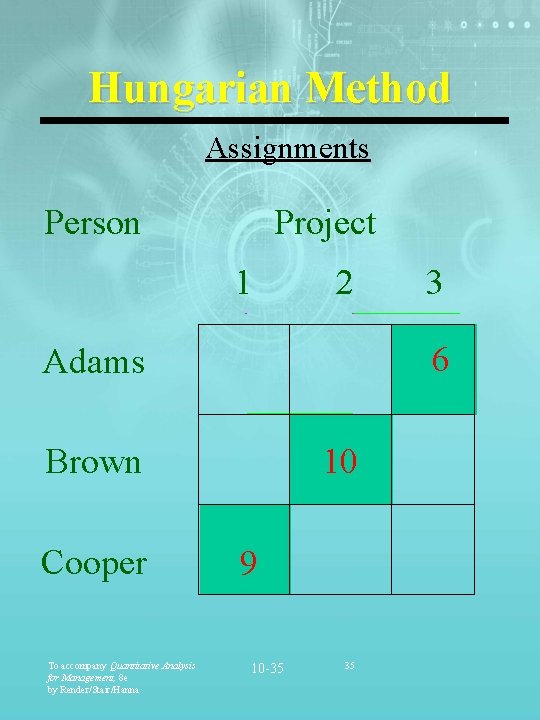
Hungarian Method Assignments Person Project 1 2 6 Adams Brown Cooper To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 3 10 9 10 -35 35

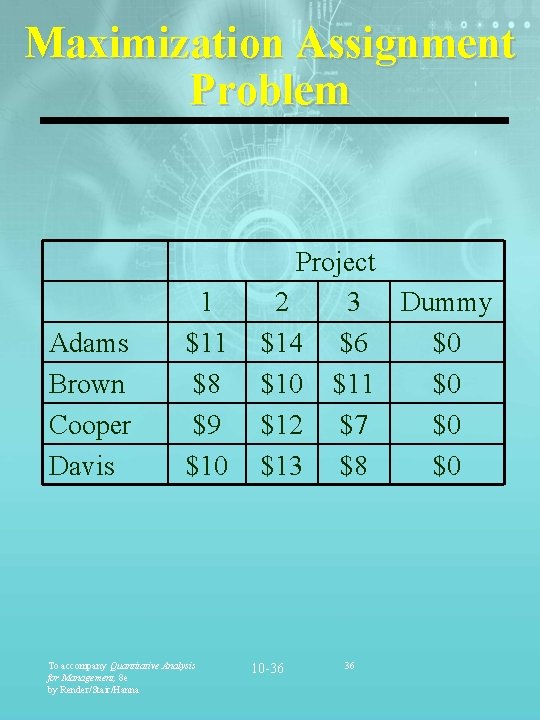
Maximization Assignment Problem Adams Brown Cooper Davis 1 $11 $8 $9 $10 To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna Project 2 3 Dummy $14 $6 $0 $11 $0 $12 $7 $0 $13 $8 $0 10 -36 36

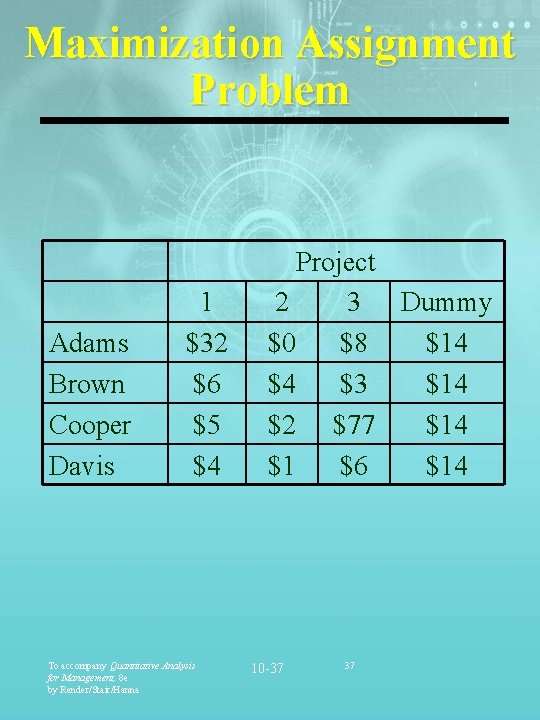
Maximization Assignment Problem Adams Brown Cooper Davis 1 $32 $6 $5 $4 To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna Project 2 3 Dummy $0 $8 $14 $4 $3 $14 $2 $77 $14 $1 $6 $14 10 -37 37