Chapter 10 Thermodynamics 10 1 Relationship Between Heat

Chapter 10: Thermodynamics

10 -1 Relationship Between Heat and Work • In a closed system there’s a direct relationship between heat and work. Heat and work both transfer energy to or from a system. • Key idea: A system never has “heat” or “work”, it has internal energy which is affected by heat in/out or work done on/by the system

Transfer of heat and work • System: a set of particles or interacting particles considered to be a distinct physical entity • Environment: the combination of conditions and influences outside a system that affects the behavior of the system • Ex of closed systems: a gas confined in a cylinder by a piston, a calorimeter, a thermos…

Work Done on or By a Gas • Is represented in the equation: W = PΔV W - in Joules (J) P = pressure in Pascal (Pa) 1 Pa = 1 N/m 2 ΔV= volume change in (m 3)

Sample Problem • Gas in a container is at a pressure of 1. 6 x 105 Pa and a volume of 4. 0 m 3. What is the work by the gas if it expands at a constant pressure to twice its initial volume?

Solution P= 1. 6 x 105 Pa =1. 6 x 105 N/m 2 ∆V=Vf – Vi = 8. 0 m 3 - 4. 0 m 3 =4. 0 m 3 W= P ∆ V W = (1. 6 x 105 N/m 2)(4. 0 m 3) W= 6. 4 x 105 J

Thermodynamic Processes • Isovolumetric process: a thermodynamic process that takes place at a constant volume so that no work is done on or by the system, ex: a car with closed windows parked in a hot garage. • Isothermal process: a thermodynamic process that takes place at a constant temperature, ex usually a slow process like a balloon expanding slowly during the day. • Adiabatic process: a thermodynamic process during which heat energy is transferred to or from the system. ex: usually a fast process like filling a tank • Isobaric process: a process that takes place at a constant pressure. ex: heating an open pot of water

10. 2 The First Law of Thermodynamics • The first law is a statement of conservation of energy that takes into account a system’s internal energy (U) as well as the energy transfer to/from the system by work and heat. • It is expressed as:

Signs of Q and W For a System ΔQ = positive if heat is added to a system ΔQ = negative if heat is released from a system ΔW = positive if work is done by the system ΔW = negative if work is done on the system

First Law – Isovolumetric Process Δ U = Q – W ΔV = 0 Since W = P ΔV, W = 0 therefore, Δ U = Q

First Law – Isothermal Process ΔU = Q – W since ΔT = 0 , ΔU = 0 therefore Q = W

First Law – Adiabatic Process Δ U = Q – W Q = 0, therefore Δ U = – W

First Law – Isobaric Process Δ U = Q – W since W = PΔV Δ U = Q – PΔV

First Law – Isolated System Δ U = Q – W since Q = W = 0 Δ U = 0

Sample Problem • A total of 135 J of work is done on a gaseous refrigerant as it undergoes compression. If the internal energy of the gas increases by 114 J during the process, what is the total amount of energy transferred as heat?

Solution W= -135 J (work done on the system is -) ∆ U= 114 J ∆ U = Q - W Q = ∆ U + W Q= 114 J + (-135 J)= -21 J Q= -21 J In this problem, energy is removed from the gas as heat, which is indicated by the negative sign on the Q value ( Q < 0 ).

Cyclic Processes • A thermodynamic process in which a system returns to the same conditions under which it started (no change in system’s energy) ΔUnet = 0 and Qnet = Wnet • Resembles an isothermal process in that all energy is transferred as work and heat.

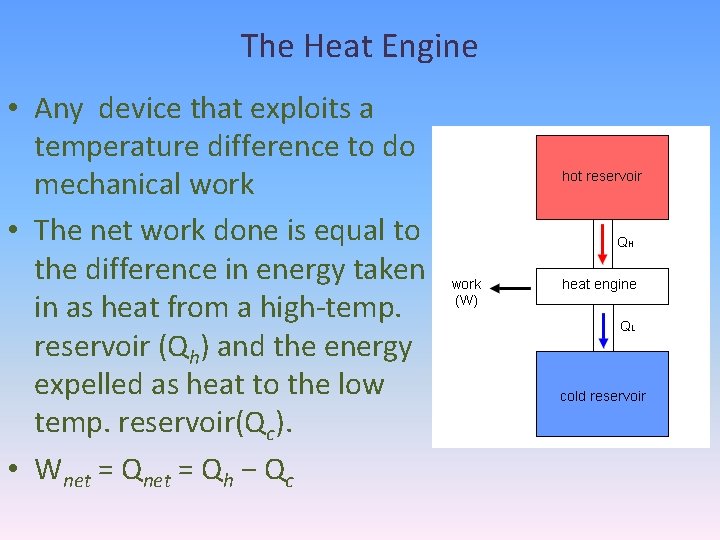
The Heat Engine • Any device that exploits a temperature difference to do mechanical work • The net work done is equal to the difference in energy taken in as heat from a high-temp. reservoir (Qh) and the energy expelled as heat to the low temp. reservoir(Qc). • Wnet = Qh − Qc

10. 3 The Second Law of Thermodynamics • States that no cyclic process that converts heat entirely into work is possible. • Includes the requirement that a heat engine give up some energy at a lower temperature in order to do work. • So a heat engine cannot transfer all energy as heat to do work.

Second Law of Thermodynamics • No cyclic process that converts heat entirely into work is possible

Efficiency of a Heat Engine • The smaller the fraction of usable energy that an engine can provide, the lower its efficiency is.

Sample Problem • Find the efficiency of a gasoline engine that, during one cycle, receives 204 J of energy from combustion and loses 153 J as heat into the exhaust.

Solution Qh= 204 J Qc= 153 J eff= 1 - Qc Qh eff= 1 - 153 J 204 J eff= 0. 250 J

Entropy • Entropy: a measure of the randomness or disorder of a system • A greater disorder means there is less energy to do work • The motion of the particles of a system is not well ordered and therefore is less useful for doing work

• Once a system has reached a state of the greatest disorder, it will tend to remain in that state and have maximum entropy. • The second law of thermodynamics states that the entropy of the universe increases in all natural processes.