Chapter 10 The Three Common States of Matter


























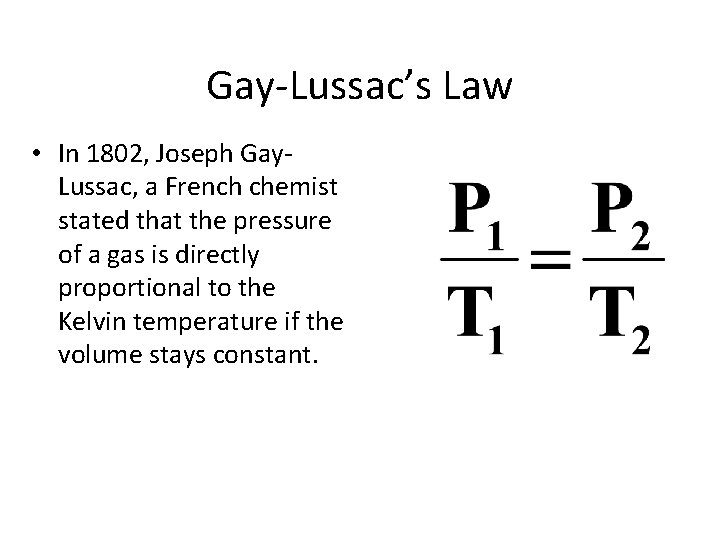

















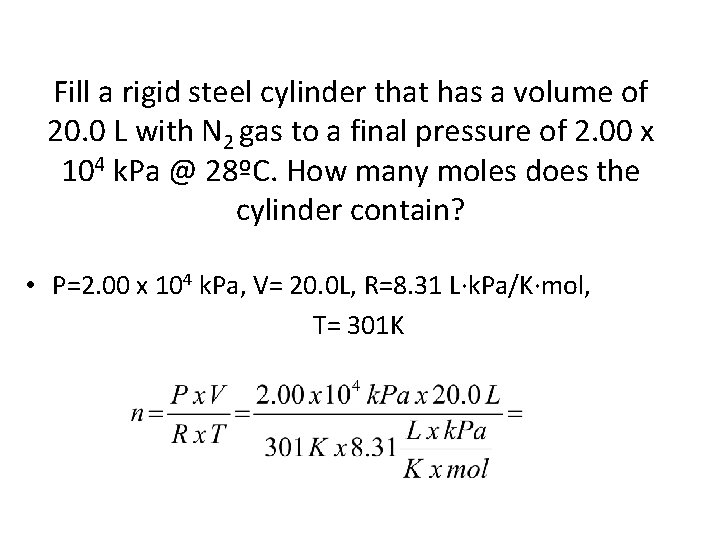







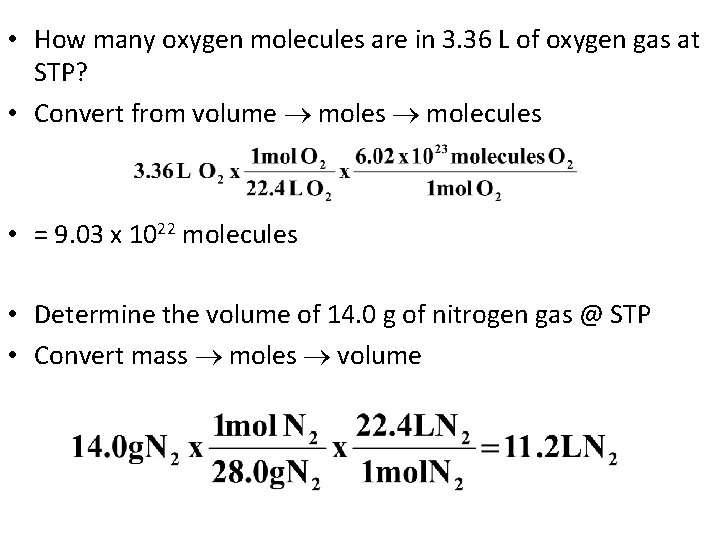





- Slides: 61

Chapter 10

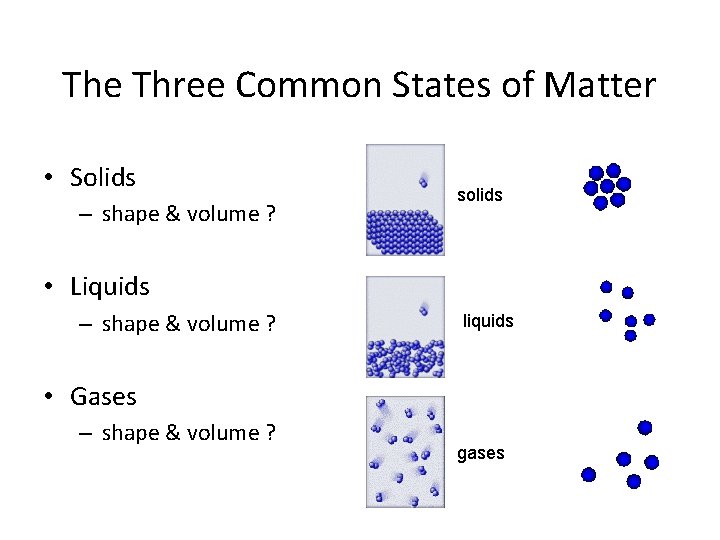
The Three Common States of Matter • Solids – shape & volume ? solids • Liquids – shape & volume ? liquids • Gases – shape & volume ? gases

Kinetic Theory - Gases • Kinetic Theory- matter is made of tiny particles that are in constant motion (Kinetic energy) • Gas is composed of molecules or atoms that are considered to be small, hard spheres that have insignificant volume. • Gas particles are far apart, and have no attractive or repulsive forces between them.

Kinetic Theory - Gases • Gas particles move rapidly in constant random motion in straight paths independent of each other. – O 2 molecules in air travel 1700 km/hr (> 500 mph) • Gases fill their containers and diffuse into space without limit.

Kinetic Theory - Gases • Gas particles move extremely fast until they strike another particle or side of the container • Collisions are perfectly elastic meaning that during a collision, kinetic energy is transferred without loss so kinetic energy stays constant

Gas Pressure • Why does the water stay in the cup? • Gas Pressure – The force exerted by a gas per unit surface area of an object • Atmospheric pressure results from collisions of air molecules with objects. It is based on the mass of one square inch of air reaching to the top of the atmosphere (75 miles!!) The weight is 14. 7 pounds. The pressure is 14. 7 PSI (pounds per sq. inch)

Barometers and Air Pressure • Older barometers measured the height of mercury in a tube which depended on the pressure created by collisions of air molecules with the surface of Hg. • At sea level, the pressure supports a column of Hg at 760 mm high. So 1 atmosphere = 760 mm Hg = 101. 3 k. Pa = 14. 7 PSI

Measuring Pressure • Si unit of pressure is pascal (Pa). • Atmospheric pressure at sea level is ~101. 3 kilopascals (k. Pa) • Other units are millimeters of mercury • ( 760 mm Hg) and atmospheres ( 1 atm) STP = OºC and 101. 3 k. Pa

Kinetic Energy and Kelvin Temperature • When a substance is heated, the average kinetic energy of the substance increases (there is a wide range of speeds that molecules are moving so we use average kinetic energy). • Temperature is the measurement of the average kinetic energy of a substance • Kelvin scale reflects relationship between temperature and average kinetic energy • Absolute zero is the temperature where all particles cease movement

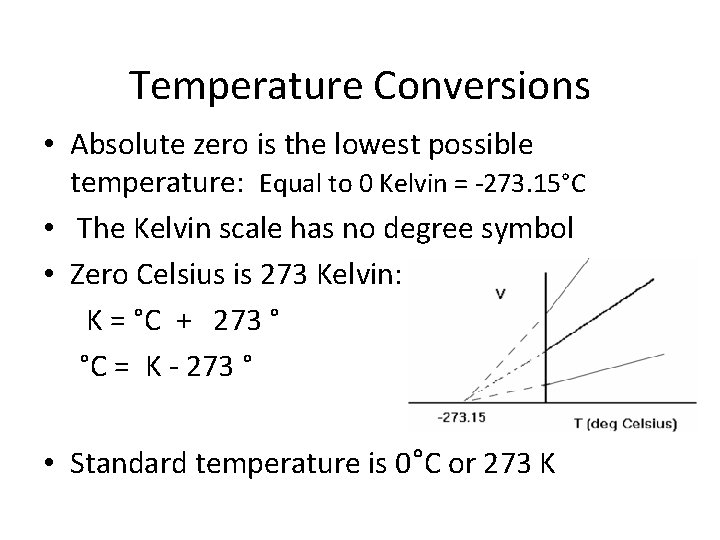
Temperature Conversions • Absolute zero is the lowest possible temperature: Equal to 0 Kelvin = -273. 15°C • The Kelvin scale has no degree symbol • Zero Celsius is 273 Kelvin: K = °C + 273 ° °C = K - 273 ° • Standard temperature is 0°C or 273 K

3 Properties of Gases 1. Compressibility is measure of how much the volume of matter decreases with increased pressure. Gases are easily compressed because of the space between molecules 2. No attractive or repulsive forces exist between atoms or molecules 3. Gas particles move rapidly in constant random motion in straight paths independently of each other

4 Variables That Describe a Gas 1. 2. 3. 4. • Pressure- (P) in kilopascals Volume- (V) in liters Temperature- (T) in Kelvins Number of moles- (n) Gas laws will enable you to predict gas behavior at specific conditions

Factors Affecting Gas Pressure Amount, Volume, and Temperature

Amount of Gas • Increasing the number of particles increases the number of collisions so the pressure increases (↑) • Keeping the temperature constant, doubling the number of particles doubles the pressure • When a sealed container of gas under pressure is opened, the gas moves from the region of higher pressure to the region of lower pressure

Volume • Pressure can be raised by reducing the volume of the gas • The more the gas is compressed, the greater the pressure it exerts inside the container • Reducing volume by half doubles the pressure • Increasing the volume has the opposite effect of decreasing the pressure • Doubling the volume halves the pressure

Temperature • Speed and kinetic energy of gas particles increase as particles absorb thermal energy • Faster moving particles impact the walls of their container with more energy, exerting more pressure • If average kinetic energy of gas doubles, the Kelvin temperature doubles, and pressure of the enclosed gas also doubles

Boyle The Gas Laws Boyle’s, Charles’, Gay-Lussac’s, and the Combined Gas Laws Charles

Pressure-Volume Relationship Boyle’s Law • For a given mass of gas at constant temperature, the volume of the gas varies inversely with pressure • If volume goes , pressure goes • If pressure goes , volume goes • The product of pressure and volume at any 2 sets of conditions at given temp is constant so…… P 1 x V 1 = P 2 x V 2

A high altitude balloon contains 30. 0 L of He gas at 103 k. Pa. What is the volume when balloon increases altitude to when pressure is 25. 0 k. Pa? • P 1 x V 1 = P 2 x V 2 – P 1 = 103 k. Pa – P 2 = 25. 0 k. Pa – V 1 = 30. 0 L • V 2 = ?

• 103 k. Pa x 30. 0 L = V 2 x 25. 0 k. Pa • V 2 = 124 L • Does this make sense? Yes, a decrease in pressure at constant temperature corresponds to a proportional increase in volume.

• The pressure on 2. 50 L of anesthetic gas changes from 105 k. Pa to 40. 5 k. Pa. What will be the new volume if the temperature remains constant? • What is the unknown? • What will happen to the size of the unknown? • Answer: (2. 5 L) (105 k. Pa) = (? L) (40. 5 k. Pa) ? = 6. 5 L

• A gas with a volume of 4. 0 L at a pressure of 205 k. Pa is allowed to expand to a volume of 12. 0 L. What is the pressure in the container if the temperature remains constant? • What will happen to the pressure as volume increases? • Answer: (4. 0 L) (205 k. Pa) = (12. 0 L) (? k. Pa) ? = 68. 3 k. Pa

Temperature -Volume Relationship Charles’ Law

Charles’s Law • 1 n 1787, French physicist and balloonist Jacques Charles investigated the effect of temperature on volume of a gas at constant pressure • Found increase in volume with every increase in temperature that he studied

Graph of Temperature-Volume Relationship • T vs. V yields a straight line graph • Graphs of all gas samples, when extrapolated to a volume of zero, intersect at the same point, -273. 15 ºC (Why? ) • William Thomson (Lord Kelvin) realized the importance of this number and identified it as absolute zero where theoretically the average kinetic energy of gas particles is zero

Charles’s Law • Volume of a fixed mass of gas is directly proportional to its Kelvin temperature if the pressure is constant

A balloon inflated @ 24 ºC has a volume of 4. 00 L. The balloon is heated to 61ºC. What is the new volume if the pressure remains constant? • V 1 = 4. 00 L T 1 = 24ºC T 2 = 61 ºC V 2 = ? • V 2 = 4. 5 L • Does this make sense? Yes, from kinetic theory the volume should increase with increase in temperature at constant pressure.

Sample Problems • If a gas occupies 6. 80 L at 325ºC, what is the volume at 25 ºC if no change in pressure? Will the volume go up or down? • Answer: • 5. 00 L of air at – 50. 0 ºC is warmed to 100. 0 ºC. What is new volume @ constant pressure? What direction will the volume move? • Answer:

Temperature-Pressure Relationship Gay-Lussac’s Law
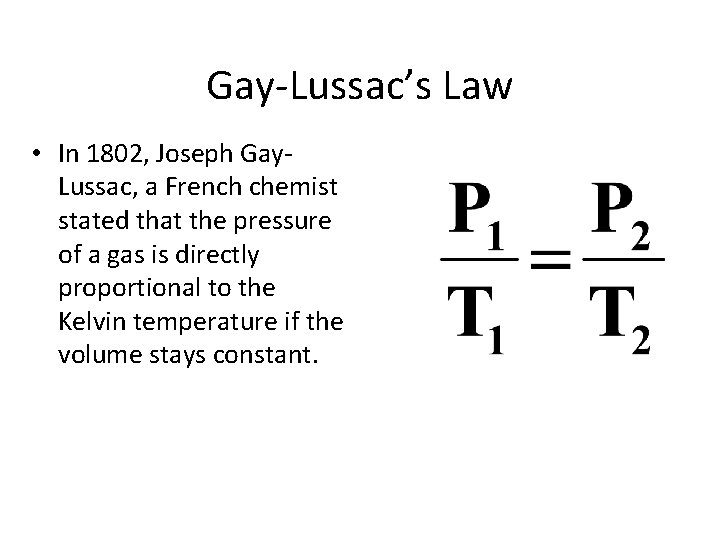
Gay-Lussac’s Law • In 1802, Joseph Gay. Lussac, a French chemist stated that the pressure of a gas is directly proportional to the Kelvin temperature if the volume stays constant.

• Gas left in a used aerosol can is at a pressure of 103 k. Pa @ 25ºC. If thrown into a fire, what is the pressure at 928 ºC? • P 1 = 103 k. Pa T 1 = 25 ºC T 2 = 928 ºC P 2 =? • Remember temperature must be in Kelvin!

• A gas has a pressure of 6. 58 k. Pa at 539 K. What will be pressure @ 211 K given constant volume? • Pressure in an automobile tire is 198 k. Pa @ 27 ºC. At the end of the trip, the pressure has risen to 225 k. Pa. What is the temperature of the air in the tire?

So you think you’ve had a bad day?

The Combined Gas Law Combines the 3 gas laws o. Holding one value constant, you can obtain the other gas laws o. Can be used when none of the variables are constant

Volume of a gas-filled balloon is 30. 0 L @ 40 ºC and 153 k. Pa. What volume will the balloon have at STP? – – – • V 1 = 30. 0 L T 1 = 40 ºC T 2 = 273 K P 1 = 153 k. Pa P 2 = 101. 3 k. Pa V 2 = ?

V 2 = 39. 5 L temperature ratio is 1 ( 273 K/313 K) volume decreases pressure ratio is 1 (153 k. Pa/ 101. 3 k. Pa) volume increases When both effects are combined, volume increases

Dalton’s Law • Particles in a mixtures of gases (ex: Air) are at the same temperature so they have the same average kinetic energy • Gas pressure depends only on # of particles in a given volume and their average kinetic energy • If you know the pressure exerted by each gas in the mixture, the pressures can be added to find the total gas pressure.

Partial Pressure • One form of Dalton’s law of partial pressures: • Ptotal = P 1 + P 2 + P 3 + P 4……. . @ constant volume and temperature • Fractional contribution to pressure by each gas in a mixture does not change with changes in temperature, volume or pressure • This is very important in the area of anesthesiology.

Sample Problem • Air contains O 2, N 2, CO 2, and trace amounts of other gases. What is the partial pressure of oxygen PO 2 at 101. 30 k. Pa of total pressure if the partial pressures of nitrogen, carbon dioxide and other gases are 79. 10 k. Pa, 0. 040 k. Pa, and 0. 94 k. Pa • Ptotal = P 02 + (PN 2+PCO 2 + Pothers) • PO 2 = 21. 22 k. Pa

Sample Problems • Determine the total pressure of a gas mixture that contains O 2, N 2, and He if the partial pressures of the gases are as follows: PO 2=20. 0 k. Pa, PN 2=46. 7 k. Pa, PHe = 26. 7 k. Pa. • Answer: • A gas mixture containing O 2, N 2, and CO 2 has a total pressure of 32. 9 k. Pa. If PO 2 = 6. 6 k. Pa and PN 2 = 23. 0 k. Pa, what is PCO 2? • Answer:

End of Chapter 10

Chapter 11 Molecular Composition of Gas Ideal Gas Laws

Avogadro’s Hypothesis • Equal volumes of gases, at the same temperature and pressure contain equal numbers of particles • This is possible because there is so much space between the particles that it doesn’t matter how large or small the particles are • So 1 mole of any gas occupies 22. 4 Liters at STP conditions

Sample Problem • Determine the volume in L occupied by 0. 202 mol of a gas at STP • Does this make sense? Yes, because 1 mol of gas occupies 22. 4 L at STP so 0. 202 mol of gas would occupy about 1/5 of that volume

4 th Variable – Moles! • Amount of gas in system affects pressure and volume of gas at constant temperature. • volume or pressure depends on the # of gas particles – Moles! • Moles are expressed as “n”. • Divide each side of the combined gas equation by n

• (P x V)/(T x n) is a constant for ideal gases • If you evaluate (P x V)/(T x n) , # of moles of gas at any specified P, V, and T can be calculated - symbolized by R, the ideal gas constant • Since 1 mol of gas occupies 22. 4 L @STP, substitute #’s in to calculate R

Ideal Gas Law • Rearranging the equation, you get: • P x V = n x R x T or PV = n. RT • This allows you to solve for the # of moles when P, V, and T are known
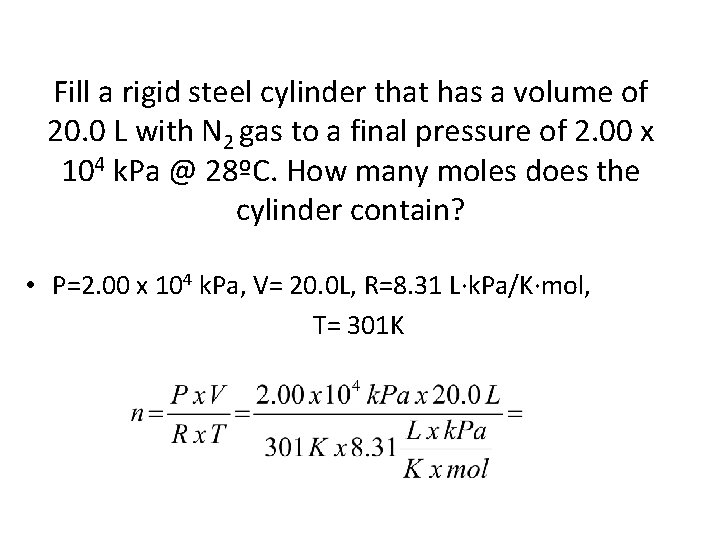
Fill a rigid steel cylinder that has a volume of 20. 0 L with N 2 gas to a final pressure of 2. 00 x 104 k. Pa @ 28ºC. How many moles does the cylinder contain? • P=2. 00 x 104 k. Pa, V= 20. 0 L, R=8. 31 L∙k. Pa/K∙mol, T= 301 K

A deep underground cavern contains 2. 24 x 106 L of CH 4(g) at a pressure of 1. 50 x 103 k. Pa and temperature of 42ºC. How many kilograms of CH 4 does this natural-gas deposit contain? • P = 1. 50 x 103 k. Pa V = 2. 24 x 106 L • Mass = ? T = 42ºC

• Convert moles of methane to grams • Convert to kilograms = 2. 05 x 104 kg CH 4 • Does this make sense? Yes, volume and pressure are very large so should be large mass of methane

Sample Problems • A child has a lung capacity of 2. 20 L. How many grams of air do her lungs hold at a pressure of 102 k. Pa and a normal body temperature of 37ºC? (Molar mass of air ~29 g/mol) • Answer: • What volume will 12. 0 g of oxygen gas occupy at 25ºC and a pressure of 52. 7 k. Pa? • Answer:

Ideal Gas Law and Kinetic Theory • Ideal gas is one that follows the gas laws at all conditions of pressure and temperature • Assumes gas conforms precisely to the kinetic theory – Particles have no volume and could not be attracted to each other at all. – There are no ideal gases but at high temperature and low pressure, real gases behave much like ideal.

Real Gases – Non Ideal • Important difference is that real gases can be liquefied and sometimes solidified by cooling and applying pressure where ideal gases cannot. • Gases become more “non ideal” at low temperatures and high pressures - Why? Gas molecules are more likely to stick together in these conditions.

Departures from Ideal Gas Law • Deviations from ideal are based on 2 factors, attractions between molecules and volume of the gas molecules • Gases could not be liquefied if there was no attraction between molecules • Actual gases are made of actual particles that have volume

• Liquid O 2 - occurs at -183 ºC • Liquid N 2 - occurs at - 196 ºC • Coldest recorded temperature on Earth Vostok, Antartica – 1983 - 89 ºC (-129 ºF)
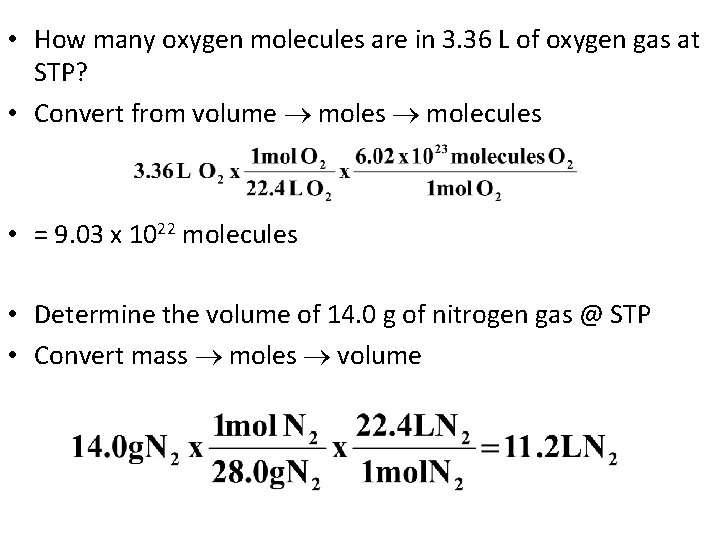
• How many oxygen molecules are in 3. 36 L of oxygen gas at STP? • Convert from volume moles molecules • = 9. 03 x 1022 molecules • Determine the volume of 14. 0 g of nitrogen gas @ STP • Convert mass moles volume

• What volume is occupied by 4. 02 x 1022 molecules of helium gas @STP? • Answer: • What is the volume of a container that holds 8. 80 g of carbon dioxide @STP? • Answer: • A container holds 6. 92 g of hydrogen gas @STP. What is the volume of the container? • Answer:

Graham’s Law • Diffusion is the tendency of molecules to move toward areas of lower concentration until the concentration is uniform throughout • Effusion is the process where a gas escapes through a tiny hole in its container • Thomas Graham (in 1840’s) studies effusion • Proposed that the rate of effusion is inversely proportional to the square root of its molar mass

• KE = ½mv 2 so…. If 2 bodies of different masses have the same kinetic energy, the lighter body must move faster • Particles at the same temperature have the same kinetic energy so the particles with lower molar mass must move faster • The rates of effusion are inversely proportional to the square roots of their molar masses

Sample Problem • Compare rates of effusion of the air component nitrogen (molar mass = 28. 0 g) and helium gas (molar mass = 4. 0 g)

Behavior of Gases