Chapter 10 Systems of Nonlinear FirstOrder Differential Equations


- Slides: 41

Chapter 10 Systems of Nonlinear First-Order Differential Equations Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018

Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 2

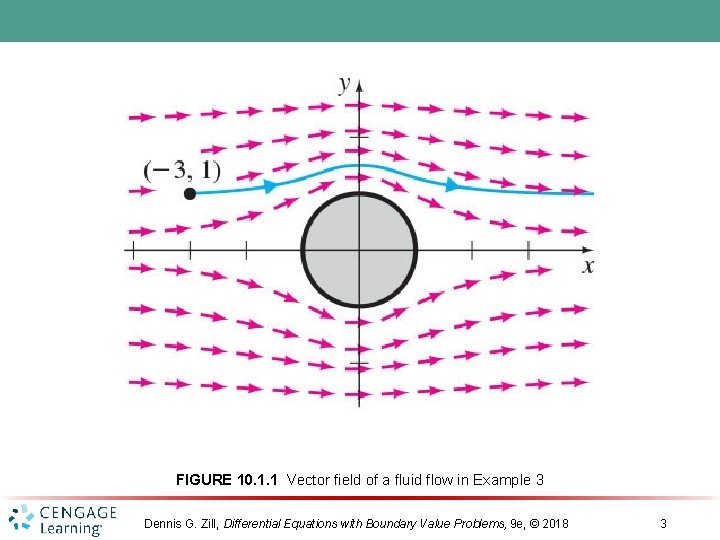
FIGURE 10. 1. 1 Vector field of a fluid flow in Example 3 Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 3

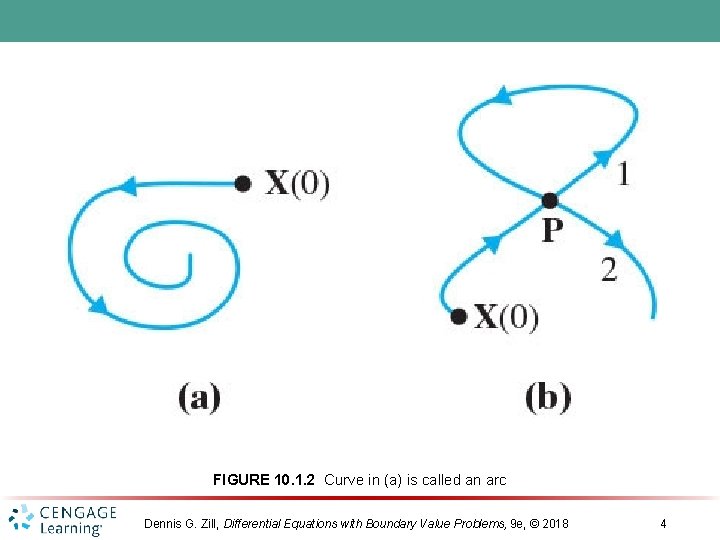
FIGURE 10. 1. 2 Curve in (a) is called an arc Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 4

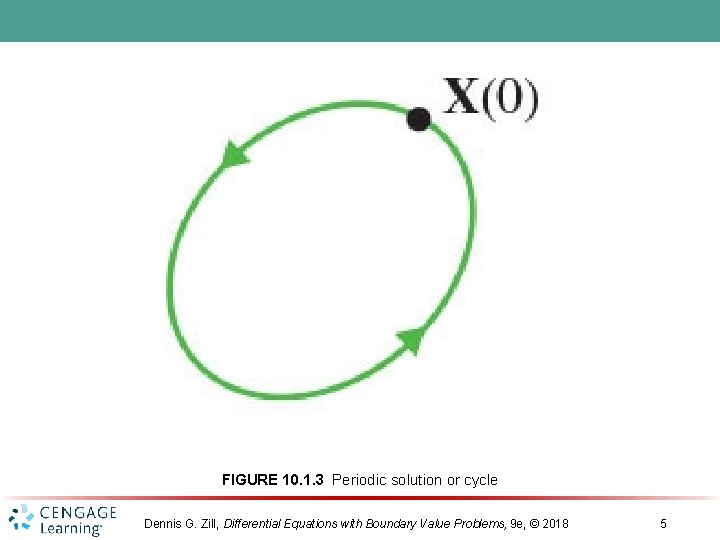
FIGURE 10. 1. 3 Periodic solution or cycle Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 5

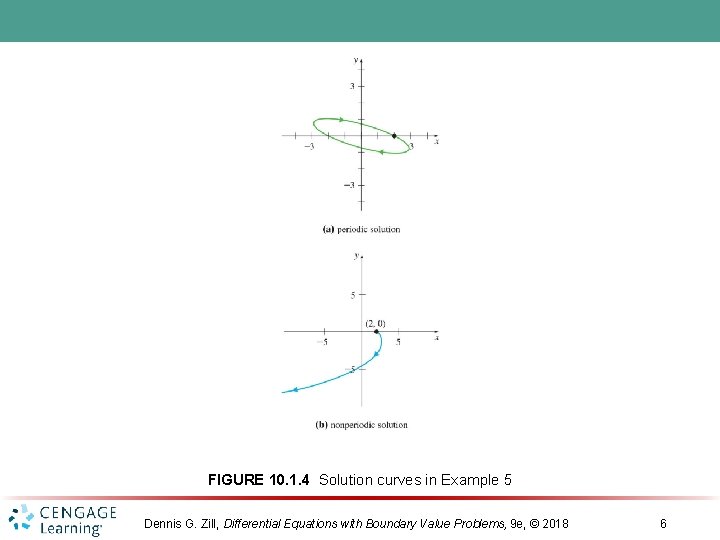
FIGURE 10. 1. 4 Solution curves in Example 5 Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 6

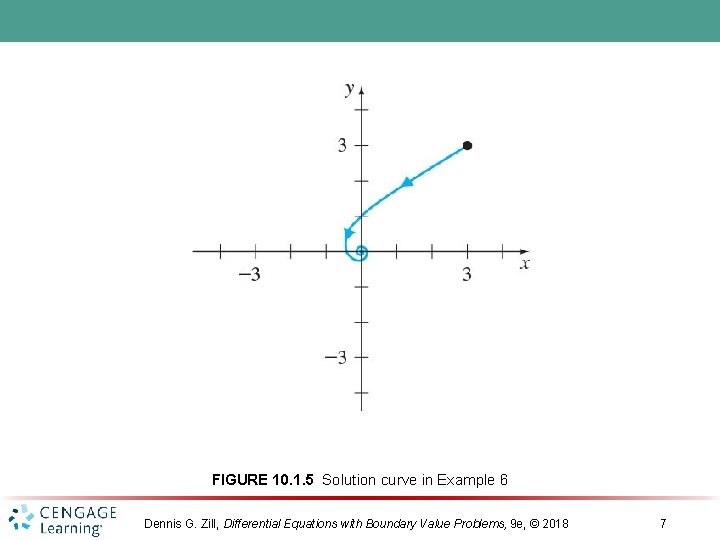
FIGURE 10. 1. 5 Solution curve in Example 6 Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 7

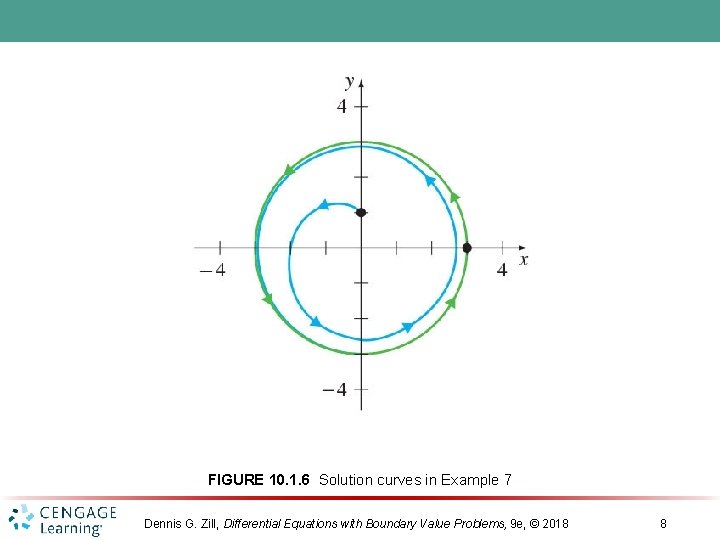
FIGURE 10. 1. 6 Solution curves in Example 7 Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 8

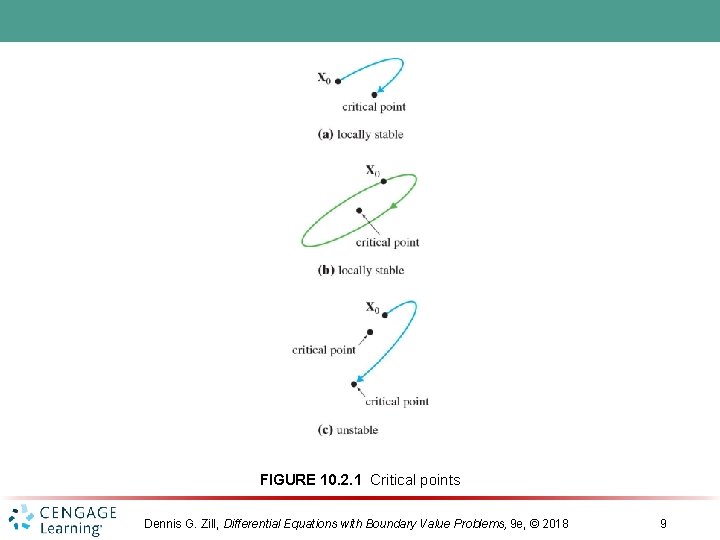
FIGURE 10. 2. 1 Critical points Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 9

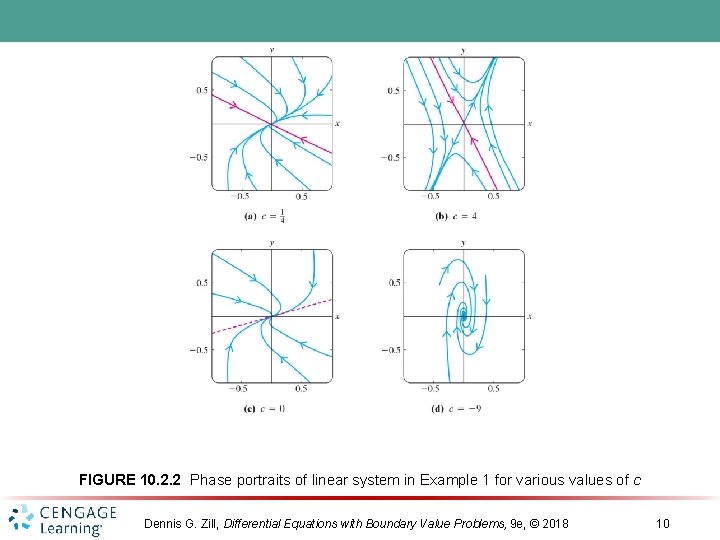
FIGURE 10. 2. 2 Phase portraits of linear system in Example 1 for various values of c Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 10

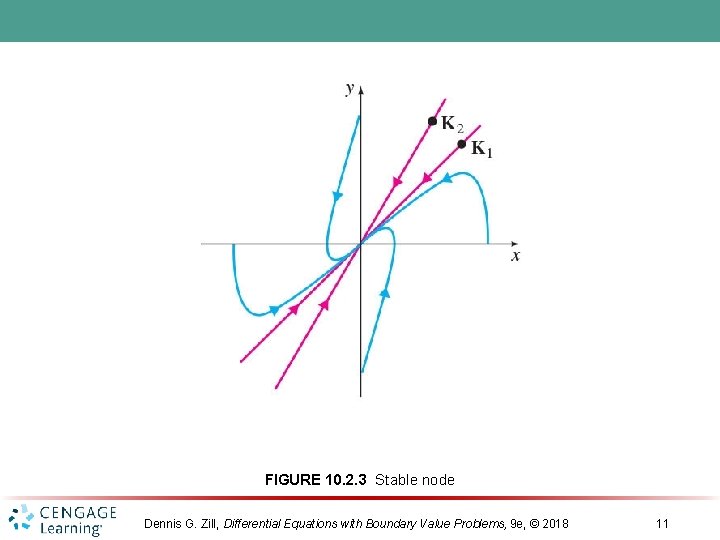
FIGURE 10. 2. 3 Stable node Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 11

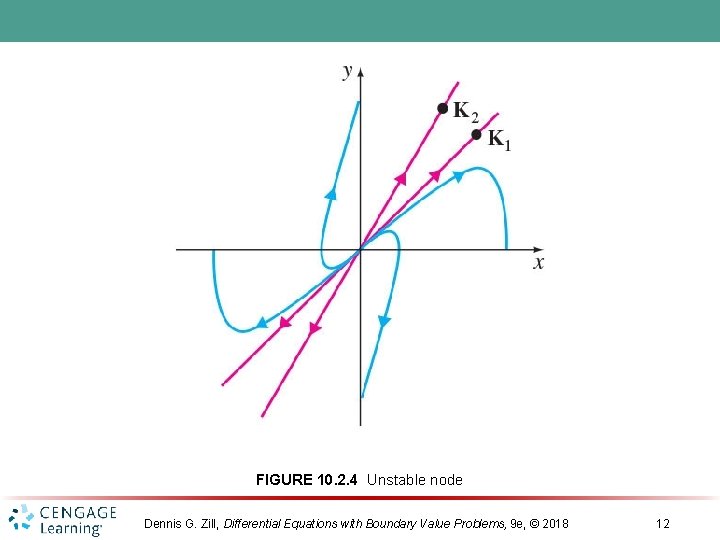
FIGURE 10. 2. 4 Unstable node Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 12

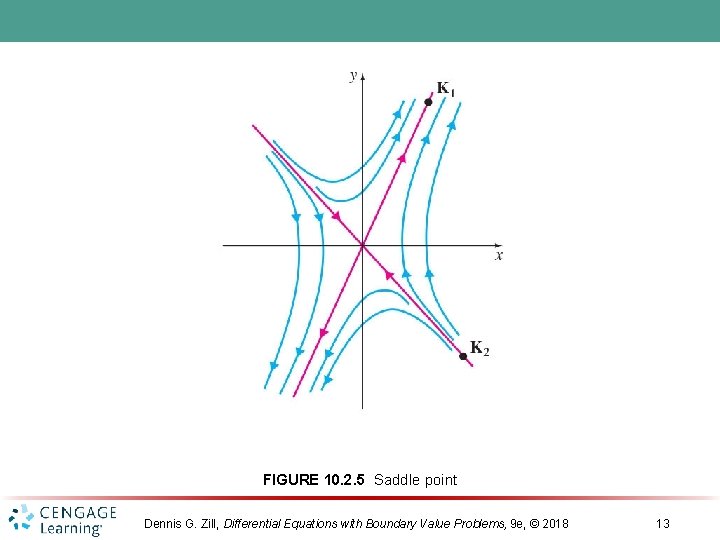
FIGURE 10. 2. 5 Saddle point Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 13

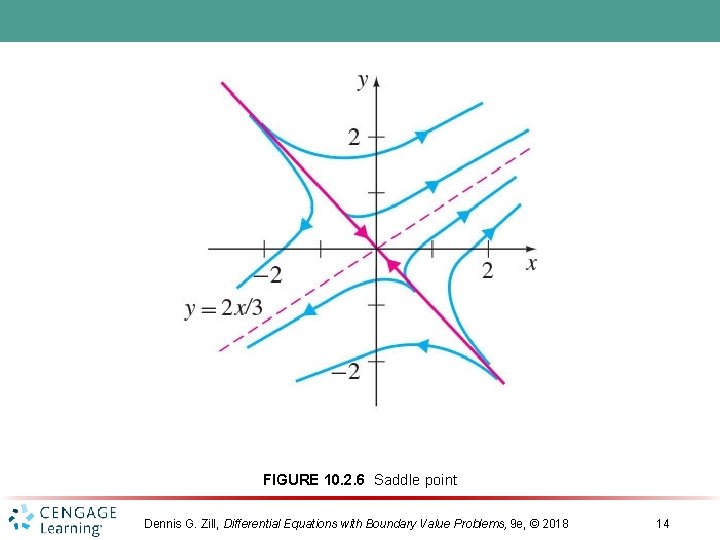
FIGURE 10. 2. 6 Saddle point Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 14

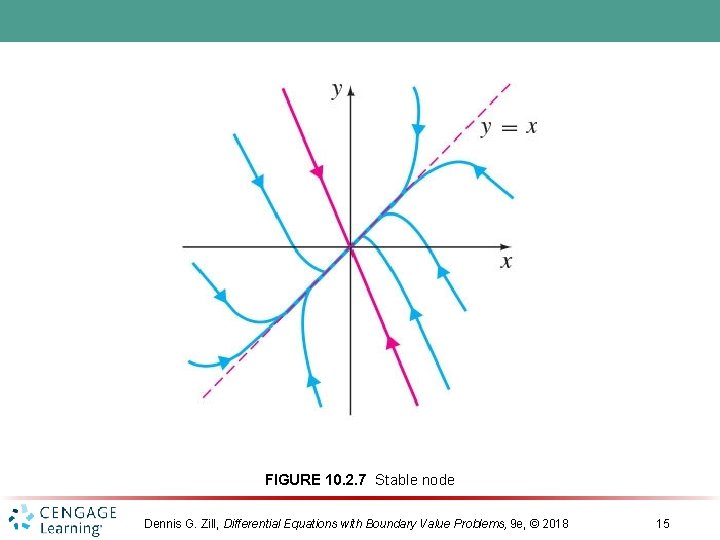
FIGURE 10. 2. 7 Stable node Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 15

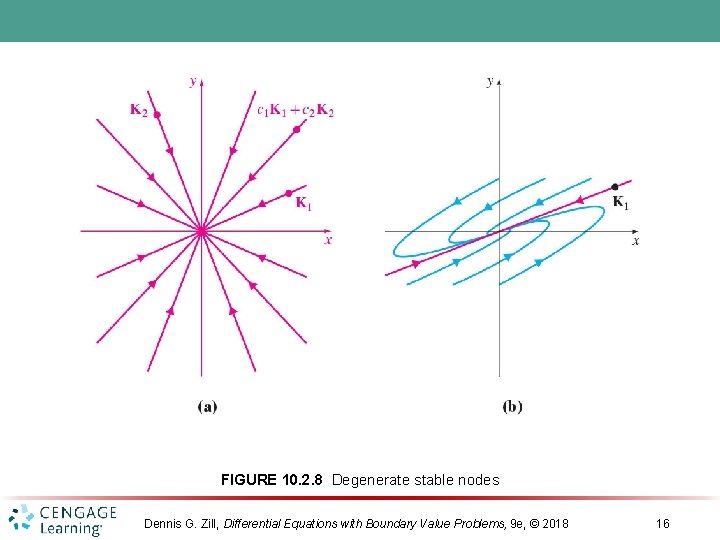
FIGURE 10. 2. 8 Degenerate stable nodes Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 16

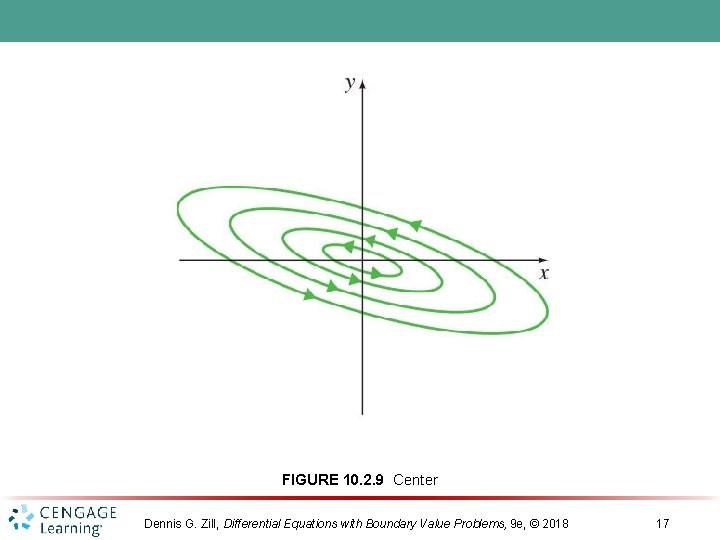
FIGURE 10. 2. 9 Center Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 17

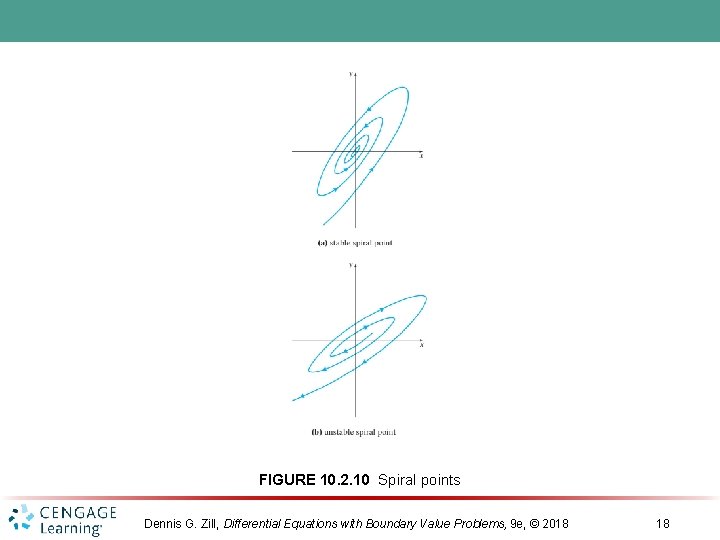
FIGURE 10. 2. 10 Spiral points Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 18

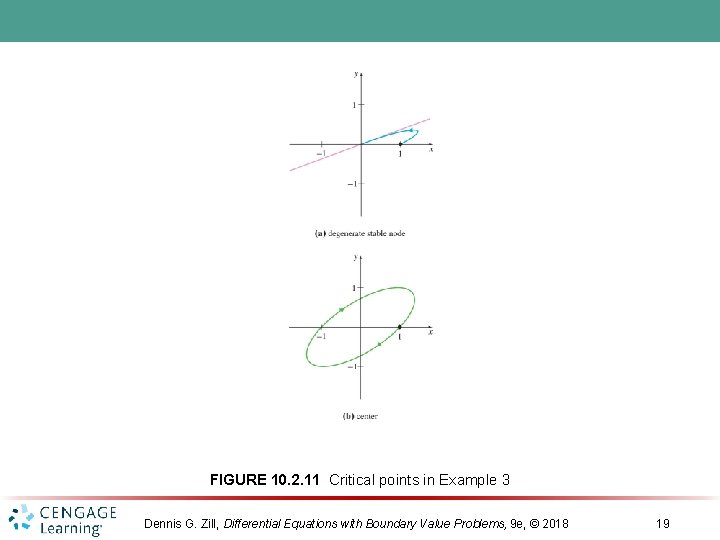
FIGURE 10. 2. 11 Critical points in Example 3 Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 19

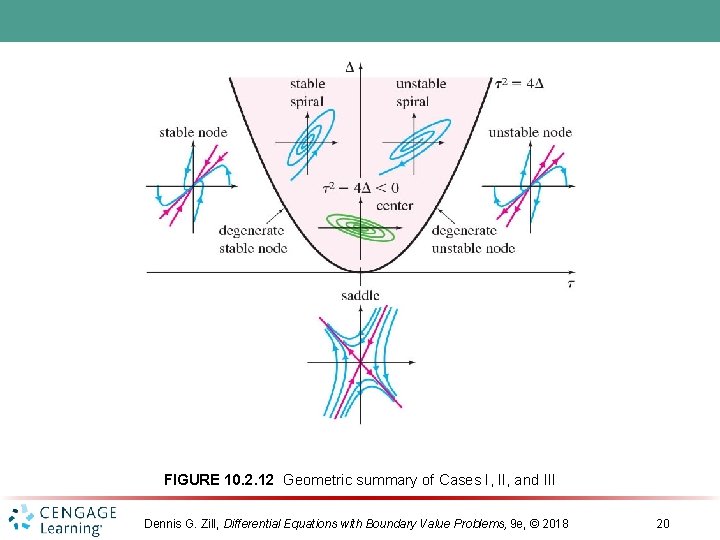
FIGURE 10. 2. 12 Geometric summary of Cases I, II, and III Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 20

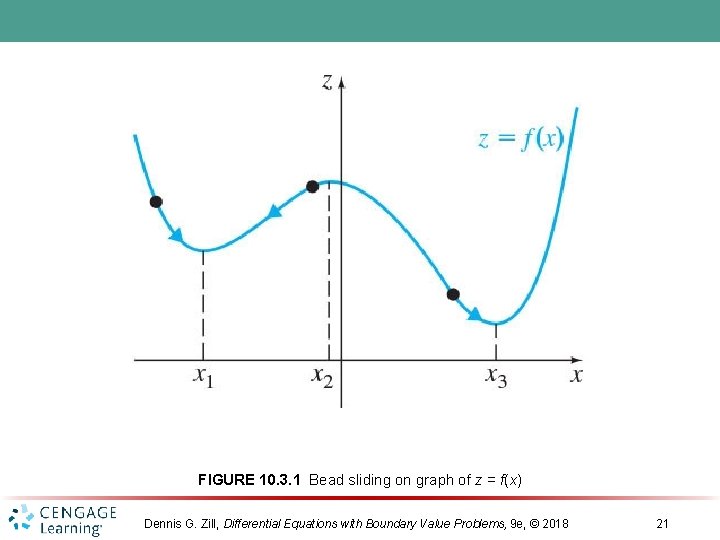
FIGURE 10. 3. 1 Bead sliding on graph of z = f(x) Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 21

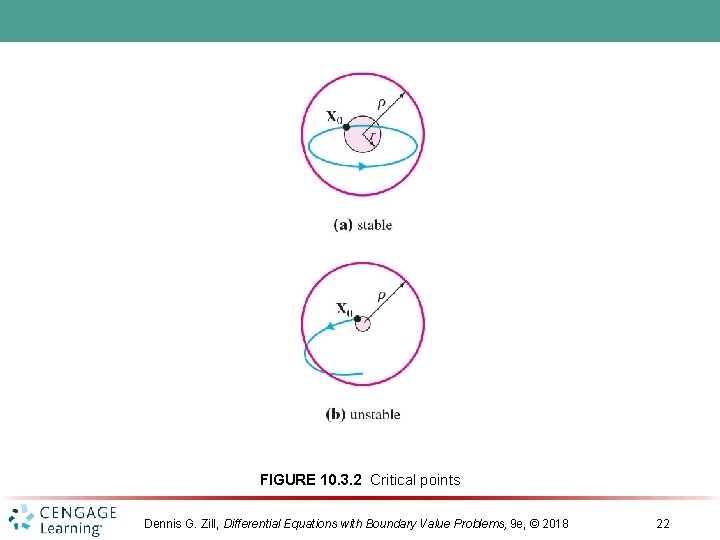
FIGURE 10. 3. 2 Critical points Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 22

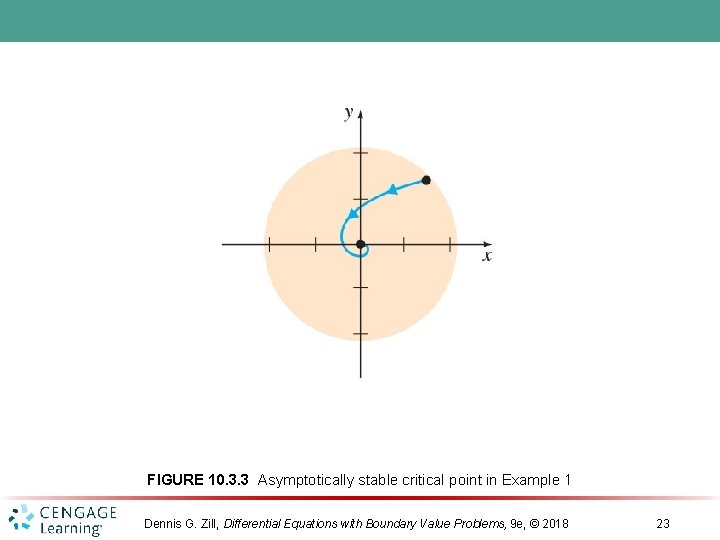
FIGURE 10. 3. 3 Asymptotically stable critical point in Example 1 Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 23

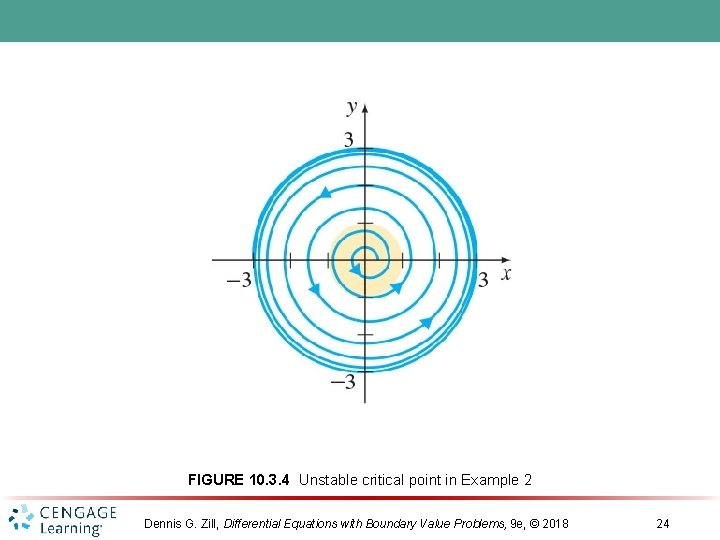
FIGURE 10. 3. 4 Unstable critical point in Example 2 Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 24

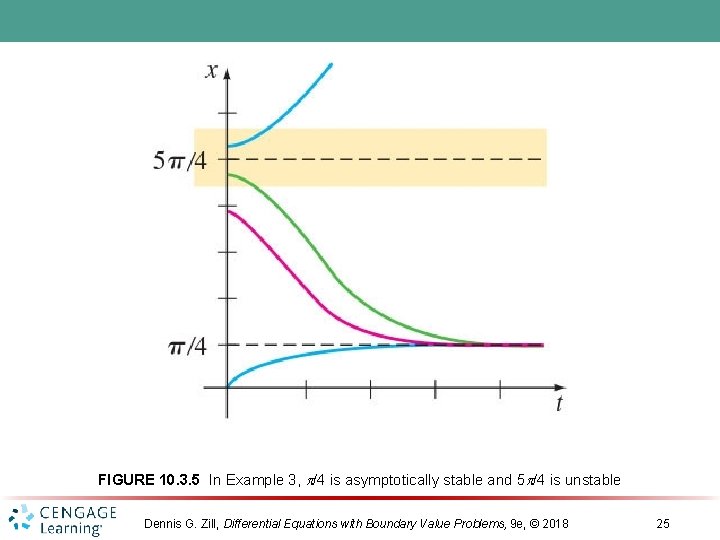
FIGURE 10. 3. 5 In Example 3, /4 is asymptotically stable and 5 /4 is unstable Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 25

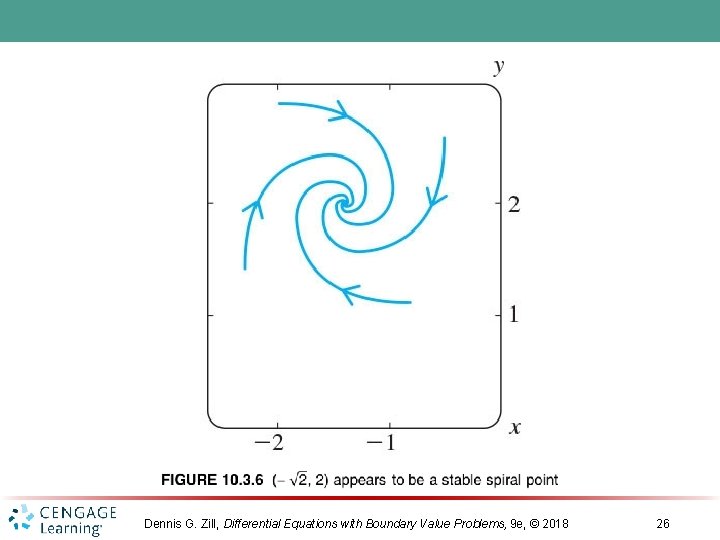
Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 26

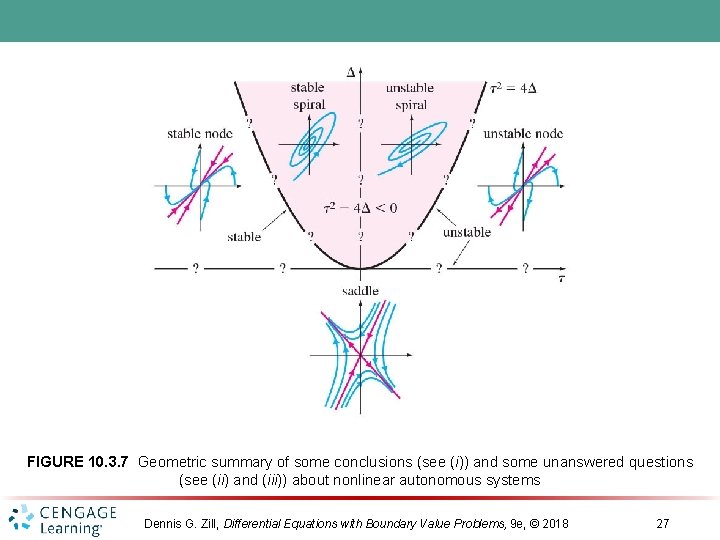
FIGURE 10. 3. 7 Geometric summary of some conclusions (see (i)) and some unanswered questions (see (ii) and (iii)) about nonlinear autonomous systems Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 27

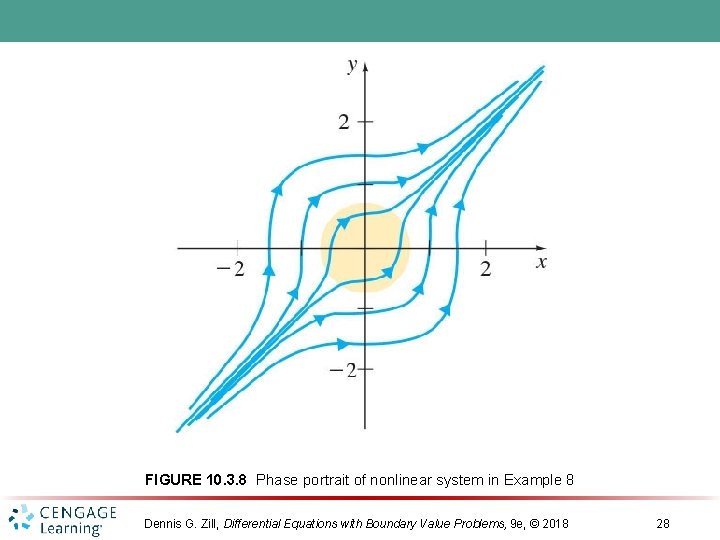
FIGURE 10. 3. 8 Phase portrait of nonlinear system in Example 8 Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 28

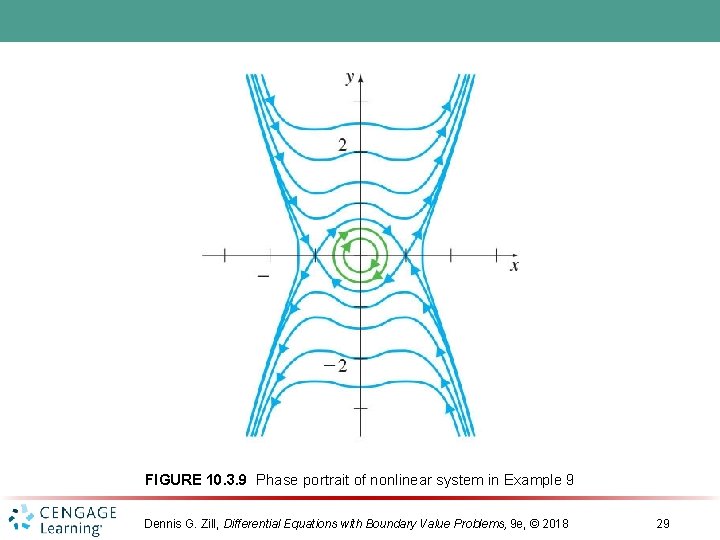
FIGURE 10. 3. 9 Phase portrait of nonlinear system in Example 9 Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 29

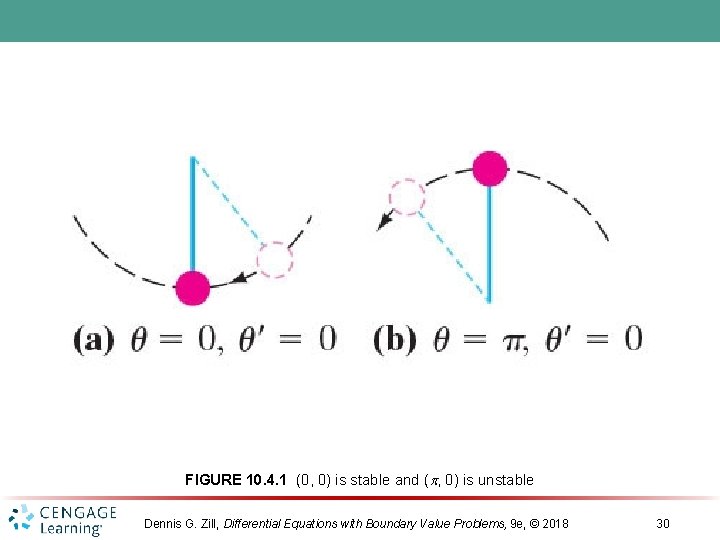
FIGURE 10. 4. 1 (0, 0) is stable and ( , 0) is unstable Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 30

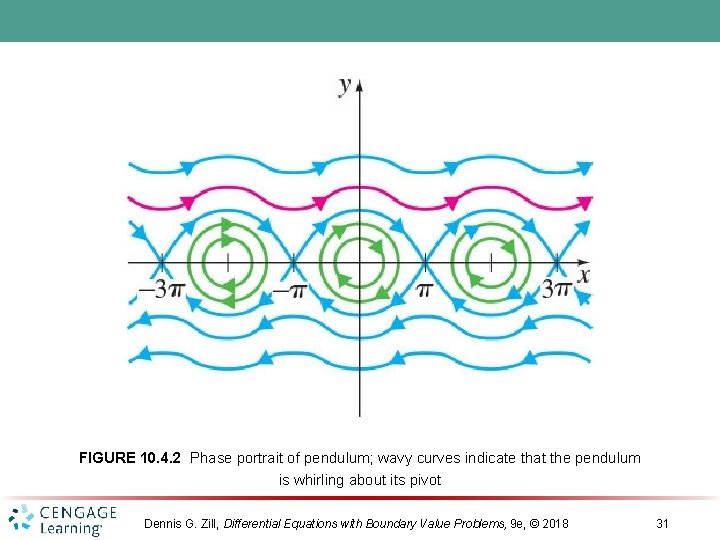
FIGURE 10. 4. 2 Phase portrait of pendulum; wavy curves indicate that the pendulum is whirling about its pivot Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 31

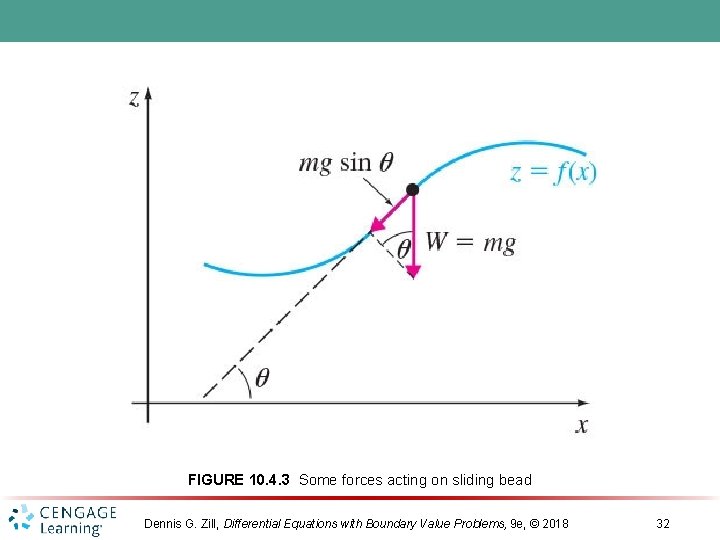
FIGURE 10. 4. 3 Some forces acting on sliding bead Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 32

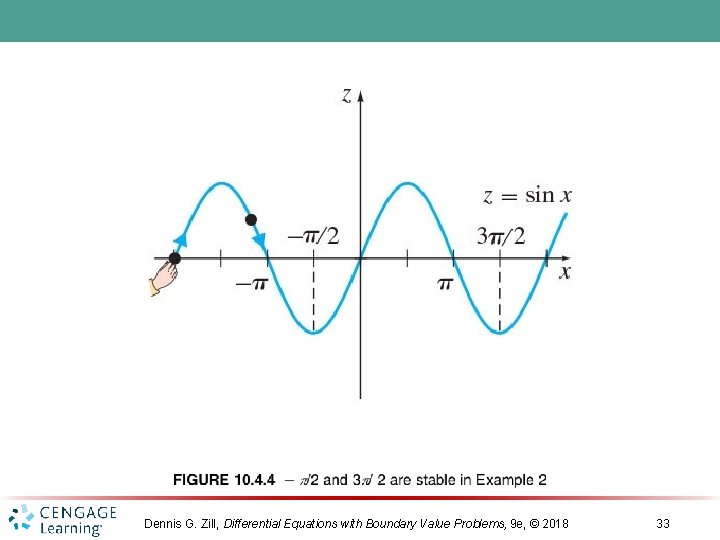
Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 33

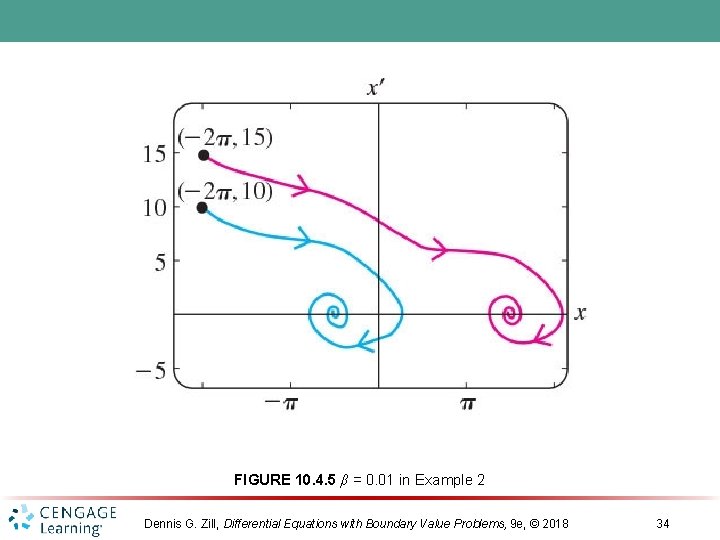
FIGURE 10. 4. 5 β = 0. 01 in Example 2 Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 34

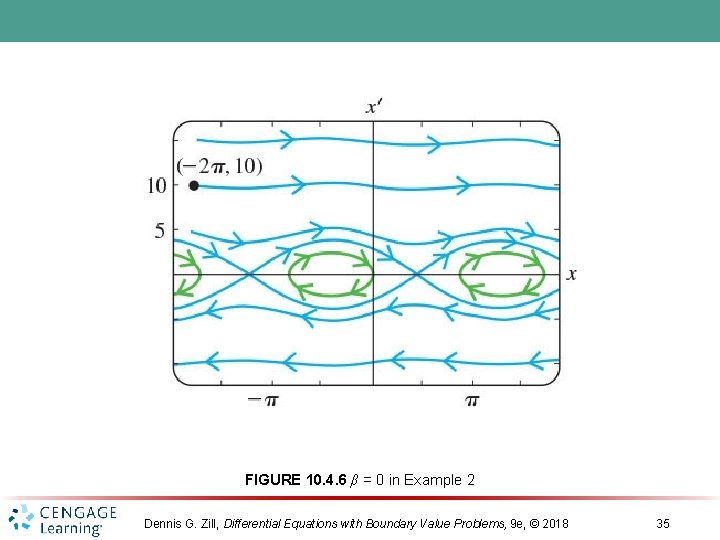
FIGURE 10. 4. 6 β = 0 in Example 2 Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 35

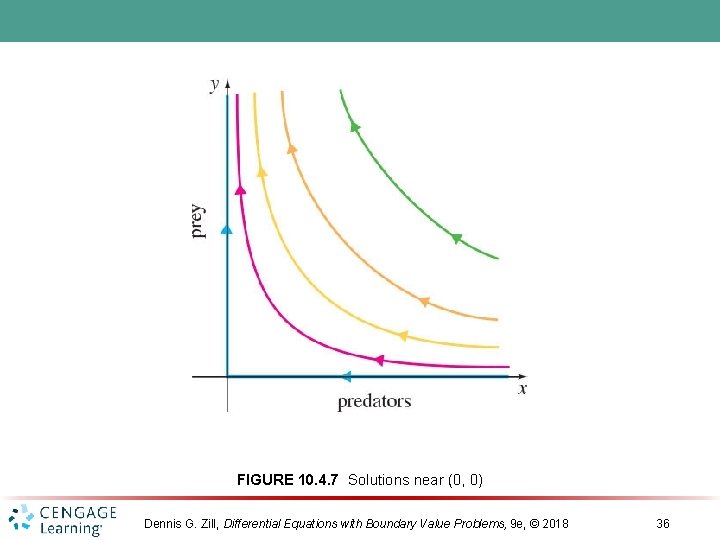
FIGURE 10. 4. 7 Solutions near (0, 0) Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 36

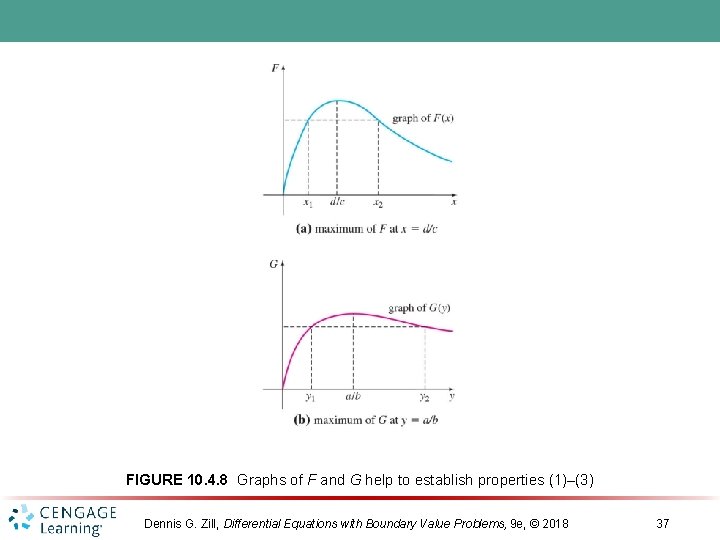
FIGURE 10. 4. 8 Graphs of F and G help to establish properties (1)–(3) Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 37

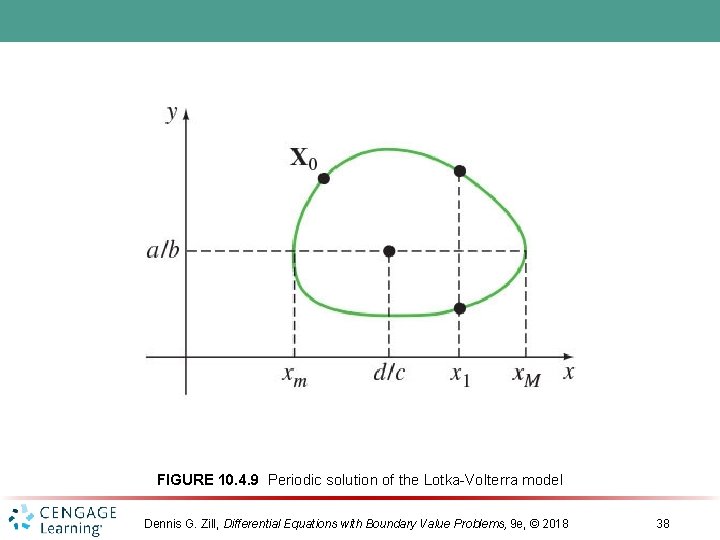
FIGURE 10. 4. 9 Periodic solution of the Lotka-Volterra model Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 38

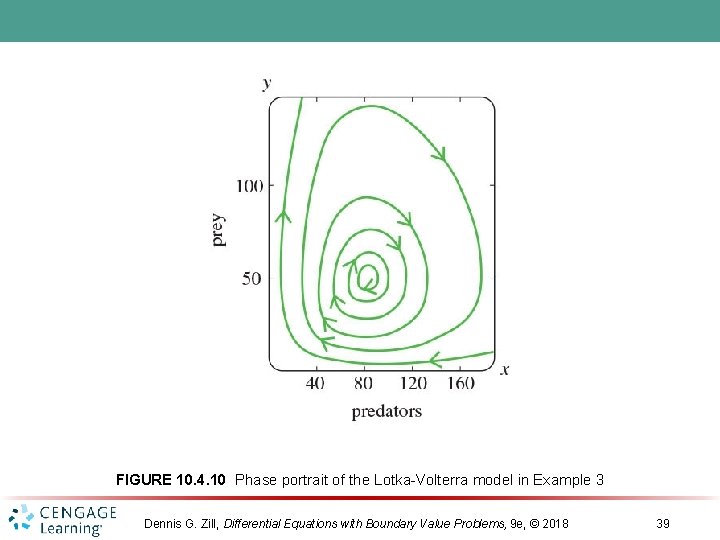
FIGURE 10. 4. 10 Phase portrait of the Lotka-Volterra model in Example 3 Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 39

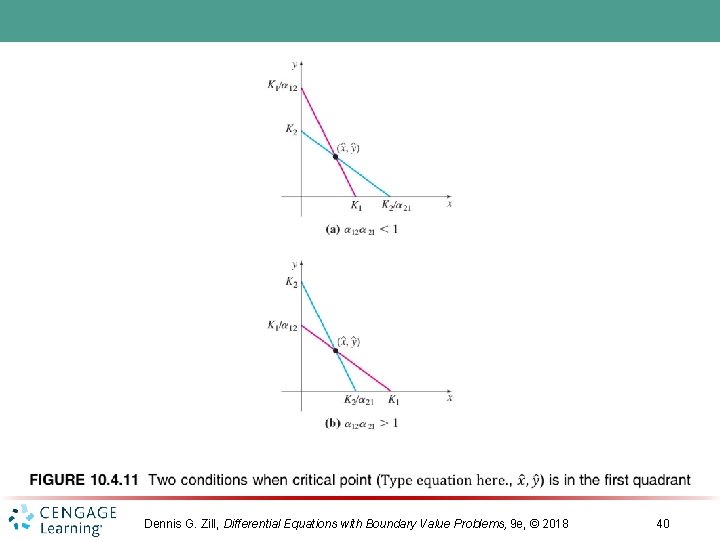
Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 40

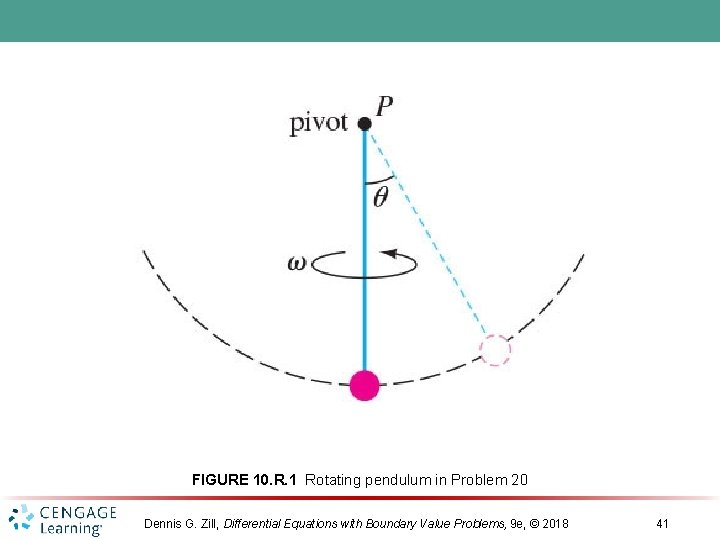
FIGURE 10. R. 1 Rotating pendulum in Problem 20 Dennis G. Zill, Differential Equations with Boundary Value Problems, 9 e, © 2018 41