Chapter 10 Sorting Algorithms Data Structures Using C

Chapter 10 Sorting Algorithms Data Structures Using C++ 1

Chapter Objectives • Learn the various sorting algorithms • Explore how to implement the selection, insertion, quick, merge, and heap sorting algorithms • Discover how the sorting algorithms discussed in this chapter perform • Learn how priority queues are implemented Data Structures Using C++ 2

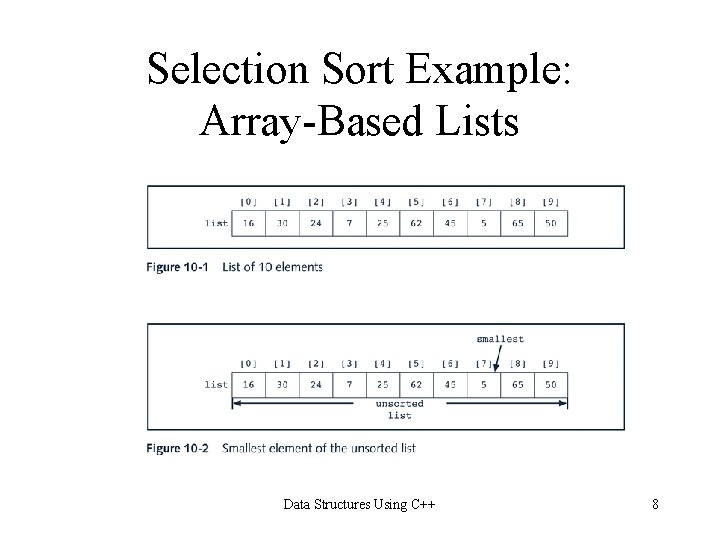
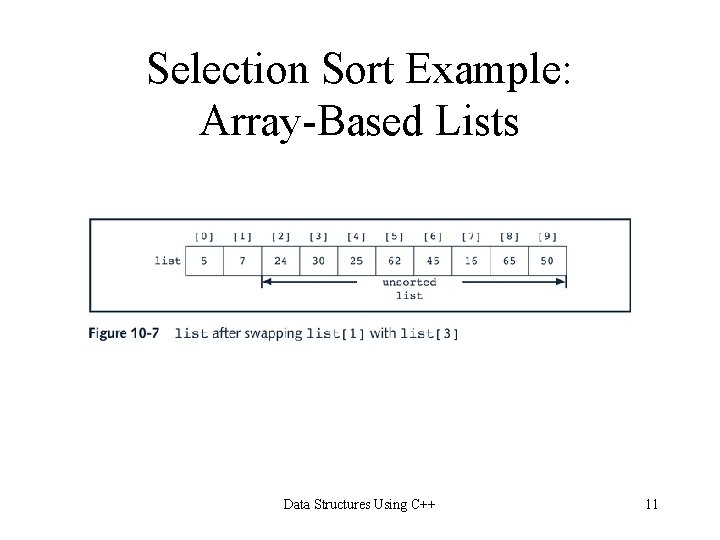
Selection Sort • Sorts list by 1. Finding smallest (or equivalently largest) element in the list 2. Moving it to the beginning (or end) of the list by swapping it with element in beginning (or end) position Data Structures Using C++ 3

class ordered. Array. List. Type template<class elem. Type> class ordered. Array. List. Type: public array. List. Type { public: void selection. Sort(); . . . }; Data Structures Using C++ 4

Smallest Element in List Function template<class elem. Type> int ordered. Array. List. Type<elem. Type>: : min. Location(int first, int last) { int loc, min. Index; min. Index = first; for(loc = first + 1; loc <= last; loc++) if(list[loc] < list[min. Index]) min. Index = loc; return min. Index; }//end min. Location Data Structures Using C++ 5

Swap Function template<class elem. Type> void ordered. Array. List. Type<elem. Type>: : swap(int first, int second) { elem. Type temp; temp = list[first]; list[first] = list[second]; list[second] = temp; }//end swap Data Structures Using C++ 6

Selection Sort Function template<class elem. Type> void ordered. Array. List. Type<elem. Type>: : selection. Sort() { int loc, min. Index; for(loc = 0; loc < length - 1; loc++) { min. Index = min. Location(loc, length - 1); swap(loc, min. Index); } } Data Structures Using C++ 7

Selection Sort Example: Array-Based Lists Data Structures Using C++ 8

Selection Sort Example: Array-Based Lists Data Structures Using C++ 9

Selection Sort Example: Array-Based Lists Data Structures Using C++ 10

Selection Sort Example: Array-Based Lists Data Structures Using C++ 11

Analysis: Selection Sort By analyzing the number of key comparisons, we see that selection sort is an O(n 2) algorithm: Data Structures Using C++ 12

class ordered. Array. List. Type template<class elem. Type> class ordered. Array. List. Type: public array. List. Type<elem. Type> { public: void insert. Ord(const elem. Type&); int binary. Search(const elem. Type& item); void selection. Sort(); ordered. Array. List. Type(int size = 100); private: void swap(int first, int second); int min. Location(int first, int last); }; Data Structures Using C++ 13

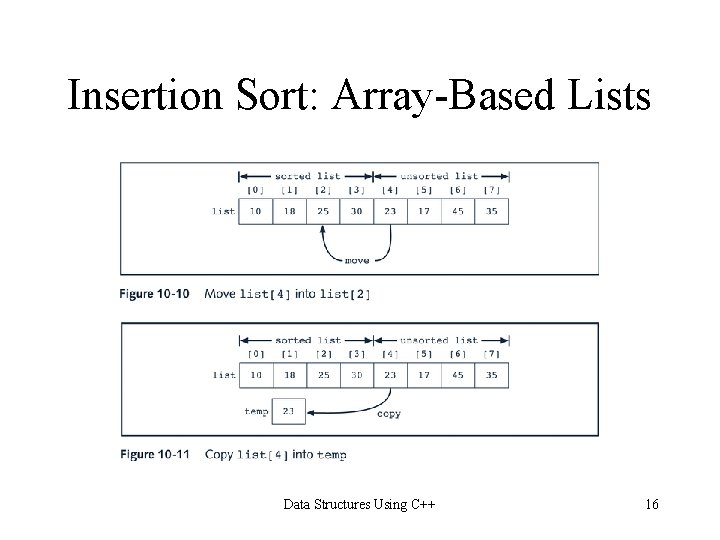
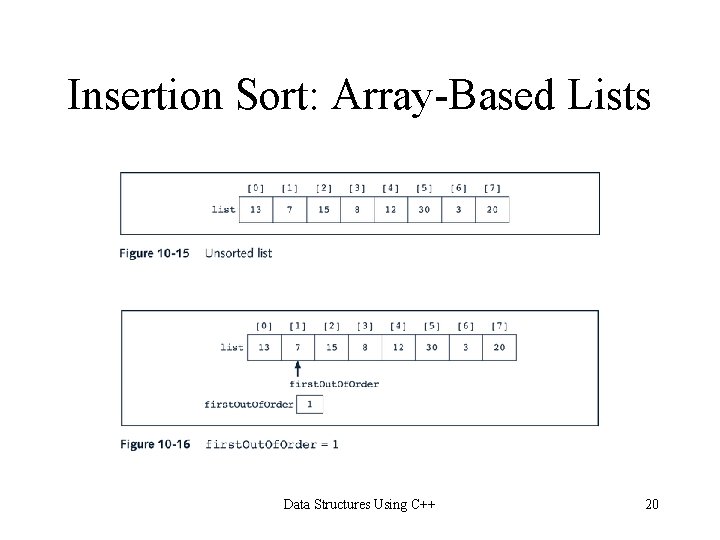
Insertion Sort • Reduces number of key comparisons made in selection sort • Can be applied to both arrays and linked lists (examples follow) • Sorts list by – Finding first unsorted element in list – Moving it to its proper position Data Structures Using C++ 14

Insertion Sort: Array-Based Lists Data Structures Using C++ 15

Insertion Sort: Array-Based Lists Data Structures Using C++ 16

Insertion Sort: Array-Based Lists Data Structures Using C++ 17

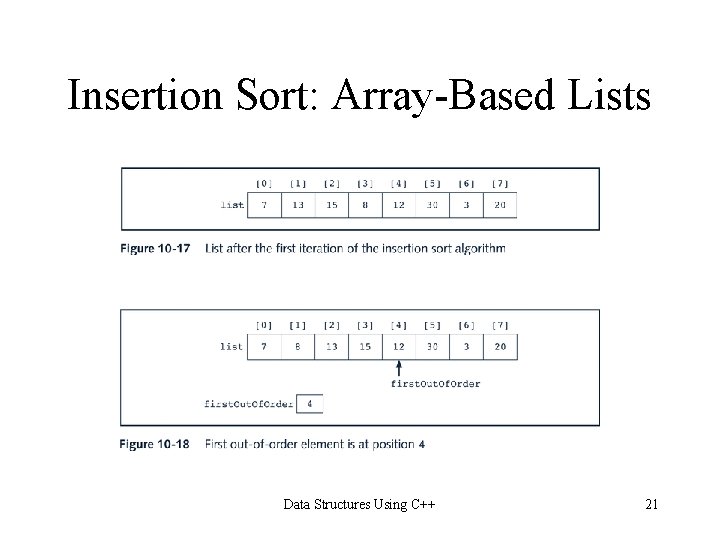
Insertion Sort: Array-Based Lists Data Structures Using C++ 18

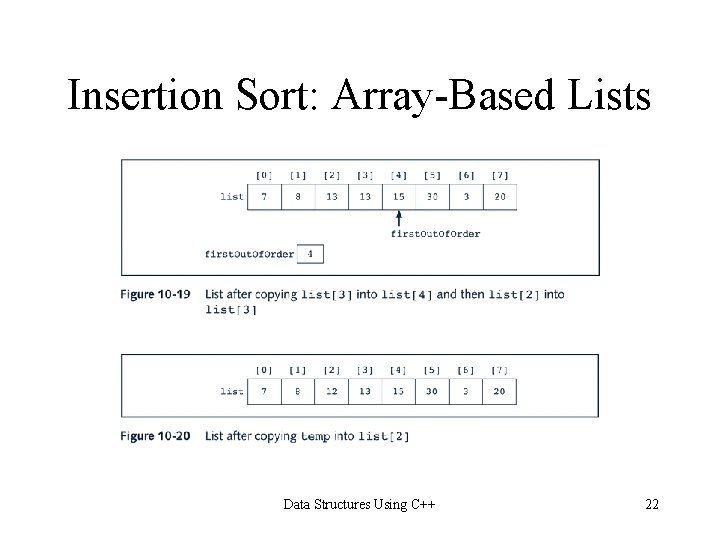
Insertion Sort: Array-Based Lists for(first. Out. Of. Order = 1; first. Out. Of. Order < length; first. Out. Of. Order++) if(list[first. Out. Of. Order] is less than list[first. Out. Of. Order - 1]) { copy list[first. Out. Of. Order] into temp initialize location to first. Out. Of. Order do { a. move list[location - 1] one array slot down b. decrement location by 1 to consider the next element of the sorted portion of the array } while(location > 0 && the element in the upper sublist at location - 1 is greater than temp) } copy temp into list[location] Data Structures Using C++ 19

Insertion Sort: Array-Based Lists Data Structures Using C++ 20

Insertion Sort: Array-Based Lists Data Structures Using C++ 21

Insertion Sort: Array-Based Lists Data Structures Using C++ 22

Insertion Sort: Array-Based Lists template<class elem. Type> void ordered. Array. List. Type<elem. Type>: : insertion. Sort() { int first. Out. Of. Order, location; elem. Type temp; for(first. Out. Of. Order = 1; first. Out. Of. Order < length; first. Out. Of. Order++) if(list[first. Out. Of. Order] < list[first. Out. Of. Order - 1]) { temp = list[first. Out. Of. Order]; location = first. Out. Of. Order; do { list[location] = list[location - 1]; location--; }while(location > 0 && list[location - 1] > temp); list[location] = temp; } }//end insertion. Sort Data Structures Using C++ 23

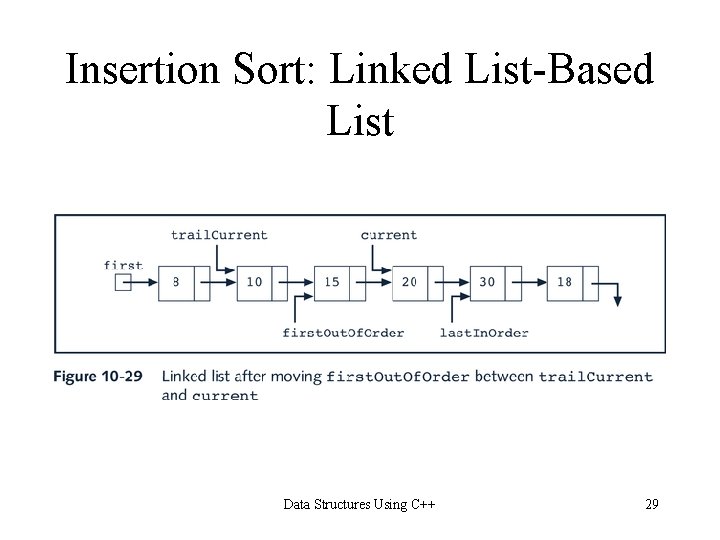
Insertion Sort: Linked List-Based List Data Structures Using C++ 24

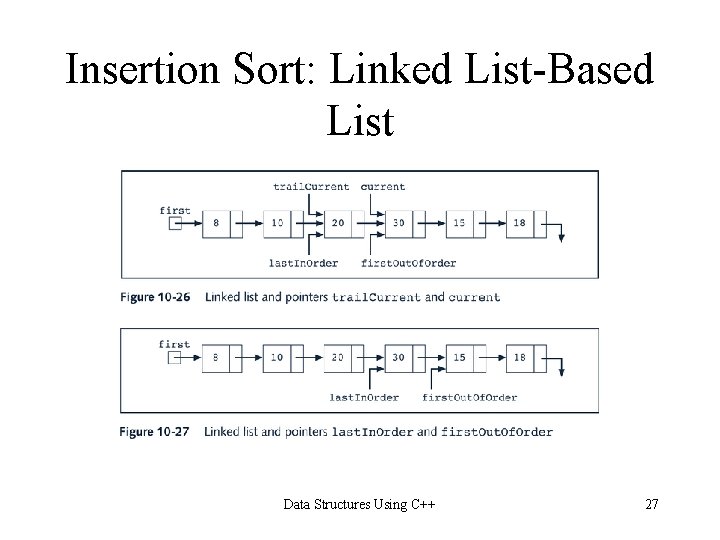
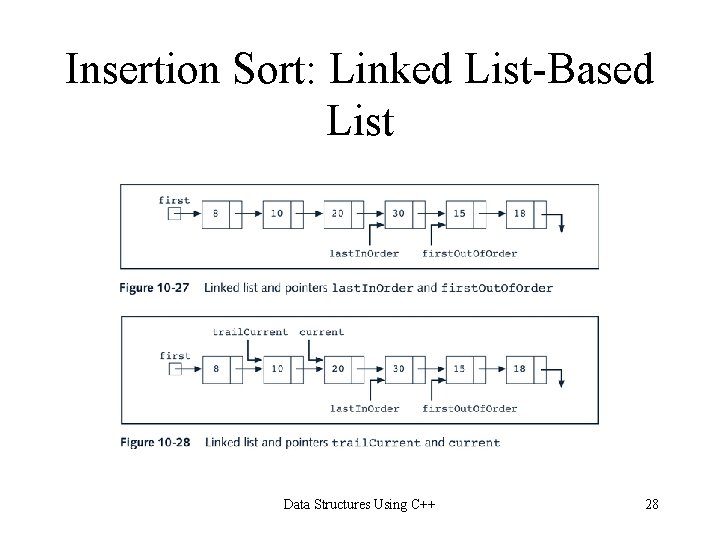
Insertion Sort: Linked List-Based List if(first. Out. Of. Order->info is less than first->info) move first. Out. Of. Order before first else { set trail. Current to first set current to the second node in the list //search the list while(current->info is less than first. Out. Of. Order->info) { advance trail. Current; advance current; } if(current is not equal to first. Out. Of. Order) { //insert first. Out. Of. Order between current and trail. Current last. In. Order->link = first. Out. Of. Order->link; first. Out. Of. Order->link = current; trail. Current->link = first. Out. Of. Order; } else //first. Out. Of. Order is already at the first place last. In. Order = last. In. Order->link; } Data Structures Using C++ 25

Insertion Sort: Linked List-Based List Data Structures Using C++ 26

Insertion Sort: Linked List-Based List Data Structures Using C++ 27

Insertion Sort: Linked List-Based List Data Structures Using C++ 28

Insertion Sort: Linked List-Based List Data Structures Using C++ 29

Analysis: Insertion Sort Data Structures Using C++ 30

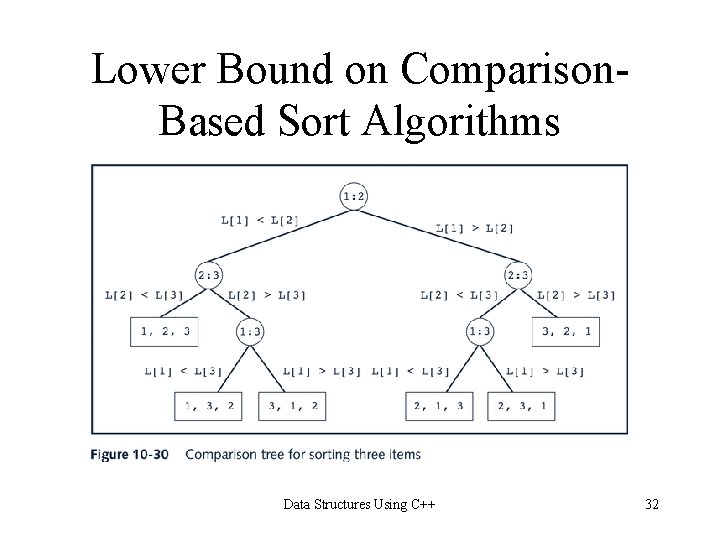
Lower Bound on Comparison. Based Sort Algorithms • Trace execution of comparison-based algorithm by using graph called comparison tree • Let L be a list of n distinct elements, where n > 0. For any j and k, where 1 = j, k = n, either L[j] < L[k] or L[j] > L[k] • Each comparison of the keys has two outcomes; comparison tree is a binary tree • Each comparison is a circle, called a node • Node is labeled as j: k, representing comparison of L[j] with L[k] • If L[j] < L[k], follow the left branch; otherwise, follow the right branch Data Structures Using C++ 31

Lower Bound on Comparison. Based Sort Algorithms Data Structures Using C++ 32

Lower Bound on Comparison. Based Sort Algorithms • Top node in the figure is the root node • Straight line that connects the two nodes is called a branch • A sequence of branches from a node, x, to another node, y, is called a path from x to y • Rectangle, called a leaf, represents the final ordering of the nodes • Theorem: Let L be a list of n distinct elements. Any sorting algorithm that sorts L by comparison of the keys only, in its worst case, makes at least O(n*log 2 n) key comparisons Data Structures Using C++ 33

Quick Sort • Recursive algorithm • Uses the divide-and-conquer technique to sort a list • List is partitioned into two sublists, and the two sublists are then sorted and combined into one list in such a way so that the combined list is sorted Data Structures Using C++ 34

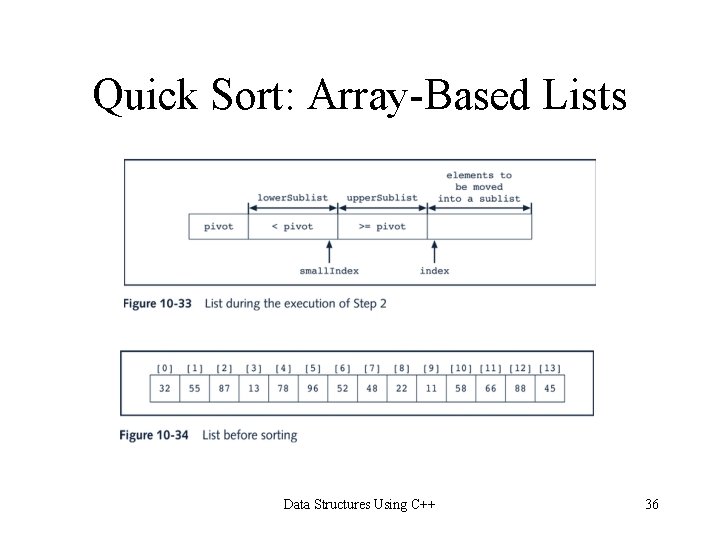
Quick Sort: Array-Based Lists Data Structures Using C++ 35

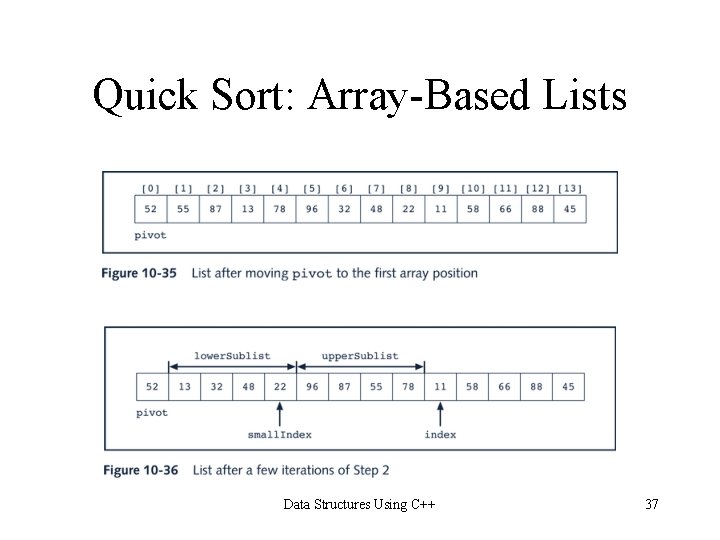
Quick Sort: Array-Based Lists Data Structures Using C++ 36

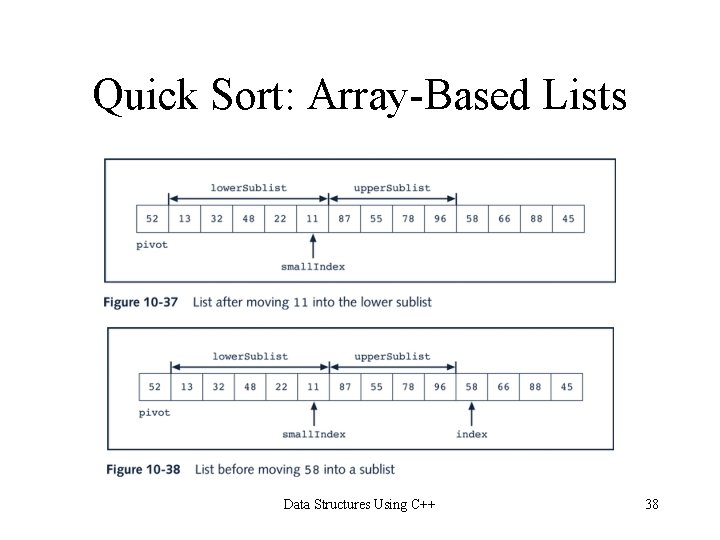
Quick Sort: Array-Based Lists Data Structures Using C++ 37

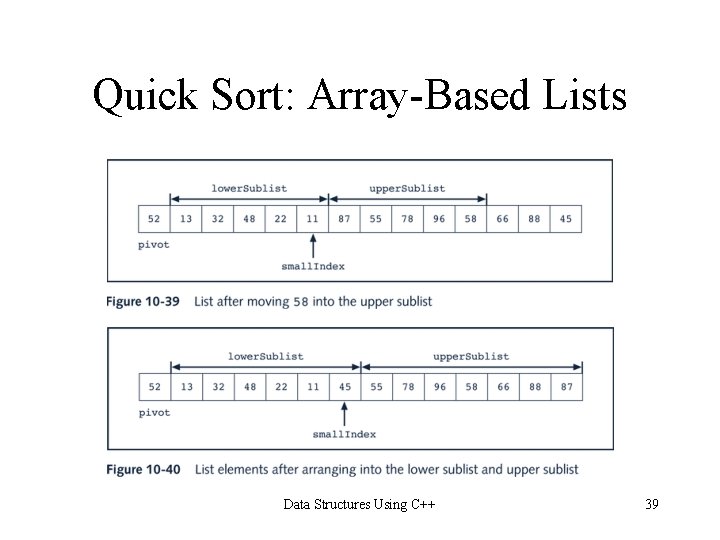
Quick Sort: Array-Based Lists Data Structures Using C++ 38

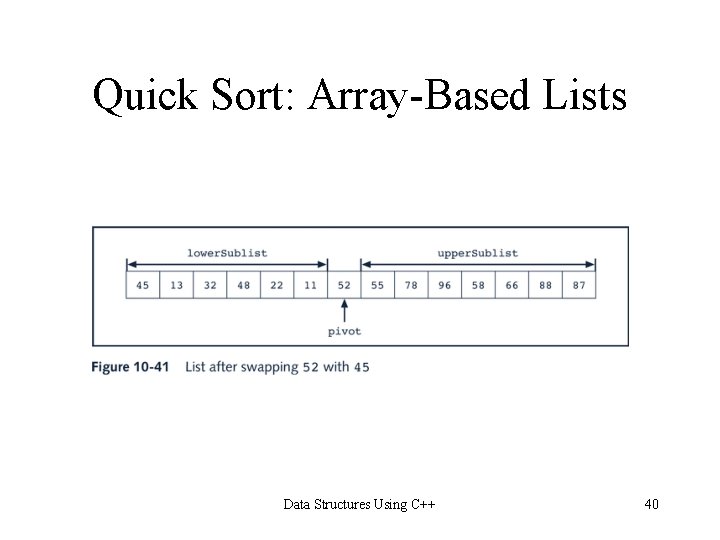
Quick Sort: Array-Based Lists Data Structures Using C++ 39

Quick Sort: Array-Based Lists Data Structures Using C++ 40

Quick Sort: Array-Based Lists template<class elem. Type> int ordered. Array. List. Type<elem. Type>: : partition(int first, int last) { elem. Type pivot; int index, small. Index; swap(first, (first + last)/2); pivot = list[first]; small. Index = first; for(index = first + 1; index <= last; index++) if(list[index] < pivot) { small. Index++; swap(small. Index, index); } swap(first, small. Index); return small. Index; } Data Structures Using C++ 41

Quick Sort: Array-Based Lists template<class elem. Type> void ordered. Array. List. Type<elem. Type>: : swap(int first, int second) { elem. Type temp; temp = list[first]; list[first] = list[second]; list[second] = temp; } //end swap Data Structures Using C++ 42

Quick Sort: Array-Based Lists template<class elem. Type> void ordered. Array. List. Type<elem. Type>: : rec. Quick. Sort(int first, int last) { int pivot. Location; if(first <last) { pivot. Location = partition(first, last); rec. Quick. Sort(first, pivot. Location - 1); rec. Quick. Sort(pivot. Location + 1, last); } } //end rec. Quick. Sort template<class elem. Type> void ordered. Array. List. Type<elem. Type>: : quick. Sort() { rec. Quick. Sort(0, length - 1); }//end quick. Sort Data Structures Using C++ 43

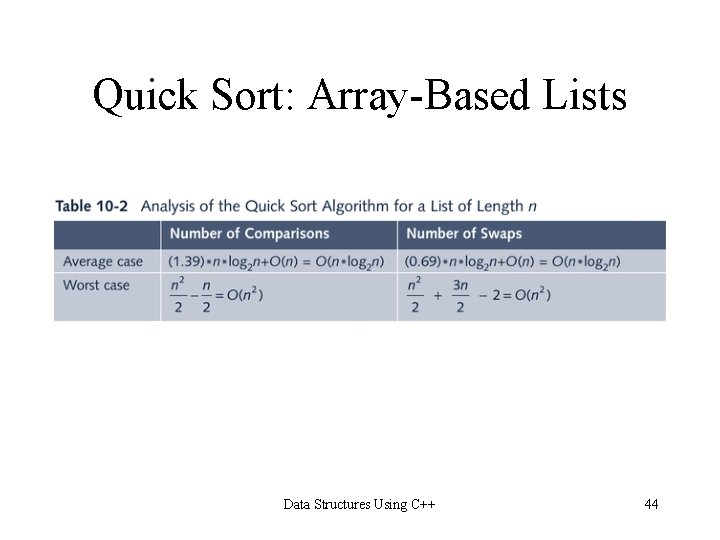
Quick Sort: Array-Based Lists Data Structures Using C++ 44

Merge Sort • Uses the divide-and-conquer technique to sort a list • Merge sort algorithm also partitions the list into two sublists, sorts the sublists, and then combines the sorted sublists into one sorted list Data Structures Using C++ 45

Merge Sort Algorithm Data Structures Using C++ 46

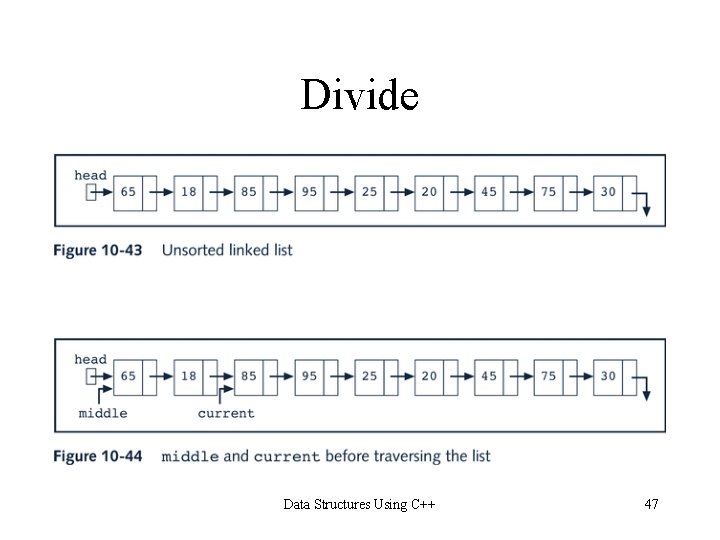
Divide Data Structures Using C++ 47

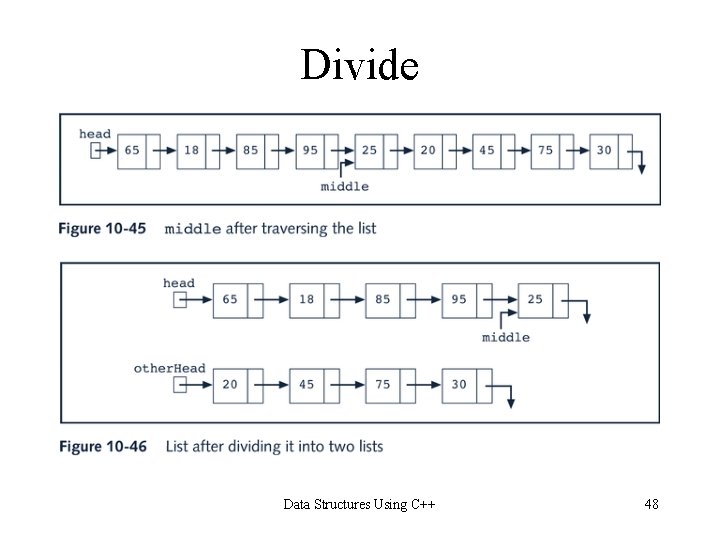
Divide Data Structures Using C++ 48

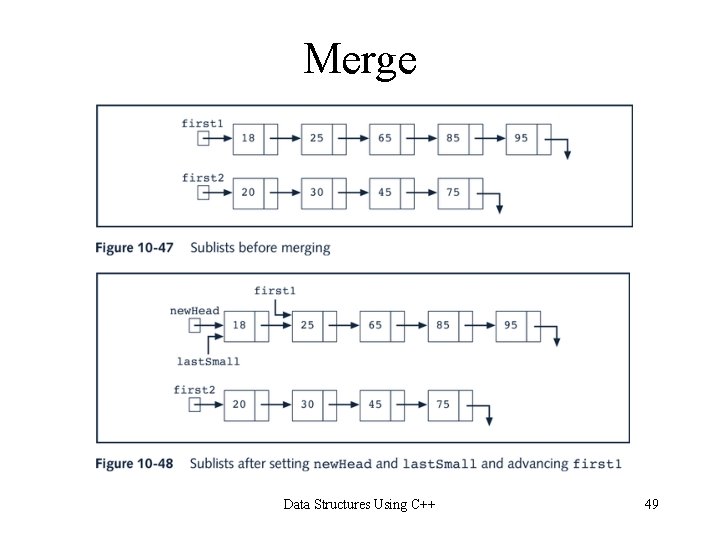
Merge Data Structures Using C++ 49

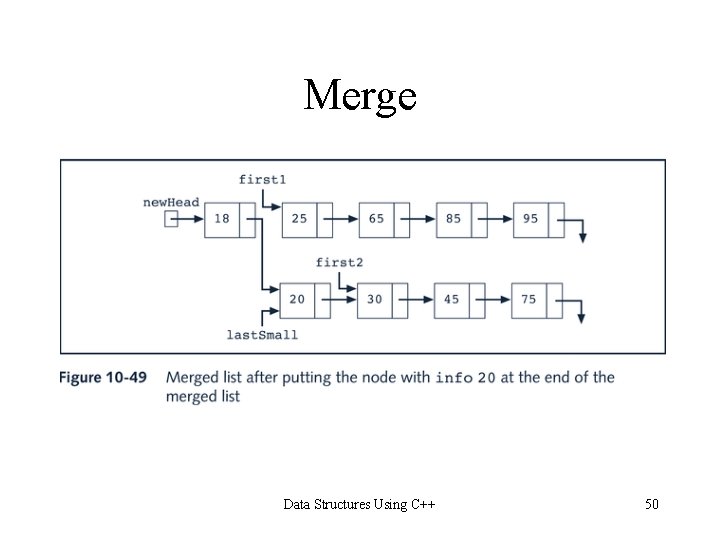
Merge Data Structures Using C++ 50

Analysis of Merge Sort Suppose that L is a list of n elements, where n > 0. Let A(n) denote the number of key comparisons in the average case, and W(n) denote the number of key comparisons in the worst case to sort L. It can be shown that: A(n) = n*log 2 n – 1. 26 n = O(n*log 2 n) W(n) = n*log 2 n – (n– 1) = O(n*log 2 n) Data Structures Using C++ 51

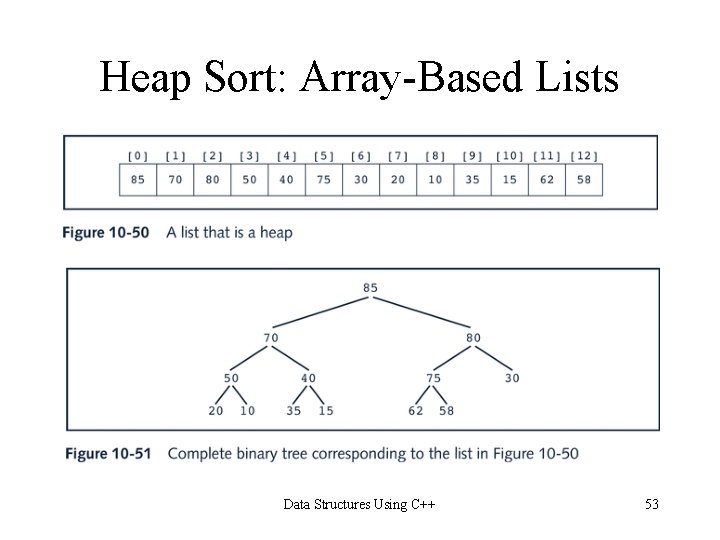
Heap Sort • Definition: A heap is a list in which each element contains a key, such that the key in the element at position k in the list is at least as large as the key in the element at position 2 k + 1 (if it exists), and 2 k + 2 (if it exists) Data Structures Using C++ 52

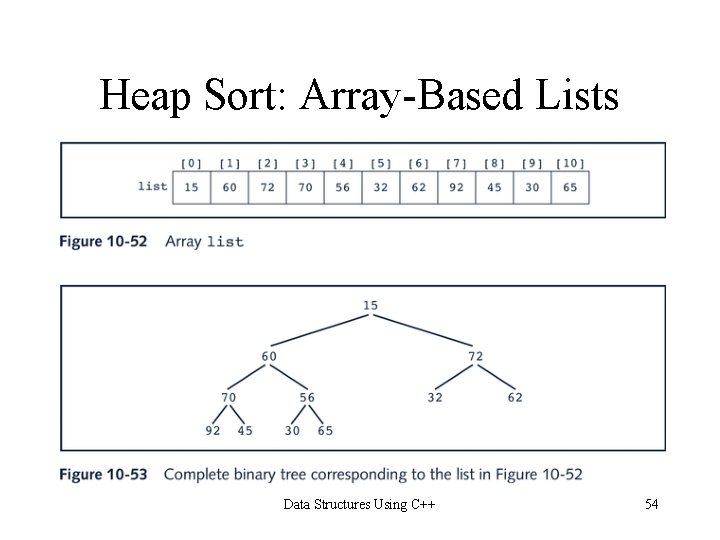
Heap Sort: Array-Based Lists Data Structures Using C++ 53

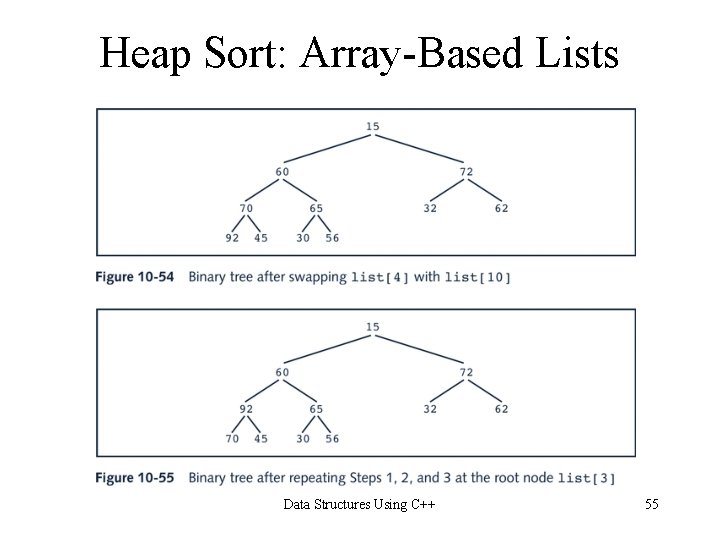
Heap Sort: Array-Based Lists Data Structures Using C++ 54

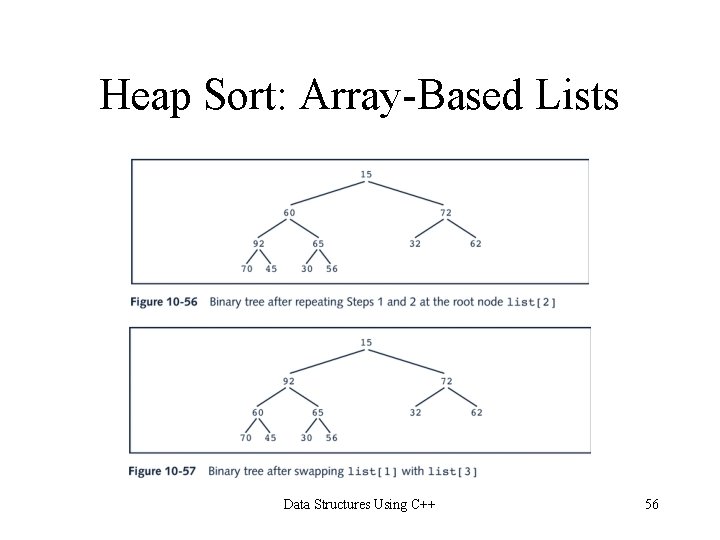
Heap Sort: Array-Based Lists Data Structures Using C++ 55

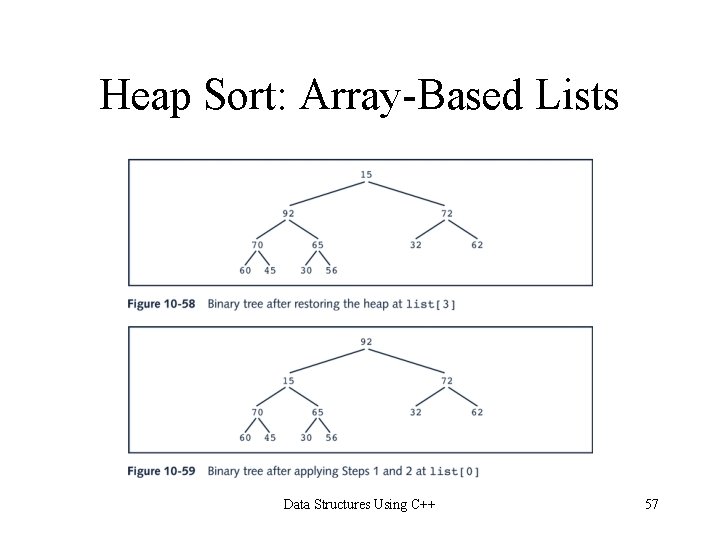
Heap Sort: Array-Based Lists Data Structures Using C++ 56

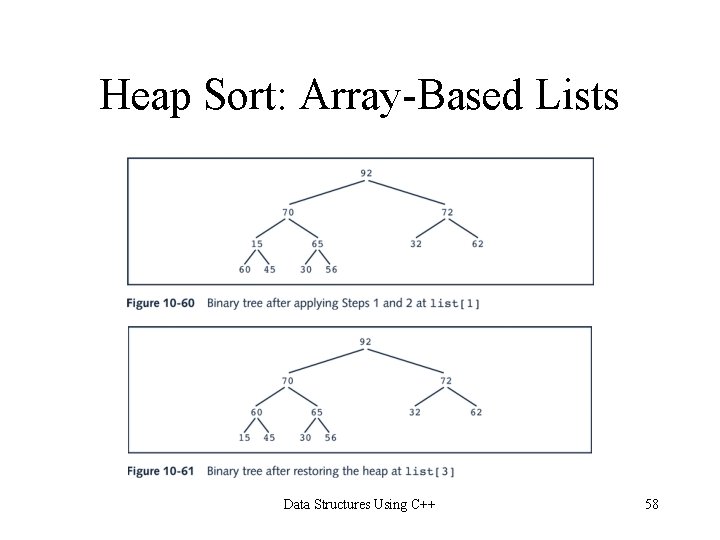
Heap Sort: Array-Based Lists Data Structures Using C++ 57

Heap Sort: Array-Based Lists Data Structures Using C++ 58

Priority Queues: Insertion Assuming the priority queue is implemented as a heap: 1. Insert the new element in the first available position in the list. (This ensures that the array holding the list is a complete binary tree. ) 2. After inserting the new element in the heap, the list may no longer be a heap. So to restore the heap: while (parent of new entry < new entry) swap the parent with the new entry Data Structures Using C++ 59

Priority Queues: Remove Assuming the priority queue is implemented as a heap, to remove the first element of the priority queue: 1. Copy the last element of the list into the first array position. 2. Reduce the length of the list by 1. 3. Restore the heap in the list. Data Structures Using C++ 60

Chapter Summary • Sorting Algorithms – Selection sort – Insertion sort – Quick sort – Merge sort – heap sort • Algorithm analysis • Priority queues Data Structures Using C++ 61