Chapter 10 Screening for Disease 1 Terminology Reliability

Chapter 10 Screening for Disease 1

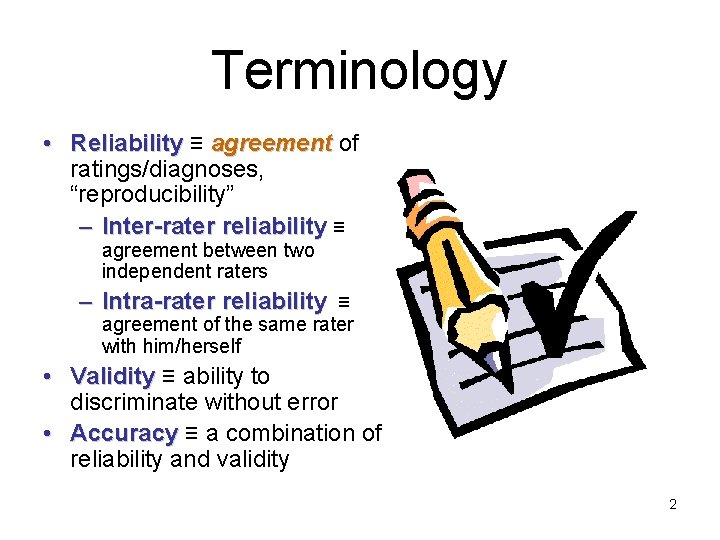
Terminology • Reliability ≡ agreement of ratings/diagnoses, “reproducibility” – Inter-rater reliability ≡ agreement between two independent raters – Intra-rater reliability ≡ agreement of the same rater with him/herself • Validity ≡ ability to discriminate without error • Accuracy ≡ a combination of reliability and validity 2

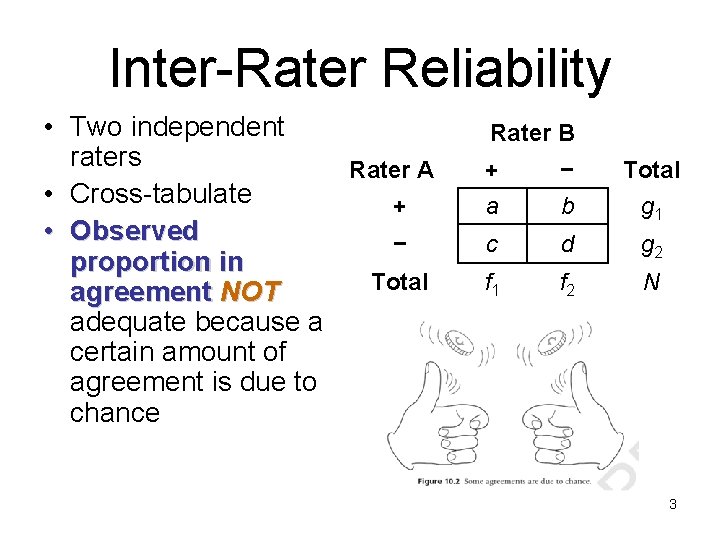
Inter-Rater Reliability • Two independent raters Rater A • Cross-tabulate + • Observed − proportion in Total agreement NOT adequate because a certain amount of agreement is due to chance Rater B + − Total a b g 1 c d g 2 f 1 f 2 N 3

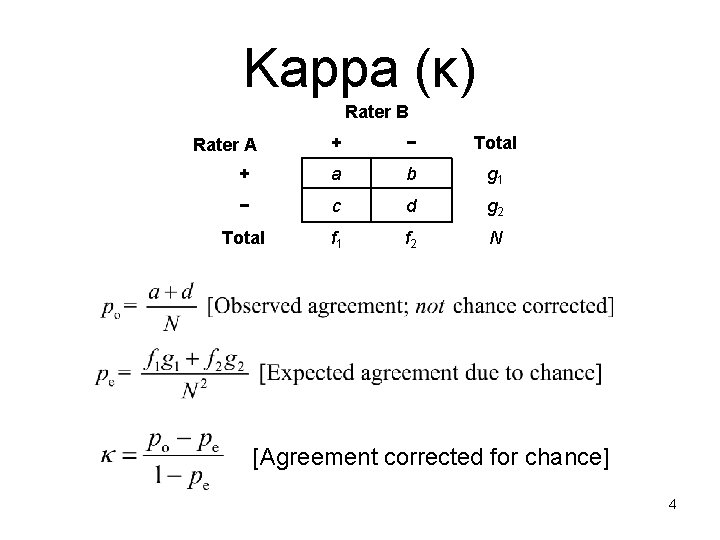
Kappa (κ) Rater B + − Total + a b g 1 − c d g 2 Total f 1 f 2 N Rater A [Agreement corrected for chance] 4

κ Benchmarks 5

Example 1: Flip two coins To what extent are results reproducible? Toss B Toss A Heads Tails Total Heads 25 25 50 Tails 25 25 50 Total 50 50 100 6

Example 2 To what extent are these diagnoses reproducible? Rater B Rater A + − Total + 20 4 24 − 5 71 76 Total 25 75 100 “substantial” agreement 7

§ 10. 3 Validity • Compare screening test results to a gold standard (“definitive diagnosis”) • Each patient is classified as either true positive (TP), true negative (TN), false positive (FP), or false negative (FN) Test T+ T− Total D+ D− Total TP FN TP+FN FP TN FP+TN TP+FP FN+TN N 8

Sensitivity Test T+ T− Total D+ TP FN TP+FN D− FP TN FP+TN Total TP+FP FN+TN N SEN ≡ proportion of cases that test positive 9

Specificity Test T+ T− Total D+ D− Total TP FN TP+FN FP TN FP+TN TP+FP FN+TN N SPEC ≡ proportion of noncases that test negative 10

Predictive Value Positive Test T+ T− Total D+ TP FN TP+FN D− FP TN FP+TN Total TP+FP FN+TN N PVP ≡ proportion of positive tests that are true cases 11

Predictive Value Negative Test T+ T− Total D+ TP FN TP+FN D− FP TN FP+TN Total TP+FP FN+TN N PVN ≡ proportion of negative tests that are true non-cases 12

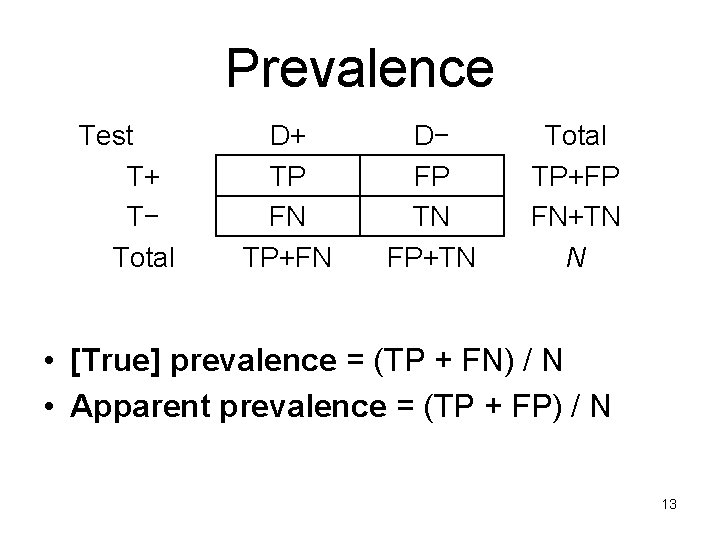
Prevalence Test T+ T− Total D+ TP FN TP+FN D− FP TN FP+TN Total TP+FP FN+TN N • [True] prevalence = (TP + FN) / N • Apparent prevalence = (TP + FP) / N 13

Conditional Probability Notation • Pr(A|B) ≡ “the probability of A given B” • For example Pr(T+|D+) ≡ “probability test positive given disease positive” = SENsitivity • SPEC ≡ Pr(T−|D−) • PVP = Pr(D+|T+) • PVN= Pr(D−|T−) 14

Example Low Prevalence Population Conditions: N = 1, 000; Prevalence =. 001 D+ D− Total T+ T− Total 1000 1, 000 Prevalence = (those with disease) / N Therefore: (Those with disease) = Prevalence × N =. 001× 1, 000 = 1000 15

Example: Low Prevalence Population Number of non-cases, i. e. , TN + FP D+ D− Total 1000 999, 000 1, 000 T+ T− Total 1, 000 – 1, 000 = 999, 000 16

Example: Low Prevalence Population Assume test SENsitivity =. 99, i. e. , Test will pick up 99% of those with disease T+ T− Total D+ 990 D− Total 1000 TP = SEN × (those with disease) = 0. 99 × 1000 = 990 17

Example: Low Prevalence Population It follows that: T+ D+ 990 T− 10 Total 1000 D− Total FN = 1000 – 990 = 10 18

Example: Low Prevalence Population Suppose test SPECificity =. 99 i. e. , it will correctly identify 99% of the noncases D+ D− Total T+ T− 989, 010 Total 999, 000 TN = SPEC × (those without disease) = 0. 99 × 999, 000 = 989, 010 19

Example: Low Prevalence Population It follows that: D+ D− T+ 9, 990 T− Total 989, 010 999, 000 Total FPs = 999, 000 – 989, 010 = 9, 900 20

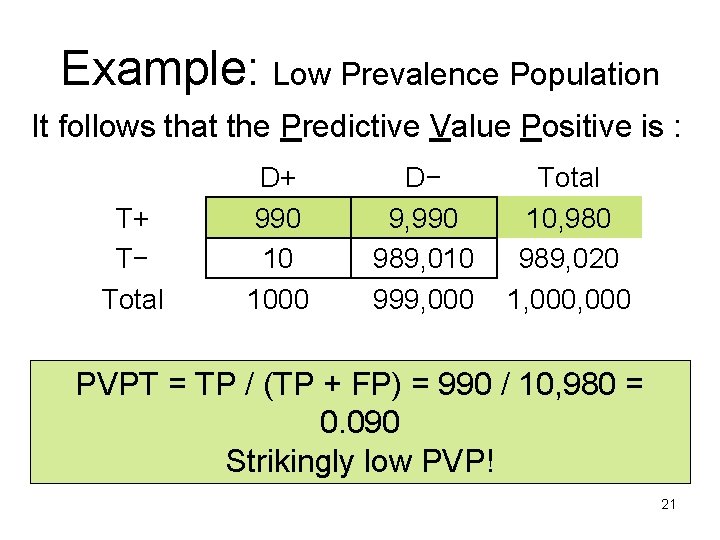
Example: Low Prevalence Population It follows that the Predictive Value Positive is : T+ T− Total D+ 990 10 1000 D− 9, 990 989, 010 999, 000 Total 10, 980 989, 020 1, 000 PVPT = TP / (TP + FP) = 990 / 10, 980 = 0. 090 Strikingly low PVP! 21

Example: Low Prevalence Population It follows that the Predictive Value Negative is: T+ T− Total D+ 990 10 1000 D− Total 9, 990 10, 980 989, 010 989, 020 999, 000 1, 000 PVNT= TN / (all those who test negative) = 989010 / 989020 =. 9999 22

Example: High prevalence population Same test parameters but used in population with true prevalence of. 10 D+ D− Total T+ 99, 000 108, 000 T− 1, 000 892, 000 Total 100, 000 900, 000 1, 000 Prev = 100000 / 1, 000 = 0. 10 SEN = 99000 / 100, 000 = 0. 99 SPEC = 891, 000 / 900, 000 = 0. 99 23

Example: High prevalence population An HIV screening test is used in one million people. Prevalence in population is now 10%. SEN and SPEC are again 99%. T+ T− Total D+ 99, 000 100, 000 D− 9, 000 891, 000 900, 000 Total 108, 000 892, 000 1, 000 Prevalence = 100000 / 1, 000 = 0. 10 PVP = 99, 000 / 108, 000 = 0. 92 PVN = 891, 000 / 892, 000 = 0. 9989 24

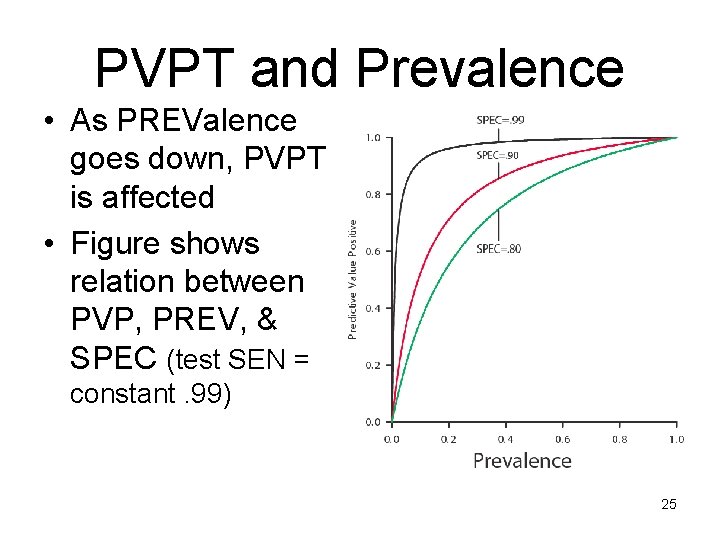
PVPT and Prevalence • As PREValence goes down, PVPT is affected • Figure shows relation between PVP, PREV, & SPEC (test SEN = constant. 99) 25

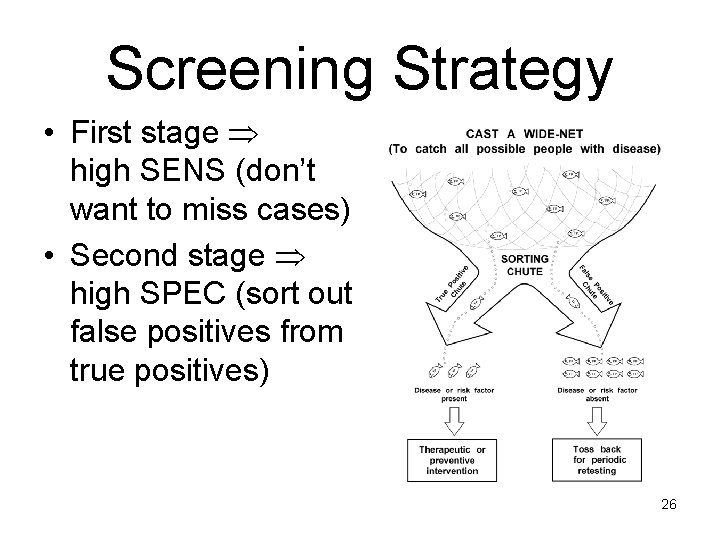
Screening Strategy • First stage high SENS (don’t want to miss cases) • Second stage high SPEC (sort out false positives from true positives) 26

Selecting a Cutoff Point • There is often an overlap in test results for diseased and non-diseased population • Sensitivity and specificity are influenced by the chosen cutoff point used to determine positive results • Example: Immunofluorescence test for HIV based on optical density ratio (next slide) 27

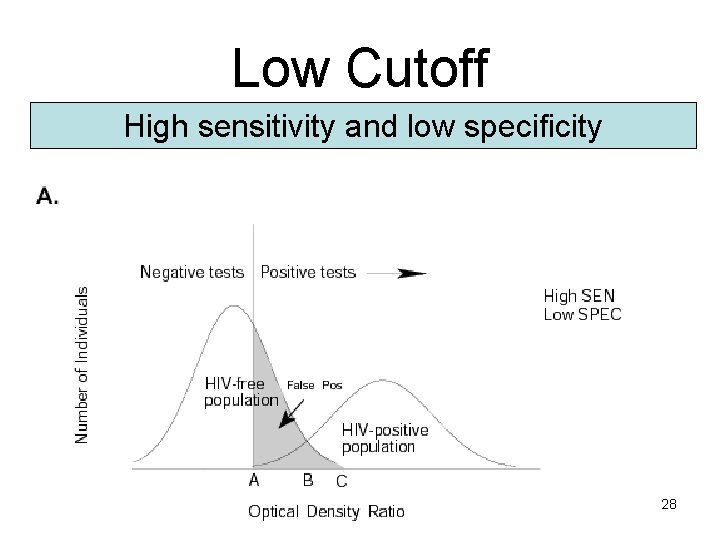
Low Cutoff High sensitivity and low specificity 28

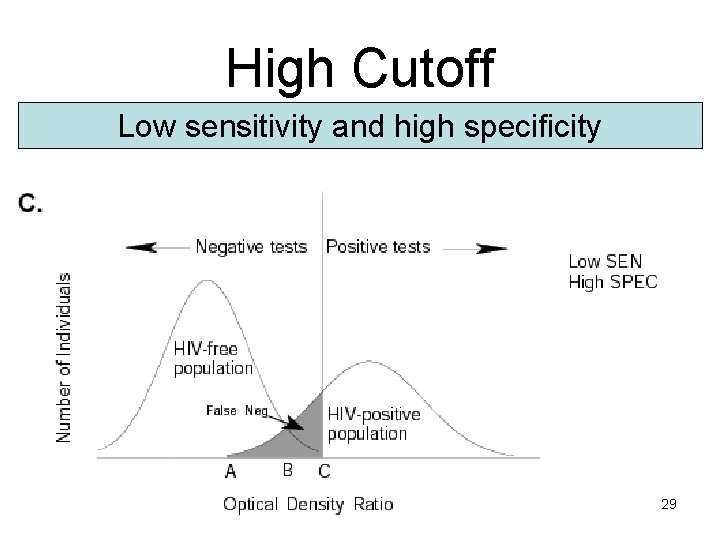
High Cutoff Low sensitivity and high specificity 29

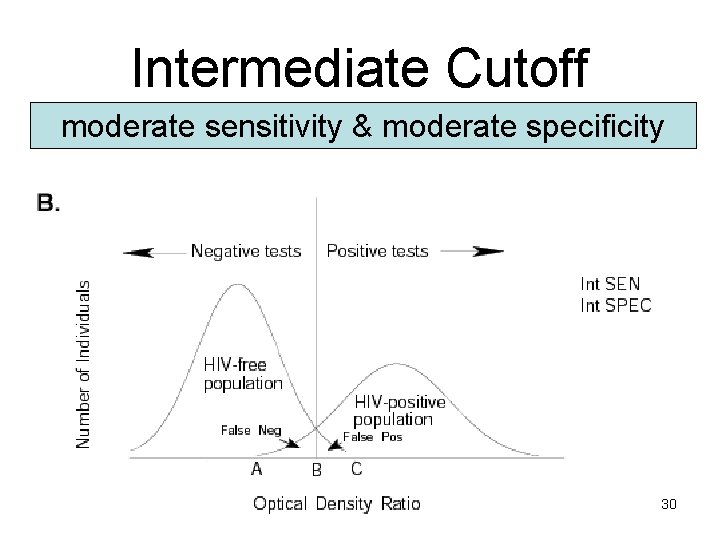
Intermediate Cutoff moderate sensitivity & moderate specificity 30