Chapter 10 Sampling Distributions Essential Statistics Chapter 10

Chapter 10 Sampling Distributions Essential Statistics Chapter 10 1

Population and Sample Researchers often want to answer questions about some large group of individuals, this group is called the population u Often the researchers cannot measure all individuals in the population, so they collect and measure a sample. u The researchers then use statistical techniques to make conclusions about the population based on the sample u Essential Statistics Chapter 7 2

Parameter vs. Statistic u. The mean of a population is denoted by µ – a parameter. u. The mean of a sample is denoted by statistic. is used to estimate µ. Essential Statistics Chapter 10 –a 3

Connection Between Sample Mean & Population Mean Population data: millions of test score Essential Statistics Chapter 10 Sample: N=100 4

Connection Between Sample Mean & population Mean ◙ Why sample mean to be trusted to get population mean? ◙ Sample means vary around the population mean ◙ They don’t vary much and not far from the population mean Essential Statistics Chapter 10 5

The Law of Large Numbers Consider sampling at random from a population with true mean µ. As the number of (independent) observations sampled increases, the mean of the sample gets closer and closer to the true mean of the population. ( gets closer to µ ) Essential Statistics Chapter 10 6

Distribution of Sampling Means u The sampling distribution of is the distribution of values taken by the in all possible samples of the same size (n) from the same population – to describe a distribution we need to specify the shape, center, and spread – we will discuss the distribution of the sample means (x-bar) Essential Statistics Chapter 10 7

Case Study Does This Wine Smell Bad? Dimethyl sulfide (DMS) is sometimes present in wine, causing “off-odors”. Winemakers want to know the odor threshold – the lowest concentration of DMS that the human nose can detect. Different people have different thresholds, and of interest is the mean threshold in the population of all adults. Essential Statistics Chapter 10 8

Case Study Does This Wine Smell Bad? Suppose the mean threshold of all adults is =25 micrograms of DMS per liter of wine, with a standard deviation of =7 micrograms per liter and the threshold values follow a bell-shaped (normal) curve. Essential Statistics Chapter 10 9

Sampling Distribution u What about the mean (average) of a sample of n adults? What values would be expected? u Answer this by thinking: “What would happen if we took many samples of n subjects from this population? ” (let’s say that n=10 subjects make up a sample) – take a large number of samples of n=10 subjects from the population – calculate the sample mean (x-bar) for each sample – make a histogram of the values of x-bar – examine the graphical display for shape, center, spread Essential Statistics Chapter 10 10

Case Study Does This Wine Smell Bad? Mean threshold of all adults is =25 micrograms per liter, with a standard deviation of =7 micrograms per liter and the threshold values follow a bell-shaped (normal) curve. Many (1000) repetitions of sampling n=10 adults from the population were simulated and the resulting histogram of the 1000 x-bar values is on the next slide. Essential Statistics Chapter 10 11

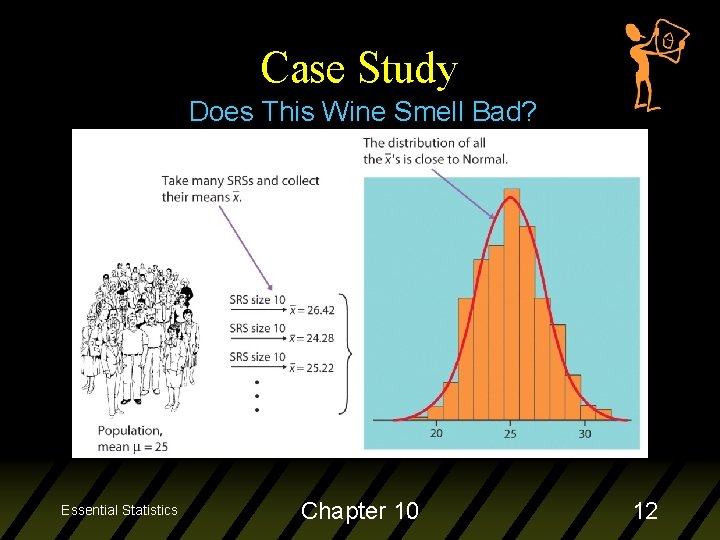
Case Study Does This Wine Smell Bad? Essential Statistics Chapter 10 12

Mean and Standard Deviation of Sample Means If numerous samples of size n are taken from a population with mean m and standard deviation , then the mean of the sampling distribution of is m (the population mean) and the standard deviation is: ( is the population s. d. ) Essential Statistics Chapter 10 13

Connection Between Sample Mean & Population Mean X refer the population distribution refer the sampling distribution of the mean Essential Statistics Chapter 10 14

Mean and Standard Deviation of Sample Means u. Since the mean of is m, we say that is an unbiased estimator of m u. Individual observations have standard deviation , but sample means from samples of size n have standard deviation. Averages are less variable than individual observations. Essential Statistics Chapter 10 15

Sampling Distribution of Sample Means If individual observations have the N(µ, ) distribution, then the sample mean of n independent observations has the N(µ, / distribution. ) “If measurements in the population follow a Normal distribution, then so does the sample mean. ” Essential Statistics Chapter 10 16

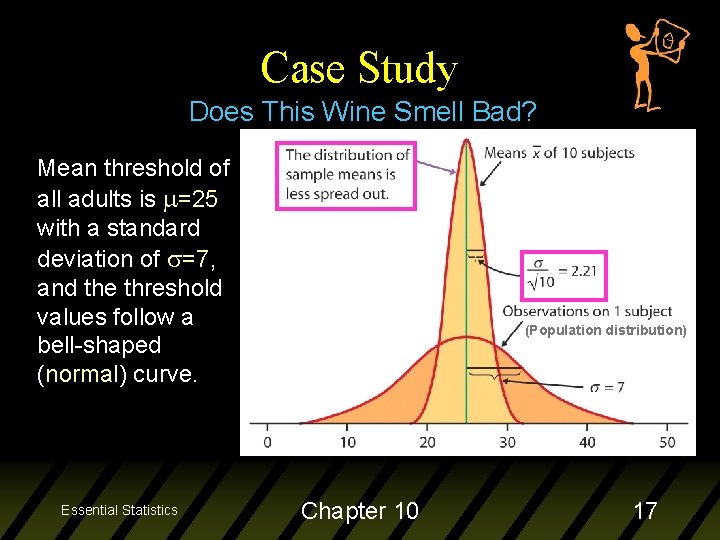
Case Study Does This Wine Smell Bad? Mean threshold of all adults is =25 with a standard deviation of =7, and the threshold values follow a bell-shaped (normal) curve. Essential Statistics (Population distribution) Chapter 10 17

Central Limit Theorem If a random sample of size n is selected from ANY population with mean m and standard deviation , then when n is large the distribution of the sample mean is approximately Normal: is approximately N(µ, / ) “No matter what distribution the population values follow, the sample mean will follow a Normal distribution if the sample size is large. ” Essential Statistics Chapter 10 18

Central Limit Theorem: Sample Size u How large must n be for the CLT to hold? – depends on how far the population distribution is from Normal v the further from Normal, the larger the sample size needed v a sample size of 25 or 30 is typically large enough for any population distribution encountered in practice v recall: if the population is Normal, any sample size will work (n≥ 1) Essential Statistics Chapter 10 19

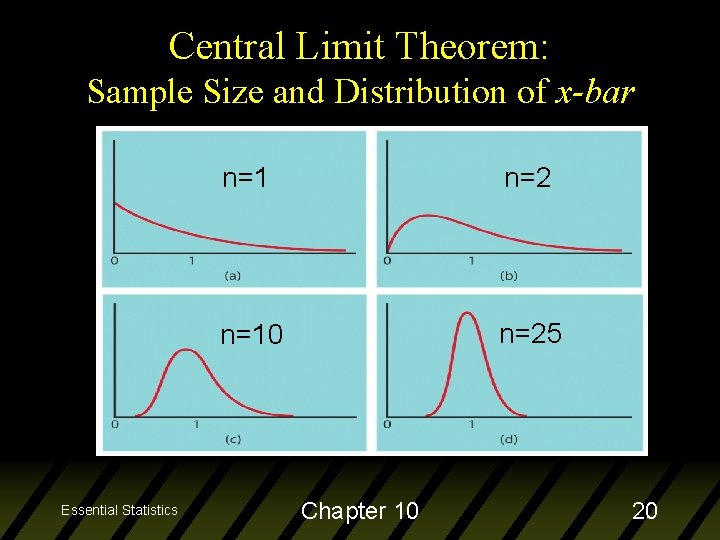
Central Limit Theorem: Sample Size and Distribution of x-bar Essential Statistics n=1 n=2 n=10 n=25 Chapter 10 20

Chapter 10 home work guide down population distribution N (µ, ). u Write down sample means (x-bar) distribution N (µ, / ), n – sample size. u When n=1, individual observation, using calculate z–score u When n > 1, sample means ( ) observation, using / calculate z-score. The z value will increased and the corresponding probability will change too. u Write Essential Statistics Chapter 10 21

Video Reference http: //www. youtube. com/watch? v=Lfg. Pm. KTd. Us. E http: //www. onlinemathlearning. com/sampling-distribution. html Essential Statistics Chapter 10 22