Chapter 10 Rotation of a rigid object about

Chapter 10: Rotation of a rigid object about a fixed axis Part 2 Reading assignment: Chapter 11. 1 -11. 3 Homework : (due Wednesday, Oct. 12, 2005): Problems: Q 4, 2, 5, 18, 21, 23, 24, • Rotational motion, • Angular displacement, angular velocity, angular acceleration • Rotational energy • Moment of Inertia (Rotational inertia) • Torque • For every rotational quantity, there is a linear analog.

Black board example 11. 3 HW 27 (a) What is the angular speed w about the polar axis of a point on Earth’s surface at a latitude of 40°N (b) What is the linear speed v of that point? (c) What are w and v for a point on the equator? Radius of earth: 6370 km

Rotational energy A rotating object (collection of i points with mass mi) has a rotational ______ energy of Where: Rotational inertia

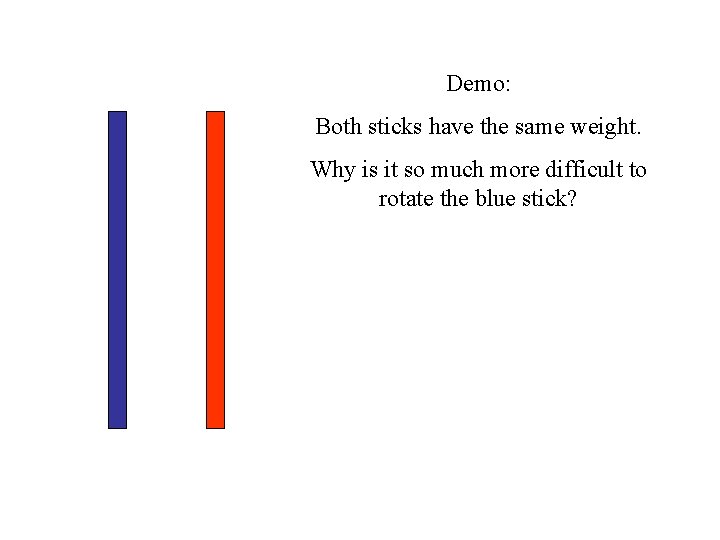
Demo: Both sticks have the same weight. Why is it so much more difficult to rotate the blue stick?

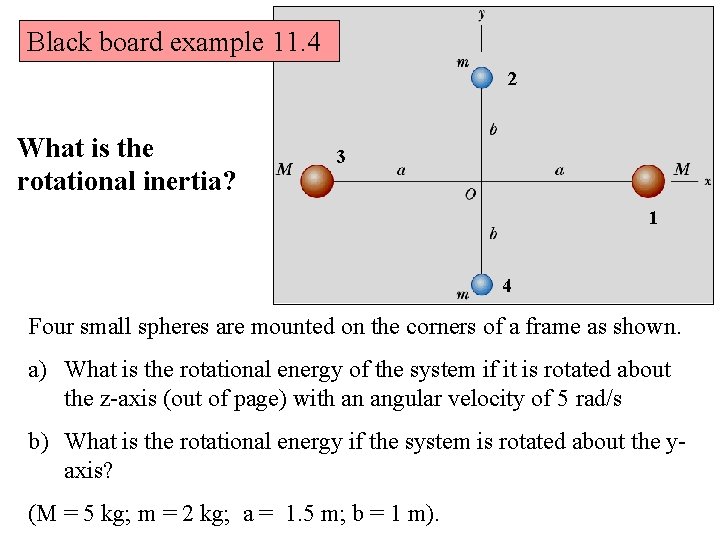
Black board example 11. 4 2 What is the rotational inertia? 3 1 4 Four small spheres are mounted on the corners of a frame as shown. a) What is the rotational energy of the system if it is rotated about the z-axis (out of page) with an angular velocity of 5 rad/s b) What is the rotational energy if the system is rotated about the yaxis? (M = 5 kg; m = 2 kg; a = 1. 5 m; b = 1 m).

Rotational inertia of an object depends on: - the ____ about which the object is rotated. - the _____ of the object. - the _____ between the mass(es) and the axis of rotation.

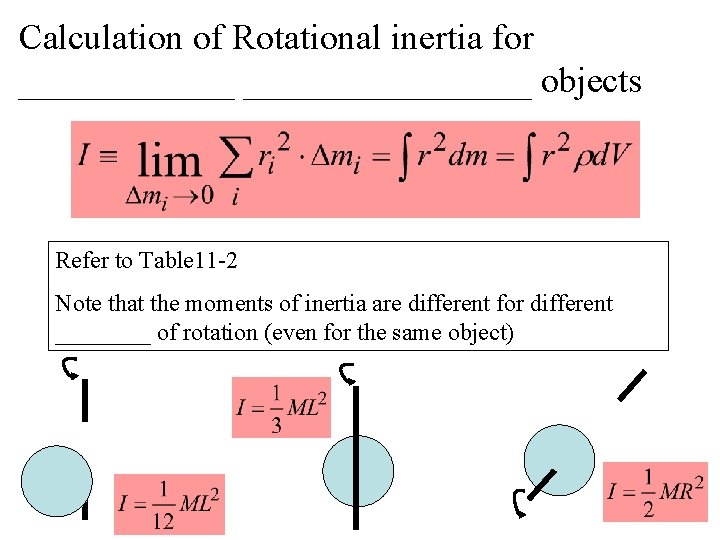
Calculation of Rotational inertia for ________________ objects Refer to Table 11 -2 Note that the moments of inertia are different for different ____ of rotation (even for the same object)

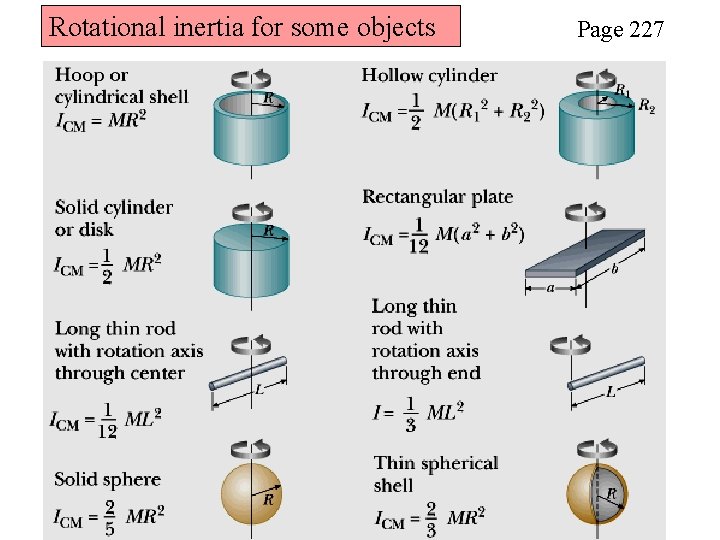
Rotational inertia for some objects Page 227

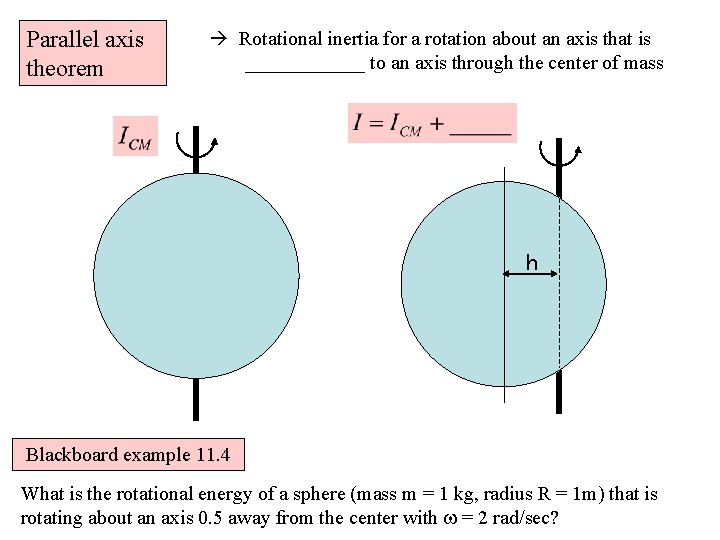
Parallel axis theorem Rotational inertia for a rotation about an axis that is ______ to an axis through the center of mass h Blackboard example 11. 4 What is the rotational energy of a sphere (mass m = 1 kg, radius R = 1 m) that is rotating about an axis 0. 5 away from the center with w = 2 rad/sec?

Conservation of energy (including rotational energy): Again: If there are no __________ forces: Energy is conserved. Rotational _______ energy must be included in energy considerations!

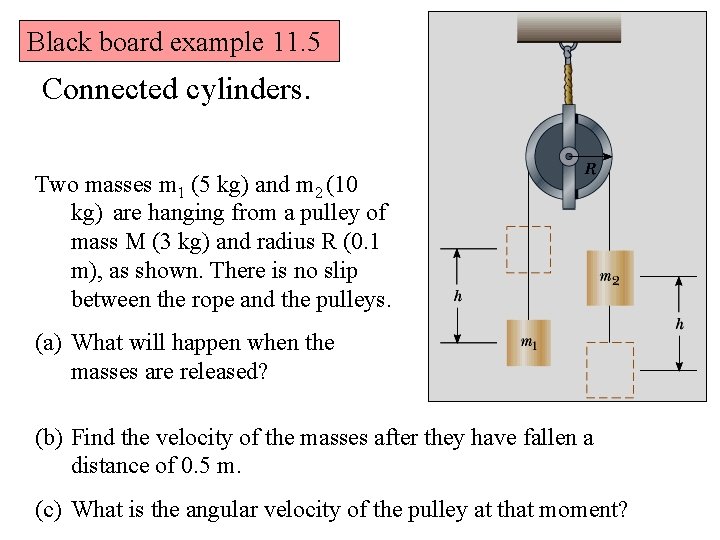
Black board example 11. 5 Connected cylinders. Two masses m 1 (5 kg) and m 2 (10 kg) are hanging from a pulley of mass M (3 kg) and radius R (0. 1 m), as shown. There is no slip between the rope and the pulleys. (a) What will happen when the masses are released? (b) Find the velocity of the masses after they have fallen a distance of 0. 5 m. (c) What is the angular velocity of the pulley at that moment?

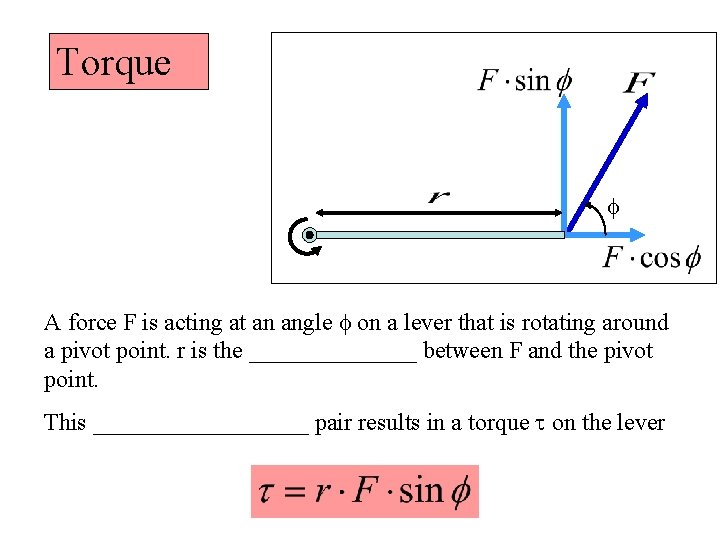
Torque f A force F is acting at an angle f on a lever that is rotating around a pivot point. r is the _______ between F and the pivot point. This _________ pair results in a torque t on the lever

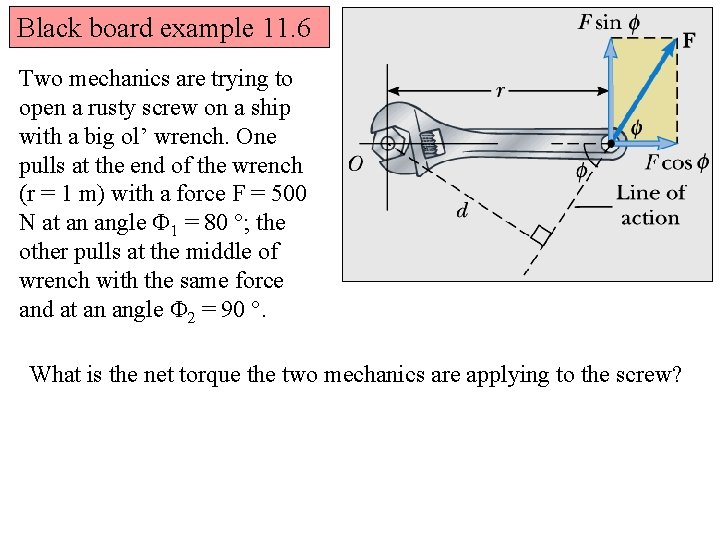
Black board example 11. 6 Two mechanics are trying to open a rusty screw on a ship with a big ol’ wrench. One pulls at the end of the wrench (r = 1 m) with a force F = 500 N at an angle F 1 = 80 °; the other pulls at the middle of wrench with the same force and at an angle F 2 = 90 °. What is the net torque the two mechanics are applying to the screw?

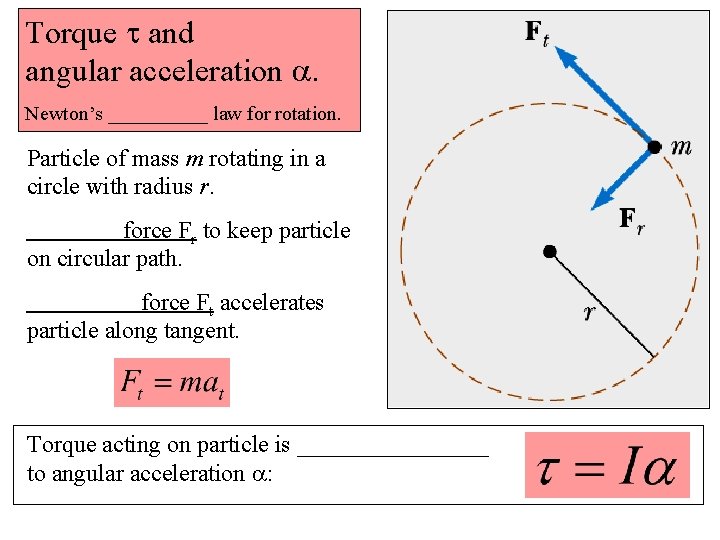
Torque t and angular acceleration a. Newton’s _____ law for rotation. Particle of mass m rotating in a circle with radius r. force Fr to keep particle on circular path. force Ft accelerates particle along tangent. Torque acting on particle is ________ to angular acceleration a:

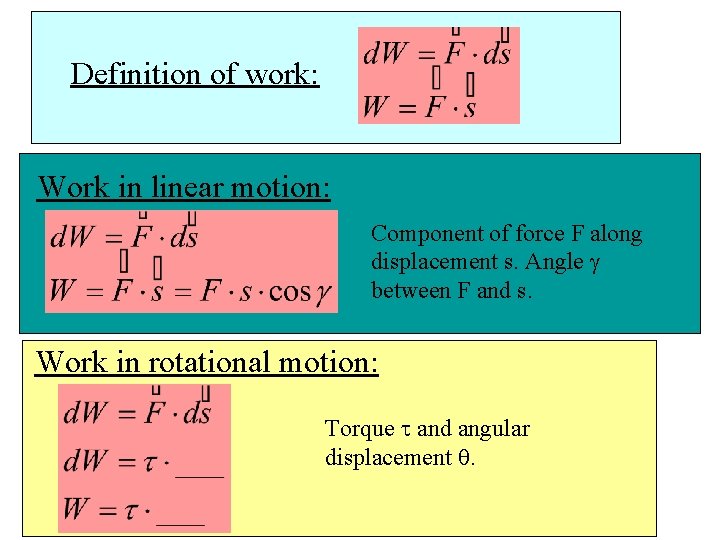
Definition of work: Work in linear motion: Component of force F along displacement s. Angle g between F and s. Work in rotational motion: Torque t and angular displacement q.

Work and Energy in rotational motion Remember work-kinetic energy theorem for linear motion: External work done on an object changes its _____ energy There is an equivalent work-rotational kinetic energy theorem: External, rotational work done on an object changes its ________energy

Linear motion with constant linear acceleration, a. Rotational motion with constant rotational acceleration, a.

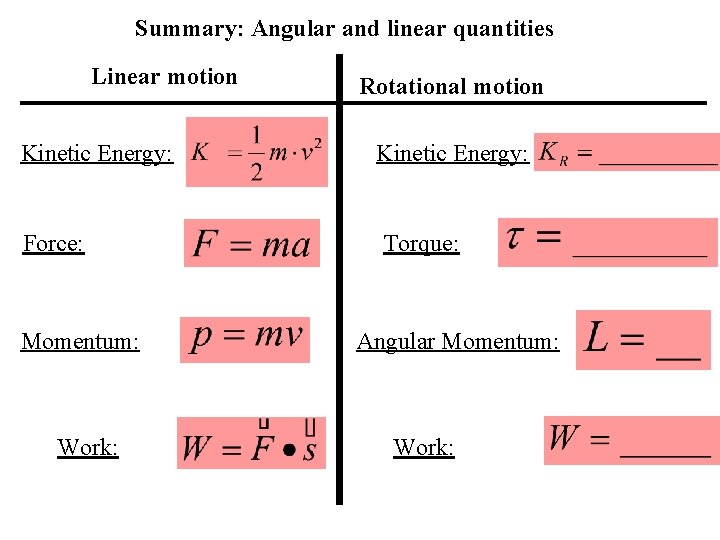
Summary: Angular and linear quantities Linear motion Rotational motion Kinetic Energy: Force: Torque: Momentum: Work: Angular Momentum: Work: