Chapter 10 Resource Allocation Linear Integer Programming Chapter

Chapter 10. Resource Allocation Linear & Integer Programming Chapter 10: Quantitatve Methods in Health Care Management Yasar A. Ozcan 1

Outline u Linear Programming – – – u u u Concept Structure of Linear Programming Model Formulation Graphical Conceptualization Computer Based Solutions Interpretation of Results Maximization Models Minimization Models Integer Programming – Staff scheduling Chapter 10: Quantitatve Methods in Health Care Management Yasar A. Ozcan 2

The Concept Linear Programming (LP) models are excellent tools to solve allocation, purchasemix, scheduling problems, etc. A large number of decision variables can be incorporated into a single model to attain an optimal solution to a problem. Chapter 10: Quantitatve Methods in Health Care Management Yasar A. Ozcan 3

Structure of an LP model The structure contains four components: Objective-- either maximization or minimization; a mathematical statement of profit, cost, etc. per unit of output or input. Decision Variables-- amount of either inputs or outputs. Constraints-alternatives. limitations that restrict the available Parameters-- numerical values (e. g. , values of available resources). Chapter 10: Quantitatve Methods in Health Care Management Yasar A. Ozcan 4

Structure of an LP model General structure of the linear programming model is as follows: Maximize (or minimize) Z = c 1 x 1 + c 2 x 2 + c 3 x 3 + ……+ cnxn Subject to: a 11 x 1 + a 12 x 2 + a 13 x 3 + ……+ a 1 nxn (≤, =, ≥ ) b 1 a 21 x 1 + a 22 x 2 + a 23 x 3 + ……+ a 2 nxn (≤, =, ≥ ) b 2 a 31 x 1 + a 32 x 2 + a 33 x 3 + ……+ a 3 nxn (≤, =, ≥ ) b 3. . am 1 x 1+ am 2 x 2+am 3 x 3+ ……+amnxn (≤, =, ≥ ) bm xi ≥ 0. where Z = objective function xi = decision variables bj = available resource for jth constraint ci = objective function coefficients aij= coefficient for ith decision variable on jth constraint. Chapter 10: Quantitatve Methods in Health Care Management Yasar A. Ozcan 5

Maximization Models Maximization models seek either revenue or profit maximization. To illustrate these concepts in an example and build a linear programming model for it, consider the following maximization example. Chapter 10: Quantitatve Methods in Health Care Management Yasar A. Ozcan 6

Example 10. 1 An insurance company desires to enter the healthcare market and offer its potential customers both a staff model Health Maintenance Organization (HMO) and commercial indemnity insurance. The company is in deciding how to allocate its marketing efforts between those options to maximize its profits. The analysts have estimated that the company will realize a profit of $1, 200 per enrollee from the HMO, and $600 per enrollee from commercial plans. Furthermore, for the coming year the company is forced to rely on its present resources in terms of sales force. The administrative support of the HMO will take 200 hours, and the commercial administration will take, on average, 400 hours; currently, the company can allocate 1. 6 million hours to sales. To break even, the HMO requires that the contribution margins (contribution margin is sales revenue less variable costs; it is the amount available to pay for fixed costs and then provide any profit after variable costs have been paid) for enrollees must exceed $1. 5 million. The estimated contribution margins are $500 and $300, for HMO and for commercial insurances enrollees, respectively. With a limited number of physicians participating in the staff model HMO at the present time, the HMO can handle at most 5, 000 enrollees. Chapter 10: Quantitatve Methods in Health Care Management Yasar A. Ozcan 7

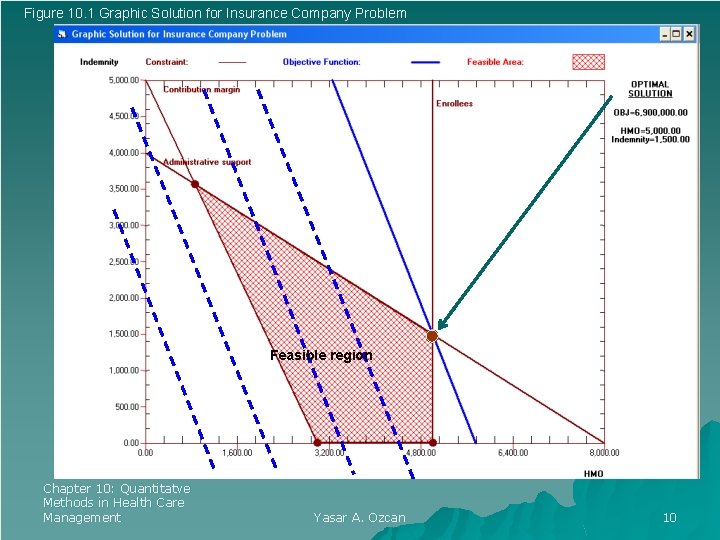
Solution: To formulate the model for this problem, first we must identify the decision variables. In this case the two options, HMO and indemnity insurance, are the decision variables. The number of enrollees required for profitable operations is determined by the level of activity in each of those variables. Let us assign a symbol of x 1 to indicate the potential number of HMO enrollees; similarly let x 2 represent the enrollees in the indemnity plan. The next step is to express the objective function in a linear fashion to represent the maximum profits for each of those decision variables. Recall that the company was expecting, respectively, $1, 200 and $600 profit from each HMO and each indemnity enrollee. The objective function is the summation of these expectations and can be formulated as: Maximize Z (profit) = 1, 200 x 1 +600 x 2. Chapter 10: Quantitatve Methods in Health Care Management Yasar A. Ozcan 8

Maximize Z (profit) = 1, 200 x 1 +600 x 2. Subject to: 200 x 1 + 400 x 2 ≤ 1, 600, 000 (administrative support constraint) 500 x 1 + 300 x 2 ≥ 1, 500, 000 (contribution margin constraint) 1 x 1 + 0 x 2 ≤ 5, 000 (enrollees constraint) x 1, x 2 ≥ 0 (non-negativity constraint) Chapter 10: Quantitatve Methods in Health Care Management Yasar A. Ozcan 9

Figure 10. 1 Graphic Solution for Insurance Company Problem Feasible region Chapter 10: Quantitatve Methods in Health Care Management Yasar A. Ozcan 10

Minimization Models When the measures in the objective function are costs, obviously healthcare managers seek to minimize those costs. Model set-up follows the same steps, with one exception: in cost minimization problems, the constraints are generally the ≥ type. Thus, in the graphic solution, the feasible area is defined from infinity towards origin. Chapter 10: Quantitatve Methods in Health Care Management Yasar A. Ozcan 11

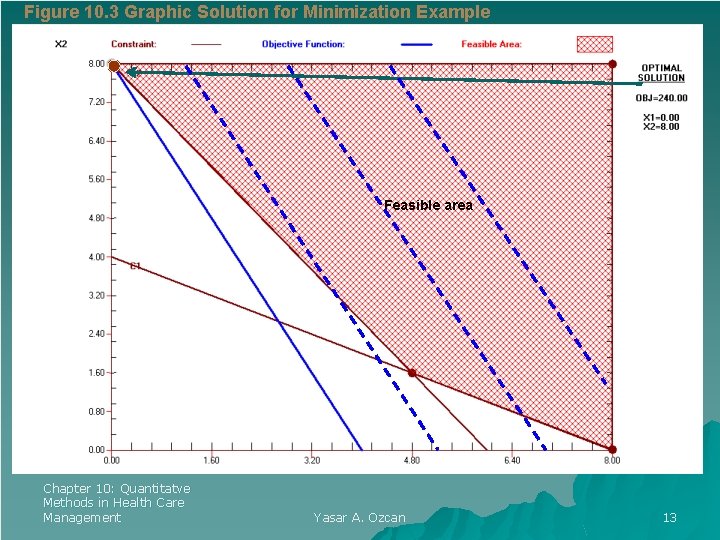
Minimization Models Example 10. 2 Minimize Z = 60 x 1 +30 x 2 Subject to: 20 x 1 + 40 x 2 ≥ 160 40 x 1 + 30 x 2 ≥ 240 x 1, x 2 ≥ 0 Chapter 10: Quantitatve Methods in Health Care Management C 1 (constraint 1) C 2 (constraint 2) Yasar A. Ozcan 12

Figure 10. 3 Graphic Solution for Minimization Example Feasible area Chapter 10: Quantitatve Methods in Health Care Management Yasar A. Ozcan 13

Interpretation of Results Binding Constraint-- A constraint that forms the optimal corner point of the feasible solution space Slack-- When optimal values of decision variables are substituted into a <= constraint, and the resulting value is less than the right hand side value Surplus-- When optimal values of decision variables are substituted into a >= constraint, and the resulting values exceed the right hand side value Shadow Prices-- How much a one-unit increase in the right hand side of a constraint would increase the value of the objective function Range of Feasibility-- Range of values for the right side of a constraint over which the shadow price remains the same. Chapter 10: Quantitatve Methods in Health Care Management Yasar A. Ozcan 14

Integer Linear Programming In linear programming one of the assumptions is that decision variables are continuous. Therefore solutions can yield fractional values such as 4. 3 patients, or 7. 6 nurses. Such solutions are especially impractical, however, when linear programming is used for scheduling the clinical staff. Rounding off these values may generate infeasible or less optimal solutions. Integer programming is an extension of linear programming that eliminates the problem by enforcing integer decision variable outcomes. Chapter 10: Quantitatve Methods in Health Care Management Yasar A. Ozcan 15

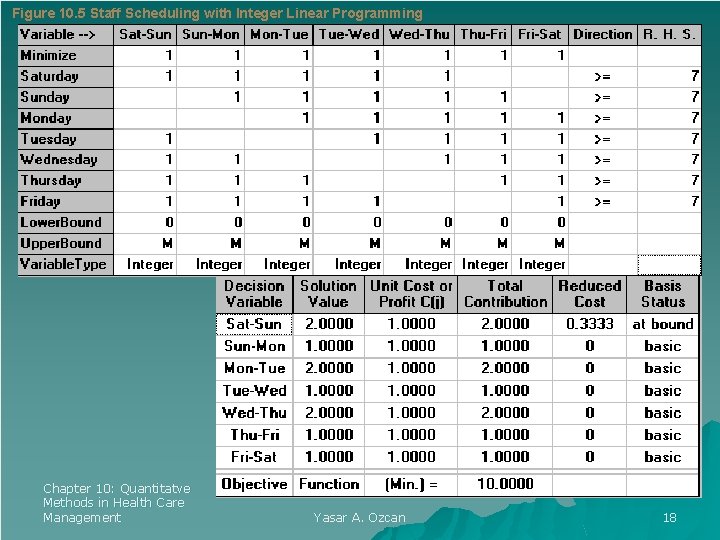
Integer Linear Programming A formal formulation of integer linear programming for staff assignments is as follows (adapted from Fitzsimmons & Fitzsimmons, 2004, p. 255): Minimize) Z = x 1 + x 2 + x 3 + x 4 + x 5 + x 6 Subject to: x 1 + x 2 + x 3 + x 4 + x 5 ≥ b 1 x 2 + x 3 + x 4 + x 5 + x 6 ≥ b 2 x 3 + x 4 + x 5 + x 6 + x 7 ≥ b 3 x 1 + x 4 + x 5 + x 6 + x 7 ≥ b 4 x 1 + x 2 + x 5 + x 6 + x 7 ≥ b 5 x 1 + x 2 + x 3 + x 6 + x 7 ≥ b 6 x 1 + x 2 + x 3 + x 4 + x 7 ≥ b 7 xi ≥ 0 and integer + x 7 Saturday constraint Sunday constraint Monday constraint Tuesday constraint Wednesday constraint Thursday constraint Friday constraint where Z = objective function xi = decision variables (x 1=off on Saturday & Sunday, x 2=off on Sunday & Monday, etc. ) bj = minimum staff requirements for a day of the week (b 1 = required staff for Saturday). Chapter 10: Quantitatve Methods in Health Care Management Yasar A. Ozcan 16

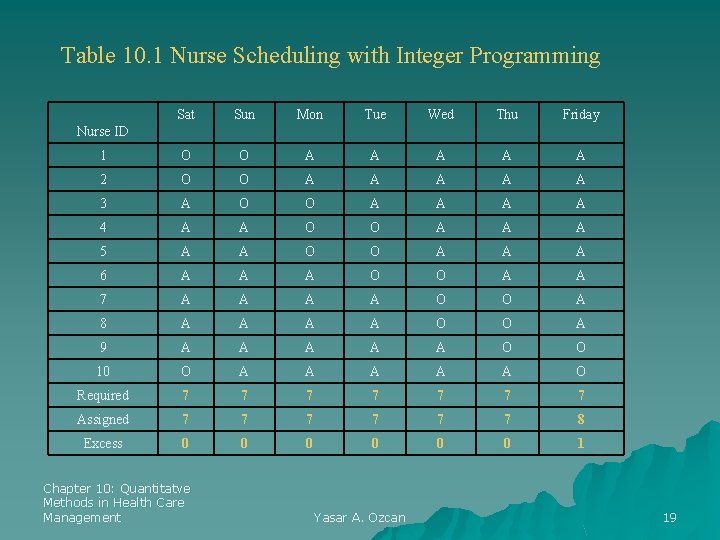
Example 10. 3 A nurse manager must schedule staff nurses in a rehab unit. Nurses work five days a week with two consecutive off days. The staff requirements of the nursing unit are seven nurses for each day of the week. The nurse manager wants an equitable schedule for all the staff while meeting the unit staff requirements each day. Solution: Since this problem has more than two decision variables, a graphic solution is not possible. A computer solution using Win. QSB will be provided. Exhibit 10. 3 displays the data entry and the solution to this problem. Chapter 10: Quantitatve Methods in Health Care Management Yasar A. Ozcan 17

Figure 10. 5 Staff Scheduling with Integer Linear Programming Chapter 10: Quantitatve Methods in Health Care Management Yasar A. Ozcan 18

Table 10. 1 Nurse Scheduling with Integer Programming Sat Sun Mon Tue Wed Thu Friday 1 O O A A A 2 O O A A A 3 A O O A A 4 A A O O A A A 5 A A O O A A A 6 A A A O O A A 7 A A O O A 8 A A O O A 9 A A A O O 10 O A A A O Required 7 7 7 7 Assigned 7 7 7 8 Excess 0 0 0 1 Nurse ID Chapter 10: Quantitatve Methods in Health Care Management Yasar A. Ozcan 19

The End Chapter 10: Quantitatve Methods in Health Care Management Yasar A. Ozcan 20