Chapter 10 Quantitative Facilities Planning Models Presented by

Chapter # 10 Quantitative Facilities Planning Models Presented by: Inamullah Arif Ali Group 10 11 -IE-55 11 -IE-56 Muhammad Badar 11 -IE-65

Overview v Facility Location Model: v Rectilinear Distance Facility Location: v Single Facility Rectilinear Minisum: v Euclidean Facility Location: v Single Facility Squared Euclidean Minisum:

Facility Location Model v The ”facility location Model”, also known as location analysis, is a branch of operations research and computational geometry concerned with the “optimal placement of facilities” to minimize transportation costs. v The techniques also apply to cluster analysis

Facility Location Problems can be classified: v Number of new facilities to be located v The solution space v The size of facilities v The criteria used to determine the location v. The distance measured

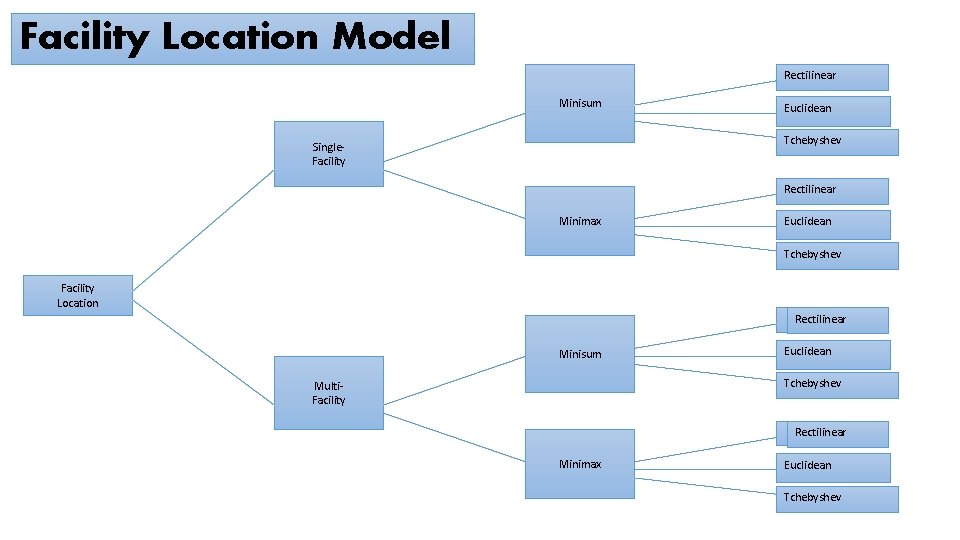
Facility Location Model Rectilinear Minisum Euclidean Tchebyshev Single. Facility Rectilinear Minimax Euclidean Tchebyshev Facility Location Rectilinear Minisum Euclidean Tchebyshev Multi. Facility Rectilinear Minimax Euclidean Tchebyshev

Analytical Methods of Location Planning Ø The various analytical methods of location planning are affected by the way the “distances are measured”. Ø Distance measure: § A mathematical model used to evaluate flexible-flow layouts based on proximity factors. § There are two ways to measure the distance between two facilities. Ø Rectilinear Distance Ø Euclidean Distance

Rectilinear Distance Facility Location Ø Rectilinear distance • When distance between two facilities is measured along path that is “orthogonal (90 degree)” to each other, then that distance is termed as rectilinear distance. Suppose two facilities are located at points represented by (X 1, Y 1) and at (X 2, Y 2) then the rectilinear distance between the facilities will be : Ø |X 1 -X 2|+|Y 1 -Y 2|

Applications of Rectilinear Distance ØRectilinear Distance facility location problem because it represents a situation commonly encountered in manufacturing and distribution settings. ØIt occurs in many cities, due to the layout streets. Ø An industrial example is a material transporter moving along Rectilinear aisles in a factory

Single Facility Rectilinear Minisum ØThe annual cost of travel B/W the new facility and existing facility is assumed to be proportional to the distance B/W the points X and Pi, with wi denoting the constant of proportionality. ØThe objective is to;

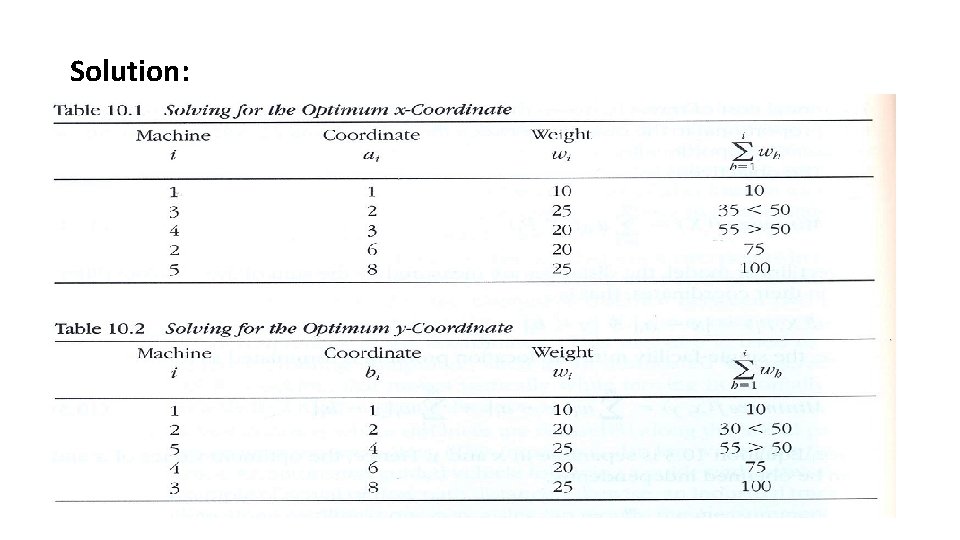
Solution:

Euclidean Distance Facility Location: q Euclidean distance: Ø “Shortest distance between two points” Ø When distance is measured “along straight-line path” between the two facilities, then that distance is termed as “Euclidean distance”. Ø {( X 1 - X 2 )^2 + ( Y 1 - Y 2 )^2}1/2

Applications of Euclidean Distance Facility location: v There are situations in which Euclidean distance is an accurate representation of the location problem being studied ü For examples: Ø Locating cell phone towers to provide coverage, Ø Determine where to locate sniper (shoot bullets in a straight line) Can be modeled accurately using “Euclidean Distances”. Ø In industrial setting “Conveyors” and “pneumatic tubes” often follow straight line paths (Euclidean distance).

Single Facility Squared Euclidean Minisum Ø Squared Euclidean Minisum often referred to as the “gravity problem”. ØIn this the “COST OF TRAVEL” between a single new facility and multiple existing facilities to be proportional to the square of the Euclidean distance between the facilities ØThe optimum solution for the gravity problem is “centroid location”

The gravity (Euclidean) problem can be formulated as: Ø Min. f(x , y) = Wi[ (x-a)2 +(y-b)2] Ø Taking partial derivate w. r. t X & Y, & setting them equal to zero X* = X *W Wi i = x, y = i YW Wi i* Y* where, coordinates of the new facility xi, yi = coordinates of existing facility i W i = annual weight shipped from facility i

Solution: Using this formula

THANK YOU!!