Chapter 10 Quantitative Data Analysis Chapter Objectives Understand

Chapter 10 – Quantitative Data Analysis

Chapter Objectives Understand differences in measurement scale ○ How to code measurements on the spread sheet Understand different analysis methods for different scales Understand how to read and interpret results Develop your own research with appropriate analysis method

Scales

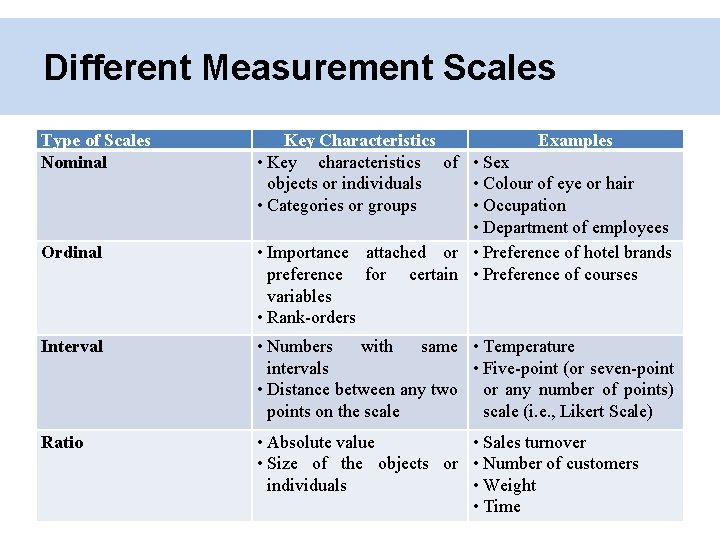
Different Measurement Scales Type of Scales Nominal Ordinal Key Characteristics Examples • Key characteristics of • Sex objects or individuals • Colour of eye or hair • Categories or groups • Occupation • Department of employees • Importance attached or • Preference of hotel brands preference for certain • Preference of courses variables • Rank-orders Interval • Numbers with same • Temperature intervals • Five-point (or seven-point • Distance between any two or any number of points) points on the scale (i. e. , Likert Scale) Ratio • Absolute value • Sales turnover • Size of the objects or • Number of customers individuals • Weight • Time

Nominal Scale Nominal ○ Categories or groups ○ Gender, occupation, department of employees in an organization What was the type of restaurant that you have dined most recently? Fast food restaurant Casual dining restaurant Upscale restaurant

Ordinal Scale Ordinal ○ Rank orders the categories ○ An individual’s preference of hotel brands (rank) ○ A hospitality student’s preference of courses (rank) Service Quality Dimensions 1. Tangibles 2. Reliability 3. Responsiveness 4. Assurance 5. Empathy Ranking of Importance ________ ____

Interval Scale ○ Numbers with same intervals • Distance from 1 to 2 is same as the distance from 2 to 3 ○ Measure the distance between any two points on the scale Likert Scale ○ A psychometric scale commonly used in research that employs questionnaires ○ The most widely used approach to scaling in survey research, such that the term is often used interchangeably rating scale ○ It is a statement which the respondent is asked to evaluate according to any kind of subjective or objective criteria • The level of agreement or disagreement is measured

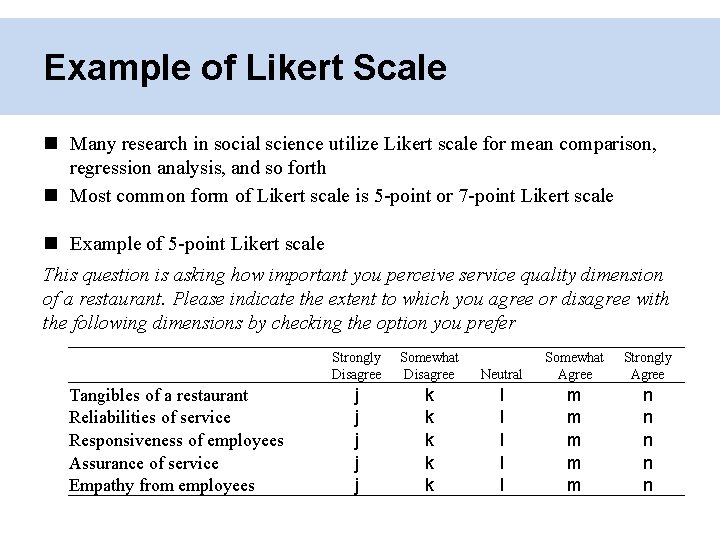
Example of Likert Scale Many research in social science utilize Likert scale for mean comparison, regression analysis, and so forth Most common form of Likert scale is 5 -point or 7 -point Likert scale Example of 5 -point Likert scale This question is asking how important you perceive service quality dimension of a restaurant. Please indicate the extent to which you agree or disagree with the following dimensions by checking the option you prefer Tangibles of a restaurant Reliabilities of service Responsiveness of employees Assurance of service Empathy from employees Strongly Disagree Somewhat Disagree j j j k k k Neutral Somewhat Agree Strongly Agree l l l m m m n n n

Ratio Scale ○ Has unique ‘zero’ origin ○ Multiplication & division 1 a. What was the sales turnover for the start-up year? 1 b. What is the sales turnover for 2006? 2 a. How many people did you employ in the start-up year? 2 c. How many people do/did you employ in 2006? £_______________

Coding / Entering Data for Analysis Variable ○ An indicator of interest in a research ○ May take any of a specified set of values, perceptions, attitudes, and attributes Measurement What was the type of restaurant that you have dined most recently? Fast food restaurant Casual dining restaurant Upscale restaurant

Entering Data What was the type of restaurant that you have dined most recently? Fast food restaurant Casual dining restaurant Upscale restaurant

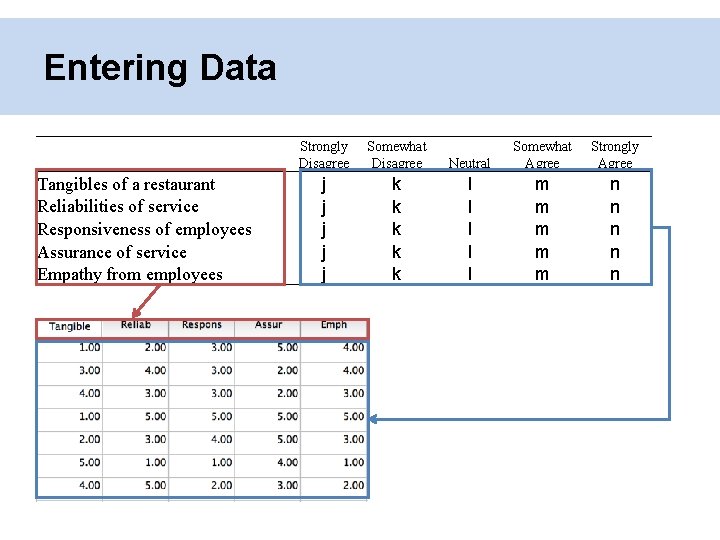
Entering Data Tangibles of a restaurant Reliabilities of service Responsiveness of employees Assurance of service Empathy from employees Strongly Disagree Somewhat Disagree j j j k k k Neutral Somewhat Agree Strongly Agree l l l m m m n n n

Analysing Quantitative Data

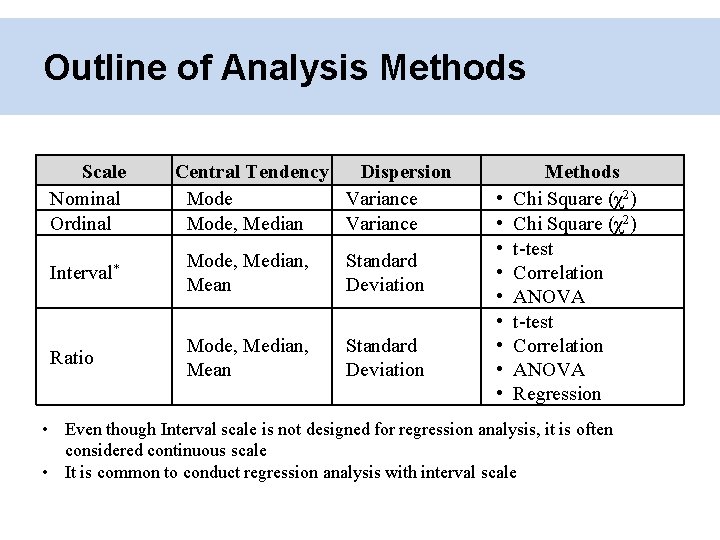
Outline of Analysis Methods Scale Nominal Ordinal Central Tendency Dispersion Mode Variance Mode, Median Variance Interval* Mode, Median, Mean Standard Deviation Ratio Mode, Median, Mean Standard Deviation • • • Methods Chi Square (χ2) t-test Correlation ANOVA Regression • Even though Interval scale is not designed for regression analysis, it is often considered continuous scale • It is common to conduct regression analysis with interval scale

Descriptive Statistics #1 Mean ○ Sum of all values divided by their number ○ Standard Deviation ○ The amount of variation or dispersion from the average (mean) ○

Descriptive Statistics #2 Median ○ Middle piece of data ○ 1, 2, 2, 2, 3, 3, 4, 4, 5, 6, 6, 6, 6. ○ Median = 4 Mode ○ Most frequently observed value in the dataset ○ 4, 6, 1, 2, 6, 3, 4, 5, 2, 6, 6, 3, 3, 3, 6, 4, 2, 6 ○ Mode = 6

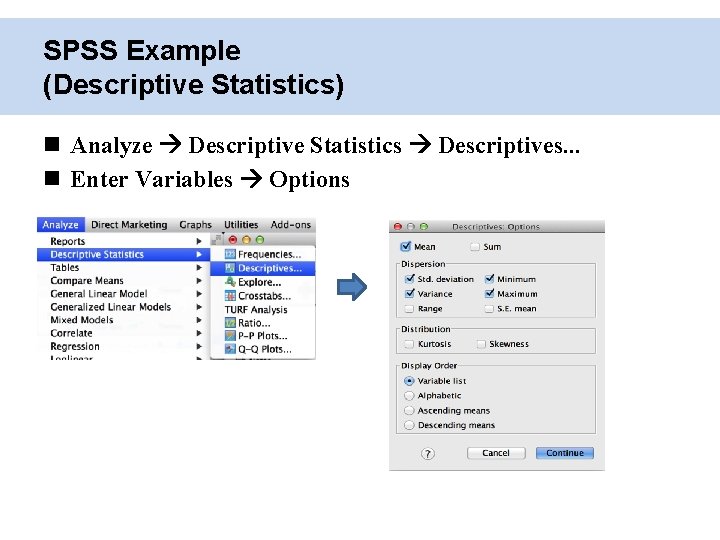
SPSS Example (Descriptive Statistics) Analyze Descriptive Statistics Descriptives. . . Enter Variables Options

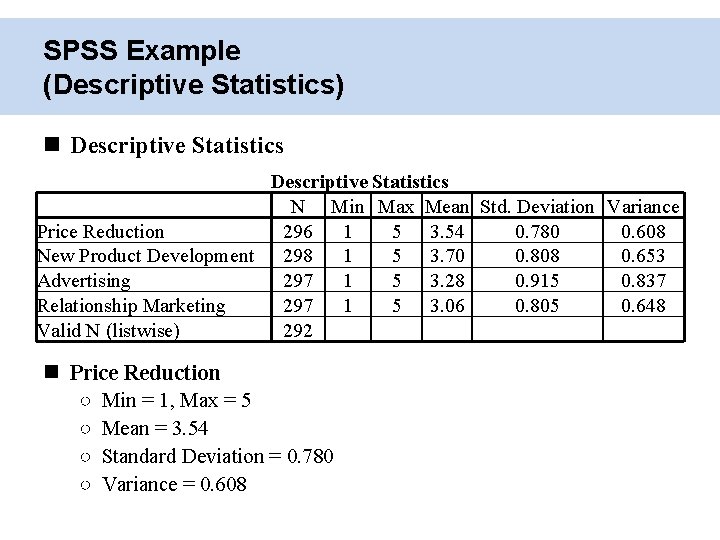
SPSS Example (Descriptive Statistics) Descriptive Statistics N Min Max Mean Std. Deviation Variance Price Reduction 296 1 5 3. 54 0. 780 0. 608 New Product Development 298 1 5 3. 70 0. 808 0. 653 Advertising 297 1 5 3. 28 0. 915 0. 837 Relationship Marketing 297 1 5 3. 06 0. 805 0. 648 Valid N (listwise) 292 Price Reduction ○ Min = 1, Max = 5 ○ Mean = 3. 54 ○ Standard Deviation = 0. 780 ○ Variance = 0. 608

SPSS Example (Frequencies) Analyse Descriptive Statistics Frequencies Statistics or Charts

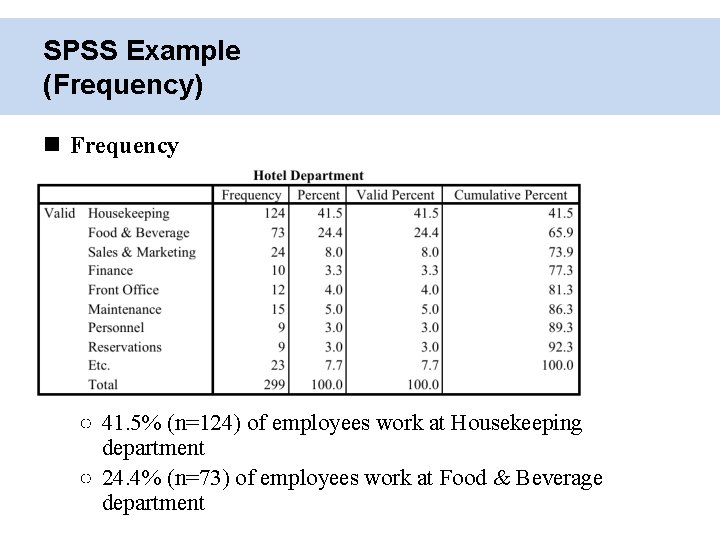
SPSS Example (Frequency) Frequency ○ 41. 5% (n=124) of employees work at Housekeeping department ○ 24. 4% (n=73) of employees work at Food & Beverage department

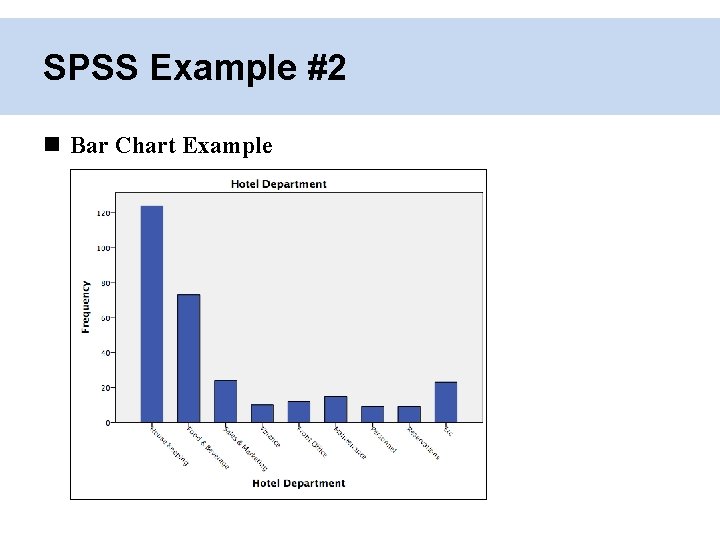
SPSS Example #2 Bar Chart Example

Exploring Relationships between Variables b. Relationships

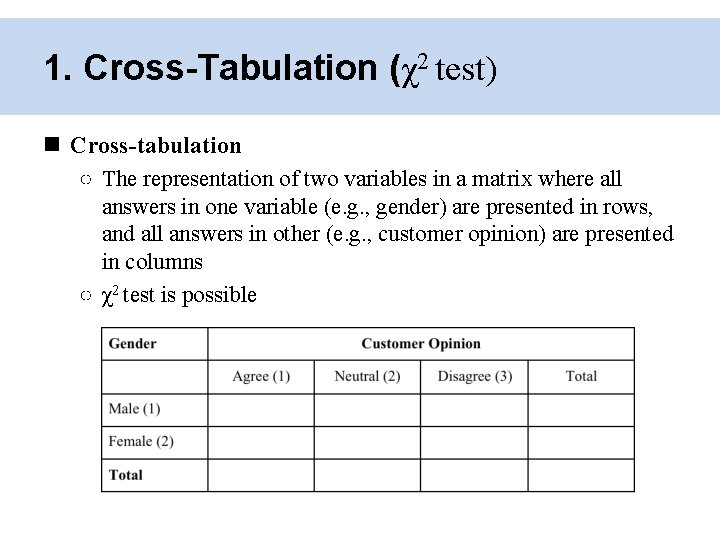
1. Cross-Tabulation (χ2 test) Cross-tabulation ○ The representation of two variables in a matrix where all answers in one variable (e. g. , gender) are presented in rows, and all answers in other (e. g. , customer opinion) are presented in columns ○ χ2 test is possible

SPSS Example (Cross-Tabulation) Hypothesis ○ H 0: Employment status (part-time vs. full-time) does not differ according to the hotel brand scale Analyze Descriptive Statistics Crosstabs… Statistics Select Chi-square

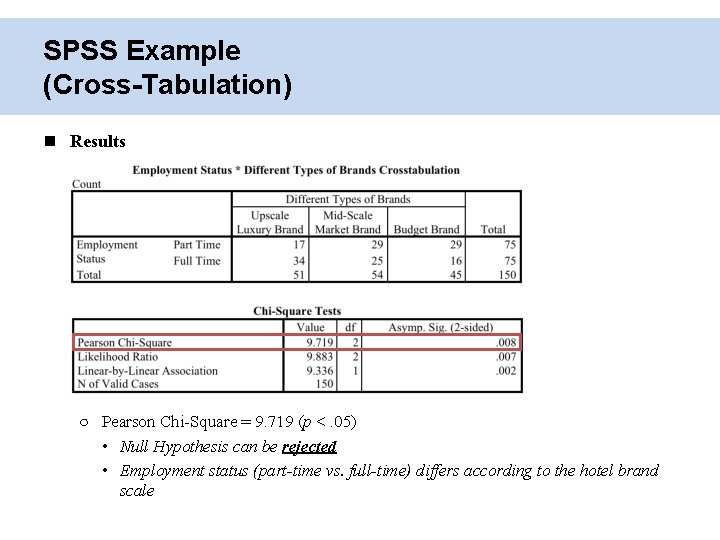
SPSS Example (Cross-Tabulation) Results ○ Pearson Chi-Square = 9. 719 (p <. 05) • Null Hypothesis can be rejected • Employment status (part-time vs. full-time) differs according to the hotel brand scale

2. Correlation Pearson Correlation ○ The degree to which a change in a variable is related to a change in one or more other variable(s) ○ Identify the strength of relationship ○ Cannot tell the causal relationship One-tailed vs. Two-tailed ○ Specific direction is hypothesized One-tailed ○ Non-directional hypotheses Two-tailed

SPSS Example (Correlation) Hypothesis ○ H 1: Service performance is negatively related to service performance but positively correlated to time spent training Analyze Correlate Bivariate… Option Pearson Correlation Coefficient

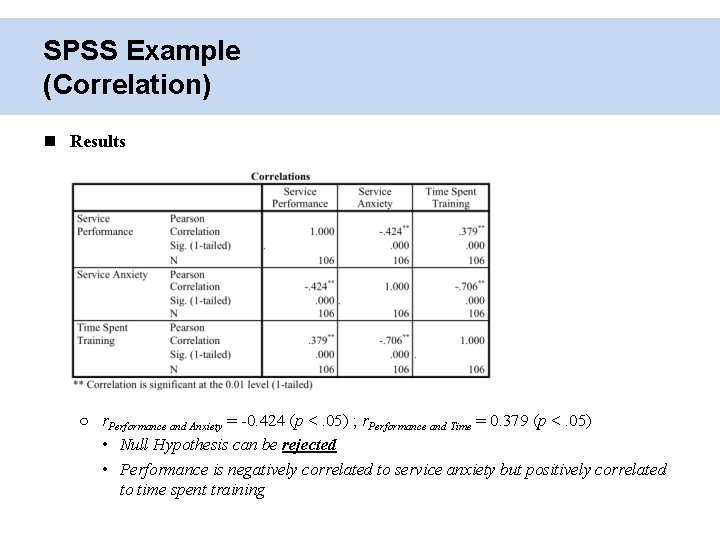
SPSS Example (Correlation) Results ○ r. Performance and Anxiety = -0. 424 (p <. 05) ; r. Performance and Time = 0. 379 (p <. 05) • Null Hypothesis can be rejected • Performance is negatively correlated to service anxiety but positively correlated to time spent training

Exploring Relationships between Variables b. Mean Comparison

Independent Sample t-test ○ Compares the mean values of two different groups (μ 1 = μ 2) ○ If the mean values of two different groups are different (i. e. , μ 1 – μ 2 = 0), t-value will be significant (p <. 05) Dependent Variable ○ Measured by at least interval scale Independent Variable ○ Measured by categorical variable (e. g. , male/female, parttime/full-time, etc. )

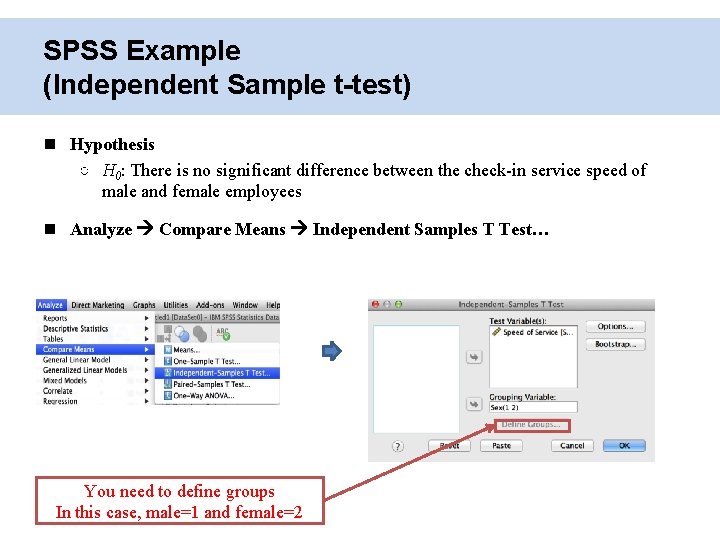
SPSS Example (Independent Sample t-test) Hypothesis ○ H 0: There is no significant difference between the check-in service speed of male and female employees Analyze Compare Means Independent Samples T Test… You need to define groups In this case, male=1 and female=2

SPSS Example (Independent Sample t-test) Results ○ Equal variance assumption check • If F-value is not significant (p >. 05), read ‘Equal variances assumed’ row • If F-value is significant (p <. 05), read “Equal variance not assumed’ row ○ t-value = – 2. 981 (p <. 05) • Null Hypothesis can be rejected • Speed of check-in service differs according to the gender of employees

Paired Sample t-test ○ Compares mean values of one group but measured at different times Independent Sample t-test vs. Paired Sample t-test ○ Independent sample t-test • Group: 2 different groups • Mean value: one for each group ○ Paired sample t-test • Group: 1 group • Mean value: two mean values measured at different times

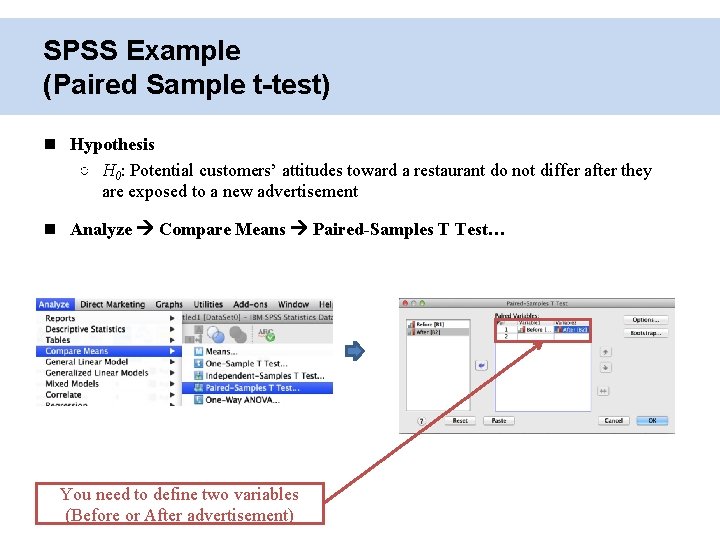
SPSS Example (Paired Sample t-test) Hypothesis ○ H 0: Potential customers’ attitudes toward a restaurant do not differ after they are exposed to a new advertisement Analyze Compare Means Paired-Samples T Test… You need to define two variables (Before or After advertisement)

SPSS Example (Paired Sample t-test) Results ○ t-value = – 12. 084 (p <. 05) • Null Hypothesis can be rejected • Potential customers’ attitudes toward a restaurant differs after they are exposed to a new advertisement

One-Way ANOVA ○ Mean comparison of more than two groups (or factor) Independent Sample t-test vs. One-Way ANOVA ○ Independent sample t-test • Mean comparison between two groups ○ One-way ANOVA • Mean comparison among more than two groups

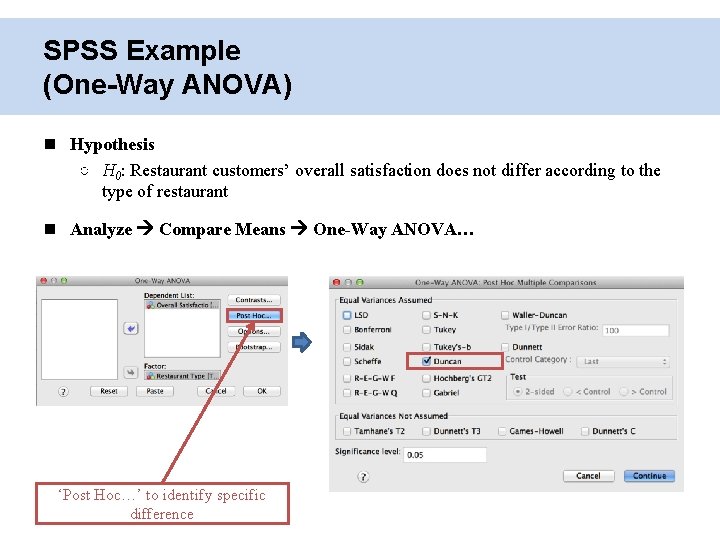
SPSS Example (One-Way ANOVA) Hypothesis ○ H 0: Restaurant customers’ overall satisfaction does not differ according to the type of restaurant Analyze Compare Means One-Way ANOVA… ‘Post Hoc…’ to identify specific difference

SPSS Example (One-Way ANOVA) Results #1 (ANOVA) ○ F-value = 16. 499 (p <. 05) • Null Hypothesis can be rejected • Restaurant customers’ overall satisfaction differs according to the type of restaurant Results #2 (Post-Hoc test) ○ Fast Food < Limited Service < Upscale Restaurant

Two-Way ANOVA ○ Compares the mean differences between groups that can be split on two independent variables (factors) ○ Commonly used to identify interaction effects Interaction Effect • Male Low vs. Female High • Female High vs. Male Low Gender Male Female Mean Education Level High Low μ Male High μ Male Low μ Female High μ Female Low μ High μ Low Mean μ Male μ Female μ Total Main Effect • High vs. Low • Male vs. Female

Exploring Relationships between Variables c. Causal Relationship

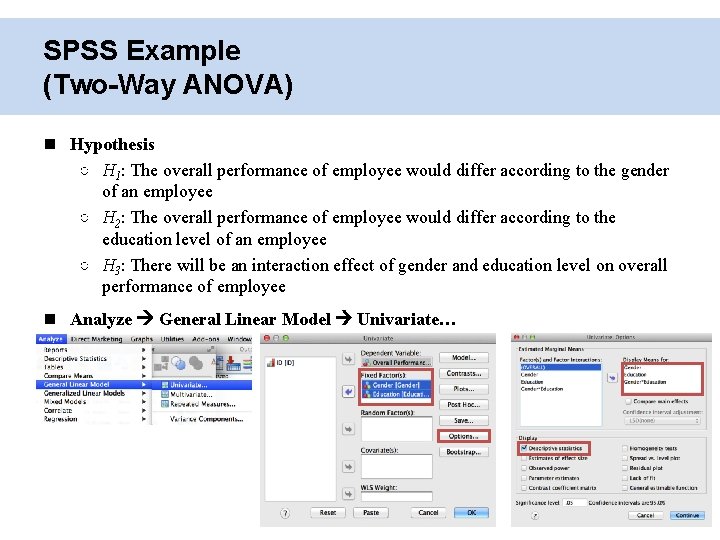
SPSS Example (Two-Way ANOVA) Hypothesis ○ H 1: The overall performance of employee would differ according to the gender of an employee ○ H 2: The overall performance of employee would differ according to the education level of an employee ○ H 3: There will be an interaction effect of gender and education level on overall performance of employee Analyze General Linear Model Univariate…

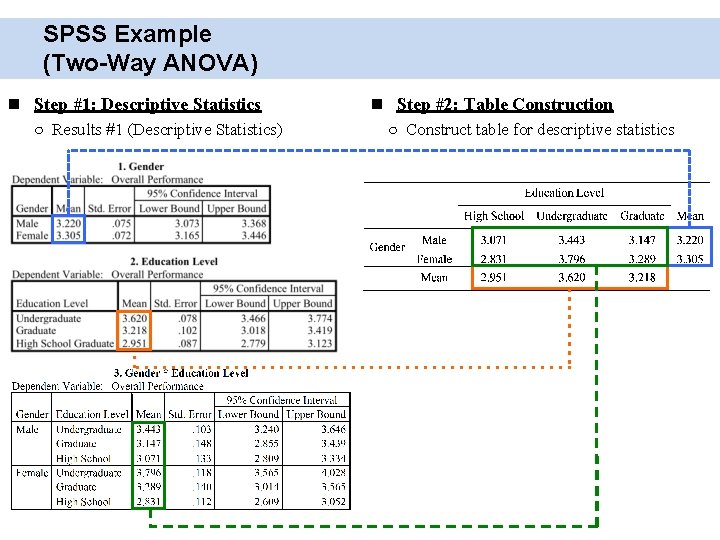
SPSS Example (Two-Way ANOVA) Step #1: Descriptive Statistics ○ Results #1 (Descriptive Statistics) Step #2: Table Construction ○ Construct table for descriptive statistics

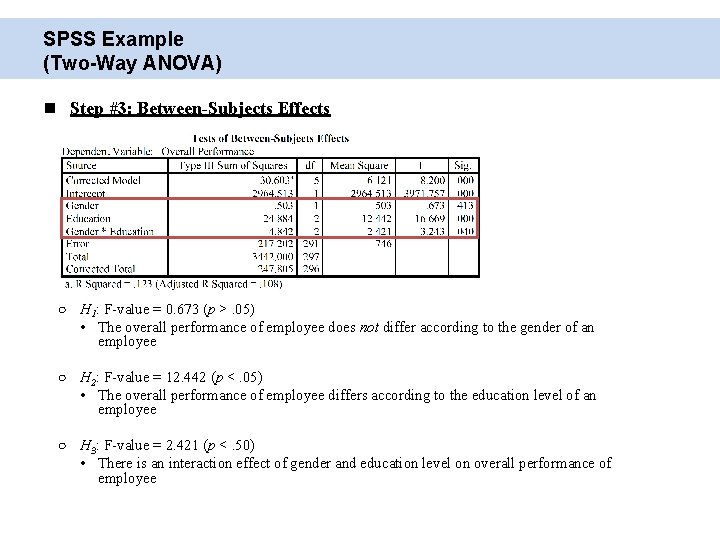
SPSS Example (Two-Way ANOVA) Step #3: Between-Subjects Effects ○ H 1: F-value = 0. 673 (p >. 05) • The overall performance of employee does not differ according to the gender of an employee ○ H 2: F-value = 12. 442 (p <. 05) • The overall performance of employee differs according to the education level of an employee ○ H 3: F-value = 2. 421 (p <. 50) • There is an interaction effect of gender and education level on overall performance of employee

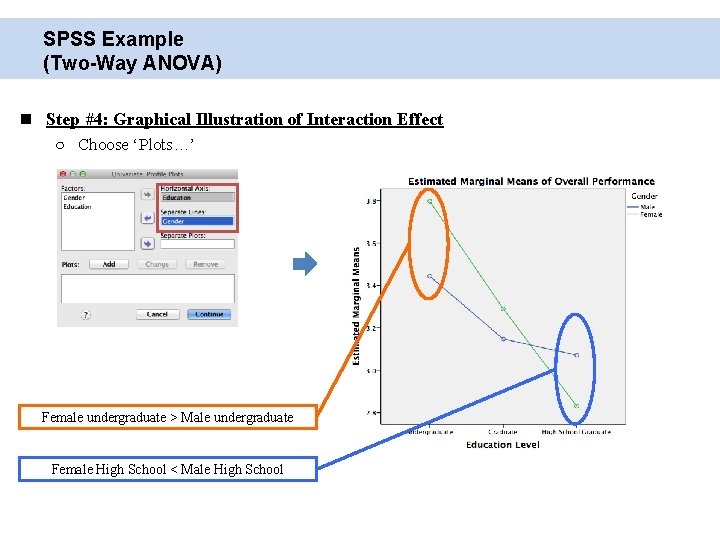
SPSS Example (Two-Way ANOVA) Step #4: Graphical Illustration of Interaction Effect ○ Choose ‘Plots…’ Female undergraduate > Male undergraduate Female High School < Male High School

Multiple Regression ○ Examine the simultaneous effects of several independent variables on a dependent variable Correlation vs. Regression ○ Correlation • No causal relationship ○ Regression • Causal relationship • A B (A causes B)

Multiple Regression Y = β 0 + β 1 X 1 + β 2 X 2 + β 3 X 3 + ε ○ Y: Dependent variable ○ X 1, X 2, and X 3: Independent variables ○ β 0: Intercept ○ β 1, β 2, and β 3: Regression coefficients ○ ε: Error term Regression is an approach for modeling the relationship between a dependent variable and one or more independent variables ○ The case of one independent variable is called simple linear regression ○ The case of more than one independent variables is called multiple linear regression Correlation vs. Regression ○ Regression can explain causal relationship but correlation cannot

Multiple Regression (Concepts to know) R 2 ○ The proportion of the original variance in dependent variable that is explained by the regression equation Multicollinearity ○ A problem referring to correlated independent variables • Causes unexpected signs • Small t-value ○ Can be detected by VIF and Tolerance

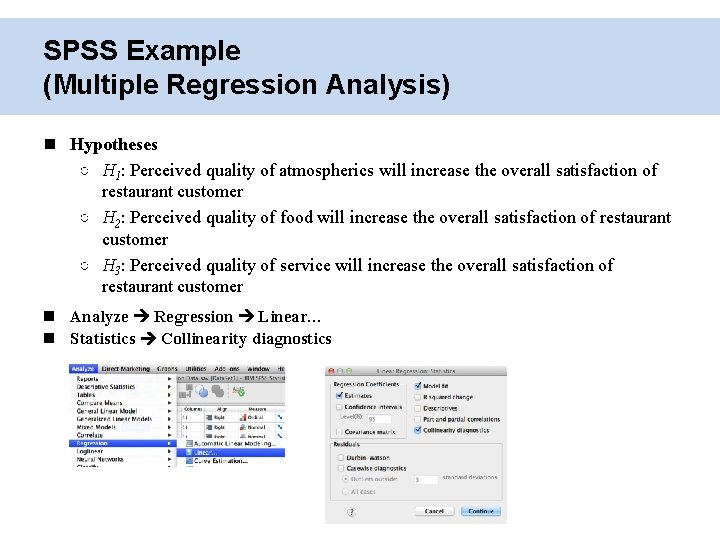
SPSS Example (Multiple Regression Analysis) Hypotheses ○ H 1: Perceived quality of atmospherics will increase the overall satisfaction of restaurant customer ○ H 2: Perceived quality of food will increase the overall satisfaction of restaurant customer ○ H 3: Perceived quality of service will increase the overall satisfaction of restaurant customer Analyze Regression Linear… Statistics Collinearity diagnostics

SPSS Example (Multiple Regression Analysis) Results #1 (Model Summary) ○ R 2 =. 311 • 31. 1% of total variance in Y has been explained by regression equation Results #2 (Post-Hoc test) ○ F-value = 43. 535 (p <. 05) • At least one coefficient is not equal to zero

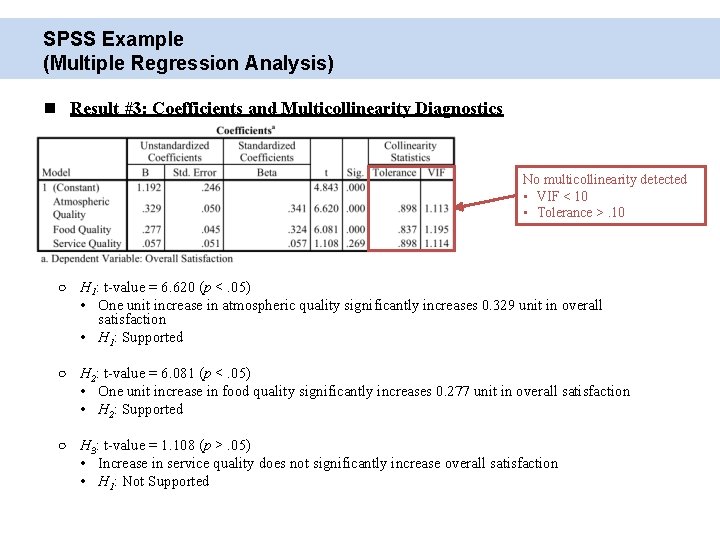
SPSS Example (Multiple Regression Analysis) Result #3: Coefficients and Multicollinearity Diagnostics No multicollinearity detected • VIF < 10 • Tolerance >. 10 ○ H 1: t-value = 6. 620 (p <. 05) • One unit increase in atmospheric quality significantly increases 0. 329 unit in overall satisfaction • H 1: Supported ○ H 2: t-value = 6. 081 (p <. 05) • One unit increase in food quality significantly increases 0. 277 unit in overall satisfaction • H 2: Supported ○ H 3: t-value = 1. 108 (p >. 05) • Increase in service quality does not significantly increase overall satisfaction • H 1: Not Supported

Exploring Relationships between Variables d. Advanced Methodologies

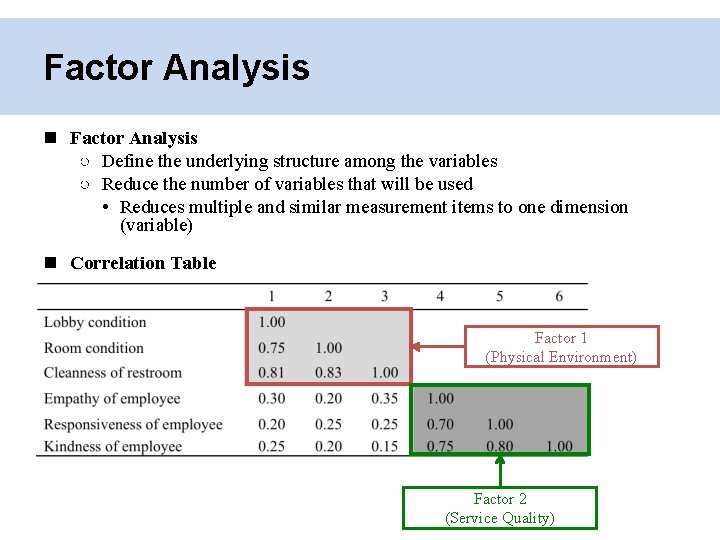
Factor Analysis ○ Define the underlying structure among the variables ○ Reduce the number of variables that will be used • Reduces multiple and similar measurement items to one dimension (variable) Correlation Table Factor 1 (Physical Environment) Factor 2 (Service Quality)

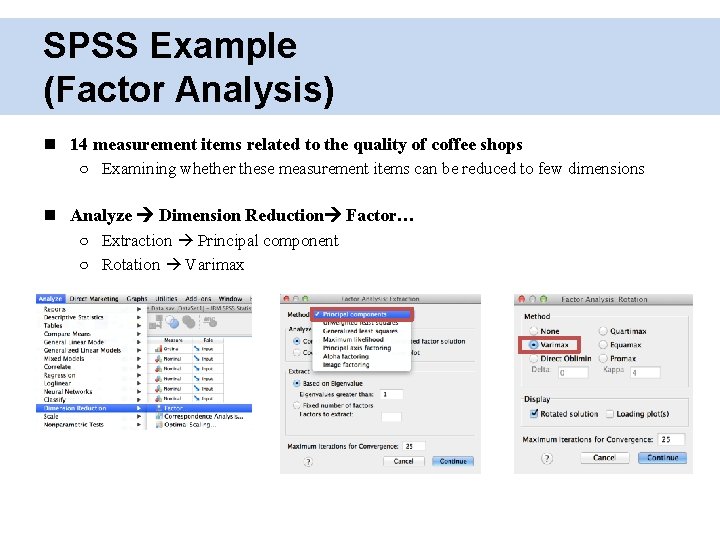
SPSS Example (Factor Analysis) 14 measurement items related to the quality of coffee shops ○ Examining whether these measurement items can be reduced to few dimensions Analyze Dimension Reduction Factor… ○ Extraction Principal component ○ Rotation Varimax

SPSS Example (Factor Analysis) Result #1: Communalities ○ The variance accounted for by the factors Result #2: Total Variance Explained ○ 4 Factors were identified and 67. 03% of total variance was explained

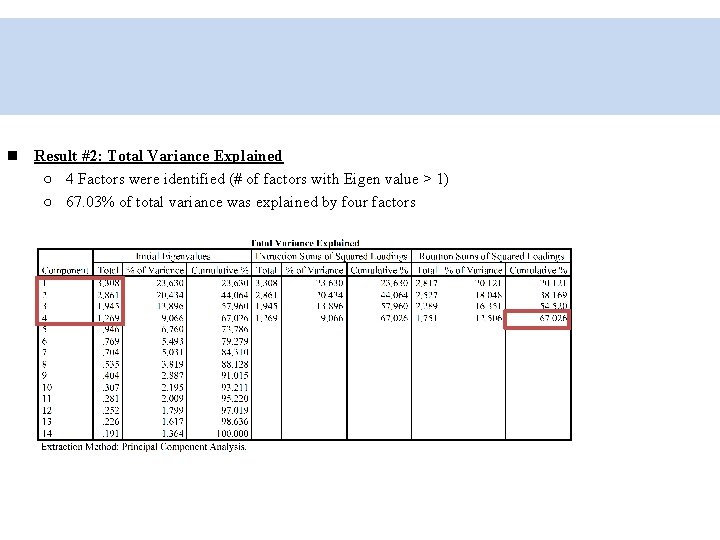
Result #2: Total Variance Explained ○ 4 Factors were identified (# of factors with Eigen value > 1) ○ 67. 03% of total variance was explained by four factors

SPSS Example (Factor Analysis) Result #3: Factor Loadings ○ Loadings lower than 0. 4 was not displayed Name each factor based on the measurement items included ○ ○ Factor 1: Value Factor 2: Advertisement Factor 3: Accessibility Factor 4: Coffee Quality

Utilization of Factors Utilization of Extracted Factors ○ Extracted factors in the previous example can be used for multiple regression analysis Things to consider 1. Utilization of factor scores • Standardized score – Mean = 0, Standard Deviation = 1 2. Utilization of mean value • Calculate mean value for measurement items included in each factor – Mean ≠ 0, Standard Deviation ≠ 1

SPSS Example (Factor Score + Multiple Regression Analysis) Hypotheses ○ H 1: Perceived value will increase the overall satisfaction of coffee shop customer ○ H 2: Perceived quality of advertisement will increase the overall satisfaction of coffee shop customer ○ H 3: Perceived quality of accessibility will increase the overall satisfaction of coffee shop customer ○ H 4: Perceived quality of coffee will increase the overall satisfaction of coffee shop customer Analyze Dimension Reduction Factor… Score ○ Save as variables Analyze Regression Linear… (Move factor scores as independent variables)

SPSS Example (Factor Score + Multiple Regression Analysis) Results ○ R 2 = 0. 314 ○ F-value = 32. 337 ○ VIF, Tolerance = 1 (No multicollinearity) • Varimax rotation minimizes correlation between dimensions Hypotheses Testing ○ H 1: Perceived value significantly increase the overall satisfaction (Supported) ○ H 2: Perceived quality of advertisement does not have significant influence on the overall satisfaction (Not supported) ○ H 3: Perceived quality of accessibility does not have significant influence on the overall satisfaction (Not supported) ○ H 4: Perceived quality of coffee significantly increase the overall satisfaction (Supported)

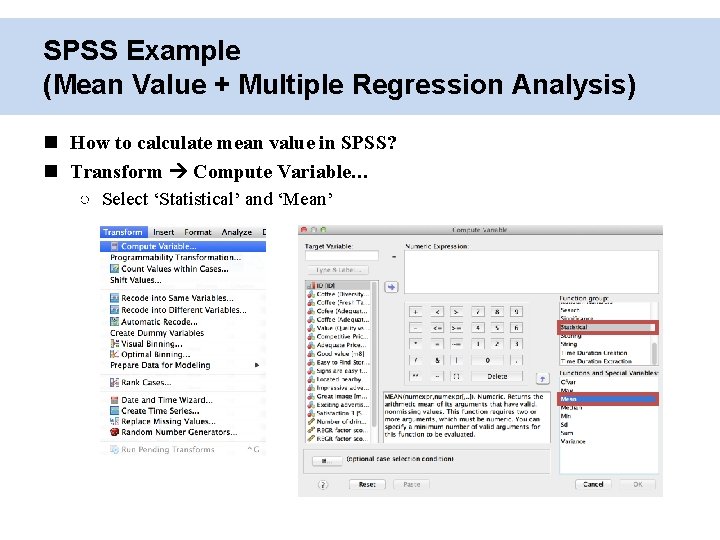
SPSS Example (Mean Value + Multiple Regression Analysis) How to calculate mean value in SPSS? Transform Compute Variable… ○ Select ‘Statistical’ and ‘Mean’

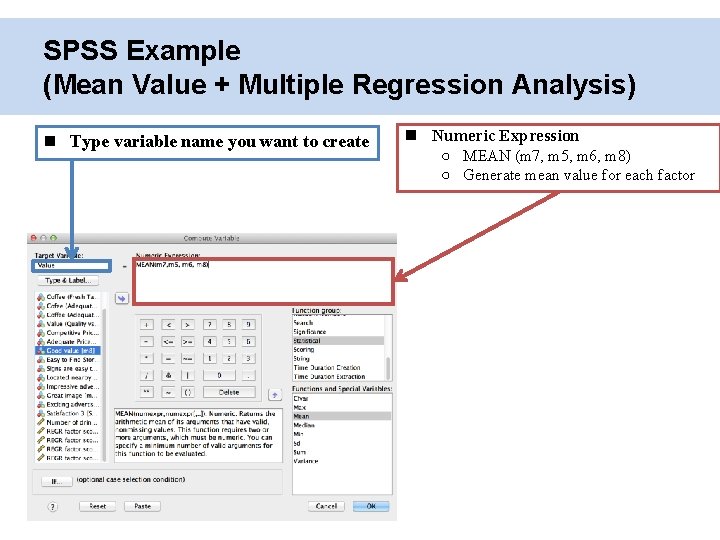
SPSS Example (Mean Value + Multiple Regression Analysis) Type variable name you want to create Numeric Expression ○ MEAN (m 7, m 5, m 6, m 8) ○ Generate mean value for each factor

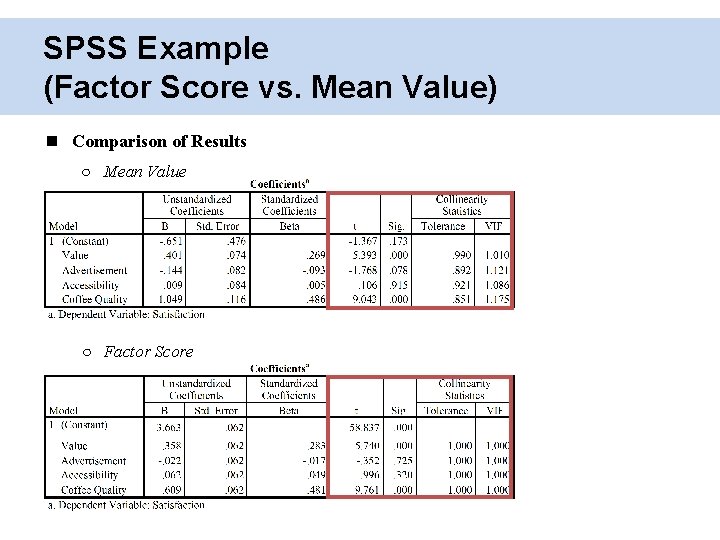
SPSS Example (Factor Score vs. Mean Value) Comparison of Results ○ Mean Value ○ Factor Score

SPSS Example (Factor Score vs. Mean Value) Similarity ○ Standardized β ○ Sign of coefficients ○ Significance level Differences ○ Unstandardized coefficients ○ t-value ○ Collinearity diagnostics • Varimax Rotation: No collinearity at all • Mean Value: Collinearity may exist Utilization of factor score or mean score depends on researcher’s decision