Chapter 10 Limits and the Derivative Section 7

  • Slides: 28
Download presentation
Chapter 10 Limits and the Derivative Section 7 Marginal Analysis in Business and Economics

Chapter 10 Limits and the Derivative Section 7 Marginal Analysis in Business and Economics

Objectives for Section 10. 7 Marginal Analysis The student will be able to compute:

Objectives for Section 10. 7 Marginal Analysis The student will be able to compute: ■ Marginal cost, revenue and profit ■ Marginal average cost, revenue and profit ■ The student will be able to solve applications Barnett/Ziegler/Byleen College Mathematics 12 e 2

Marginal Cost Remember that marginal refers to an instantaneous rate of change, that is,

Marginal Cost Remember that marginal refers to an instantaneous rate of change, that is, a derivative. Definition: If x is the number of units of a product produced in some time interval, then Total cost = C(x) Marginal cost = C (x) Barnett/Ziegler/Byleen College Mathematics 12 e 3

Marginal Revenue and Marginal Profit Definition: If x is the number of units of

Marginal Revenue and Marginal Profit Definition: If x is the number of units of a product sold in some time interval, then Total revenue = R(x) Marginal revenue = R (x) If x is the number of units of a product produced and sold in some time interval, then Total profit = P(x) = R(x) – C(x) Marginal profit = P (x) = R (x) – C (x) Barnett/Ziegler/Byleen College Mathematics 12 e 4

Marginal Cost and Exact Cost Assume C(x) is the total cost of producing x

Marginal Cost and Exact Cost Assume C(x) is the total cost of producing x items. Then the exact cost of producing the (x + 1)st item is C(x + 1) – C(x). The marginal cost is an approximation of the exact cost. C (x) ≈ C(x + 1) – C(x). Similar statements are true for revenue and profit. Barnett/Ziegler/Byleen College Mathematics 12 e 5

Example 1 The total cost of producing x electric guitars is C(x) = 1,

Example 1 The total cost of producing x electric guitars is C(x) = 1, 000 + 100 x – 0. 25 x 2. 1. Find the exact cost of producing the 51 st guitar. 2. Use the marginal cost to approximate the cost of producing the 51 st guitar. Barnett/Ziegler/Byleen College Mathematics 12 e 6

Example 1 (continued) The total cost of producing x electric guitars is C(x) =

Example 1 (continued) The total cost of producing x electric guitars is C(x) = 1, 000 + 100 x – 0. 25 x 2. 1. Find the exact cost of producing the 51 st guitar. The exact cost is C(x + 1) – C(x). C(51) – C(50) = 5, 449. 75 – 5375 = $74. 75. 2. Use the marginal cost to approximate the cost of producing the 51 st guitar. The marginal cost is C (x) = 100 – 0. 5 x C (50) = $75. Barnett/Ziegler/Byleen College Mathematics 12 e 7

Marginal Average Cost Definition: If x is the number of units of a product

Marginal Average Cost Definition: If x is the number of units of a product produced in some time interval, then Average cost per unit = Marginal average cost = Barnett/Ziegler/Byleen College Mathematics 12 e 8

Marginal Average Revenue Marginal Average Profit If x is the number of units of

Marginal Average Revenue Marginal Average Profit If x is the number of units of a product sold in some time interval, then Average revenue per unit = Marginal average revenue = If x is the number of units of a product produced and sold in some time interval, then Average profit per unit = Marginal average profit = Barnett/Ziegler/Byleen College Mathematics 12 e 9

Warning! To calculate the marginal averages you must calculate the average first (divide by

Warning! To calculate the marginal averages you must calculate the average first (divide by x), and then the derivative. If you change this order you will get no useful economic interpretations. Barnett/Ziegler/Byleen College Mathematics 12 e STO P 10

Example 2 The total cost of printing x dictionaries is C(x) = 20, 000

Example 2 The total cost of printing x dictionaries is C(x) = 20, 000 + 10 x 1. Find the average cost per unit if 1, 000 dictionaries are produced. Barnett/Ziegler/Byleen College Mathematics 12 e 11

Example 2 (continued) The total cost of printing x dictionaries is C(x) = 20,

Example 2 (continued) The total cost of printing x dictionaries is C(x) = 20, 000 + 10 x 1. Find the average cost per unit if 1, 000 dictionaries are produced. = $30 Barnett/Ziegler/Byleen College Mathematics 12 e 12

Example 2 (continued) 2. Find the marginal average cost at a production level of

Example 2 (continued) 2. Find the marginal average cost at a production level of 1, 000 dictionaries, and interpret the results. Barnett/Ziegler/Byleen College Mathematics 12 e 13

Example 2 (continued) 2. Find the marginal average cost at a production level of

Example 2 (continued) 2. Find the marginal average cost at a production level of 1, 000 dictionaries, and interpret the results. Marginal average cost = This means that if you raise production from 1, 000 to 1, 001 dictionaries, the price per book will fall approximately 2 cents. Barnett/Ziegler/Byleen College Mathematics 12 e 14

Example 2 (continued) 3. Use the results from above to estimate the average cost

Example 2 (continued) 3. Use the results from above to estimate the average cost per dictionary if 1, 001 dictionaries are produced. Barnett/Ziegler/Byleen College Mathematics 12 e 15

Example 2 (continued) 3. Use the results from above to estimate the average cost

Example 2 (continued) 3. Use the results from above to estimate the average cost per dictionary if 1, 001 dictionaries are produced. Average cost for 1000 dictionaries = $30. 00 Marginal average cost = - 0. 02 The average cost per dictionary for 1001 dictionaries would be the average for 1000, plus the marginal average cost, or $30. 00 + $(- 0. 02) = $29. 98 Barnett/Ziegler/Byleen College Mathematics 12 e 16

Example 3 The price-demand equation and the cost function for the production of television

Example 3 The price-demand equation and the cost function for the production of television sets are given by where x is the number of sets that can be sold at a price of $p per set, and C(x) is the total cost of producing x sets. 1. Find the marginal cost. Barnett/Ziegler/Byleen College Mathematics 12 e 17

Example 3 (continued) The price-demand equation and the cost function for the production of

Example 3 (continued) The price-demand equation and the cost function for the production of television sets are given by where x is the number of sets that can be sold at a price of $p per set, and C(x) is the total cost of producing x sets. 1. Find the marginal cost. Solution: The marginal cost is C (x) = $30. Barnett/Ziegler/Byleen College Mathematics 12 e 18

Example 3 (continued) 2. Find the revenue function in terms of x. Barnett/Ziegler/Byleen College

Example 3 (continued) 2. Find the revenue function in terms of x. Barnett/Ziegler/Byleen College Mathematics 12 e 19

Example 3 (continued) 2. Find the revenue function in terms of x. The revenue

Example 3 (continued) 2. Find the revenue function in terms of x. The revenue function is 3. Find the marginal revenue. Barnett/Ziegler/Byleen College Mathematics 12 e 20

Example 3 (continued) 2. Find the revenue function in terms of x. The revenue

Example 3 (continued) 2. Find the revenue function in terms of x. The revenue function is 3. Find the marginal revenue. The marginal revenue is 4. Find R (1500) and interpret the results. Barnett/Ziegler/Byleen College Mathematics 12 e 21

Example 3 (continued) 2. Find the revenue function in terms of x. The revenue

Example 3 (continued) 2. Find the revenue function in terms of x. The revenue function is 3. Find the marginal revenue. The marginal revenue is 4. Find R (1500) and interpret the results. At a production rate of 1, 500, each additional set increases revenue by approximately $200. Barnett/Ziegler/Byleen College Mathematics 12 e 22

Example 3 (continued) 5. Graph the cost function and the revenue function on the

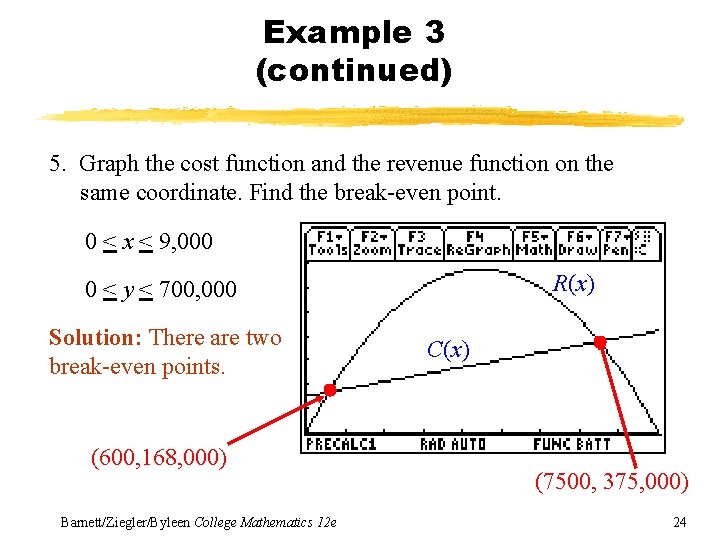
Example 3 (continued) 5. Graph the cost function and the revenue function on the same coordinate. Find the break-even point. 0 < x < 9, 000 0 < y < 700, 000 Barnett/Ziegler/Byleen College Mathematics 12 e 23

Example 3 (continued) 5. Graph the cost function and the revenue function on the

Example 3 (continued) 5. Graph the cost function and the revenue function on the same coordinate. Find the break-even point. 0 < x < 9, 000 R(x) 0 < y < 700, 000 Solution: There are two break-even points. (600, 168, 000) Barnett/Ziegler/Byleen College Mathematics 12 e C(x) (7500, 375, 000) 24

Example 3 (continued) 6. Find the profit function in terms of x. Barnett/Ziegler/Byleen College

Example 3 (continued) 6. Find the profit function in terms of x. Barnett/Ziegler/Byleen College Mathematics 12 e 25

Example 3 (continued) 6. Find the profit function in terms of x. The profit

Example 3 (continued) 6. Find the profit function in terms of x. The profit is revenue minus cost, so 7. Find the marginal profit. Barnett/Ziegler/Byleen College Mathematics 12 e 26

Example 3 (continued) 6. Find the profit function in terms of x. The profit

Example 3 (continued) 6. Find the profit function in terms of x. The profit is revenue minus cost, so 7. Find the marginal profit. 8. Find P (1500) and interpret the results. Barnett/Ziegler/Byleen College Mathematics 12 e 27

Example 3 (continued) 6. Find the profit function in terms of x. The profit

Example 3 (continued) 6. Find the profit function in terms of x. The profit is revenue minus cost, so 7. Find the marginal profit. 8. Find P’(1500) and interpret the results. At a production level of 1500 sets, profit is increasing at a rate of about $170 per set. Barnett/Ziegler/Byleen College Mathematics 12 e 28

LIMITS LIMITS STANDARD LIMITS LIMITS STANDARD LIMITS LIMITSLIMITS LIMITS STANDARD LIMITS LIMITS STANDARD LIMITS LIMITS
Derivative By Artineer Derivative Derivative Linear Regression ByDerivative By Artineer Derivative Derivative Linear Regression By
Chapter 3 Limits and the Derivative Section 5Chapter 3 Limits and the Derivative Section 5
Chapter 3 Limits and the Derivative Section 2Chapter 3 Limits and the Derivative Section 2
Chapter 10 Limits and the Derivative Section RChapter 10 Limits and the Derivative Section R
Chapter 10 Limits and the Derivative Section 5Chapter 10 Limits and the Derivative Section 5
Chapter 2 Limits and the Derivative Section 3Chapter 2 Limits and the Derivative Section 3
Chapter 2 Limits and the Derivative Section 7Chapter 2 Limits and the Derivative Section 7
Chapter 10 Limits and the Derivative Section 2Chapter 10 Limits and the Derivative Section 2
Chapter 2 Limits and the Derivative Section 2Chapter 2 Limits and the Derivative Section 2
Chapter 2 Limits and the Derivative Section 1Chapter 2 Limits and the Derivative Section 1
Chapter 3 Limits and the Derivative Section 3Chapter 3 Limits and the Derivative Section 3
Limits I Why limits II What are limitsLimits I Why limits II What are limits
LIMITS Why limits Methods for upper limits DesirableLIMITS Why limits Methods for upper limits Desirable
Understanding Limits Limits Limits are the foundation ofUnderstanding Limits Limits Limits are the foundation of
Limits Peter Gibby Limits Limits are a wayLimits Peter Gibby Limits Limits are a way
LIMITS LIMITS INTRODUCTION LIMITS v Consider the sequencesLIMITS LIMITS INTRODUCTION LIMITS v Consider the sequences
Guidance Techniques SETTING LIMITS Setting Limits What limitsGuidance Techniques SETTING LIMITS Setting Limits What limits
2 LIMITS LIMITS 2 3 Calculating Limits Using2 LIMITS LIMITS 2 3 Calculating Limits Using
Graphs Extra Limits Extra Limits Extra Limits ExtraGraphs Extra Limits Extra Limits Extra Limits Extra
Loan Limits FHA Loan Limits FHA loan limitsLoan Limits FHA Loan Limits FHA loan limits
Derivatives and its variants Derivative Definition A derivativeDerivatives and its variants Derivative Definition A derivative
Differentiation and the Derivative A derivative is obtainedDifferentiation and the Derivative A derivative is obtained
Hedging Risk Derivative Securities Derivative Markets l lHedging Risk Derivative Securities Derivative Markets l l