CHAPTER 10 Inferential Statistics 10 1 Confidence Intervals

CHAPTER 10 Inferential Statistics 10. 1 Confidence Intervals

Statistical Inference n n n Statistical Inference provides methods for drawing conclusions about a population from sample data. Consider what the population mean must be, based on. Consider what the population proportion must be, based on.

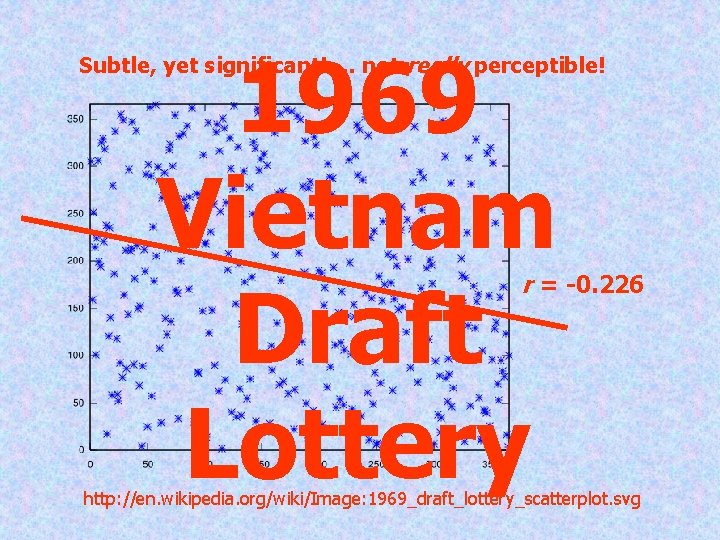
Draft Lotteries & Drug Studies n n With an r = -0. 226 – was there something “funny going on” – unfair – with the Vietnam Draft? Well … P < 0. 001 What if 40 patients were split into two groups to get a drug. 20 get the real thing; 20 get the Placebo. 12 feel better in the real group; 8 in the Placebo. So? Turns out P is about 0. 2 … not too rare.

1969 Vietnam Draft Lottery Subtle, yet significant! … not really perceptible! r = -0. 226 http: //en. wikipedia. org/wiki/Image: 1969_draft_lottery_scatterplot. svg

Consequences It was quickly noticed that draft ranks were not uniformly distributed over the year. In particular, birthdays in December had lower (earlier) draft ranks, on average, than birthdays in other months. This led to complaints that the lottery was not random as the legislation required. Analysis of the lottery method suggested that the procedure (mixing the capsules in the shoe box and dumping them into the jar) did not mix the capsules sufficiently, however the-less-thanrandom lottery was allowed to stand. The lottery system was later modified to produce a more random result.

SAT MATH in CALIFORNIA n N = 350, 000 … n = 500 … n n The margin of error for a 95% CI: n n “We are 95% confident that this interval contains the true population mean score for all California Seniors”

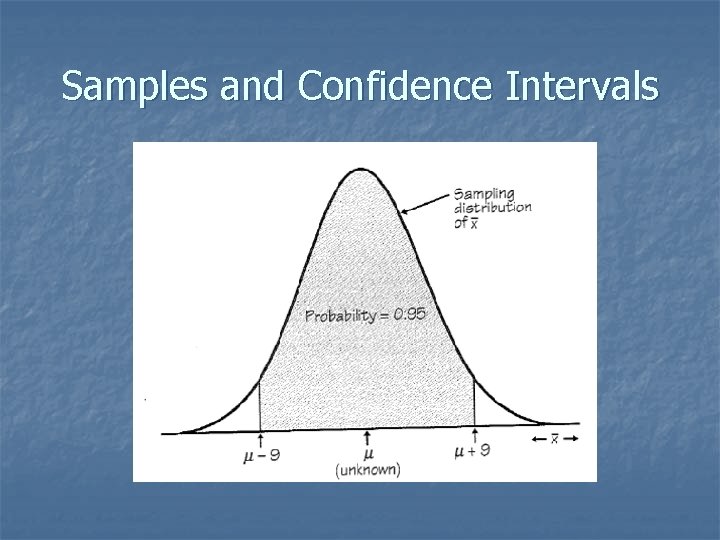
Samples and Confidence Intervals

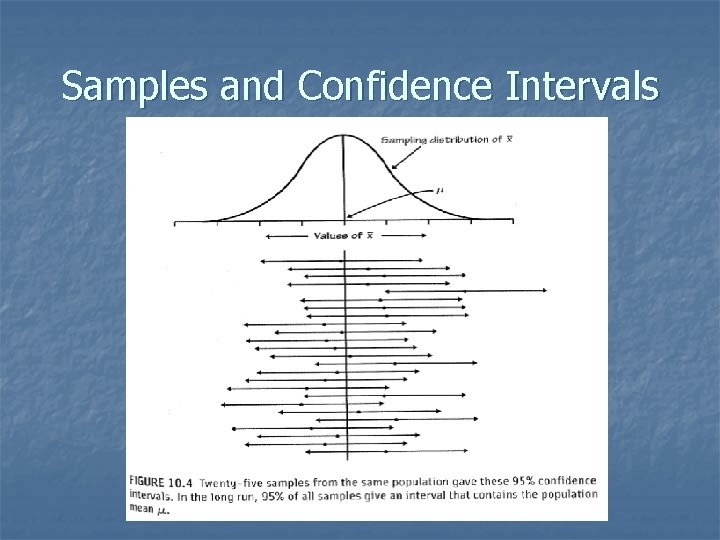
Samples and Confidence Intervals

Samples and Confidence Intervals

Conditions n It is appropriate to construct a Confidence Interval only when: n The data were chosen randomly from the population of interest n The sampling distribution is approximately normal n The individuals in the sample were independently chosen n The Population is at least ten times as big as the sample

From z to z* n n n The z value is something we have calculated with known values of x, mu, and sigma. NOW – we know what we want to set out area at … our Confidence Level dictates that. z* is just the perfect value of z to create a desired level of confidence.

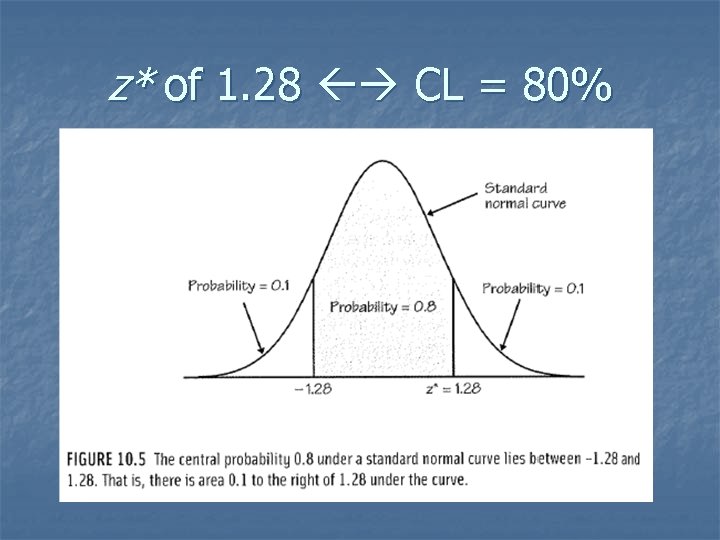
z* of 1. 28 CL = 80%

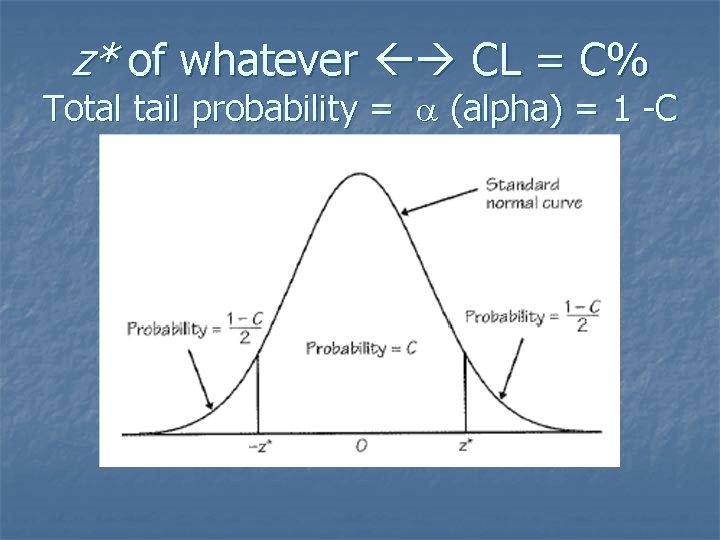
z* of whatever CL = C% Total tail probability = (alpha) = 1 -C

Typical z-values n 90% CL tail area =. 05 z* = 1. 645 n 95% CL tail area =. 025 z* = 1. 960 n 99% CL tail area =. 005 z* = 2. 576

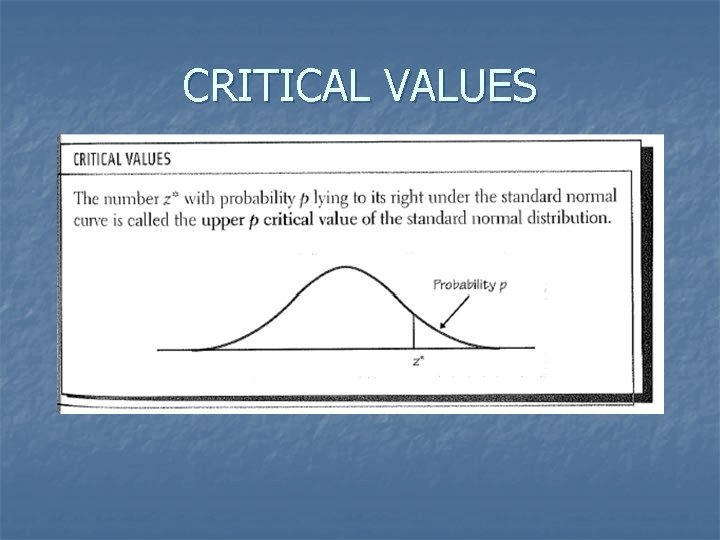
CRITICAL VALUES

CONFIDENCE INTERVAL FOR A POPULATION MEAN

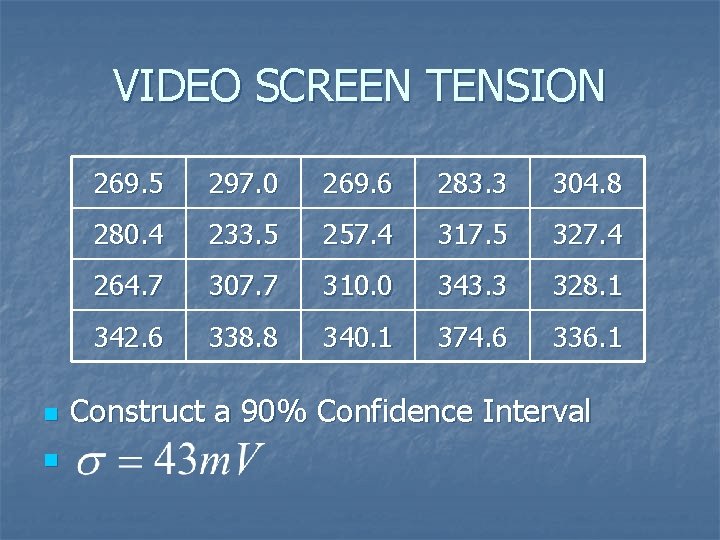
VIDEO SCREEN TENSION n n 269. 5 297. 0 269. 6 283. 3 304. 8 280. 4 233. 5 257. 4 317. 5 327. 4 264. 7 307. 7 310. 0 343. 3 328. 1 342. 6 338. 8 340. 1 374. 6 336. 1 Construct a 90% Confidence Interval

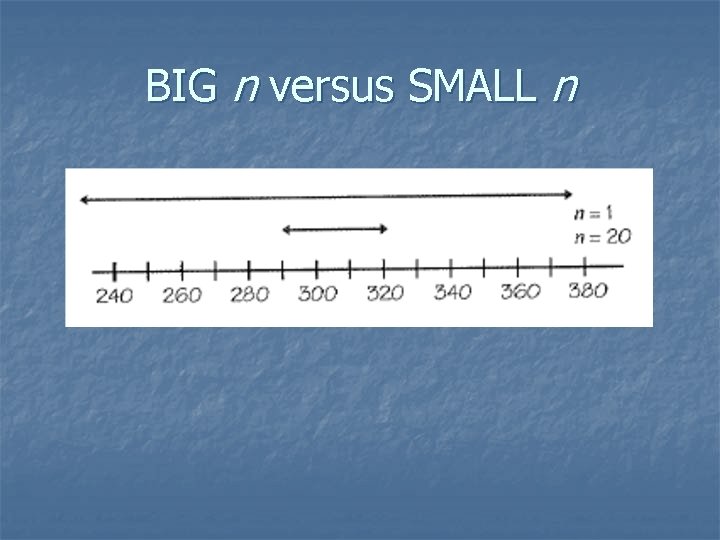
BIG n versus SMALL n

INFERENCE TOOLBOX n Step 1: Identify the population and n Step 2: Chose the appropriate Inference parameter to be inferred Procedure – Verify Conditions n Step 3: CI = estimate ± margin of error n Step 4: Interpret

10. 6: SURVEYING HOTEL MANAGERS

COMPARATIVE EFFECTS OF z, , and n Making z smaller … Bigger? n Making n smaller … Bigger? n By what factor do we need to increase the sample size by to reduce the margin of error by one-half? n

VIDEO SCREEN TENSION (revisited) n Make a 99% CI now instead

CHOOSING A SAMPLE SIZE n n The company that we are still working with wants to report the screen tension within ± 5 m. V with 95% confidence. What sample size will achieve this?

CAUTIONS Careful with RANDOM SRSs n Only SRSs – no stratified n Watch bias in data collection – cannot be mathematically “corrected” n Watch out for outliers – eliminate? n Watch for skewing – or any non. Normality – as the true C-level will not be accurate n YOU MUST KNOW . n Confidence is not Probability n