Chapter 10 Correlation and Regression Section 103 Correlation




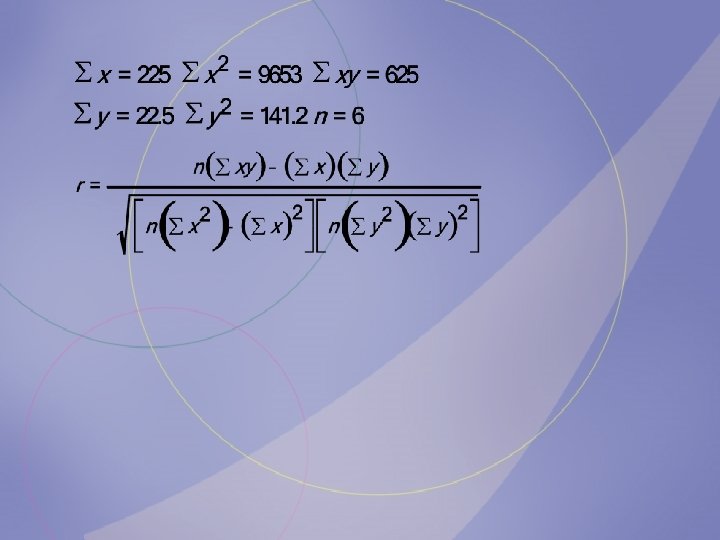
















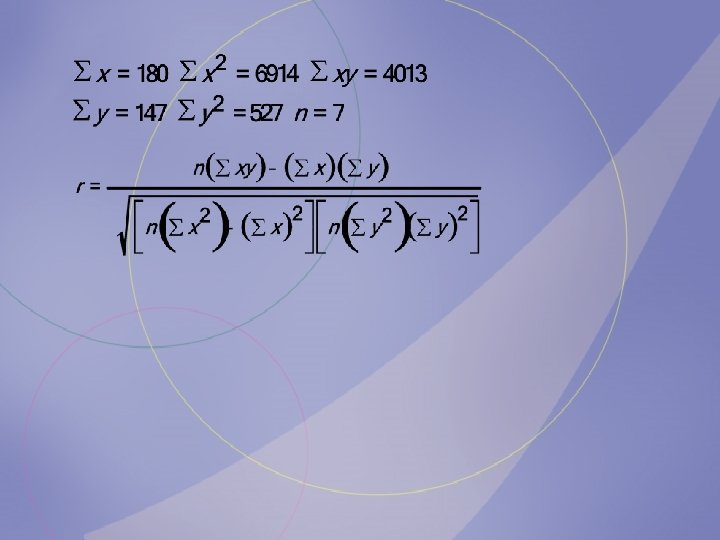







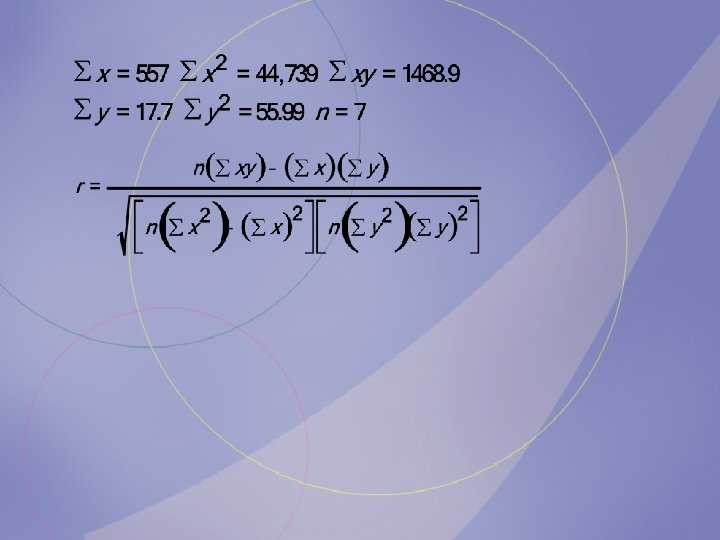



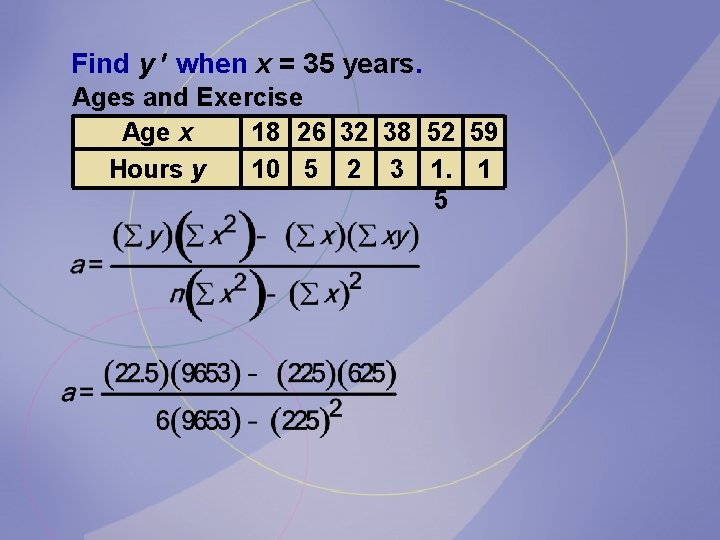
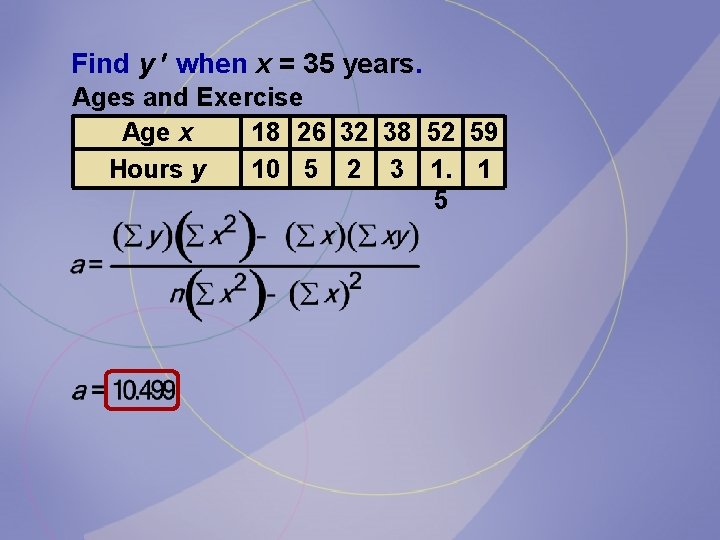
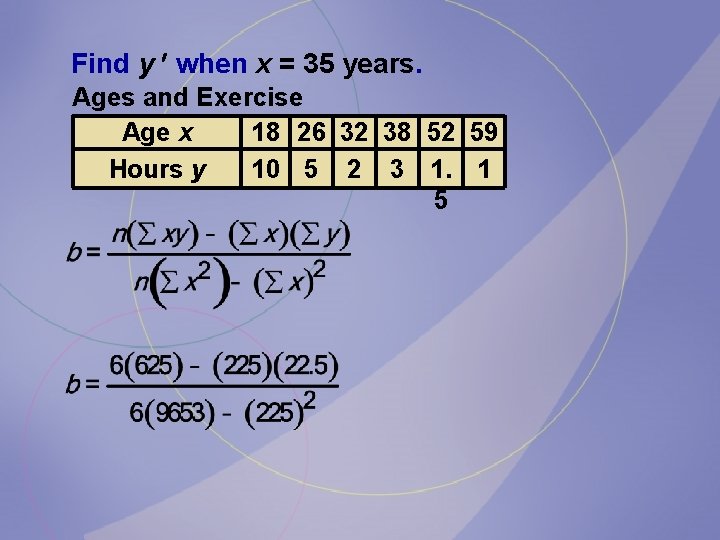
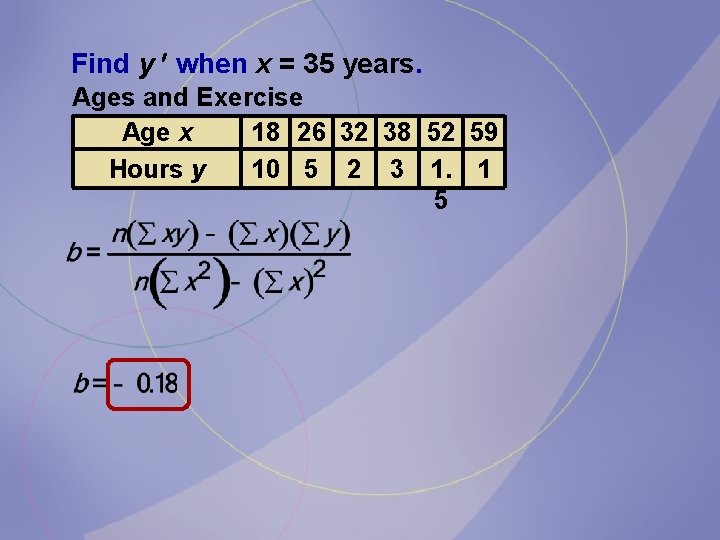

































- Slides: 81

Chapter 10 Correlation and Regression Section 103 Correlation

Chapter 10 Correlation and Regression Section 103 Exercise #13

For the following exercise, complete these steps. a. Draw the scatter plot for the variables. b. Compute the value of the correlation coefficient. c. State the hypotheses. d. Test the significance of the correlation coefficient at = 0. 05, using Table I. e. Give a brief explanation of the type of relationship.

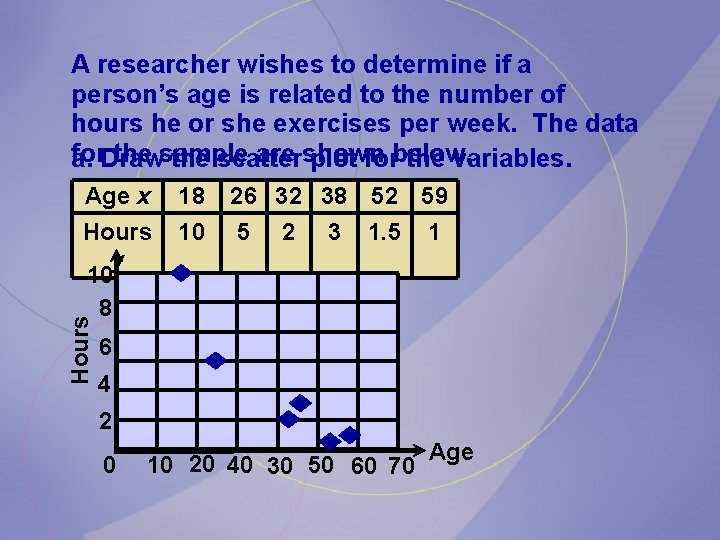
A researcher wishes to determine if a person’s age is related to the number of hours he or she exercises per week. The data for. Draw the sample are shown a. the scatter plot forbelow. the variables. 18 26 32 38 52 59 Hours y 10 8 10 5 Hours Age x 2 3 1. 5 1 6 4 2 0 10 20 40 30 50 60 70 Age

b. Compute the value of the correlation coefficient. Age x 18 26 32 38 52 59 Hours y 10 5 2 3 1. 5 1
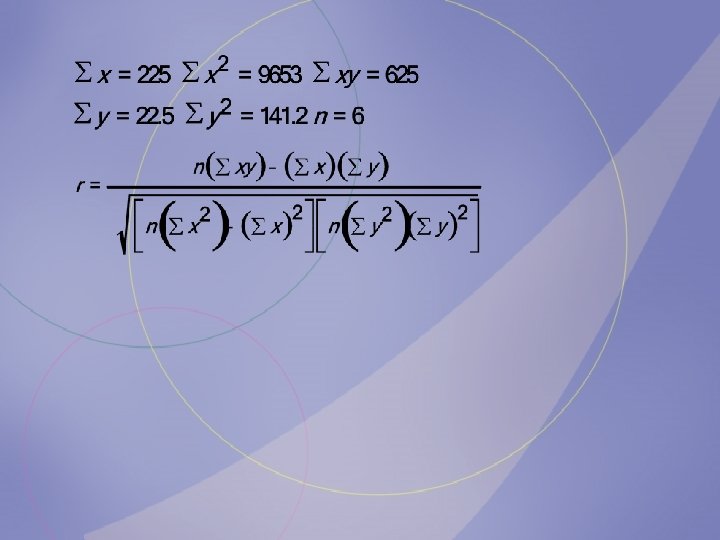


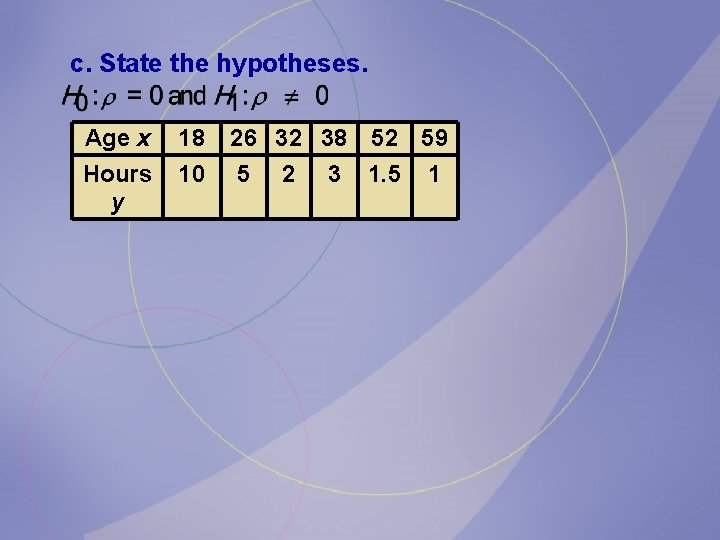
c. State the hypotheses. Age x 18 26 32 38 52 59 Hours y 10 5 2 3 1. 5 1

d. Test the significance of the correlation coefficient at = 0. 05, using Table I. Age x 18 26 32 38 52 59 Hours y 10 5 2 3 1. 5 1

e. Give a brief explanation of the type of relationship. Age x 18 26 32 38 52 59 Hours y 10 5 2 3 1. 5 There is a significant linear relationship between a person’s age and the number of hours he or she exercises per week. 1

Chapter 10 Correlation and Regression Section 103 Exercise #15

For the following exercise, complete these steps. a. Draw the scatter plot for the variables. b. Compute the value of the correlation coefficient. c. State the hypotheses. d. Test the significance of the correlation coefficient at = 0. 05, using Table I. e. Give a brief explanation of the type of relationship.

The director of an alumni association for a small college wants to determine whethere is any type of relationship between the amount of an alumnus’s contribution (in dollars) and the years the alumnus has been out of school. The datax are 1 shown Years 5 3 here. 1 7 6 0 Contributio 50 10 30 5 ny 0 0 7 5 8 0

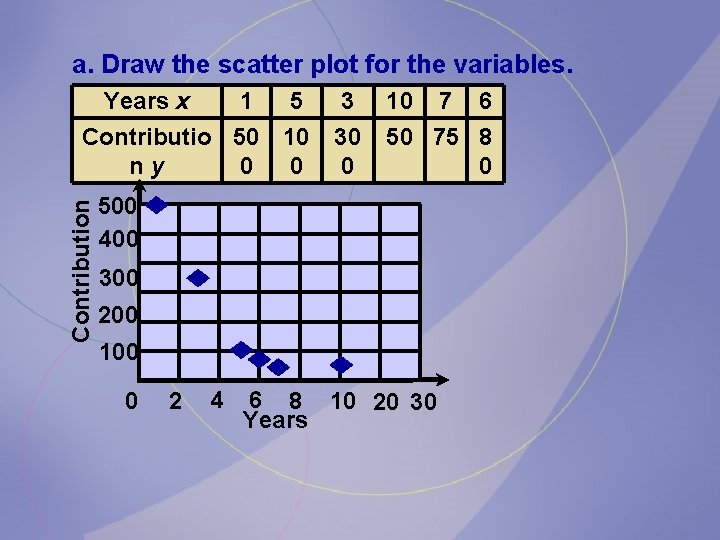
a. Draw the scatter plot for the variables. 5 3 10 Contributio 50 10 ny 0 0 30 0 50 75 8 0 Contribution Years x 1 500 400 300 200 100 0 2 4 6 8 10 20 30 Years 7 6

b. Compute the value of the correlation coefficient. Years x 1 5 3 10 7 6 Contributio 50 10 ny 0 0 30 0 50 75 8 0

b. Compute the value of the correlation coefficient.

b. Compute the value of the correlation coefficient.

c. State the hypotheses. Years x 1 5 3 10 7 6 Contributio 50 10 ny 0 0 30 0 50 75 8 0

d. Test the significance of the correlation coefficient at = 0. 05, using Table I. Years x 1 5 3 10 7 6 Contributio 50 10 ny 0 0 30 0 50 75 8 0

e. Give a brief explanation of the type of relationship. Years x 1 5 3 10 Contributio 50 10 ny 0 0 30 0 50 75 8 0 There is a significant linear relationship between a person’s age and his or her contribution. 7 6

Chapter 10 Correlation and Regression Section 103 Exercise #17

For the following exercise, complete these steps. a. Draw the scatter plot for the variables. b. Compute the value of the correlation coefficient. c. State the hypotheses. d. Test the significance of the correlation coefficient at = 0. 05, using Table I. e. Give a brief explanation of the type of relationship.

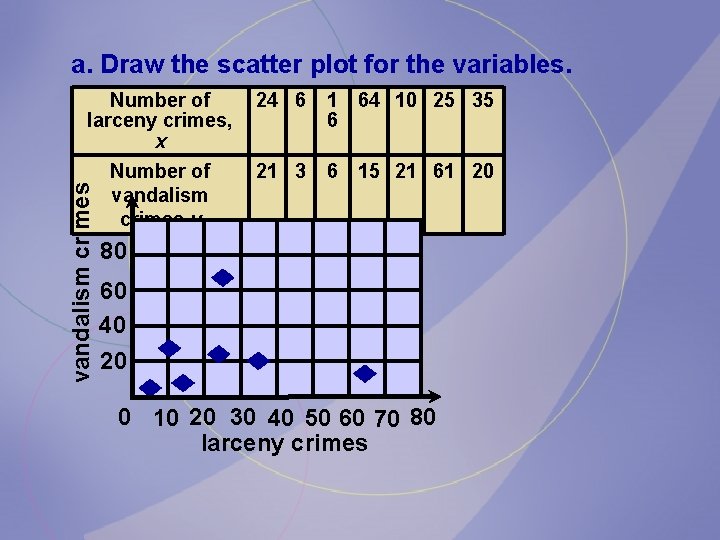
A criminology student wishes to see if there is a relationship between the number of larceny crimes and the number of vandalism crimes on college campuses in Southwestern Pennsylvania. The data are shown. Is there a relationship between the two types of crimes? Number of 2 6 1 2 3 larceny crimes, x Number of vandalism crimes y 4 6 4 0 5 5 2 3 6 1 1 5 2 1 6 1 2 0

a. Draw the scatter plot for the variables. 24 6 1 64 10 25 35 6 Number of vandalism crimes y 21 3 6 15 21 61 20 vandalism crimes Number of larceny crimes, x 80 60 40 20 0 10 20 30 40 50 60 70 80 larceny crimes

b. Compute the value of the correlation coefficient. Number of 24 6 1 64 10 25 35 larceny crimes, x Number of vandalism crimes y 6 21 3 6 15 21 61 20
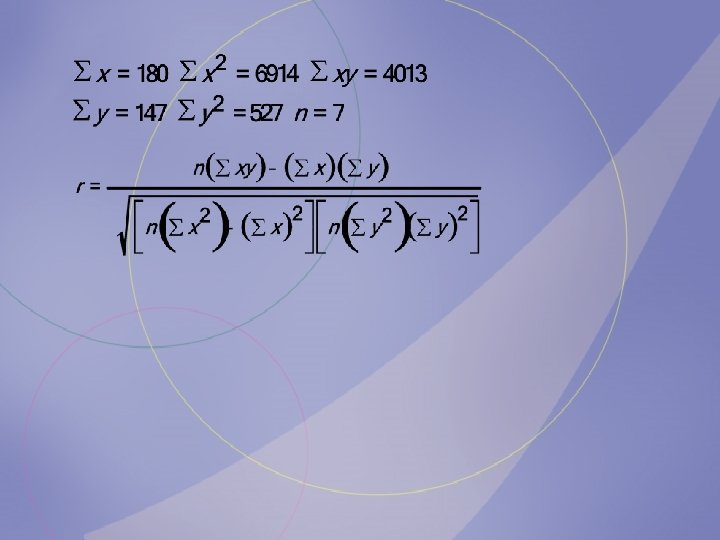


c. State the hypotheses. Number of larceny crimes, x 24 6 1 64 10 25 35 6 Number of vandalism crimes y 21 3 6 15 21 61 20

d. Test the significance of the correlation coefficient at = 0. 05, using Table I. Number of larceny crimes, x 24 6 1 64 10 25 35 6 Number of vandalism crimes y 21 3 6 15 21 61 20

e. Give a brief explanation of the type of relationship. Number of larceny crimes, x 24 6 1 64 10 25 35 6 Number of vandalism crimes y 21 3 6 15 21 61 20 There is not a significant linear relationship between the number of larceny crimes and the number of vandalism crimes.

Chapter 10 Correlation and Regression Section 103 Exercise #23

For the following exercise, complete these steps. a. Draw the scatter plot for the variables. b. Compute the value of the correlation coefficient. c. State the hypotheses. d. Test the significance of the correlation coefficient at = 0. 05, using Table I. e. Give a brief explanation of the type of relationship.

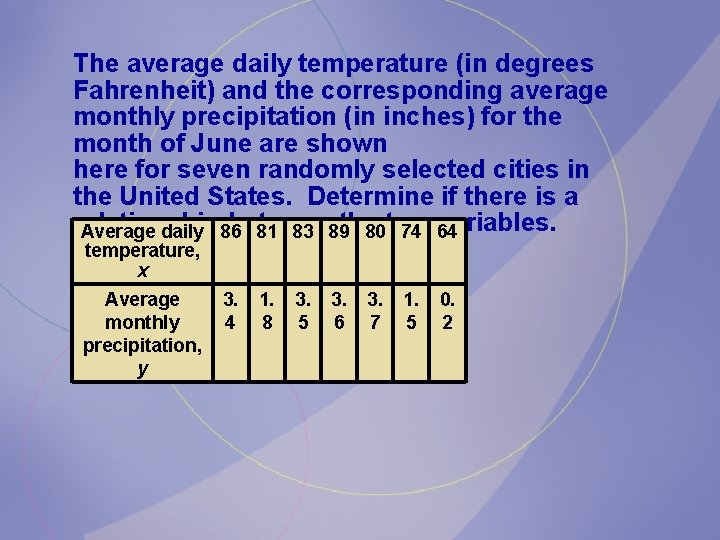
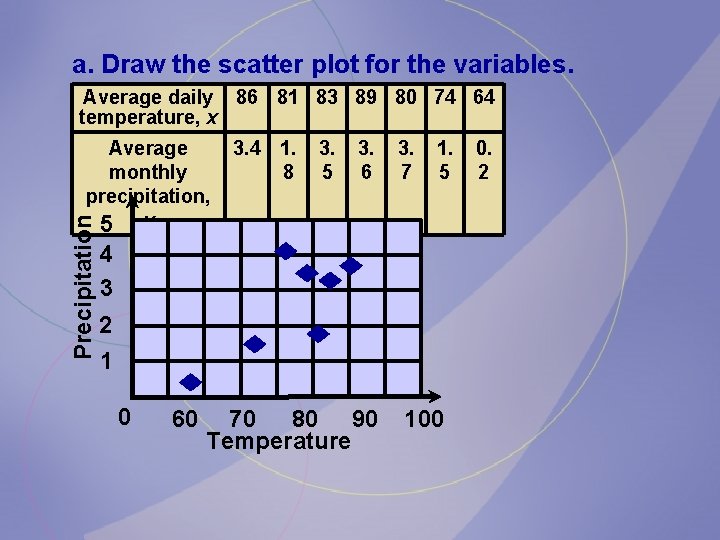
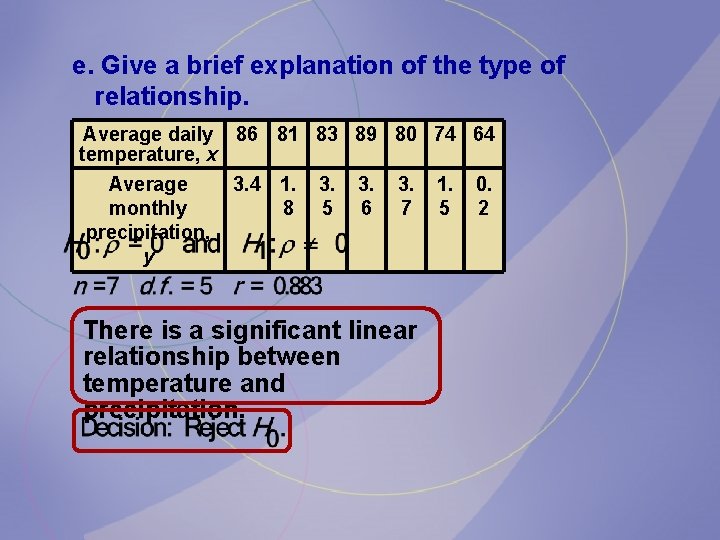
The average daily temperature (in degrees Fahrenheit) and the corresponding average monthly precipitation (in inches) for the month of June are shown here for seven randomly selected cities in the United States. Determine if there is a relationship between the Average daily 86 81 83 89 80 two 74 variables. 64 temperature, x Average monthly precipitation, y 3. 4 1. 8 3. 5 3. 6 3. 7 1. 5 0. 2

a. Draw the scatter plot for the variables. Average daily 86 81 83 89 80 74 64 temperature, x Precipitation Average monthly precipitation, 5 y 3. 4 1. 8 3. 5 3. 6 3. 7 1. 5 4 3 2 1 0 60 70 80 90 Temperature 100 0. 2

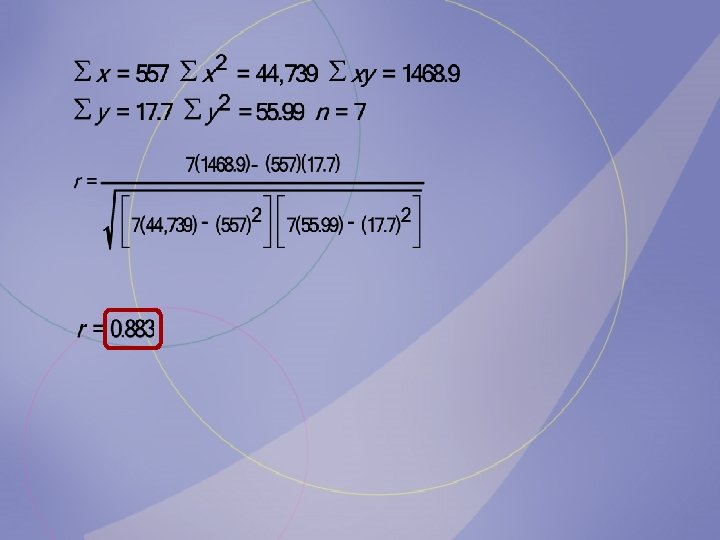
b. Compute the value of the correlation coefficient. Average daily 86 81 83 89 80 74 64 temperature, x Average monthly precipitation, y 3. 4 1. 8 3. 5 3. 6 3. 7 1. 5 0. 2
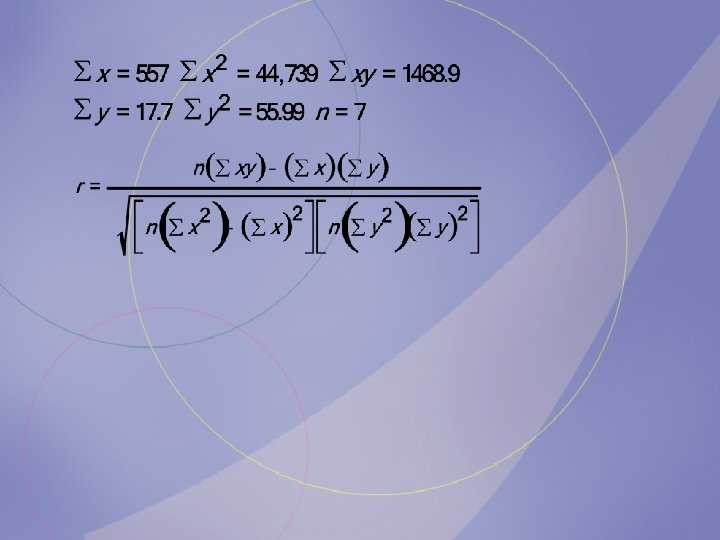


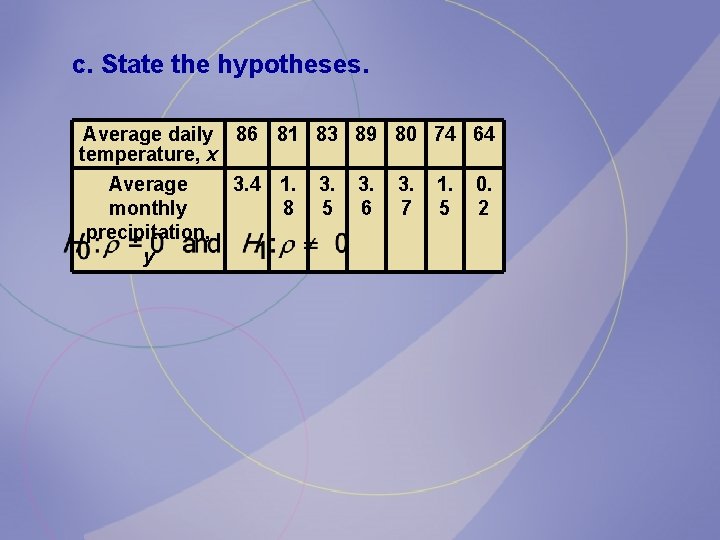
c. State the hypotheses. Average daily 86 81 83 89 80 74 64 temperature, x Average monthly precipitation, y 3. 4 1. 8 3. 5 3. 6 3. 7 1. 5 0. 2

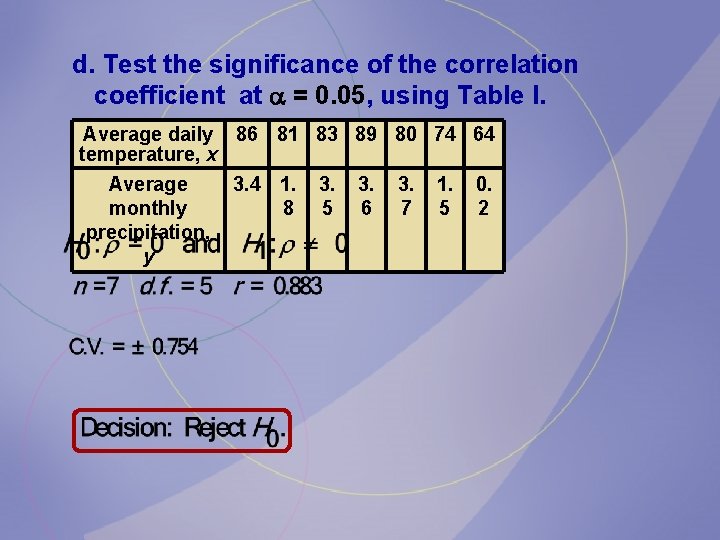
d. Test the significance of the correlation coefficient at = 0. 05, using Table I. Average daily 86 81 83 89 80 74 64 temperature, x Average monthly precipitation, y 3. 4 1. 8 3. 5 3. 6 3. 7 1. 5 0. 2

e. Give a brief explanation of the type of relationship. Average daily 86 81 83 89 80 74 64 temperature, x Average monthly precipitation, y 3. 4 1. 8 3. 5 3. 6 3. 7 There is a significant linear relationship between temperature and precipitation. 1. 5 0. 2

Chapter 10 Correlation and Regression Section 104 Regression

Chapter 10 Correlation and Regression Section 104 Exercise #13

Find the equation of the regression line and find the y value for the specified x value. Remember that no regression should be done when r is not significant. Ages and Exercise Age x 18 26 32 38 52 59 Hours y 10 5 2 3 1. 1 5
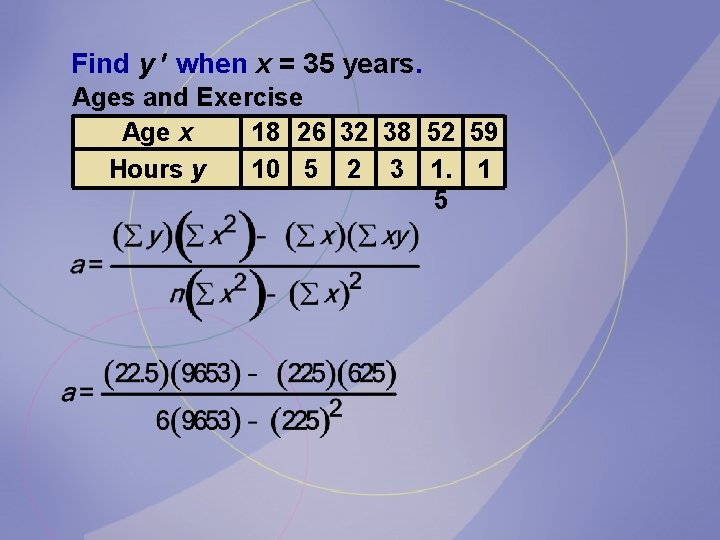
Find y when x = 35 years. Ages and Exercise Age x 18 26 32 38 52 59 Hours y 10 5 2 3 1. 1 5
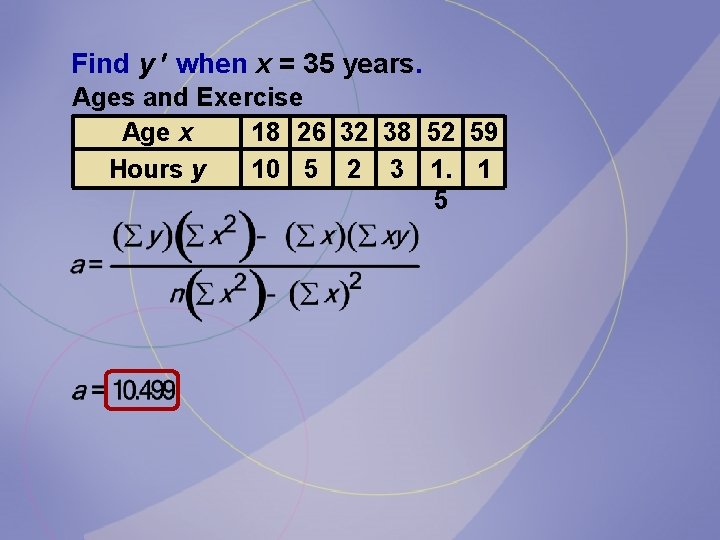
Find y when x = 35 years. Ages and Exercise Age x 18 26 32 38 52 59 Hours y 10 5 2 3 1. 1 5
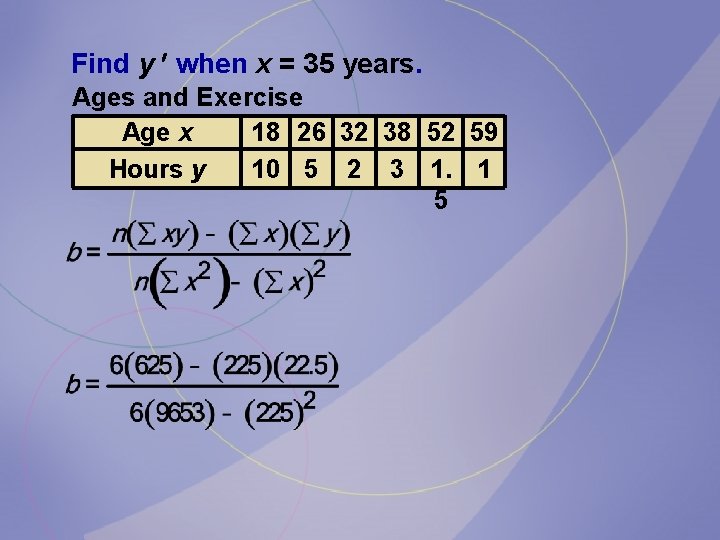
Find y when x = 35 years. Ages and Exercise Age x 18 26 32 38 52 59 Hours y 10 5 2 3 1. 1 5
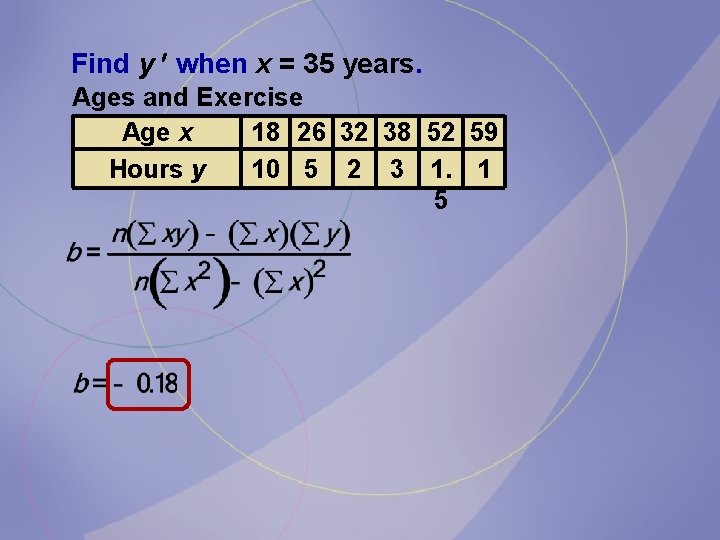
Find y when x = 35 years. Ages and Exercise Age x 18 26 32 38 52 59 Hours y 10 5 2 3 1. 1 5

Find y when x = 35 years. Ages and Exercise Age x 18 26 32 38 52 59 Hours y 10 5 2 3 1. 1 5

Chapter 10 Correlation and Regression Section 104 Exercise #15

Find the equation of the regression line and find the y value for the specified x value. Remember that no regression should be done when rand is not significant. Years Contribution Years x 1 Contribution y, $ 500 5 3 10 7 6 100 300 50 75 80

Find y when x = 4 years. Years and Contribution Years x 1 Contribution y, $ 500 5 3 10 7 6 100 300 50 75 80


Find y when x = 4 years. Years and Contribution Years x 1 Contribution y, $ 500 5 3 10 7 6 100 300 50 75 80


Find y when x = 4 years. Years and Contribution Years x 1 Contribution y, $ 500 5 3 10 7 6 100 300 50 75 80

Chapter 10 Correlation and Regression Section 104 Exercise #23

Find the equation of the regression line and find the y value when x = 70 ºF. Remember that no regression should be done when r is not significant. ( in. F ) and precipitation (in. ) Temperatures Avg. daily temp. x Avg. mo. Precip. y 86 81 83 89 80 74 64 3. 4 1. 8 3. 5 3. 6 3. 7 1. 5 0. 2




Chapter 10 Correlation and Regression Section 105 Coefficient of Determination and Standard Error of the Estimate

Chapter 10 Correlation and Regression Section 105 Exercise #9

Find the coefficients of determination and nondetermination when and explain the meaning of: 49% of the variation of y is due to the variation of x.

Find the coefficients of determination and nondetermination when and explain the meaning of: 51% of the variation of y is due to chance.

Chapter 10 Correlation and Regression Section 105 Exercise #15

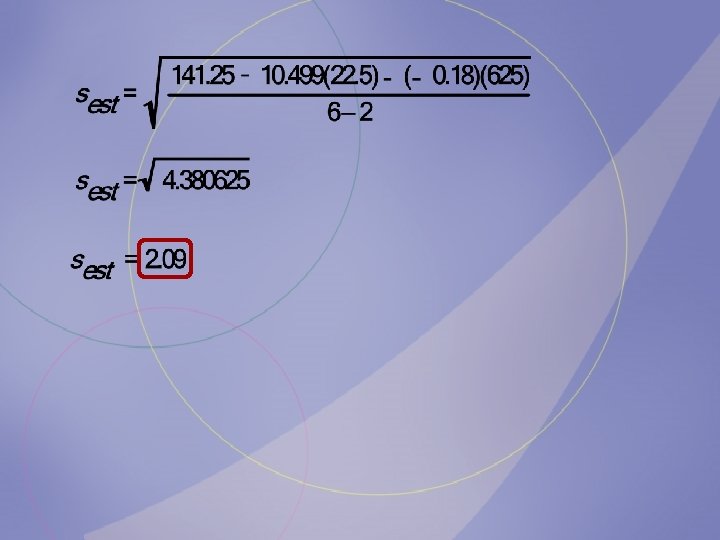
Compute the standard error of the estimate.


Chapter 10 Correlation and Regression Section 105 Exercise #19

Find the 90% prediction interval when x = 20 years. Age x 18 26 32 38 52 59 Hours y 10 5 2 3 1. 5 1



Chapter 10 Correlation and Regression Section 105 Exercise #21

Find the 90% prediction interval when x = 4 years. Years x 1 5 3 10 7 6 Contributions y, $ 50 0 10 0 30 0 50 75 80



Chapter 10 Correlation and Regression Section 106 Multiple Regression

Chapter 10 Correlation and Regression Section 106 Exercise #7

A manufacturer found that a significant relationship exists among the number of hours an assembly line employee works per shift x 1, the total number of items produced x 2, and the number of defective items produced y. The multiple regression equation is. Predict the number of defective items produced by an employee who has worked 9 hours and produced 24 items.


Chapter 10 Correlation and Regression Section 106 Exercise #9

An educator has found a significant relationship among a college graduate’s IQ x 1, score on the verbal section of the SAT x 2, and income for the first year following graduation from college y. Predict the income of a college graduate whose IQ is 120 and verbal SAT score is 650. The regression equation is