Chapter 10 Conic Sections 10 1 The Parabola

Chapter 10 Conic Sections 10. 1 – The Parabola and the Circle 10. 2 – The Ellipse 10. 3 – The Hyperbola 10. 4 – Nonlinear Systems of Equations and Their Applications

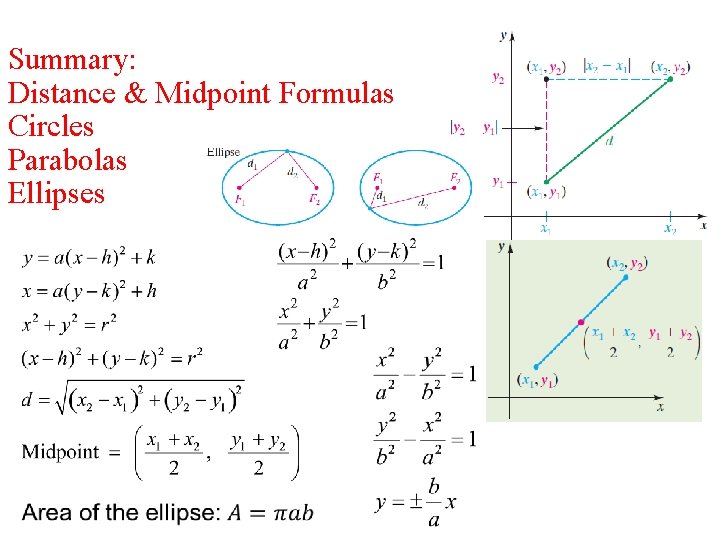
Summary: Distance & Midpoint Formulas Circles Parabolas Ellipses

10. 4 Nonlinear Systems of Equations and Their Applications • 1. Solve nonlinear systems of equations using substitution. • 2. Solve nonlinear systems of equations using elimination.

Nonlinear System of Equations A nonlinear system of equations is a system of equations in which at least one equation is not linear, that is, one whose graph is not a straight line. No points of intersection: no solutions One point of intersection: Two points of One solution intersection: two solutions

Solve Nonlinear Systems Using Substitution Example 1: Solve x 2 + y 2 = 20, (1) (a circle. ) y – 2 x = 0. (a line. ) (2) Solution Solve the second equation for y: y = 2 x. (3) x 2 + (2 x)2 = 20 x 2 + 4 x 2 = 20 5 x 2 = 20 x 2 = 4 Now substitute these numbers for x in equation (3) and solve for y: The solutions are: (2, 4) & (– 2, – 4).

Solve Nonlinear Systems Using Elimination (Addition) Example 2: Solve. 3 x 2 + 2 y 2 x 2 – y 2 = 7. = 66 2 x 2 – 2 y 2 = 14 5 x 2 3 x 2 + 2 y 2 = 66, (1) = 80 x 2 = 16 x = ( )2 – y 2 = 7 16 – y 2 = 7 –y 2 = – 9 y 2 = 9 y=. The system has four solutions: (4, 3), (4, – 3), (– 4, 3), and (– 4, – 3). (2)

Solve Nonlinear Systems Using Elimination (Addition) Example 3: Solve the system of equations. Solution The solutions are

Solve Nonlinear Systems Using Substitution Example 4: Solve the system of equations.

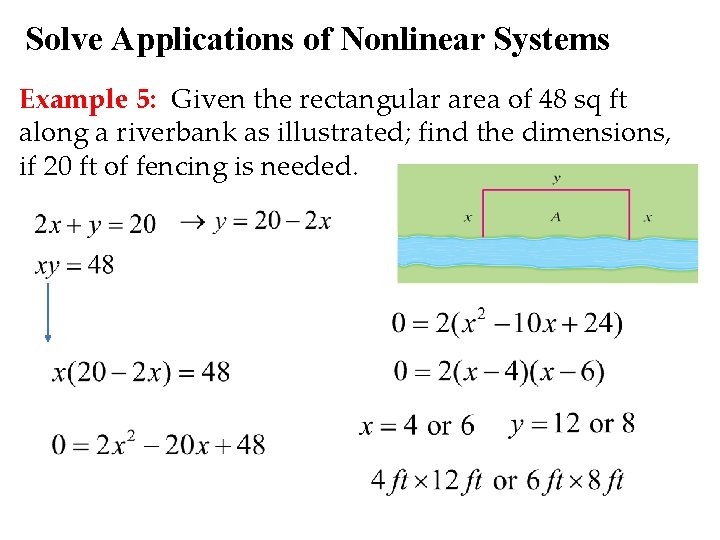
Solve Applications of Nonlinear Systems Example 5: Given the rectangular area of 48 sq ft along a riverbank as illustrated; find the dimensions, if 20 ft of fencing is needed.

Solve Applications of Nonlinear Systems Example 6: Q 48 C=15 a b

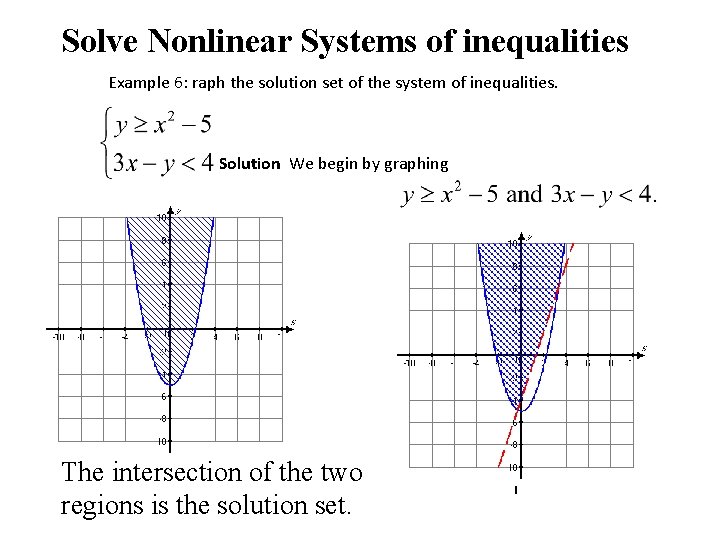
Solve Nonlinear Systems of inequalities Example 6: raph the solution set of the system of inequalities. Solution We begin by graphing The intersection of the two regions is the solution set.