Chapter 10 Congruent and Similar Triangles Introduction Recognizing

Chapter 10 Congruent and Similar Triangles

Introduction Recognizing and using congruent and similar shapes can make calculations and design work easier. For instance, in the design at the corner, only two different shapes were actually drawn. The design was put together by copying and manipulating these shapes to produce versions of them of different sizes and in different positions. In this chapter, we will look in a little more depth at the mathematical meaning of the terms similar and congruent, which describe the relation between shapes like those in design.

Similar and Congruent Figures • Congruent polygons have all sides congruent and all angles congruent. • Similar polygons have the same shape; they may or may not have the same size. Worksheet : Exercise 1 : Which of the following pairs are congruent and which are similar?

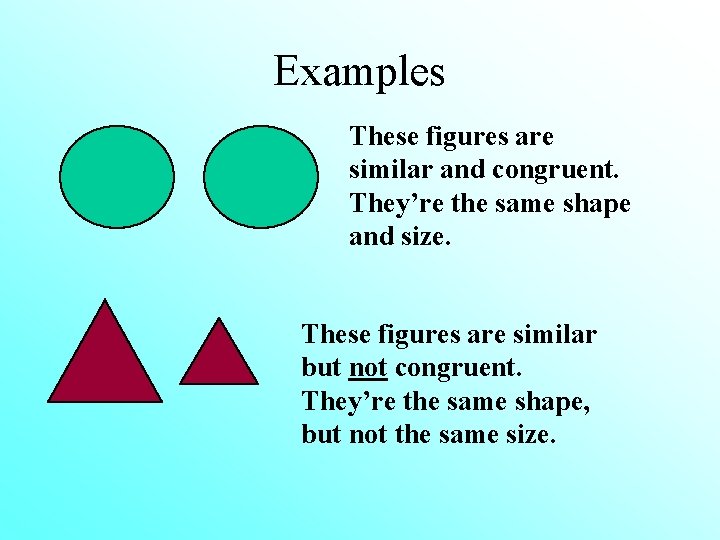
Examples These figures are similar and congruent. They’re the same shape and size. These figures are similar but not congruent. They’re the same shape, but not the same size.

Another Example These figures are neither similar nor congruent. They’re not the same shape or the same size. Even though they’re both triangles, they’re not similar because they’re not the same shape triangle. Note: Two figures can be similar but not congruent, but they can’t be congruent but not similar. Think about why!

Congruent Figures When 2 figures are congruent, i. e. 2 figures have the same shape and size, §Corresponding angles are equal §Corresponding sides are equal §Symbol :

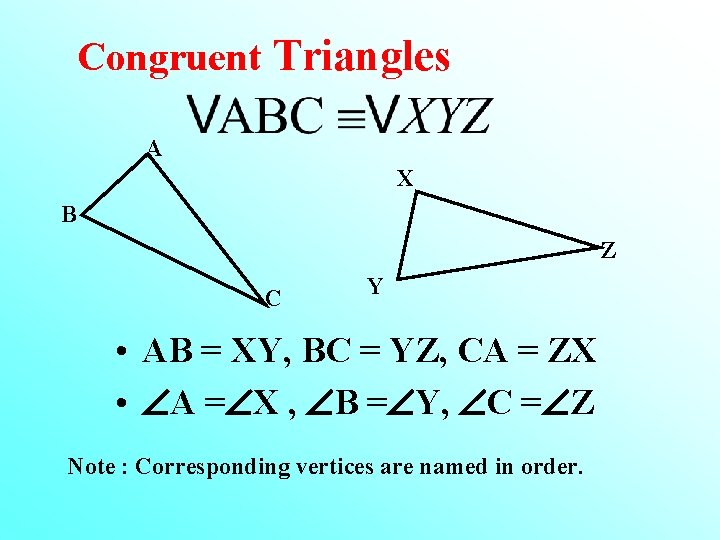
Congruent Triangles A X B Z C Y • AB = XY, BC = YZ, CA = ZX • A = X , B = Y, C = Z Note : Corresponding vertices are named in order.

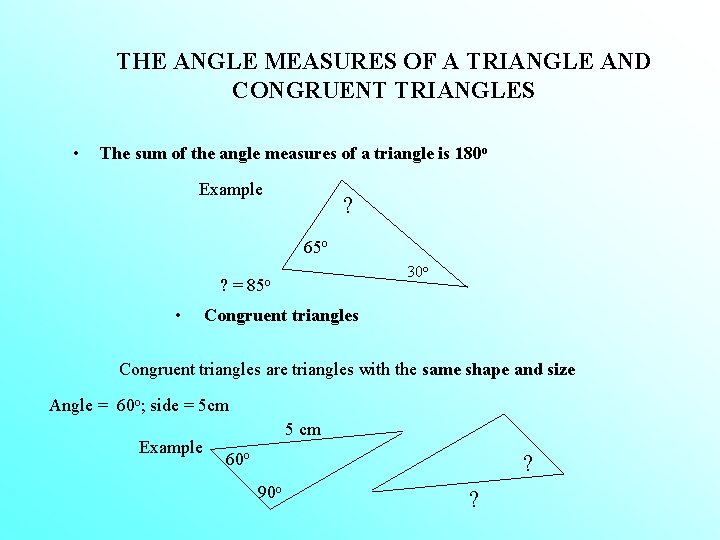
THE ANGLE MEASURES OF A TRIANGLE AND CONGRUENT TRIANGLES • The sum of the angle measures of a triangle is 180 o Example ? 65 o ? = • 30 o 85 o Congruent triangles are triangles with the same shape and size Angle = 60 o; side = 5 cm Example 5 cm 60 o ? 90 o ?

Isosceles triangles • An isosceles triangle is the triangle which has at least two sides with the same length • In an isosceles triangle, angles that are opposite the equal-length sides have the same measure ? Example 82 cm ? 52 o The side = 82 cm, the angle = 76 o

Equilateral triangles • An equilateral triangle has three sides of equal length • In an equilateral triangle, the measure of each angle is 60 o Example 60 o 100 cm ? ? Angle = 60 o, side = 100 cm

Right triangles and Pythagorean theorem • A right triangle is the triangle with one right angle Hypotenuse c Leg • Pythagorean theorem b c 2 = a 2 + b 2 Leg Example a 60 o ? 3 cm ? 4 cm c 2 = 42 + 32 = 25 C=5

Ex 10 A Page 47 • Q 2 a • By comparing, x = 4. 8, y = 42 • Q 2 d • By comparing, x = 22, y = 39 – 22 = 17 • Q 2 b • By comparing, x = 16, y = 30 ( 180 - 75 )

Tests for Congruency Ways to prove triangles congruent : • SSS ( Side – Side ) • SAS ( Side – Angle – Side ) • ASA ( Angle – Side – Angle ) or AAS ( Angle – Side ) • RHS ( Right angle – Hypotenuse – Side )

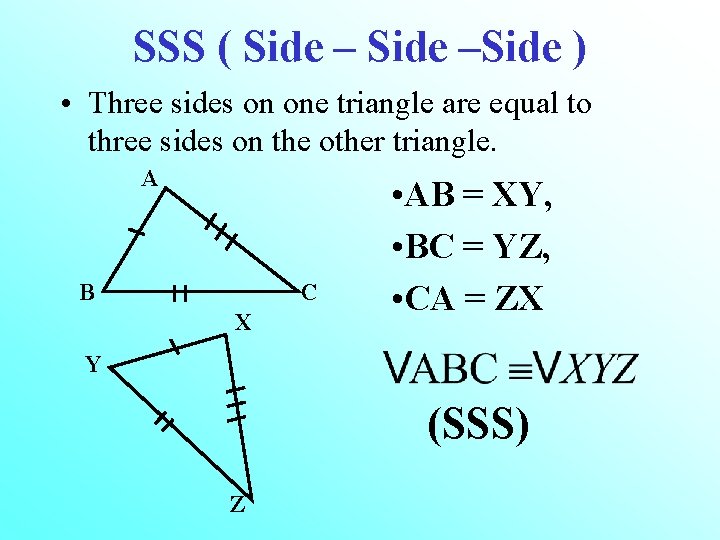
SSS ( Side –Side ) • Three sides on one triangle are equal to three sides on the other triangle. A B C X • AB = XY, • BC = YZ, • CA = ZX Y (SSS) Z

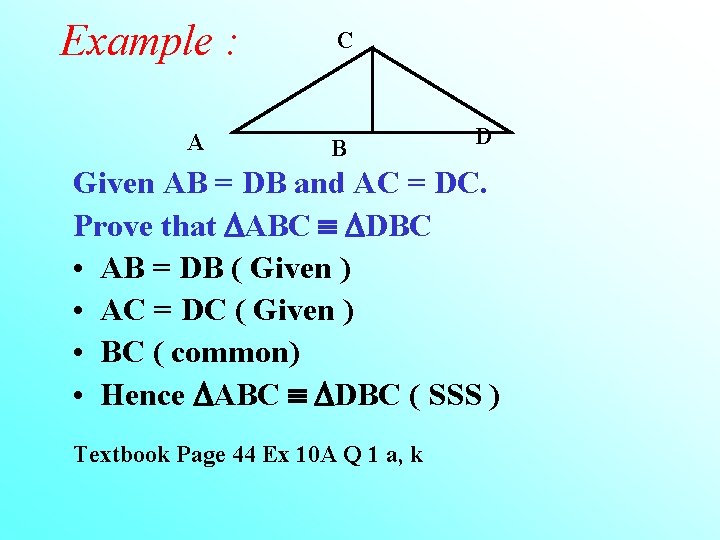
Example : A C B D Given AB = DB and AC = DC. Prove that ABC DBC • AB = DB ( Given ) • AC = DC ( Given ) • BC ( common) • Hence ABC DBC ( SSS ) Textbook Page 44 Ex 10 A Q 1 a, k

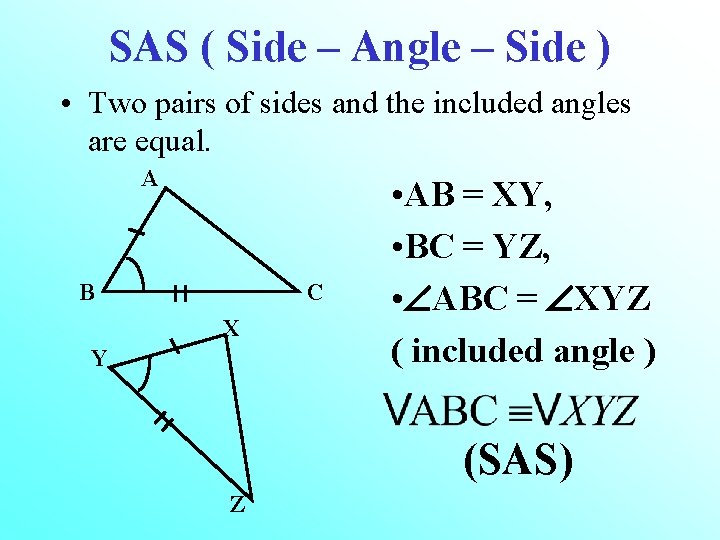
SAS ( Side – Angle – Side ) • Two pairs of sides and the included angles are equal. A B C X Y • AB = XY, • BC = YZ, • ABC = XYZ ( included angle ) (SAS) Z

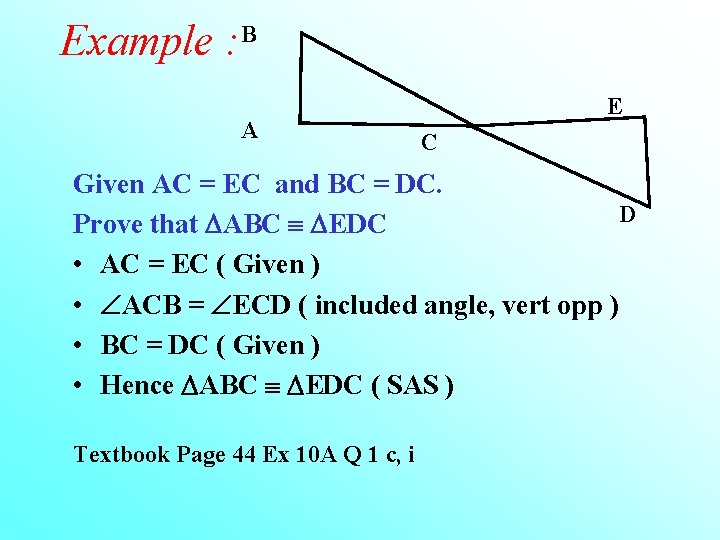
Example : B A E C Given AC = EC and BC = DC. D Prove that ABC EDC • AC = EC ( Given ) • ACB = ECD ( included angle, vert opp ) • BC = DC ( Given ) • Hence ABC EDC ( SAS ) Textbook Page 44 Ex 10 A Q 1 c, i

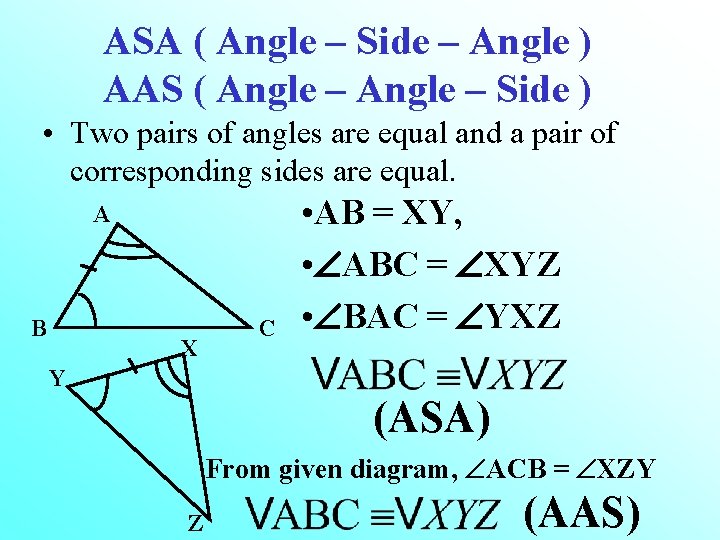
ASA ( Angle – Side – Angle ) AAS ( Angle – Side ) • Two pairs of angles are equal and a pair of corresponding sides are equal. A B X C • AB = XY, • ABC = XYZ • BAC = YXZ Y (ASA) From given diagram, ACB = XZY Z (AAS)

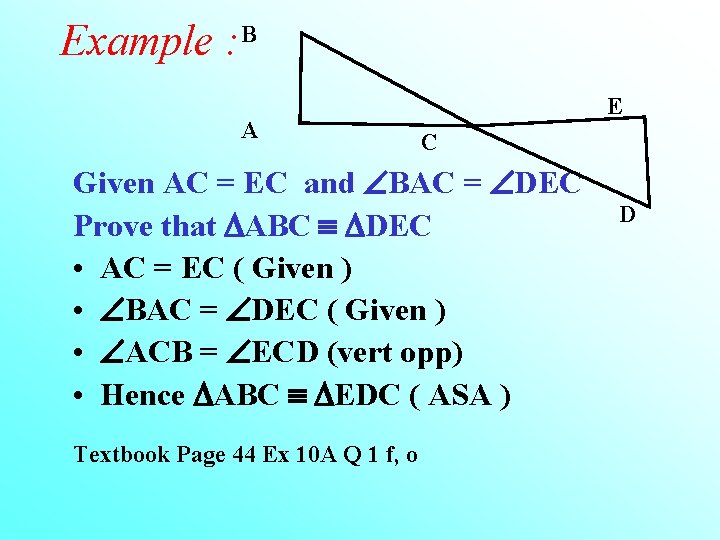
Example : B A E C Given AC = EC and BAC = DEC Prove that ABC DEC • AC = EC ( Given ) • BAC = DEC ( Given ) • ACB = ECD (vert opp) • Hence ABC EDC ( ASA ) Textbook Page 44 Ex 10 A Q 1 f, o D

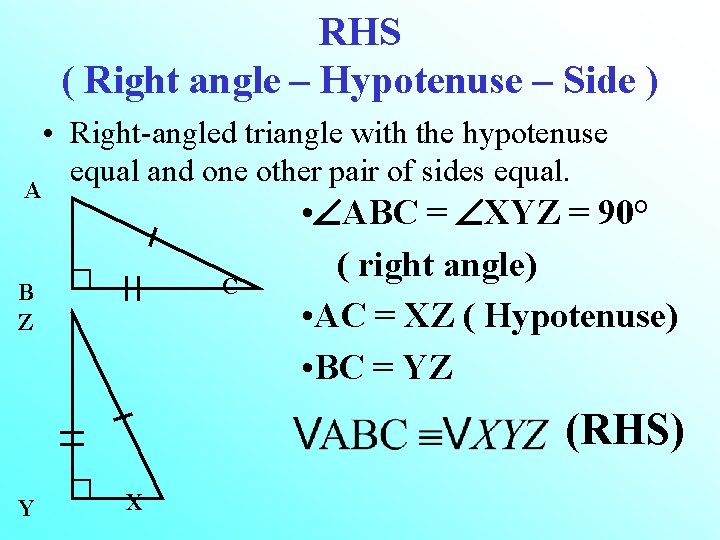
RHS ( Right angle – Hypotenuse – Side ) A • Right-angled triangle with the hypotenuse equal and one other pair of sides equal. C B Z • ABC = XYZ = 90° ( right angle) • AC = XZ ( Hypotenuse) • BC = YZ (RHS) Y X

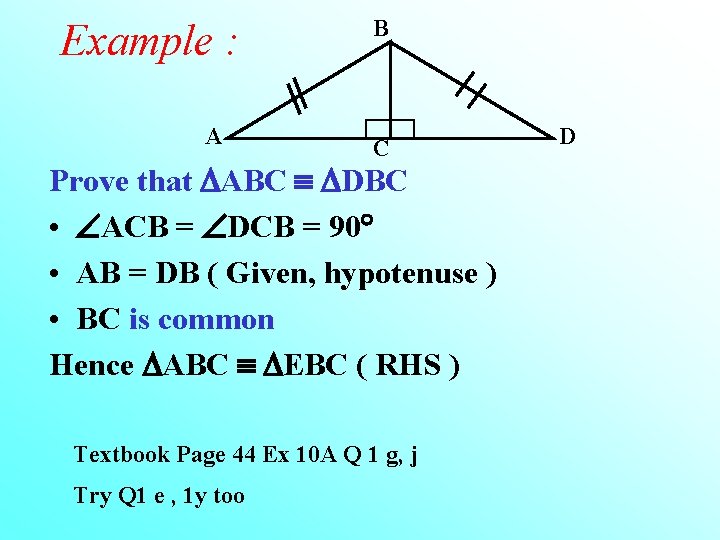
Example : A B C Prove that ABC DBC • ACB = DCB = 90 • AB = DB ( Given, hypotenuse ) • BC is common Hence ABC EBC ( RHS ) Textbook Page 44 Ex 10 A Q 1 g, j Try Q 1 e , 1 y too D

Time to work • • • Class Work Ex 10 B Pg 49 Q 1 Q 2 Q 4 Q 6 • • • Home Work Ex 10 A Page 44 -47 Q 1 b, h, m, p, r, x Q 2 c, e Ex 10 B Pg 49 -50 Q 3, 5, 7, 8

Thinking Time ? ? ? • If 3 angles on A are equal to the 3 corresponding angles on the other B, are the two triangles congruent ?

Ratios and Similar Figures • Similar figures have corresponding sides and corresponding angles that are located at the same place on the figures. • Corresponding sides have to have the same ratios between the two figures.

Ratios and Similar Figures A B Example C These sides correspond: AB and EF BD and FH CD and GH AC and EG D E F G H These angles correspond: A and E B and F D and H C and G

Ratios and Similar Figures 14 m 7 m Example 3 m These rectangles are similar, because the ratios of these corresponding sides are equal: 6 m

Proportions and Similar Figures • A proportion is an equation that states that two ratios are equivalent. • Examples: n=5 m=4

Proportions and Similar Figures You can use proportions of corresponding sides to figure out unknown lengths of sides of polygons. 16 m n 10 m 5 m 10/16 = 5/n so n = 8 m

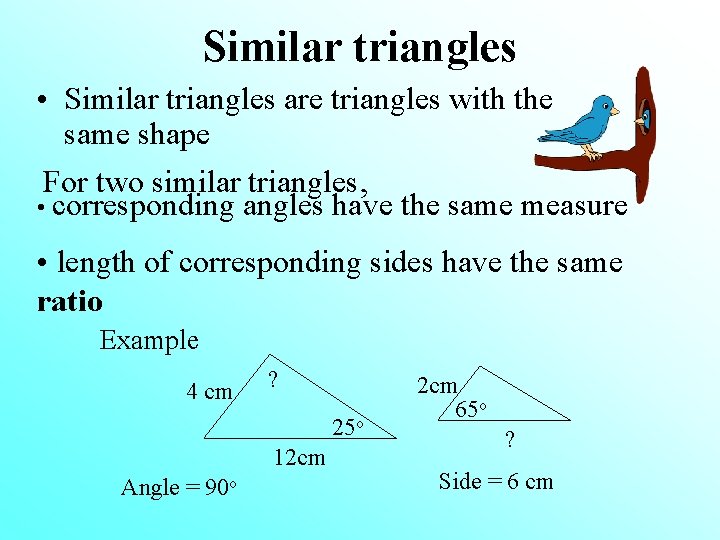
Similar triangles • Similar triangles are triangles with the same shape For two similar triangles, • corresponding angles have the same measure • length of corresponding sides have the same ratio Example 4 cm ? 25 o 12 cm Angle = 90 o 2 cm 65 o ? Side = 6 cm

Similar Triangles 3 Ways to Prove Triangles Similar

Similar triangles are like similar polygons. Their corresponding angles are CONGRUENT and their corresponding sides are PROPORTIONAL. 10 6 3 8 5 4

But you don’t need ALL that information to be able to tell that two triangles are similar….

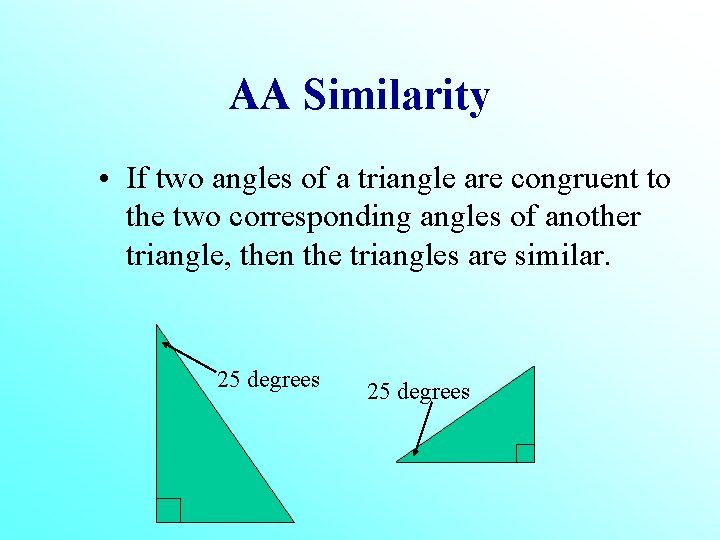
AA Similarity • If two angles of a triangle are congruent to the two corresponding angles of another triangle, then the triangles are similar. 25 degrees

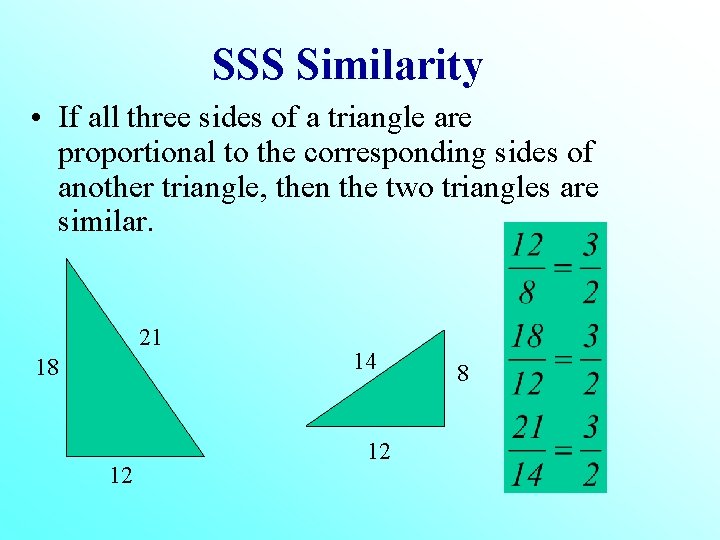
SSS Similarity • If all three sides of a triangle are proportional to the corresponding sides of another triangle, then the two triangles are similar. 21 18 12 14 12 8

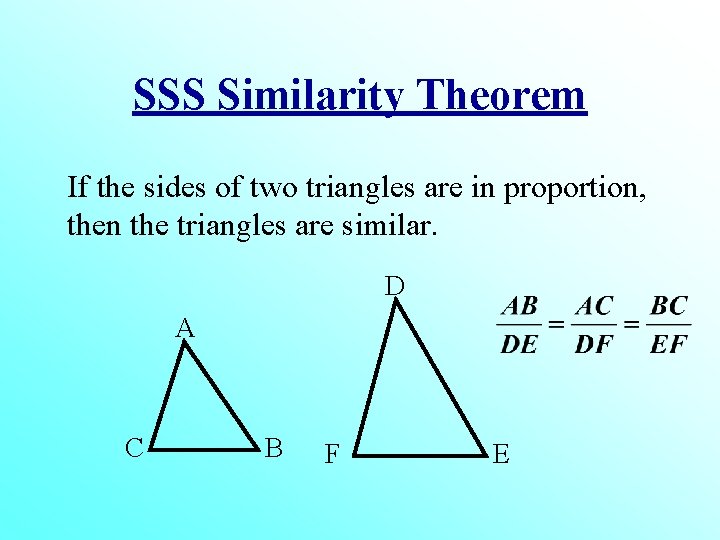
SSS Similarity Theorem If the sides of two triangles are in proportion, then the triangles are similar. D A C B F E

SAS Similarity • If two sides of a triangle are proportional to two corresponding sides of another triangle AND the angles between those sides are congruent, then the triangles are similar. 18 21 14 12

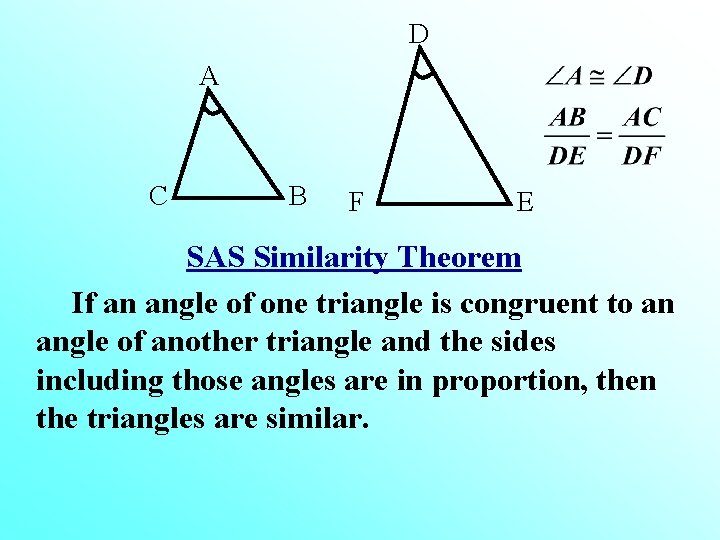
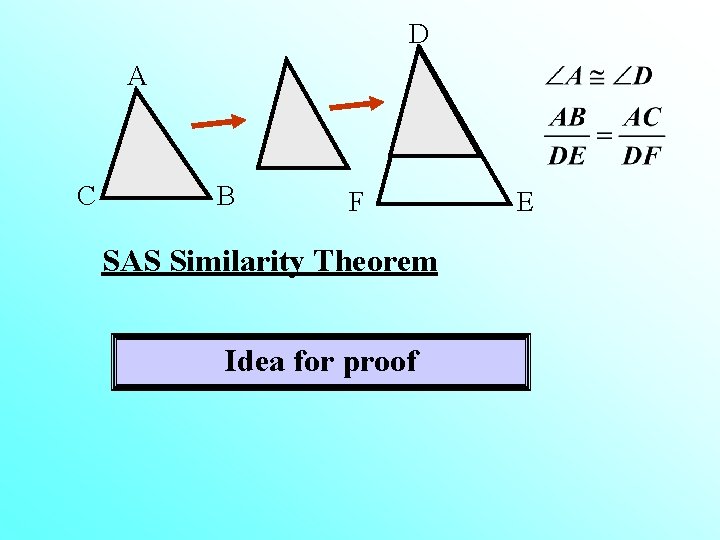
D A C B F E SAS Similarity Theorem If an angle of one triangle is congruent to an angle of another triangle and the sides including those angles are in proportion, then the triangles are similar.

D A C B F SAS Similarity Theorem Idea for proof E

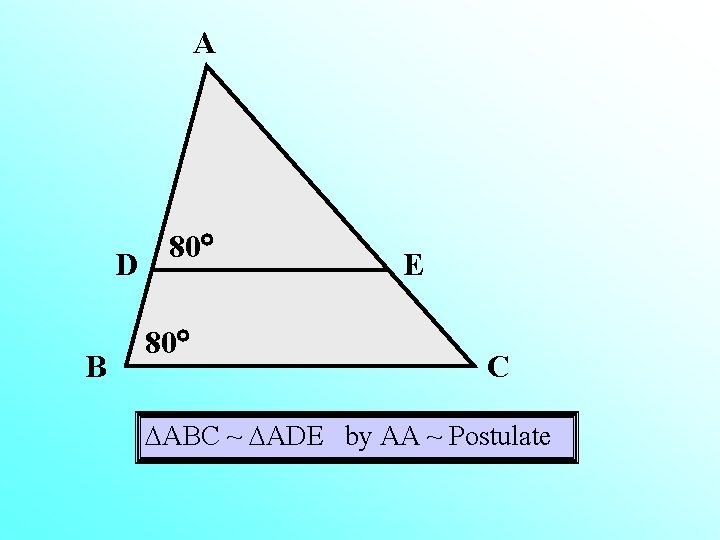
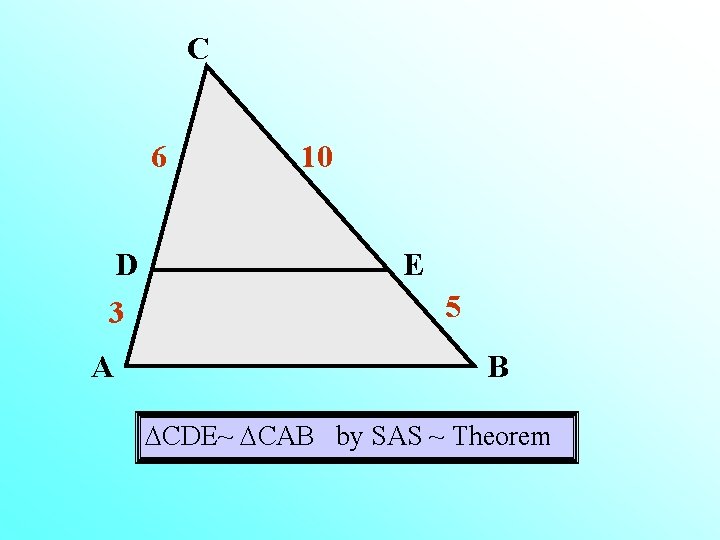
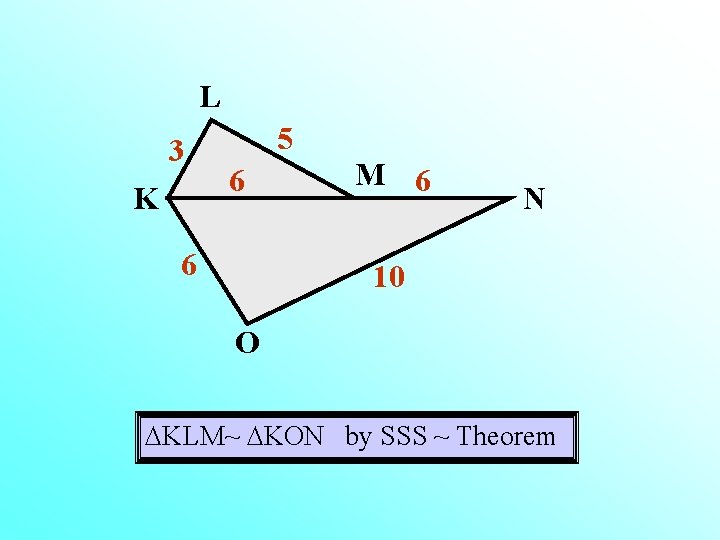
Name Similar Triangles and Justify Your Answer!

A D B 80 80 E C ABC ~ ADE by AA ~ Postulate

C 6 D 3 A 10 E 5 B CDE~ CAB by SAS ~ Theorem

L 3 K 5 6 6 M 6 N 10 O KLM~ KON by SSS ~ Theorem

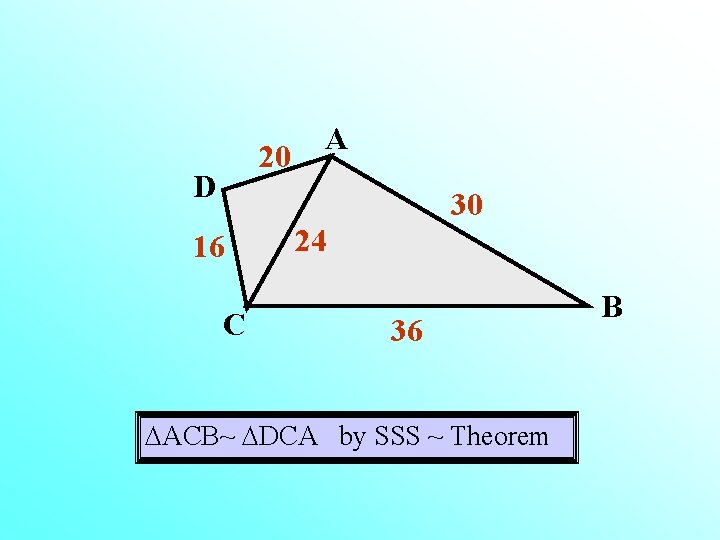
20 D A 30 16 C 24 36 ACB~ DCA by SSS ~ Theorem B

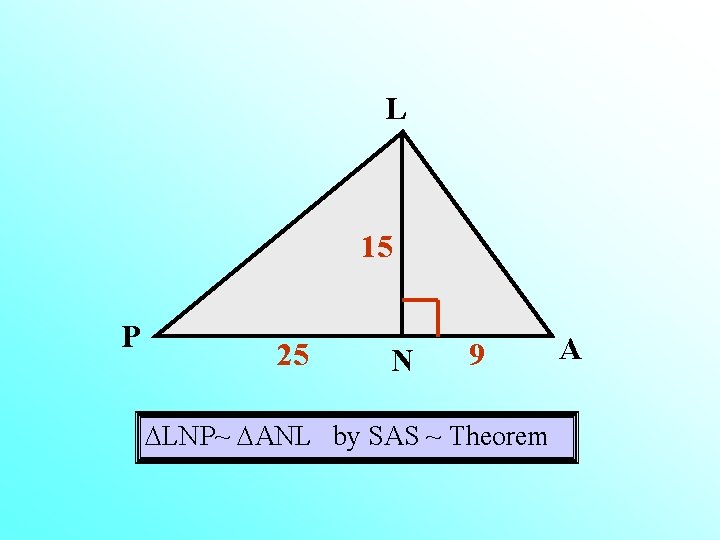
L 15 P 25 N 9 LNP~ ANL by SAS ~ Theorem A

Time to work !!!! o. Class work o. Home work Ex 10 C Page 54 §Q 2 a to h §Q 1 a to f §Q 3 §Q 4 §Q 5 §Q 7 §Q 6 a to d §Q 9 §Q 8 §Q 11 §Q 10 §Q 14 §Q 12 §Q 15 §Q 13

Areas of Similar Figures Activity : Complete the table for each of the given pairs of similar figures Conclusion: If the ratio of the corresponding lengths of two similar figures is then the ratio of their areas is

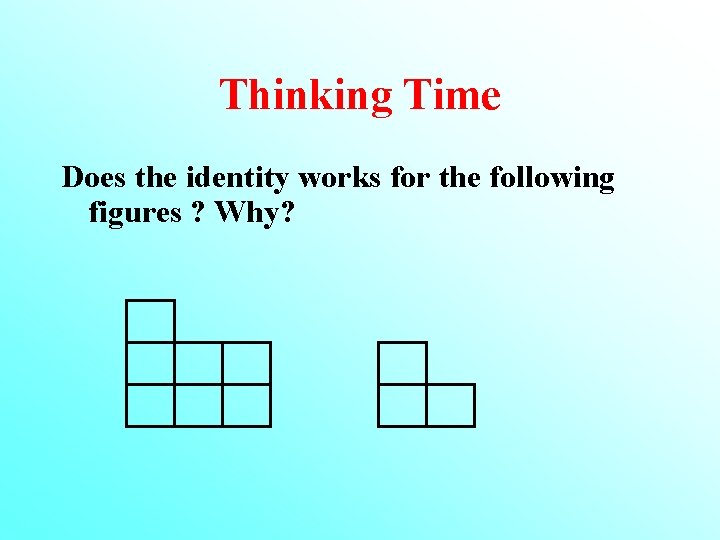
Thinking Time Does the identity works for the following figures ? Why?

Time to work !!! • • Class work Ex 10 D Pg 62 Q 1 a to d Q 3 Q 4 Q 5 Q 8 Q 9 • • Class work Ex 10 D Pg 62 Q 10 Q 12 Q 13 Q 15 Q 16 Q 20 - 22

Home Work Ex 10 D Pg 62 • Q 6 • Q 7 • Q 11 • Q 14 • Q 17 • Q 18

Volumes of Similar Solids Activity : Complete the table for each of the given pairs of similar Solids Conclusion: If the ratio of the corresponding lengths of two similar figures is then the ratio of their volumes is

Total Surface Area of similar solids If the ratio of the corresponding lengths of two similar figures is then the ratio of their total surface areas is

Time to work • • Class work Ex 10 E Pg 67 Q 1 Q 2 Q 3 Q 4 Q 5 • • • Class work Ex 10 E Pg 67 Q 6 Q 9 Q 11

Q 3 ? How to find the weight of a similar solid? ? ? • If both solids were made from the same material, • Density will be the same • Hence using the formula : Density = Mass Volume

Your favourite moment • • Home work Ex 10 E Pg 67 Q 8 Q 10 Q 12 Q 13 Q 14