Chapter 10 Computer Arithmetic http sslab cnu ac

Chapter 10 Computer Arithmetic 충남대학교 컴퓨터전공 http: //sslab. cnu. ac. kr 이철훈 1

Chapter 10 Introduction n Arithmetic instructions manipulate date to produce results necessary for the solution of computational problems n 4가지 기본 arithmetic operations - n addition, subtraction, multiplication, and division Data types - Fixed-point binary data in signed-magnitude representation - Fixed-point binary data in signed-2’s compliment representation - Floating-point binary data - Binary-coded decimal (BCD) data Computer System Architecture 1 2

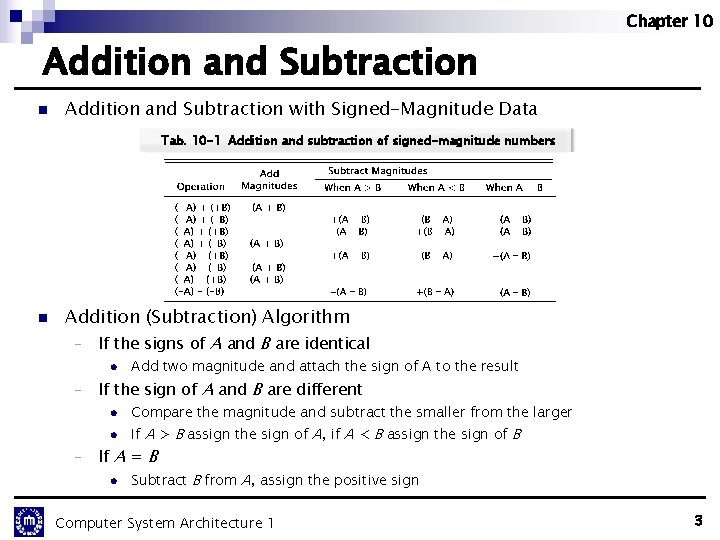
Chapter 10 Addition and Subtraction n Addition and Subtraction with Signed-Magnitude Data Tab. 10 -1 Addition and subtraction of signed-magnitude numbers n Addition (Subtraction) Algorithm - If the signs of A and B are identical l - If the sign of A and B are different l l - Add two magnitude and attach the sign of A to the result Compare the magnitude and subtract the smaller from the larger If A > B assign the sign of A, if A < B assign the sign of B If A = B l Subtract B from A, assign the positive sign Computer System Architecture 1 3

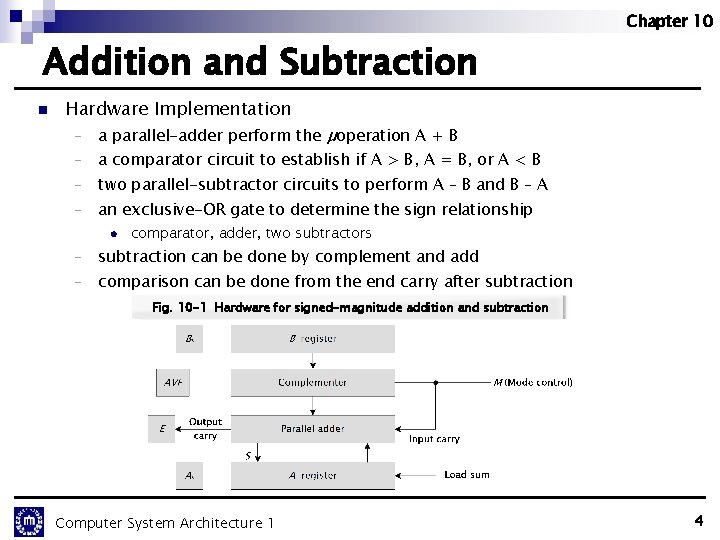
Chapter 10 Addition and Subtraction n Hardware Implementation - a parallel-adder perform the µoperation A + B - a comparator circuit to establish if A > B, A = B, or A < B - two parallel-subtractor circuits to perform A – B and B – A - an exclusive-OR gate to determine the sign relationship l comparator, adder, two subtractors - subtraction can be done by complement and add - comparison can be done from the end carry after subtraction Fig. 10 -1 Hardware for signed-magnitude addition and subtraction Computer System Architecture 1 4

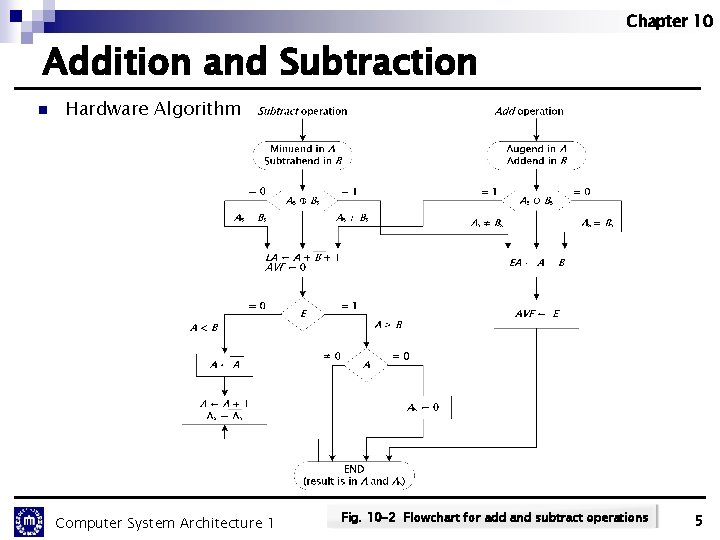
Chapter 10 Addition and Subtraction n Hardware Algorithm Computer System Architecture 1 Fig. 10 -2 Flowchart for add and subtract operations 5

Chapter 10 Addition and Subtraction n Addition (Subtraction) with Signed-2’s complement Data Fig. 10 -3 Hardware for signed-2’s complement addition and subtraction Computer System Architecture 1 Fig. 10 -4 Algorithm for adding and subtracting signed-2’s complement data 6

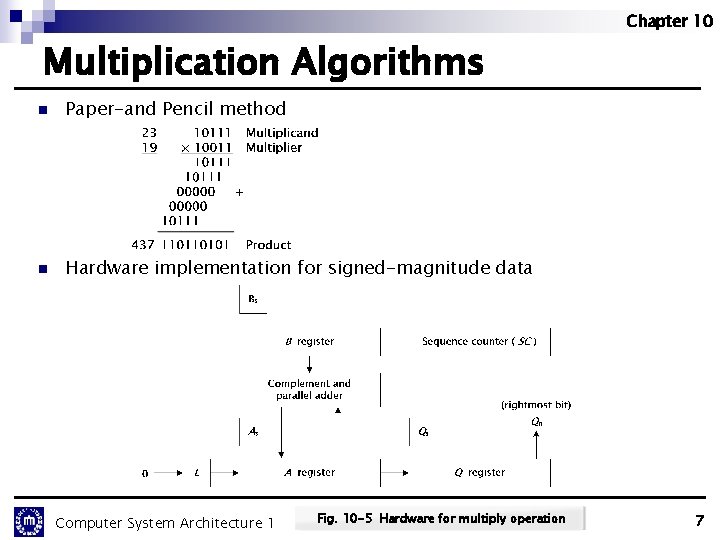
Chapter 10 Multiplication Algorithms n Paper-and Pencil method n Hardware implementation for signed-magnitude data Computer System Architecture 1 Fig. 10 -5 Hardware for multiply operation 7

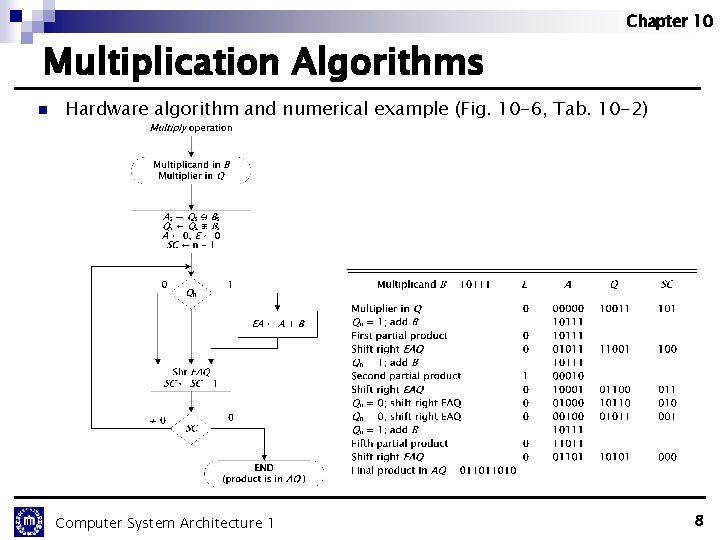
Chapter 10 Multiplication Algorithms n Hardware algorithm and numerical example (Fig. 10 -6, Tab. 10 -2) Computer System Architecture 1 8

Chapter 10 Multiplication Algorithms n Booth Multiply Algorithm - 1. 2. 3. multiplication with signed-2’s complement data string of 0’s in the multiplier require no addition but just shifting a string of 1’s from bit weight 2 k to weight 2 m ⇒ 2 k+1 – 2 m ⇒ 001110 (+14) = 24 -21 = 16 – 2 = 14 the multiplicand is subtracted from the partial product upon encountering the first least significant 1 in a string of 1’s in multiplier the multiplicand is added to the partial product upon encountering the first 0 in a string of 0’s in the multiplier the partial product does not change when the multiplier bit is identical to the previous multiplier bit Computer System Architecture 1 Fig. 10 -7 Hardware for Booth algorithm 9

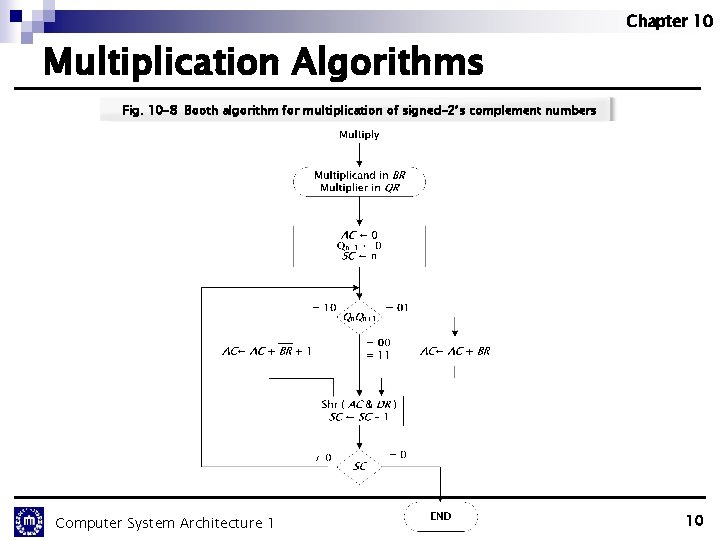
Chapter 10 Multiplication Algorithms Fig. 10 -8 Booth algorithm for multiplication of signed-2’s complement numbers Computer System Architecture 1 10

Chapter 10 Multiplication Algorithms n Example of Booth algorithm Tab. 10 -3 Example of multiplication with Booth algorithm n Combinational Array Multiplier - Sequential multiplier : need n steps The multiplication can be done with one step by means of a combinational circuit that forms the product bits all at once Requires a large number of gates (j multiplier bits, k multiplicand) l - ( j ∗ k ) AND gates, ( j - 1) k-bit adders 2 -bit by 2 -bit array multiplier Computer System Architecture 1 11

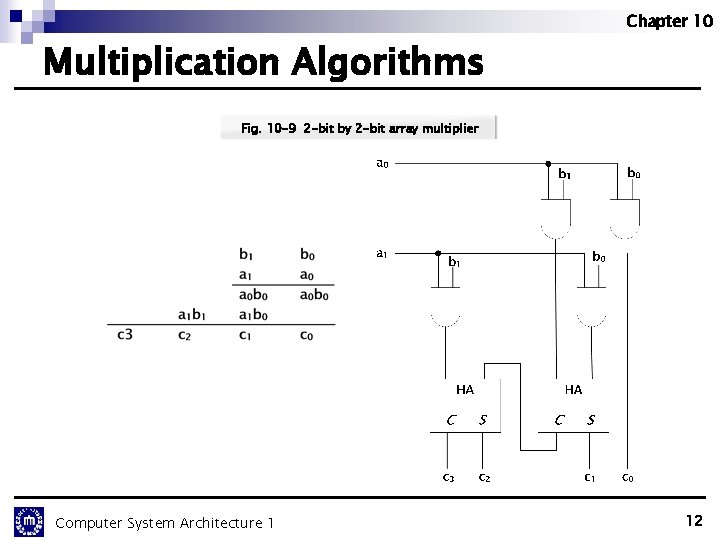
Chapter 10 Multiplication Algorithms Fig. 10 -9 2 -bit by 2 -bit array multiplier Computer System Architecture 1 12

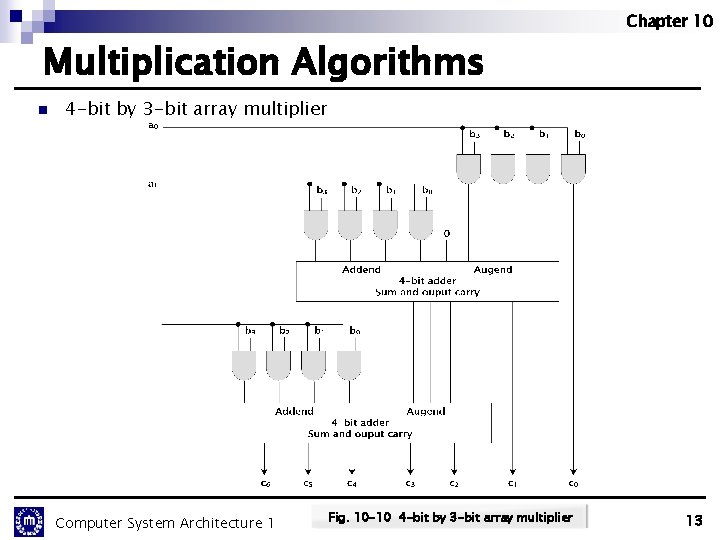
Chapter 10 Multiplication Algorithms n 4 -bit by 3 -bit array multiplier Computer System Architecture 1 Fig. 10 -10 4 -bit by 3 -bit array multiplier 13

Chapter 10 Division Algorithms n n Compare, Shift, Subtract operations Paper-and Pencil method Fig. 10 -11 Example of binary division n Hardware implementation for signed-magnitude data - If E = 1, A ≥ B l ⇒ quotient bit 1 is inserted into Qn, shift left the partial remainder l ⇒ Qn = 0, B is added to restore A to its previous value If E = 0, A < B Divide-overflow condition occurs if the high-order half bits of the dividend constitute a number greater than or equal to dividor (DVF) - Division-by-zero - Computer System Architecture 1 14

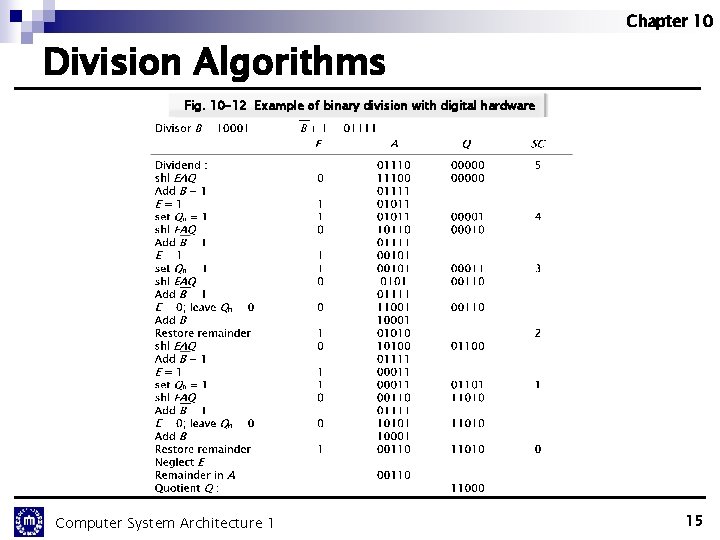
Chapter 10 Division Algorithms Fig. 10 -12 Example of binary division with digital hardware Computer System Architecture 1 15

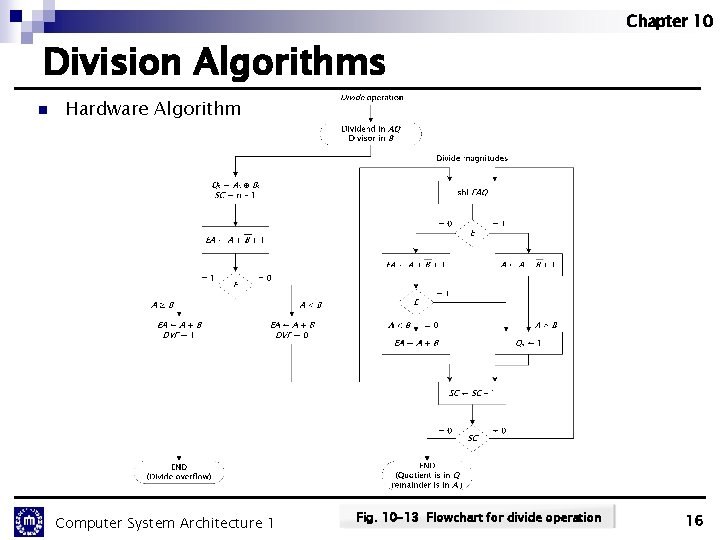
Chapter 10 Division Algorithms n Hardware Algorithm Computer System Architecture 1 Fig. 10 -13 Flowchart for divide operation 16