Chapter 10 ChiSquare Tests and the FDistribution Copyright

Chapter Outline • • . 10. 1 Goodness of Fit 10. 2 Independence 10.

Section 10. 2 Independence . Copyright © 2015, 2012, and 2009 Pearson Education, Inc.

Section 10. 2 Objectives • How to use a contingency table to find expected frequencies • How to use a chi-square distribution to test whether two variables are independent . Copyright © 2015, 2012, and 2009 Pearson Education, Inc. 4

Contingency Tables r × c contingency table • Shows the observed frequencies for two variables. • The observed frequencies are arranged in r rows and c columns. • The intersection of a row and a column is called a cell. . Copyright © 2015, 2012, and 2009 Pearson Education, Inc. 5

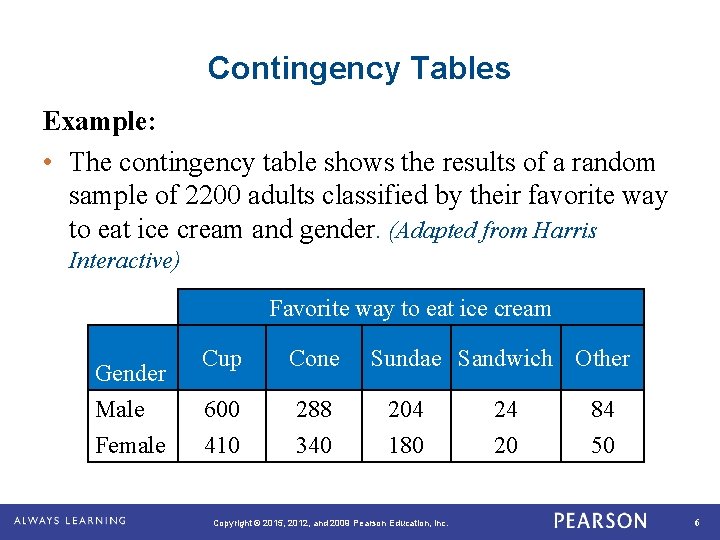
Contingency Tables Example: • The contingency table shows the results of a random sample of 2200 adults classified by their favorite way to eat ice cream and gender. (Adapted from Harris Interactive) Favorite way to eat ice cream Cup Cone Male 600 288 204 24 84 Female 410 340 180 20 50 Gender . Sundae Sandwich Other Copyright © 2015, 2012, and 2009 Pearson Education, Inc. 6

Finding the Expected Frequency • Assuming the two variables are independent, you can use the contingency table to find the expected frequency for each cell. • The expected frequency for a cell Er, c in a contingency table is . Copyright © 2015, 2012, and 2009 Pearson Education, Inc. 7

Example: Finding Expected Frequencies Find the expected frequency for each cell in the contingency table. Assume that the variables, favorite way to eat ice cream and gender, are independent. Favorite way to eat ice cream Gender Male Female Total Cup Cone Sundae Sandwich Other Total 600 288 204 24 84 1200 410 1010 340 628 180 384 20 44 50 134 1000 2200 marginal totals Copyright © 2015, 2012, and 2009 Pearson Education, Inc. 8

Solution: Finding Expected Frequencies Favorite way to eat ice cream Gender Male Female Total . Cup Cone Sundae Sandwich Other Total 600 288 204 24 84 1200 410 1010 340 628 180 384 20 44 50 134 1000 2200 Copyright © 2015, 2012, and 2009 Pearson Education, Inc. 9

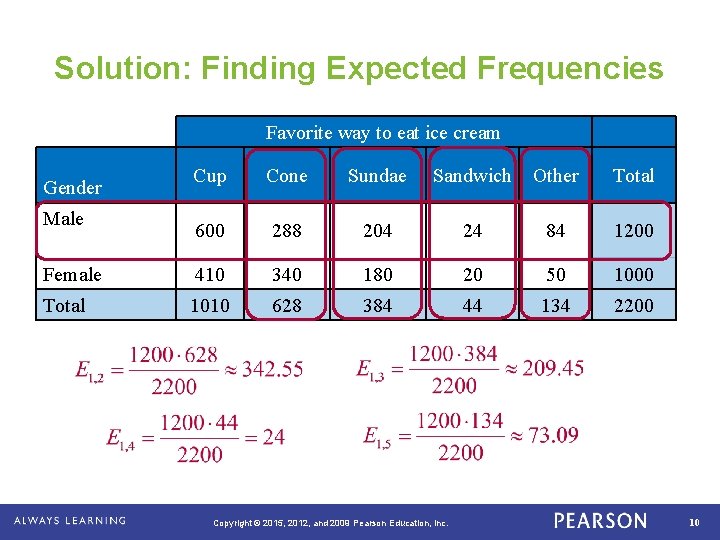
Solution: Finding Expected Frequencies Favorite way to eat ice cream Cup Cone Sundae Sandwich Other Total 600 288 204 24 84 1200 Female 410 340 180 20 50 1000 Total 1010 628 384 44 134 2200 Gender Male . Copyright © 2015, 2012, and 2009 Pearson Education, Inc. 10

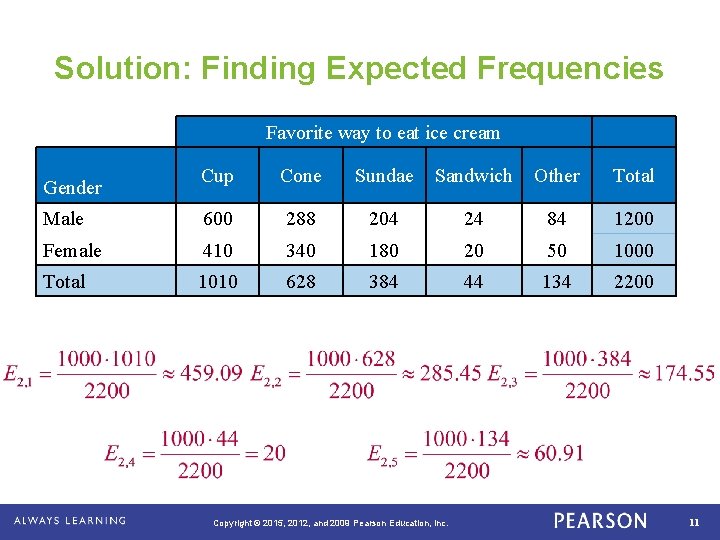
Solution: Finding Expected Frequencies Favorite way to eat ice cream Cup Cone Sundae Sandwich Other Total Male 600 288 204 24 84 1200 Female 410 340 180 20 50 1000 Total 1010 628 384 44 134 2200 Gender . Copyright © 2015, 2012, and 2009 Pearson Education, Inc. 11

Chi-Square Independence Test Chi-square independence test • Used to test the independence of two variables. • Can determine whether the occurrence of one variable affects the probability of the occurrence of the other variable. . Copyright © 2015, 2012, and 2009 Pearson Education, Inc. 12

Chi-Square Independence Test For the chi-square independence test to be used, the following must be true. 1. The observed frequencies must be obtained by using a random sample. 2. Each expected frequency must be greater than or equal to 5. . Copyright © 2015, 2012, and 2009 Pearson Education, Inc. 13

Chi-Square Independence Test • If these conditions are satisfied, then the sampling distribution for the chi-square independence test is approximated by a chi-square distribution with (r – 1)(c – 1) degrees of freedom, where r and c are the number of rows and columns, respectively, of a contingency table. • The test statistic for the chi-square independence test is The test is always a right-tailed test. where O represents the observed frequencies and E represents the expected frequencies. . Copyright © 2015, 2012, and 2009 Pearson Education, Inc. 14

Chi-Square Independence Test In Words In Symbols 1. Verify that the observed frequencies were from a random sample and each expected frequency is at least 5. 2. Identify the claim. State the null and alternative hypotheses. 3. Specify the level of significance. Copyright © 2015, 2012, and 2009 Pearson Education, Inc. State H 0 and Ha. Identify α. 15

Chi-Square Independence Test In Words In Symbols 4. Identify the degrees of freedom. 5. Determine the critical value. 6. Determine the rejection region. d. f. = (r – 1)(c – 1) Use Table 6 in Appendix B. 7. Find the test statistic and sketch the sampling distribution. . Copyright © 2015, 2012, and 2009 Pearson Education, Inc. 16

Chi-Square Independence Test In Words In Symbols 8. Make a decision to reject or fail to reject the null hypothesis. 9. Interpret the decision in the context of the original claim. . Copyright © 2015, 2012, and 2009 Pearson Education, Inc. If χ2 is in the rejection region, reject H 0. Otherwise, fail to reject H 0. 17

Example: Performing a χ2 Independence Test Using the gender/favorite way to eat ice cream contingency table, can you conclude that the adults favorite ways to eat ice cream are related to gender? Use α = 0. 01. Expected frequencies are shown in parentheses. Favorite way to eat ice cream Gender Cone Sundae Sandwich Other Total Male 600 288 204 (550. 91) (342. 55) (209. 45) 24 (24) 84 (73. 09) 1200 Female 410 340 180 (459. 09) (285. 45) (174. 55) 20 (20) 50 (60. 91) 1000 44 134 2200 Total. Cup 1010 628 384 Copyright © 2015, 2012, and 2009 Pearson Education, Inc. 18

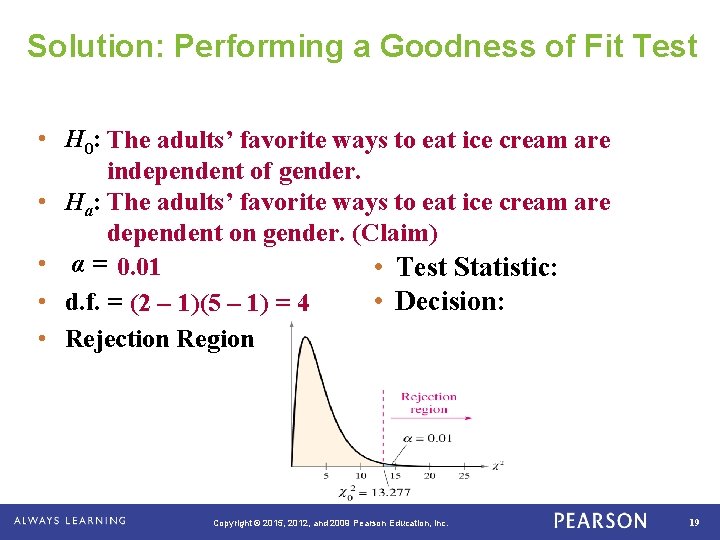
Solution: Performing a Goodness of Fit Test • H 0: The adults’ favorite ways to eat ice cream are independent of gender. • Ha: The adults’ favorite ways to eat ice cream are dependent on gender. (Claim) • α = 0. 01 • Test Statistic: • d. f. = (2 – 1)(5 – 1) = 4 • Decision: • Rejection Region . Copyright © 2015, 2012, and 2009 Pearson Education, Inc. 19

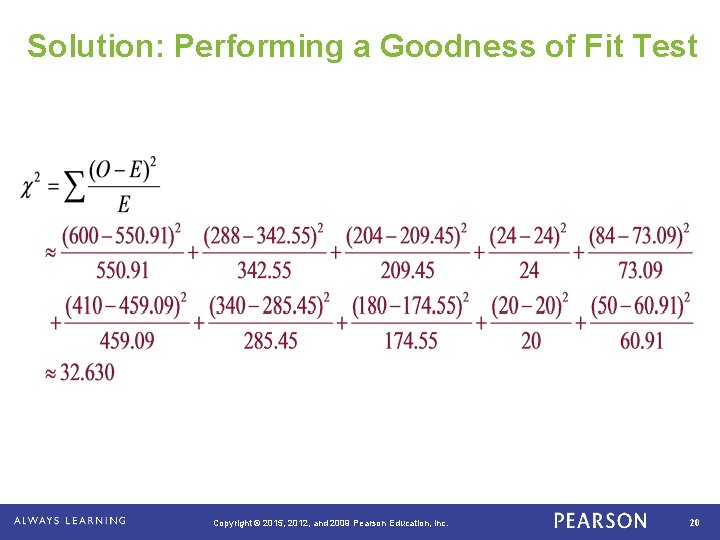
Solution: Performing a Goodness of Fit Test . Copyright © 2015, 2012, and 2009

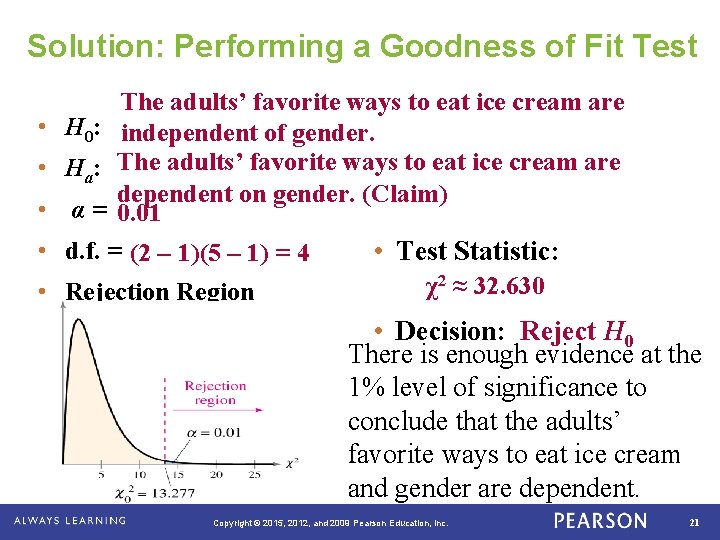
Solution: Performing a Goodness of Fit Test • • • The adults’ favorite ways to eat ice cream are H 0: independent of gender. Ha: The adults’ favorite ways to eat ice cream are dependent on gender. (Claim) α = 0. 01 d. f. = (2 – 1)(5 – 1) = 4 • Test Statistic: 2 ≈ 32. 630 χ Rejection Region • Decision: Reject H 0 There is enough evidence at the 1% level of significance to conclude that the adults’ favorite ways to eat ice cream and gender are dependent. . Copyright © 2015, 2012, and 2009 Pearson Education, Inc. 21

Section 10. 2 Summary • Used a contingency table to find expected frequencies • Used a chi-square distribution to test whether two variables are independent . Copyright © 2015, 2012, and 2009 Pearson Education, Inc. 22