Chapter 10 Chemical Bonding II Chapter 10 Chapter

Chapter 10 Chemical Bonding II Chapter 10

Chapter 10 The Quantum-Mechanical Model of the Atom 10. 1 10. 2 10. 3 10. 4 10. 5 10. 6 10. 7 10. 8 Artificial Sweeteners: Fooled by Molecular Shape VSEPR Theory: The Five Basic Shapes VSEPR Theory: The Effect of Lone Pairs VSEPR Theory: Predicting Molecular Geometries Molecular Shape and Polarity Valence Bond Theory: Orbital Overlap as a Covalent Bond Valence Bond Theory: Hybridization of Atomic Orbitals Molecular Orbital Theory: Electron Delocalization 2

Chapter 9 and 10 Bonding Theories • Lewis Model (Theory) – Ch 9 – Treats electrons as dots and bonds as dashes • Valence Bond theory – Ch 10 – More quantum mechanical view of bonding – Atomic orbitals become hybrid orbitals – Localized on the atom • Molecular Orbital theory – Ch 10 – Fully quantum mechanical view of bonding – Atomic orbitals become molecular orbitals – Delocalized over the entire molecule 3

Chapter 9 and 10 Bonding Theories • Which theory is correct? • Why do we have more than one? • Different theories of bonding are useful to examine different aspect of bonding and chemical behavior. • Valence bond theory and Molecular Orbital theory are more sophisticated and complex 4

Section 10. 1 Artificial Sweeteners: Fooled by Molecular Shape and Artificial Sweeteners • The “taste” of sweetness – Both sucrose (regular table sugar) and artificial sweeteners bind to “receptors” on the tongue that send the sweet signal to the brain. – The shapes have things in common – Receptors are more forgiving when it comes to shape • The calories of sweetness – The enzymes that metabolize sugar and release the energy can’t break down the artificial sweetener. – The shapes are too different – Enzymes are really, really picky about shape 5

Section 10. 1 Artificial Sweeteners: Fooled by Molecular Shape What accounts for Molecular Shape? • VSEPR – Valence Shell Electron Pair Repulsion – Combined with Lewis Model gives a simple model for molecular shape • Valence Bond Theory (10. 6) • Molecular Orbital Theory (10. 8) 6

Section 10. 2 VSEPR Theory: The Five Basic Shapes VSEPR • Electron groups repel each other – An electron group is a single electron, lone pair, single, double or even triple bond • The repulsion between electron groups determines the geometry of the molecule • The preferred geometry has the maximum separation (minimum repulsion) between electron groups. 7

Section 10. 2 VSEPR Theory: The Five Basic Shapes VSEPR – 5 basic shapes • 5 basic molecular shapes for molecules with one central atom depends on • 1. number of electron groups around the central atom • 2. how many of the electron groups are bonding and how many are lone pairs 8

Section 10. 2 VSEPR Theory: The Five Basic Shapes Two Electron Groups: Linear Geometry • Be. Cl 2 180° Linear • Electron Geometry – Two electron groups (single bonds) around Be. To minimize electron repulsions place the groups on opposite sides of the Be atom. – Electron geometry is linear. • Molecular Geometry – Each electron group on beryllium is shared with a chlorine atom (no lone pairs). – The molecular geometry is linear. 9

Section 10. 2 VSEPR Theory: The Five Basic Shapes Two Electron Groups: Linear Geometry • CO 2 180° Linear • Electron Geometry – Two electron groups (double bonds) around C. To minimize electron repulsions place the groups on opposite sides of the C atom. – Electron geometry is linear. • Molecular Geometry – Each electron group on carbon is shared with an oxygen atom (no lone pairs). – The molecular geometry is linear. 10

Section 10. 2 VSEPR Theory: The Five Basic Shapes Three Electron Groups: Trigonal Planar Geometry • CH 2 O ~120° Trigonal Planar • Electron Geometry – Three electron groups (single/double bonds) around C. To minimize electron repulsions place the groups 120 degrees apart (in the plane). – Electron geometry is trigonal planar. • Molecular Geometry – Each electron group on C is shared with an H/O atom (no lone pairs). – The molecular geometry is trigonal planar. 11

Section 10. 2 VSEPR Theory: The Five Basic Shapes Four Electron Groups: Tetrahedral Geometry • CH 4 109. 5° Tetrahedral • Electron Geometry – Four electron groups (single bonds) around C. To minimize electron repulsions place the groups 109. 5 degrees apart (out of the plane). Electron geometry is tetrahedral. • Molecular Geometry – Each electron group on C is shared with an H atom (no lone pairs). – The molecular geometry is also tetrahedral 12

Section 10. 2 VSEPR Theory: The Five Basic Shapes Electron Geometry with Balloons 13

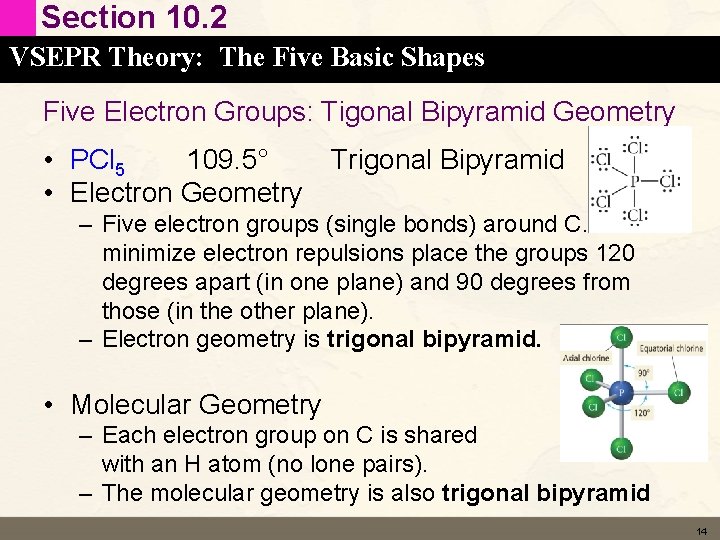
Section 10. 2 VSEPR Theory: The Five Basic Shapes Five Electron Groups: Tigonal Bipyramid Geometry • PCl 5 109. 5° Trigonal Bipyramid • Electron Geometry – Five electron groups (single bonds) around C. To minimize electron repulsions place the groups 120 degrees apart (in one plane) and 90 degrees from those (in the other plane). – Electron geometry is trigonal bipyramid. • Molecular Geometry – Each electron group on C is shared with an H atom (no lone pairs). – The molecular geometry is also trigonal bipyramid 14

Section 10. 2 VSEPR Theory: The Five Basic Shapes Six Electron Groups: Octahedral Geometry • SF 6 90° Octahedral • Electron Geometry – Six electron groups (single bonds) around C. To minimize electron repulsions place the groups 90 degrees apart (in one plane) and 90 degrees from those (in the other plane). – Electron geometry is octahedral. • Molecular Geometry – Each electron group on C is shared with an H atom (no lone pairs). – The molecular geometry is also octahedral 15

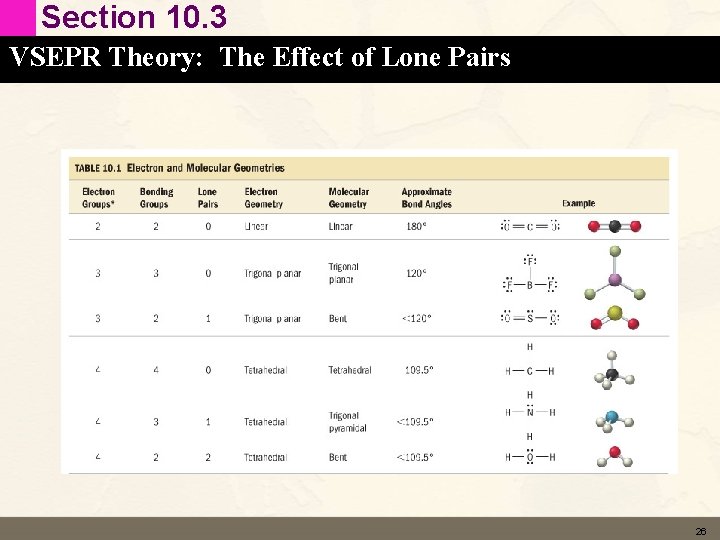
Section 10. 3 VSEPR Theory: The Effect of Lone Pairs and Molecular Geometry • In all of the previous examples – – Bonded atom for every electron group Electron Geometry = Molecular Geometry Not always the case Lone pairs cause there to be a difference between the electron geometry and the molecular geometry – Maintain a gradient of these ions in nerve cells 16

Section 10. 3 VSEPR Theory: The Effect of Lone Pairs Three Electron Groups with Lone Pairs • SO 2 < 120° Trigonal Planar • Electron Geometry – Three electron groups (single/double bonds and a lone pair) around S. – Electron geometry is trigonal planar. • Molecular Geometry – Now we have a lone pair. – The molecular geometry is not trigonal planar but bent. 17

Section 10. 3 VSEPR Theory: The Effect of Lone Pairs Four Electron Groups with Lone Pairs • NH 3 107° Trigonal Pyramidal • Electron Geometry – Four electron groups (single bonds and a sinlge lone pair) around N. – Electron geometry is tetrahedral. • Molecular Geometry – Now we have a lone pair. – The molecular geometry is not tetrahedral but trigonal pyramidal. 18

Section 10. 3 VSEPR Theory: The Effect of Lone Pairs Four Electron Groups with Lone Pairs • H 2 O 104. 5° Bent • Electron Geometry – Four electron groups (single bonds and a 2 lone pairs) around O. – Electron geometry is tetrahedral. • Molecular Geometry – Now we have 2 lone pairs. – The molecular geometry is not tetrahedral but Bent. 19

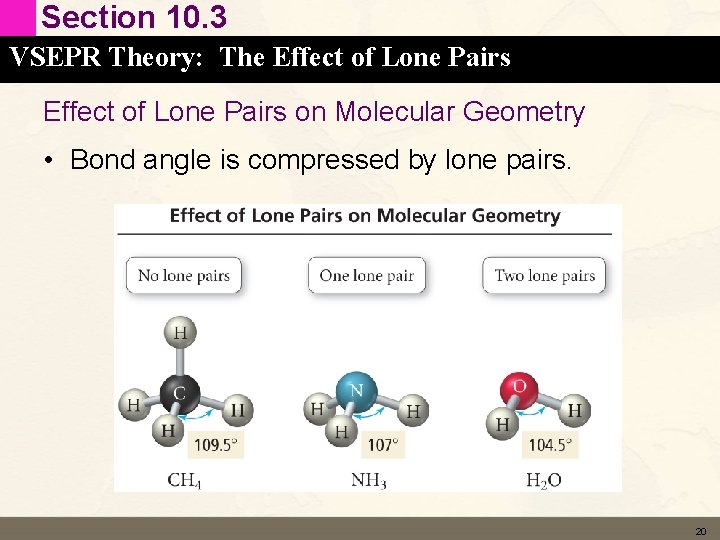
Section 10. 3 VSEPR Theory: The Effect of Lone Pairs on Molecular Geometry • Bond angle is compressed by lone pairs. 20

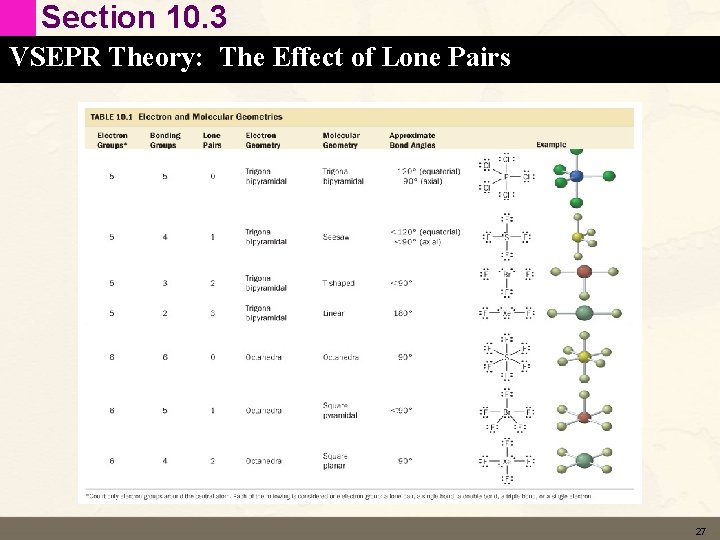
Section 10. 3 VSEPR Theory: The Effect of Lone Pairs Five Electron Groups with Lone Pairs • SF 4 104. 5° seesaw • Electron Geometry – Five electron groups (single bonds and a lone pair) around S. – Electron geometry is trigonal bipyramid. • Molecular Geometry – Now we have a lone pair. – The molecular geometry is not tetrahedral but seesaw. 21

Section 10. 3 VSEPR Theory: The Effect of Lone Pairs Learning Check • Why is the lone pair on SF 4 in the equitorial plane instead of the axial plane? 22

Section 10. 3 VSEPR Theory: The Effect of Lone Pairs Five Electron Groups with Lone Pairs • Br. F 3 90° T-shaped • Electron Geometry – Five electron groups (single bonds and 2 lone pairs) around Br. – Electron geometry is trigonal bipyramid. • Molecular Geometry – Now we have 2 lone pairs. – The molecular geometry is not tetrahedral but T-shaped. 23

Section 10. 3 VSEPR Theory: The Effect of Lone Pairs Six Electron Groups with Lone Pairs • Br. F 5 90° Square Pyramidal • Electron Geometry – Sixelectron groups (single bonds and a lone pairs) around Br. – Electron geometry is octahedral. • Molecular Geometry – Now we have a lone pair. – The molecular geometry is not octahedral but square pyramidal. 24

Section 10. 3 VSEPR Theory: The Effect of Lone Pairs Six Electron Groups with Lone Pairs • Xe. F 4 90° Square Planar • Electron Geometry – Six electron groups (single bonds and 2 lone pairs) around Xe. – Electron geometry is octahedral. • Molecular Geometry – Now we have 2 lone pairs. – The molecular geometry is not octahedral but square planar. 25

Section 10. 3 VSEPR Theory: The Effect of Lone Pairs 26

Section 10. 3 VSEPR Theory: The Effect of Lone Pairs 27

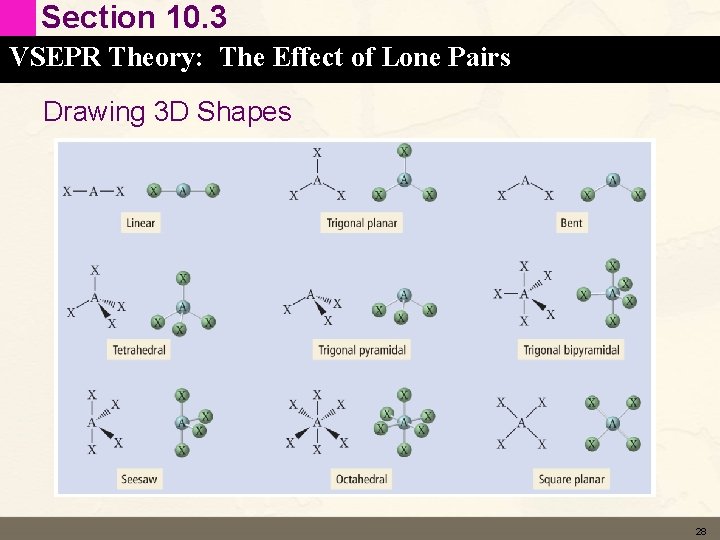
Section 10. 3 VSEPR Theory: The Effect of Lone Pairs Drawing 3 D Shapes 28

Section 10. 4 VSEPR Theory: Predicting Molecular Geometries How to predict Molecular Geometry • Lewis Structure • Count number of electron groups around central atom – Basic shape • Compare # bonding groups to # lone pairs – Modifies basic shape 29

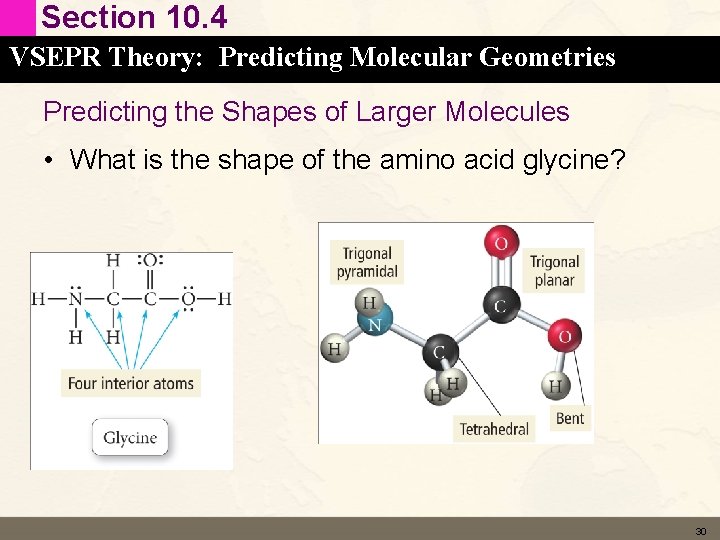
Section 10. 4 VSEPR Theory: Predicting Molecular Geometries Predicting the Shapes of Larger Molecules • What is the shape of the amino acid glycine? 30

Section 10. 5 Molecular Shape and Polarity Polar bonds do not necessarily mean polar molecules • Symmetry cancels polarity • A symmetrical molecule with polar bonds will be non polar – Polarities cancel • An asymmetrical molecule with polar bonds with be polar – Polarities sum 31

Section 10. 5 Molecular Shape and Polarity Polar bonds do not necessarily mean polar molecules • HCl is not symmetrical – polar molecule • CO 2 is symmetrical - Symmetry cancels polarity 32

Section 10. 5 Molecular Shape and Polarity Polar bonds do not necessarily mean polar molecules • H 2 O is not symmetrical. 33

Section 10. 5 Molecular Shape and Polarity Predicting Molecular Shape and Polarity • Draw Lewis Structure and determine Molecular Geometry • Determine if the molecule contains polar bonds. • Determine if the polar bonds add together to form a net dipole moment. 34

Section 10. 5 Molecular Shape and Polarity Polar bonds do not necessarily mean polar molecules • Go to the Molecular Modeling Lab and predict the polarity of the molecules based on your drawings. 35

Section 10. 6 Valence Bond Theory: Orbital Overlap as a Covalent Bond Valence Bond Theory • Lewis Model uses dots to represent electrons • Valence bond theory treats electrons in a more quantum mechanical manner – We do a fairly qualitative analysis – The quantitative approach to bonding predicts many properties of molecules • • Bond length Bond strength Molecular geometry Dipole moments 36

Section 10. 6 Valence Bond Theory: Orbital Overlap as a Covalent Bond Valence Bond Theory • Electrons reside in quantum mechanical orbitals – Standard s, p, d, f orbitals – Hybridized atomic orbitals (Section 10. 7) 37

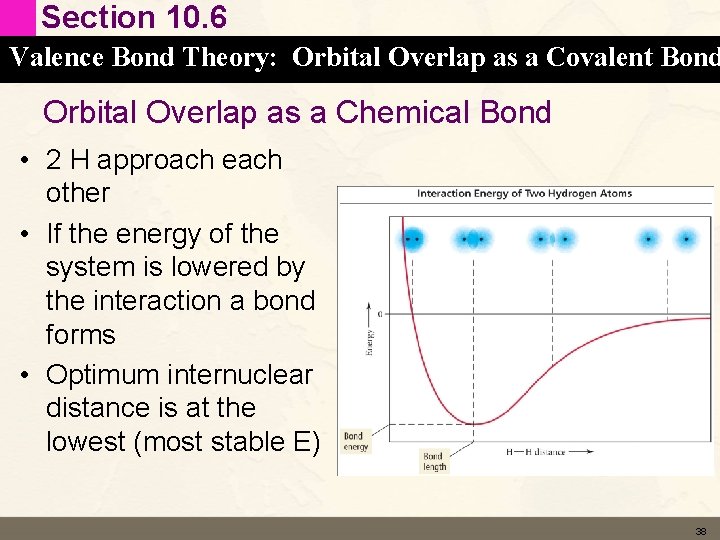
Section 10. 6 Valence Bond Theory: Orbital Overlap as a Covalent Bond Orbital Overlap as a Chemical Bond • 2 H approach each other • If the energy of the system is lowered by the interaction a bond forms • Optimum internuclear distance is at the lowest (most stable E) 38

Section 10. 6 Valence Bond Theory: Orbital Overlap as a Covalent Bond Orbital Overlap as a Chemical Bond • Bond formation • The interaction of two atoms is usually negative (stabilizing) when the interacting atomic orbitals contain a total of two electrons that can spin pair (orient with opposing spins). • Two atomic orbitals overlap and electrons occupying them align with opposite spins. • H 1 s +H 1 s = H 2 1 s 39

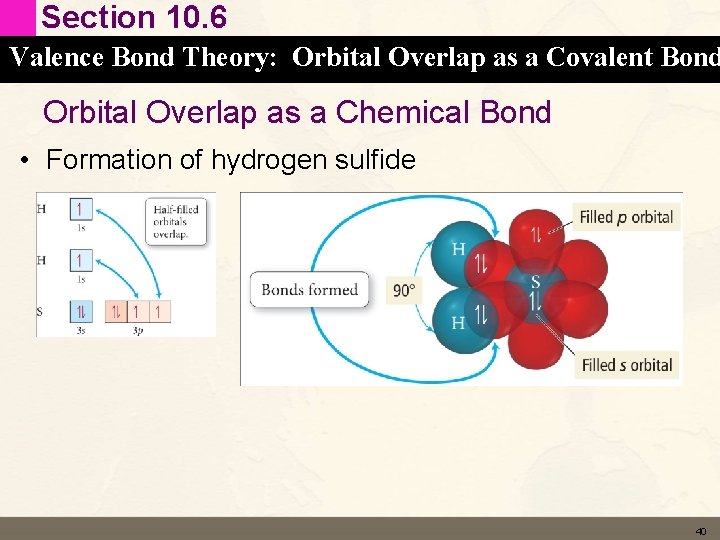
Section 10. 6 Valence Bond Theory: Orbital Overlap as a Covalent Bond Orbital Overlap as a Chemical Bond • Formation of hydrogen sulfide 40

Section 10. 6 Valence Bond Theory: Orbital Overlap as a Covalent Bond Learning Check • The experimentally determined bond angle for H 2 S is 92. What is the value predicted by the Lewis Model? What is the value predicted by valence bond theory? Whys do you think one model gives a more accurate value than the other? 41

Section 10. 6 Valence Bond Theory: Orbital Overlap as a Covalent Bond Orbital Overlap as a Chemical Bond • Summary of valence bond theory • 1. The valence electrons of atoms reside in QM atomic orbitals (s, p, d, or f) or hybrid orbitals. • 2. Chemical bond results from overlap of half filled orbitals or a filled and empty orbital (coordinate covalent bond) • 3. Geometry of the overlapping orbitals determines the shape of the molecule. 42

Section 10. 7 Valence Bond Theory: Hybridization of Atomic Orbitals Hybridized orbitals • Overlap of half filled orbitals explains the formation of H 2 S but this approach does not work for everything. • How do we explain the formation of CH 4 from C and H. • Valence bond theory would only predict CH 2. • Yet CH 4 (methane) exists 43

Section 10. 7 Valence Bond Theory: Hybridization of Atomic Orbitals Hybridized orbitals • Maybe orbitals in molecules are different from orbitals in atoms • Hybridization – standard atomic orbitals are combined to form new atomic orbitals called hybrid orbitals • Still localized on a particular atom • Tend to form on atoms that make multiple bonds (central atoms) 44

Section 10. 7 Valence Bond Theory: Hybridization of Atomic Orbitals Hybridized orbitals • 1. Number of standard orbitals in = number of hybrid orbitals out • 2. Particular combinations of standard orbitals determines shapes and energies of hybrid orbitals • 3. The type of hybridization that occurs is the one with the lowest overall energy for the molecule. 45

Section 10. 7 Valence Bond Theory: Hybridization of Atomic Orbitals sp 3 hybridization • We can account for the formation of CH 4 by the hybridization of the one 2 s and three 2 p orbitals of carbon into four sp 3 hybrid orbitals 46

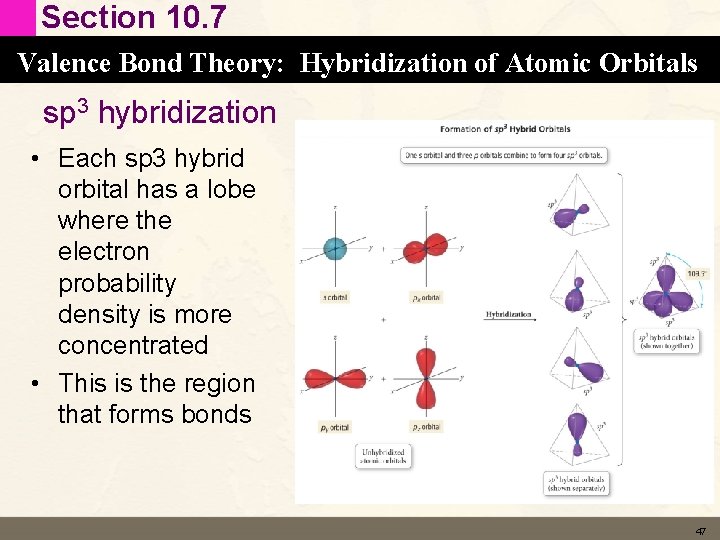
Section 10. 7 Valence Bond Theory: Hybridization of Atomic Orbitals sp 3 hybridization • Each sp 3 hybrid orbital has a lobe where the electron probability density is more concentrated • This is the region that forms bonds 47

Section 10. 7 Valence Bond Theory: Hybridization of Atomic Orbitals sp 3 hybridization • Carbons 4 valence electrons occupy the orbitals singly with parrallell spins (Hunds Rule) • Thus, C has four half-filled orbitals which can form 4 bonds with hydrogen atoms 48

Section 10. 7 Valence Bond Theory: Hybridization of Atomic Orbitals sp 3 hybridization • Geometry predicted by Valence bond theory is tetrahedral with bond angles on 109. 5 degrees • Agrees well with experimental values and prediction of Lewis Model 49

Section 10. 7 Valence Bond Theory: Hybridization of Atomic Orbitals Learning Check • Ammonia (NH 3) has tetrahedral molecular geometry. Explain how this is possible using hybrid orbital theory. 50

Section 10. 7 Valence Bond Theory: Hybridization of Atomic Orbitals sp 2 hybridization and double bonds • Hybridization of one s and two p orbitals results in three sp 2 hybrids and one leftover unhybridized p orbital. 51

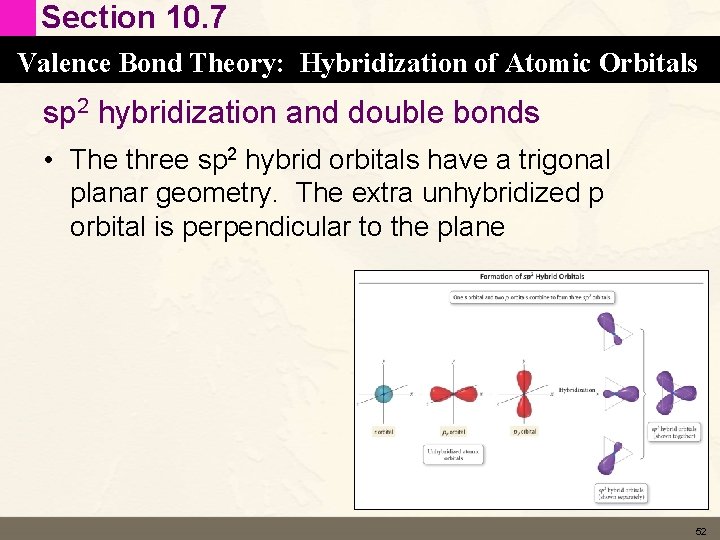
Section 10. 7 Valence Bond Theory: Hybridization of Atomic Orbitals sp 2 hybridization and double bonds • The three sp 2 hybrid orbitals have a trigonal planar geometry. The extra unhybridized p orbital is perpendicular to the plane 52

Section 10. 7 Valence Bond Theory: Hybridization of Atomic Orbitals sp 2 hybridization and double bonds • An example of sp 2 hybridization is formaldehyde, H 2 CO. • The unhybridized valence electron configurations of the atoms look like this. • Since C is the central atom and needs to make three bonds we will start out with sp 2 hybridization. 53

Section 10. 7 Valence Bond Theory: Hybridization of Atomic Orbitals sp 2 hybridization and double bonds • An example of sp 2 hybridization is formaldehyde, H 2 CO. • The unhybridized valence electron configurations of the atoms look like this. • Since C is the central atom and needs to make three bonds we will start out with sp 2 hybridization. 54

Section 10. 7 Valence Bond Theory: Hybridization of Atomic Orbitals sp 2 hybridization and double bonds • Each sp 2 is half filled and can bond with the two H and the oxygen. • The unhybridized p orbital is also half filled and can be used to form a bond – this is actually the second part of the double bond between carbon and oxygen. 55

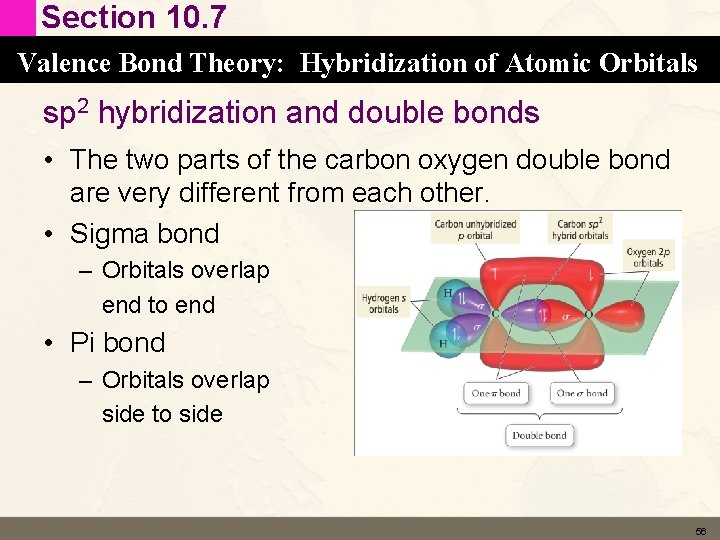
Section 10. 7 Valence Bond Theory: Hybridization of Atomic Orbitals sp 2 hybridization and double bonds • The two parts of the carbon oxygen double bond are very different from each other. • Sigma bond – Orbitals overlap end to end • Pi bond – Orbitals overlap side to side 56

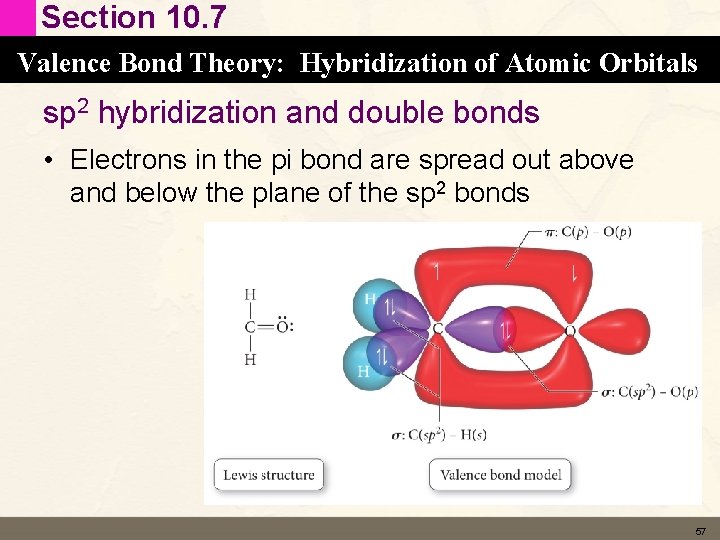
Section 10. 7 Valence Bond Theory: Hybridization of Atomic Orbitals sp 2 hybridization and double bonds • Electrons in the pi bond are spread out above and below the plane of the sp 2 bonds 57

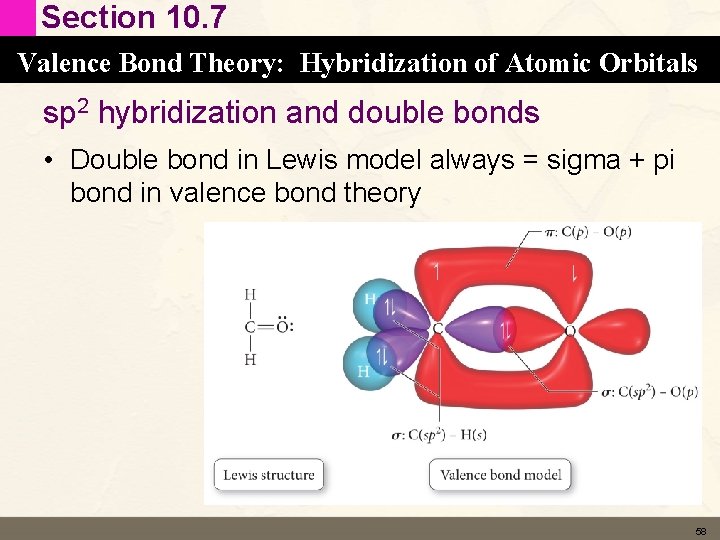
Section 10. 7 Valence Bond Theory: Hybridization of Atomic Orbitals sp 2 hybridization and double bonds • Double bond in Lewis model always = sigma + pi bond in valence bond theory 58

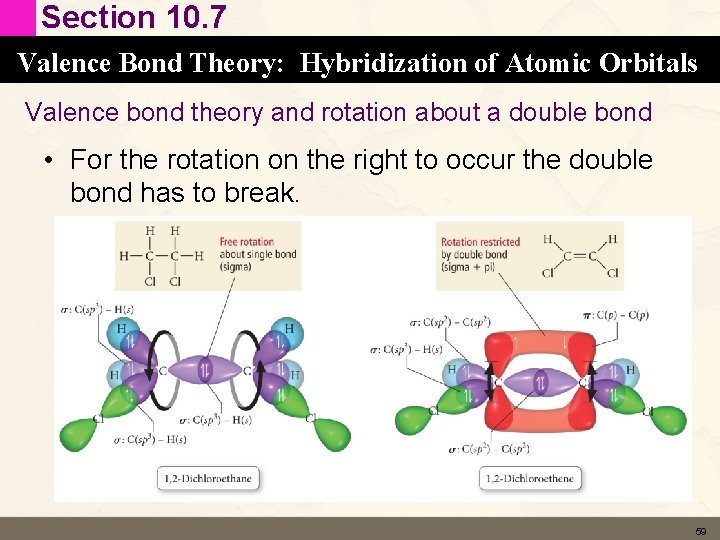
Section 10. 7 Valence Bond Theory: Hybridization of Atomic Orbitals Valence bond theory and rotation about a double bond • For the rotation on the right to occur the double bond has to break. 59

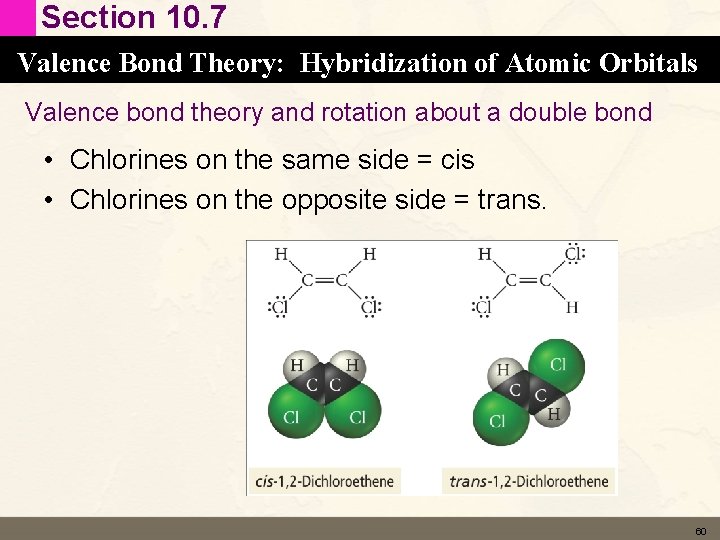
Section 10. 7 Valence Bond Theory: Hybridization of Atomic Orbitals Valence bond theory and rotation about a double bond • Chlorines on the same side = cis • Chlorines on the opposite side = trans. 60

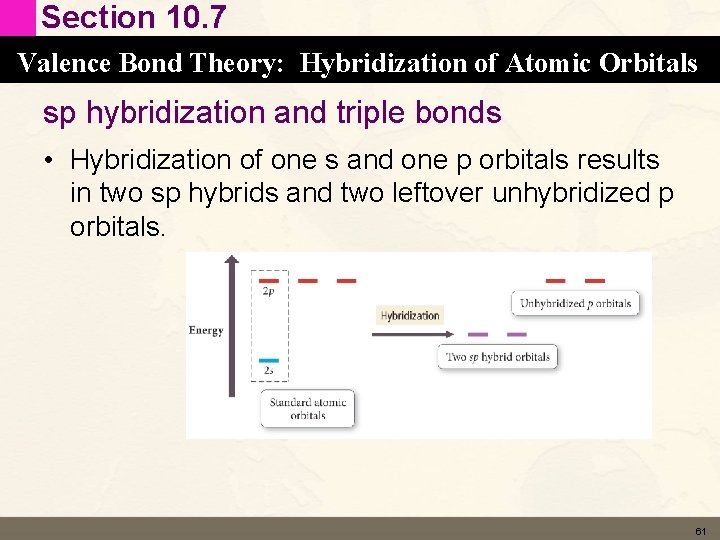
Section 10. 7 Valence Bond Theory: Hybridization of Atomic Orbitals sp hybridization and triple bonds • Hybridization of one s and one p orbitals results in two sp hybrids and two leftover unhybridized p orbitals. 61

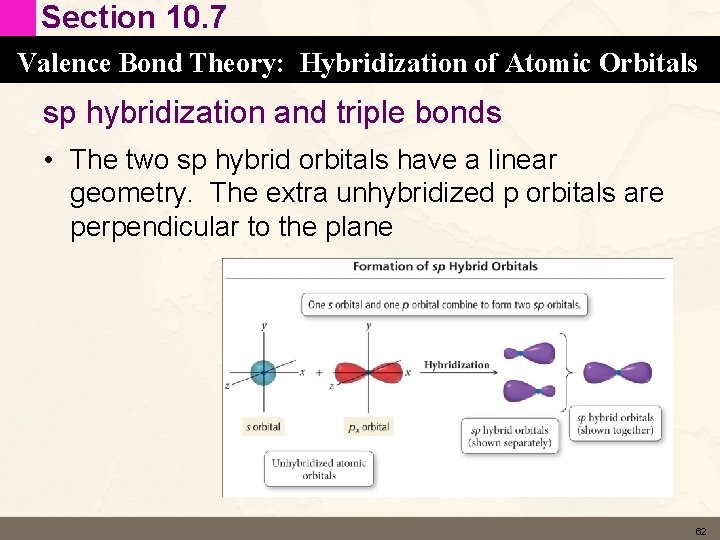
Section 10. 7 Valence Bond Theory: Hybridization of Atomic Orbitals sp hybridization and triple bonds • The two sp hybrid orbitals have a linear geometry. The extra unhybridized p orbitals are perpendicular to the plane 62

Section 10. 7 Valence Bond Theory: Hybridization of Atomic Orbitals sp hybridization and triple bonds • An example of sp hybridization is acetylene C 2 H 2. • The unhybridized valence electron configurations of the atoms look like this. • Since C is the central atom and needs to make two sigma bonds we will start out with sp hybridization. 63

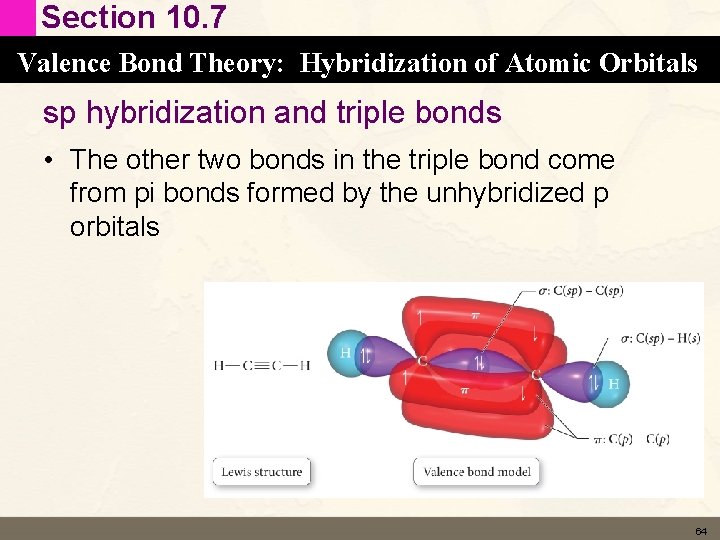
Section 10. 7 Valence Bond Theory: Hybridization of Atomic Orbitals sp hybridization and triple bonds • The other two bonds in the triple bond come from pi bonds formed by the unhybridized p orbitals 64

Section 10. 7 Valence Bond Theory: Hybridization of Atomic Orbitals sp 3 d and sp 3 d 2 hybridization • According to the Lewis Model elements in period 3 and below can form expanded octets (more than 8 valence electrons). • Equivalent concept in valence bond theory is hybridization involving d orbitals. 65

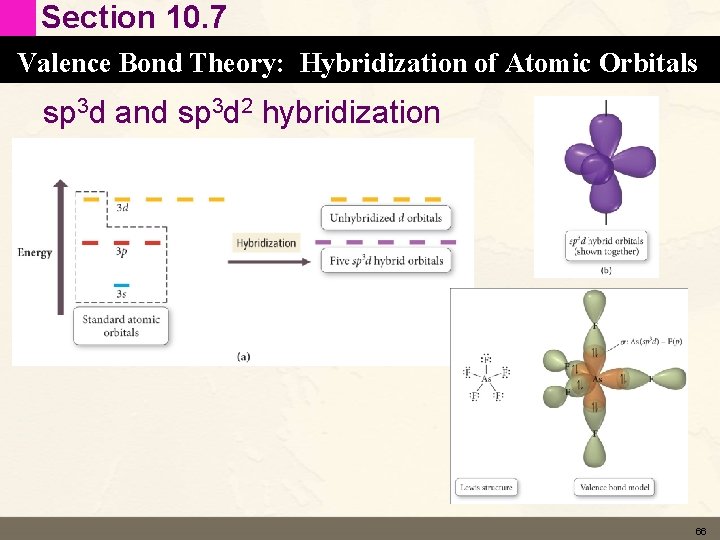
Section 10. 7 Valence Bond Theory: Hybridization of Atomic Orbitals sp 3 d and sp 3 d 2 hybridization 66

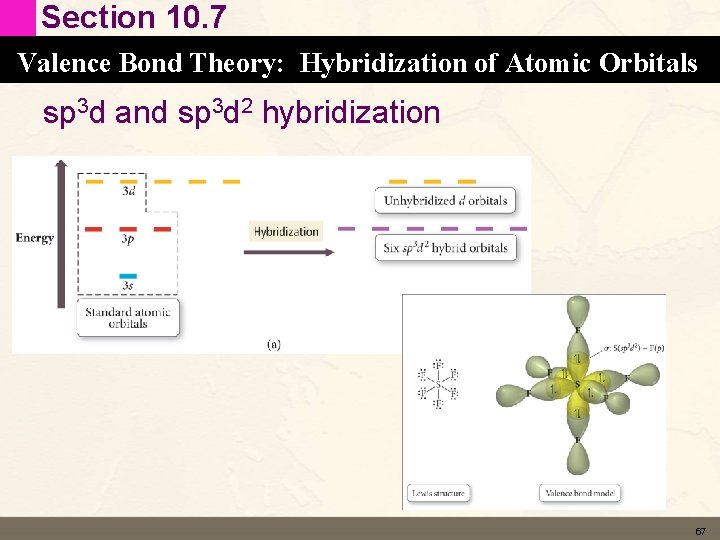
Section 10. 7 Valence Bond Theory: Hybridization of Atomic Orbitals sp 3 d and sp 3 d 2 hybridization 67

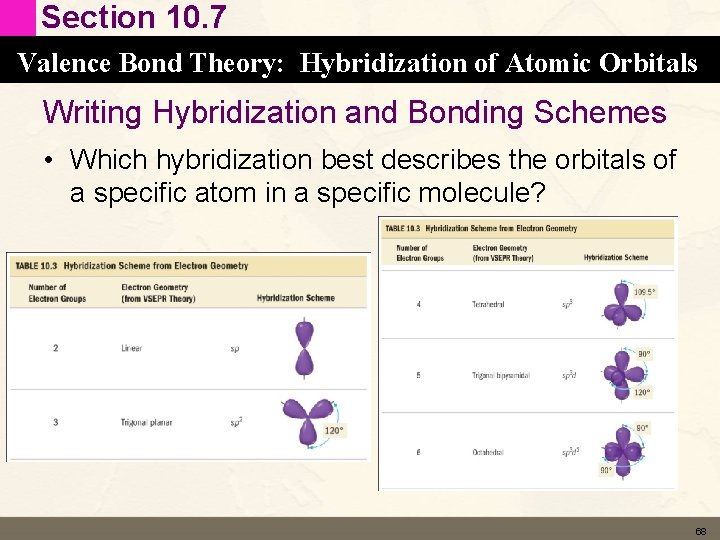
Section 10. 7 Valence Bond Theory: Hybridization of Atomic Orbitals Writing Hybridization and Bonding Schemes • Which hybridization best describes the orbitals of a specific atom in a specific molecule? 68

Section 10. 7 Valence Bond Theory: Hybridization of Atomic Orbitals Learning Check • Assign a hybridization to each atom in the Molecular Geometry Lab 69

Section 10. 8 Molecular Orbital Theory: Electron Delocalization Valence Bond vs Molecular Orbital Theory • Valence bond theory vs VSEPR – Electrons are dots and bonds are dashes – Valence bond theory – atomic orbitals mix to form hybrid orbitals – still localized on an atom • Valence bond theory explains things that VSEPR can’t such as rigidity of double bond • Still has some limitations • Assumes that electrons reside in QM orbitals calculated for atoms – What if we could calculate QM orbitals for entire molecule instead. 70

Section 10. 8 Molecular Orbital Theory: Electron Delocalization Molecular Orbital Theory • Do we actually solve the Schrodinger Equation for a Molecule? – – No way? Way to complicated We plug in what is called a “trial function” We solve the equation using the trial function and determine the energy of resulting molecular orbital – Lowest energy wins. 71

Section 10. 8 Molecular Orbital Theory: Electron Delocalization Linear Combination of Atomic Orbitals (LCAO) • The “trial function” that gives the lowest energy • Linear combination of Atomic Orbitals – Weighted linear sum (linear average) of valence atomic orbitals • Sounds just like valence bond theory but the critical difference is that while both are weighted linear sums – hybrid orbitals are localized on an atom and molecular orbitals are delocalized over the entire molecule 72

Section 10. 8 Molecular Orbital Theory: Electron Delocalization Linear Combination of Atomic Orbitals (LCAO) • Remember that electrons behave as waves so that when they overlap the pattern can be constructive or destructive. 73

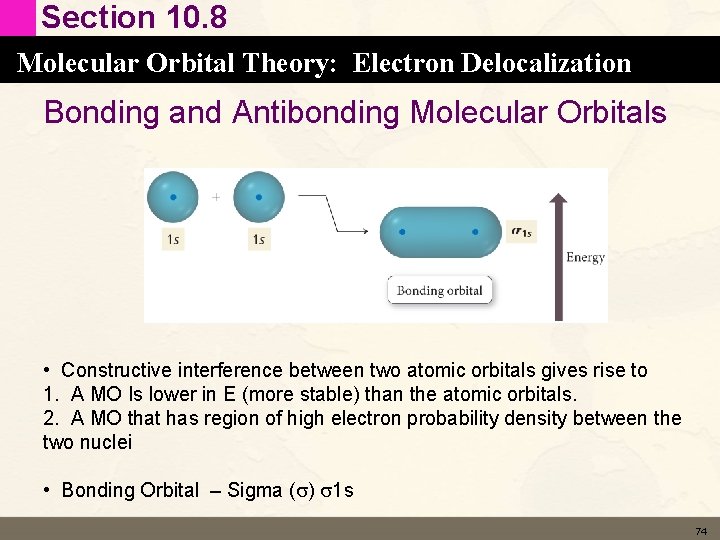
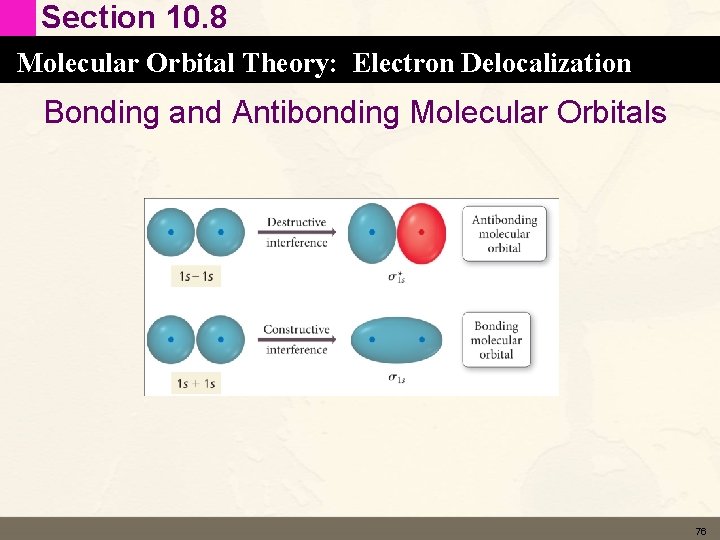
Section 10. 8 Molecular Orbital Theory: Electron Delocalization Bonding and Antibonding Molecular Orbitals • Constructive interference between two atomic orbitals gives rise to 1. A MO Is lower in E (more stable) than the atomic orbitals. 2. A MO that has region of high electron probability density between the two nuclei • Bonding Orbital – Sigma (s) s 1 s 74

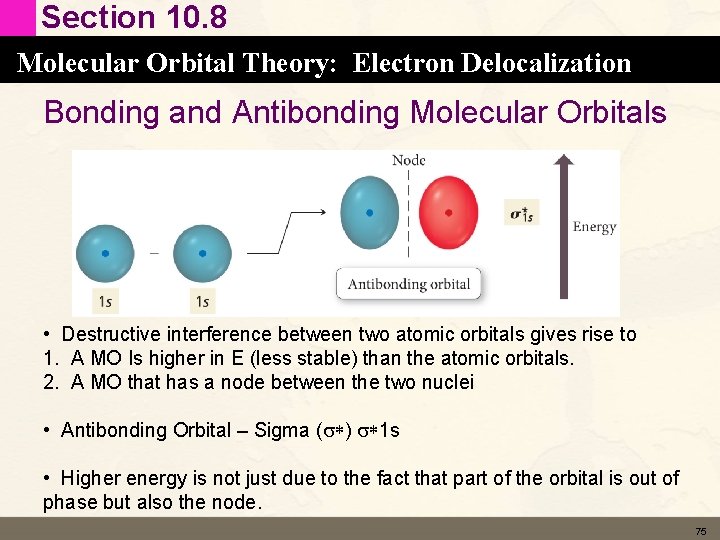
Section 10. 8 Molecular Orbital Theory: Electron Delocalization Bonding and Antibonding Molecular Orbitals • Destructive interference between two atomic orbitals gives rise to 1. A MO Is higher in E (less stable) than the atomic orbitals. 2. A MO that has a node between the two nuclei • Antibonding Orbital – Sigma (s*) s*1 s • Higher energy is not just due to the fact that part of the orbital is out of phase but also the node. 75

Section 10. 8 Molecular Orbital Theory: Electron Delocalization Bonding and Antibonding Molecular Orbitals 76

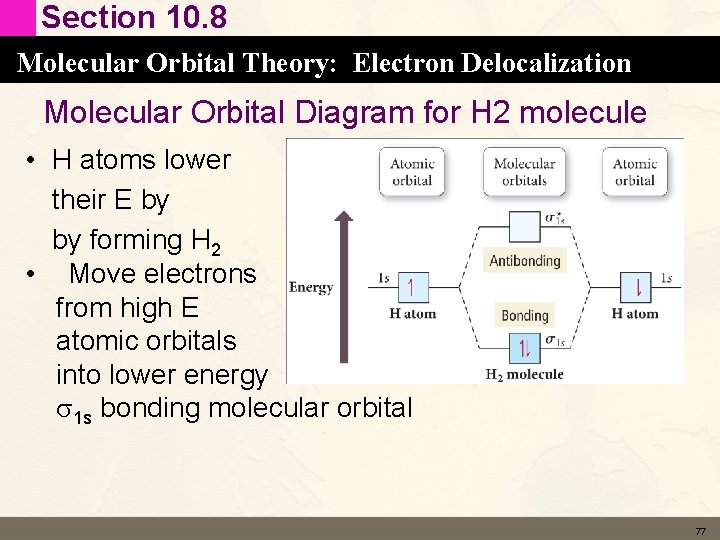
Section 10. 8 Molecular Orbital Theory: Electron Delocalization Molecular Orbital Diagram for H 2 molecule • H atoms lower their E by by forming H 2 • Move electrons from high E atomic orbitals into lower energy s 1 s bonding molecular orbital 77

Section 10. 8 Molecular Orbital Theory: Electron Delocalization Bond order 2 electrons in bonding MO and none in anitbonding • Bond order = 1 78

Section 10. 8 Molecular Orbital Theory: Electron Delocalization Bond order • Bond order predicts whether or not a molecule will be stable • Positive bond order means there are more electrons in bonding MO than in antibonding MO – Electrons have lower energy than they did in isolated atoms – A chemical bond will form • Higher the bond order the stronger the bond • Negative (or 0 bond order) indicates a bond will not form 79

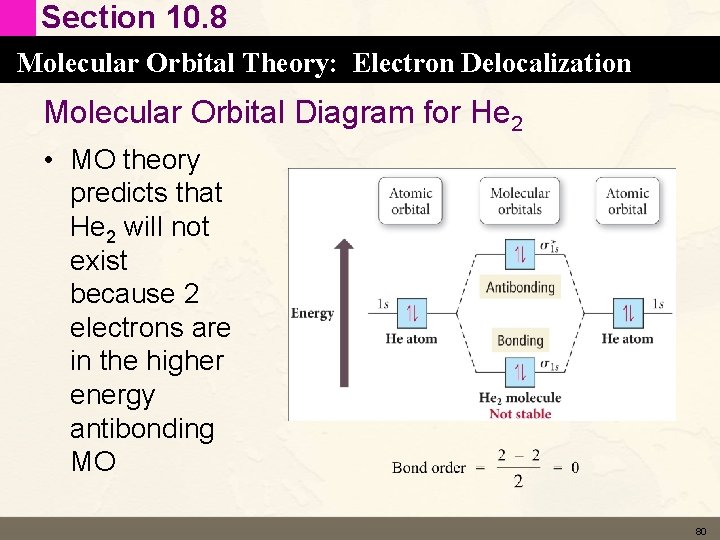
Section 10. 8 Molecular Orbital Theory: Electron Delocalization Molecular Orbital Diagram for He 2 • MO theory predicts that He 2 will not exist because 2 electrons are in the higher energy antibonding MO 80

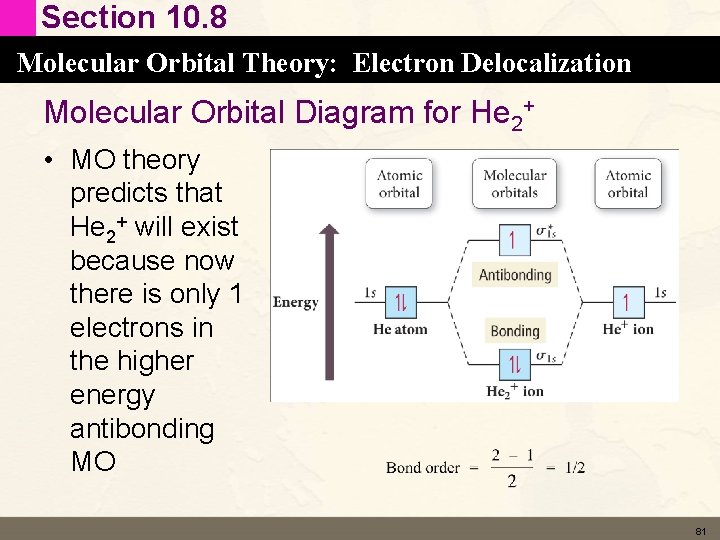
Section 10. 8 Molecular Orbital Theory: Electron Delocalization Molecular Orbital Diagram for He 2+ • MO theory predicts that He 2+ will exist because now there is only 1 electrons in the higher energy antibonding MO 81

Section 10. 8 Molecular Orbital Theory: Electron Delocalization Learning Check • Use MO theory to predict the bond order in H 2– and H 2+. Indicate if the H 2– and H 2+ are stronger or weaker bonds than H 2. 82

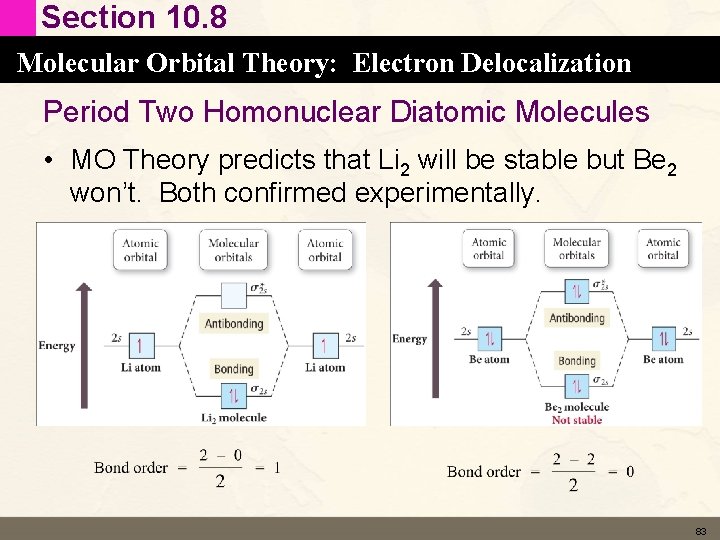
Section 10. 8 Molecular Orbital Theory: Electron Delocalization Period Two Homonuclear Diatomic Molecules • MO Theory predicts that Li 2 will be stable but Be 2 won’t. Both confirmed experimentally. 83

Section 10. 8 Molecular Orbital Theory: Electron Delocalization Period Two Homonuclear Diatomic Molecules • Once we get past Be we start filling p orbitals. • The shape of the MO formed from the combination of 2 s orbitals was fairly straightforward. • The shapes of the MO from the p orbitals can be a little harder to visualize • Essentially the same idea as hybrid orbital theory – End to end overlap for a single (sigma/s) bond – Side to side overlap for a double or triple (pi/p) bond 84

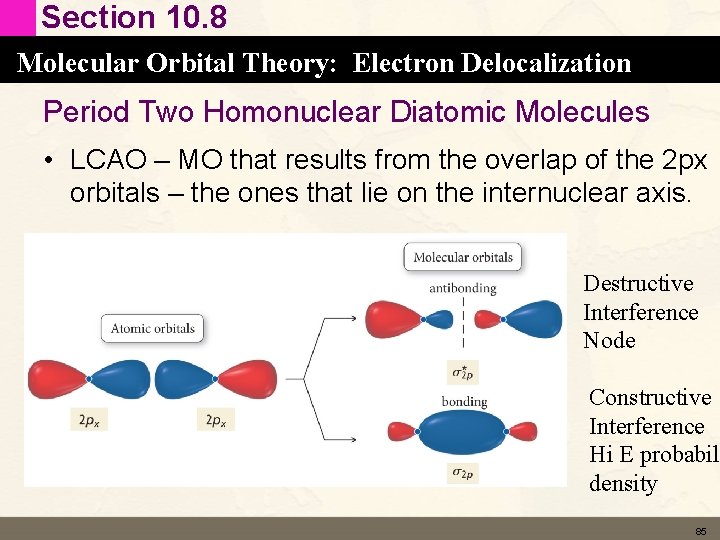
Section 10. 8 Molecular Orbital Theory: Electron Delocalization Period Two Homonuclear Diatomic Molecules • LCAO – MO that results from the overlap of the 2 px orbitals – the ones that lie on the internuclear axis. Destructive Interference Node Constructive Interference Hi E probabili density 85

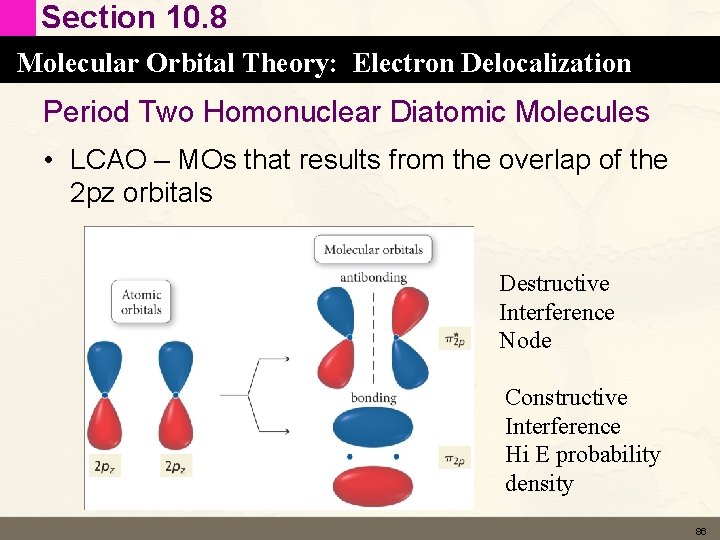
Section 10. 8 Molecular Orbital Theory: Electron Delocalization Period Two Homonuclear Diatomic Molecules • LCAO – MOs that results from the overlap of the 2 pz orbitals Destructive Interference Node Constructive Interference Hi E probability density 86

Section 10. 8 Molecular Orbital Theory: Electron Delocalization Period Two Homonuclear Diatomic Molecules • Remember the region of high electron probability density in the p 2 p (blue) is actually spread out above and below the plane of the s 2 p– just like the p bond in valence bond theory. 87

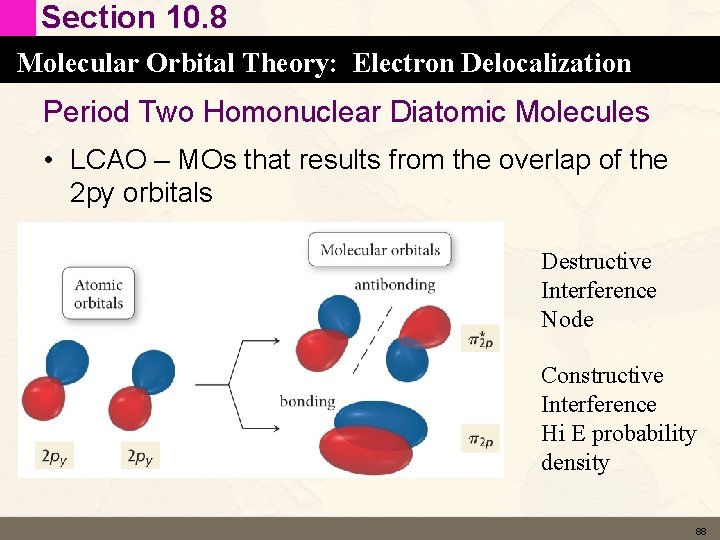
Section 10. 8 Molecular Orbital Theory: Electron Delocalization Period Two Homonuclear Diatomic Molecules • LCAO – MOs that results from the overlap of the 2 py orbitals Destructive Interference Node Constructive Interference Hi E probability density 88

Section 10. 8 Molecular Orbital Theory: Electron Delocalization Period Two Homonuclear Diatomic Molecules • Now the region of high electron probability density in the p 2 p (blue) is actually spread out in fron of and behind the plane of the s 2 p– just like the second p bond in valence bond theory. 89

Section 10. 8 Molecular Orbital Theory: Electron Delocalization MO diagrams for B 2 through Ne 2 • Once we introduce p bonds the MO diagrams get a little more complex • To make things worse the order of the energy for the MO diagram for B 2, C 2 and N 2 are different than the order for O 2, F 2 and Ne 2 90

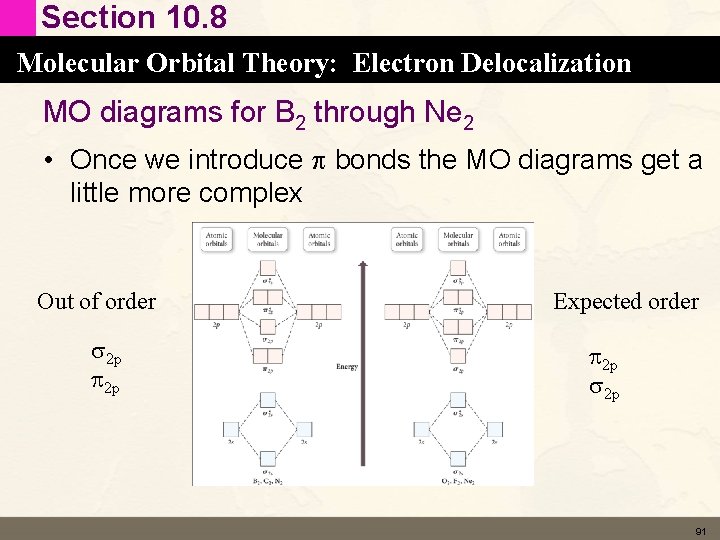
Section 10. 8 Molecular Orbital Theory: Electron Delocalization MO diagrams for B 2 through Ne 2 • Once we introduce p bonds the MO diagrams get a little more complex Out of order s 2 p p 2 p Expected order p 2 p s 2 p 91

Section 10. 8 Molecular Orbital Theory: Electron Delocalization MO diagrams for B 2 through Ne 2 • Valence bond theory – atomic orbitals mix to form hybrid orbitals – still localized on an atom • MO theory – atomic orbitals mix to form molecular orbitals than are delocalized over the entire molecule • In reality in MO theory there is a bit of mixing of the atomic orbitals that make up the molecular orbitals. • That’s why the MO that result can have E that are different from what we predict. 92

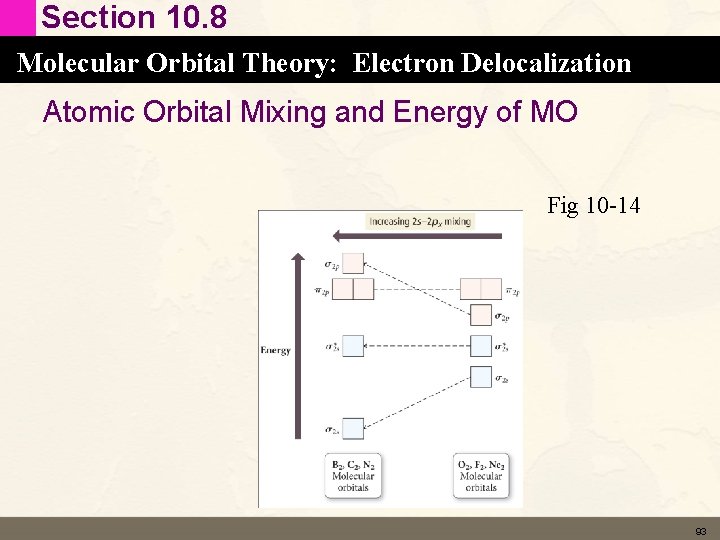
Section 10. 8 Molecular Orbital Theory: Electron Delocalization Atomic Orbital Mixing and Energy of MO Fig 10 -14 93

Section 10. 8 Molecular Orbital Theory: Electron Delocalization Atomic Orbital Mixing and Energy of MO Fig 10 -15 MO diagrams for B 2 through Ne 2 Notice the trends in bond order, bond energy and bond length 94

Section 10. 8 Molecular Orbital Theory: Electron Delocalization Learning Check • O 2 has been shown in experiments to be paramagnetic. Show MO theory is consistent with this observation where VSEPR and valence bond theory are not. 95

Section 10. 8 Molecular Orbital Theory: Electron Delocalization Period Two Heteronuclear Diatomic Molecules • We can apply MO theory to heteronuclear diatomic molecules • Note: – Oxygen is more electronegative than nitrogen − Atomic orbitals of oxygen −Are closer in energy to MO • Order of MO follows Oxygen 96

Section 10. 8 Molecular Orbital Theory: Electron Delocalization Period Two Heteronuclear Diatomic Molecules • We can apply MO theory to heteronuclear diatomic molecules • Flourine 1 s so lo in E it does not even make MO Hydrogen 1 s + Fluorine 2 p Make a single s bonding MO Fluorines other electrons remain localized on the fluorine and appear in the energy diagram as “non bonding MO” 97

Section 10. 8 Molecular Orbital Theory: Electron Delocalization Learning Check • USE MO theory to determine the bond order of NO. Is NO paramagnetic or diamagnetic? 98

Section 10. 8 Molecular Orbital Theory: Electron Delocalization Polyatomic Molecules • Molecular orbital theory is particularly useful in visualizing resonance structures. • The structure of ozone is represented as two equivalent bonds delocalized over the three oxygen atoms. 99

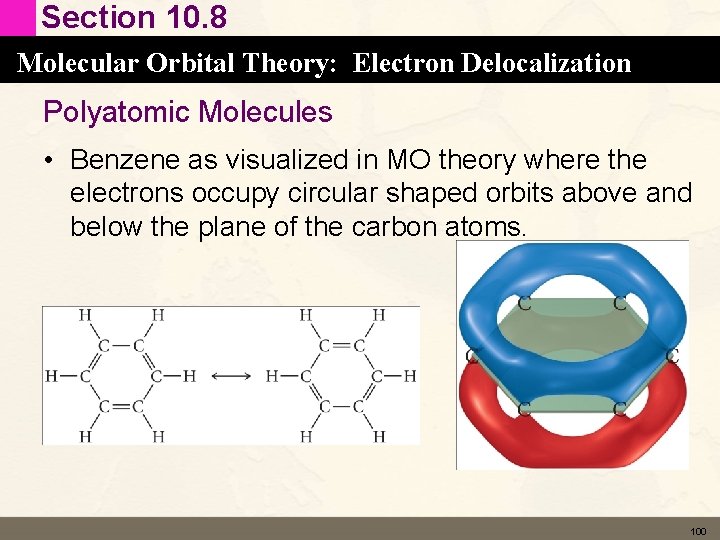
Section 10. 8 Molecular Orbital Theory: Electron Delocalization Polyatomic Molecules • Benzene as visualized in MO theory where the electrons occupy circular shaped orbits above and below the plane of the carbon atoms. 100