Chapter 10 Binary Trees Data Structures Using Java

Chapter 10 Binary Trees Data Structures Using Java 1

Chapter Objectives • • Learn about binary trees Explore various binary tree traversal algorithms Learn how to organize data in a binary search tree Discover how to insert and delete items in a binary search tree • Explore nonrecursive binary tree traversal algorithms • Learn about AVL (height-balanced) trees Data Structures Using Java 2

Binary Trees • Definition: A binary tree, T, is either empty or such that: – T has a special node called the root node; – T has two sets of nodes, LT and RT, called the left subtree and right subtree of T, respectively; – LT and RT are binary trees Data Structures Using Java 3

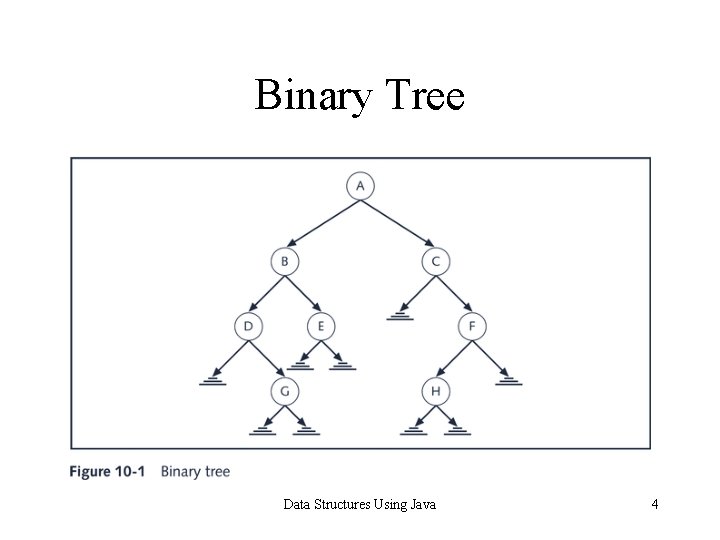
Binary Tree Data Structures Using Java 4

Binary Tree with One Node The root node of the binary tree = A LA = empty RA = empty Data Structures Using Java 5

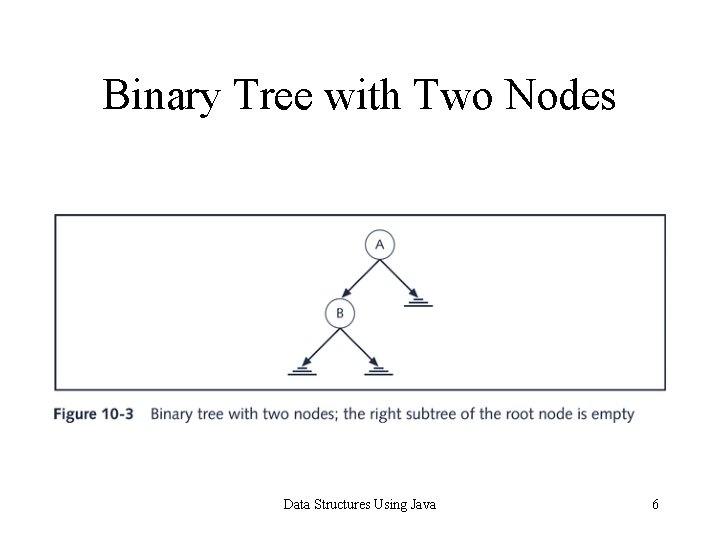
Binary Tree with Two Nodes Data Structures Using Java 6

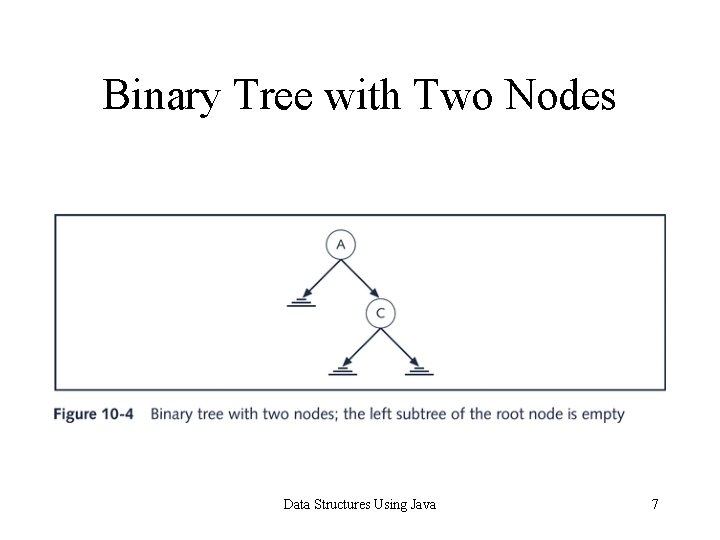
Binary Tree with Two Nodes Data Structures Using Java 7

Various Binary Trees with Three Nodes Data Structures Using Java 8

Binary Trees Following class defines the node of a binary tree: protected class Binary. Tree. Node { Data. Element info; Binary. Tree. Node llink; Binary. Tree. Node rlink; } Data Structures Using Java 9

Nodes • For each node: – Data is stored in info – The reference to the left child is stored in llink – The reference to the right child is stored in rlink Data Structures Using Java 10

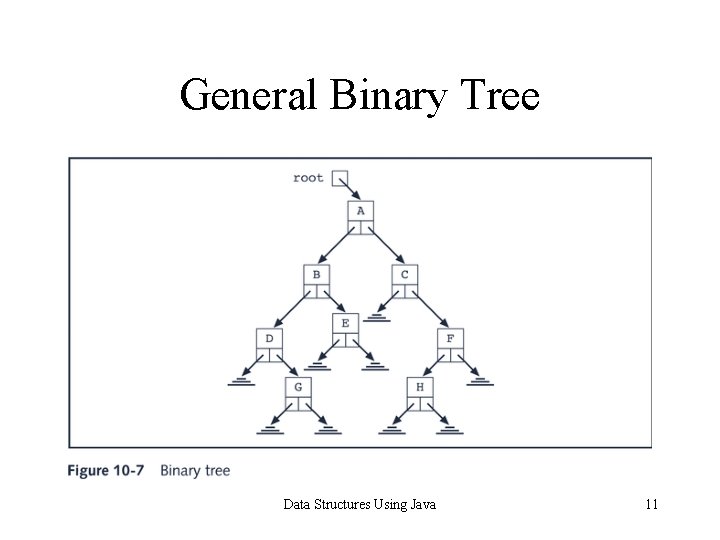
General Binary Tree Data Structures Using Java 11

Binary Tree Definitions • Leaf: node that has no left and right children • Parent: node with at least one child node • Level of a node: number of branches on the path from root to node • Height of a binary tree: number of nodes no the longest path from root to node Data Structures Using Java 12

Height of a Binary Tree Recursive algorithm to find height of binary tree: (height(p) denotes height of binary tree with root p): if(p is NULL) height(p) = 0 else height(p) = 1 + max(height(p. llink), height(p. rlink)) Data Structures Using Java 13

Height of a Binary Tree Method to implement above algorithm: private int height(Binary. Tree. Node p) { if(p == NULL) return 0; else return 1 + max(height(p. llink), height(p. rlink)); } Data Structures Using Java 14

Copy Tree • Useful operation on binary trees is to make identical copy of binary tree • Method copy useful in implementing copy constructor and method copy. Tree Data Structures Using Java 15

Method copy Binary. Tree. Node copy(Binary. Tree. Node other. Tree. Root) { Binary. Tree. Node temp; if(other. Tree. Root == null) temp = null; else { temp = new Binary. Tree. Node(); temp. info = other. Tree. Root. info. get. Copy(); temp. llink = copy(other. Tree. Root. llink); temp. rlink = copy(other. Tree. Root. rlink); } return temp; }//end copy Data Structures Using Java 16

Method copy. Tree public void copy. Tree(Binary. Tree other. Tree) { if(this != other. Tree) //avoid self-copy { root = null; if(other. Tree. root != null) //other. Tree is //nonempty root = copy(other. Tree. root); } } Data Structures Using Java 17

Binary Tree Traversal • Must start with the root, then – Visit the node first or – Visit the subtrees first • Three different traversals – Inorder – Preorder – Postorder Data Structures Using Java 18

Traversals • Inorder – Traverse the left subtree – Visit the node – Traverse the right subtree • Preorder – Visit the node – Traverse the left subtree – Traverse the right subtree Data Structures Using Java 19

Traversals • Postorder – Traverse the left subtree – Traverse the right subtree – Visit the node Data Structures Using Java 20

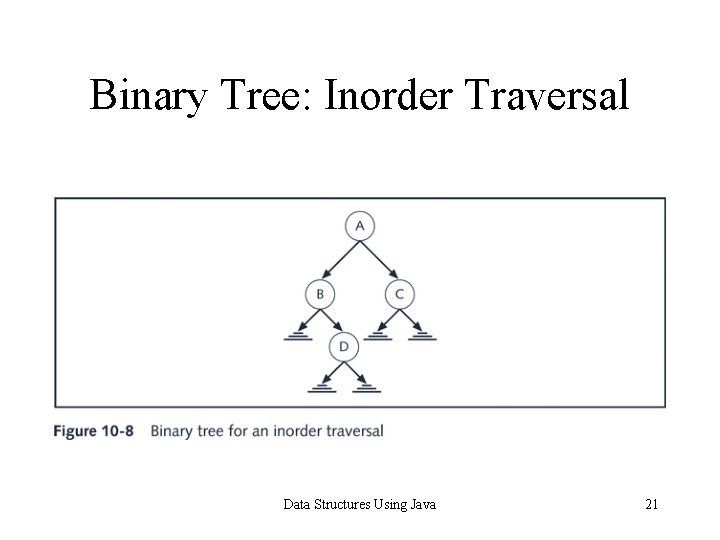
Binary Tree: Inorder Traversal Data Structures Using Java 21

Binary Tree: Inorder Traversal private void inorder(Binary. Tree. Node p) { if(p != NULL) { inorder(p. llink); System. out. println(p. info + “ “); inorder(p. rlink); } } Data Structures Using Java 22

Binary Tree: Preorder Traversal private void preorder(Binary. Tree. Node p) { if(p != NULL) { System. out. println(p. info + “ “); preorder(p. llink); preorder(p. rlink); } } Data Structures Using Java 23

Binary Tree: Postorder Traversal private void postorder(Binary. Tree. Node p) { if(p != NULL) { postorder(p. llink); postorder(p. rlink); System. out. println(p. info + “ “); } } Data Structures Using Java 24

Implementing Binary Trees: class Binary. Tree methods • • • is. Empty inorder. Traversal preorder. Traversal postorder. Traversal tree. Height tree. Node. Count tree. Leaves. Count destroy. Tree copy. Tree • • Copy Inorder Preorder postorder Height Max node. Count leaves. Count Data Structures Using Java 25

Binary Search Trees • Data in each node – Larger than the data in its left child – Smaller than the data in its right child • A binary search tree, t, is either empty or: – T has a special node called the root node – T has two sets of nodes, LT and RT, called the left subtree and right subtree of T, respectively – Key in root node larger than every key in left subtree and smaller than every key in right subtree – LT and RT are binary search trees Data Structures Using Java 26

Binary Search Trees Data Structures Using Java 27

Operations Performed on Binary Search Trees • • Determine whether the binary search tree is empty Search the binary search tree for a particular item Insert an item in the binary search tree Delete an item from the binary search tree Data Structures Using Java 28

Operations Performed on Binary Search Trees • • • Find the height of the binary search tree Find the number of nodes in the binary search tree Find the number of leaves in the binary search tree Traverse the binary search tree Copy the binary search tree Data Structures Using Java 29

Binary Search Tree: Analysis Data Structures Using Java 30

Binary Search Tree: Analysis • Theorem: Let T be a binary search tree with n nodes, where n > 0. The average number of nodes visited in a search of T is approximately 1. 39 log 2 n • Number of comparisons required to determine whether x is in T is one more than the number of comparisons required to insert x in T • Number of comparisons required to insert x in T same as the number of comparisons made in unsuccessful search, reflecting that x is not in T Data Structures Using Java 31

Binary Search Tree: Analysis It follows that: It is also known that: Solving Equations (10 -1) and (10 -2) Data Structures Using Java 32

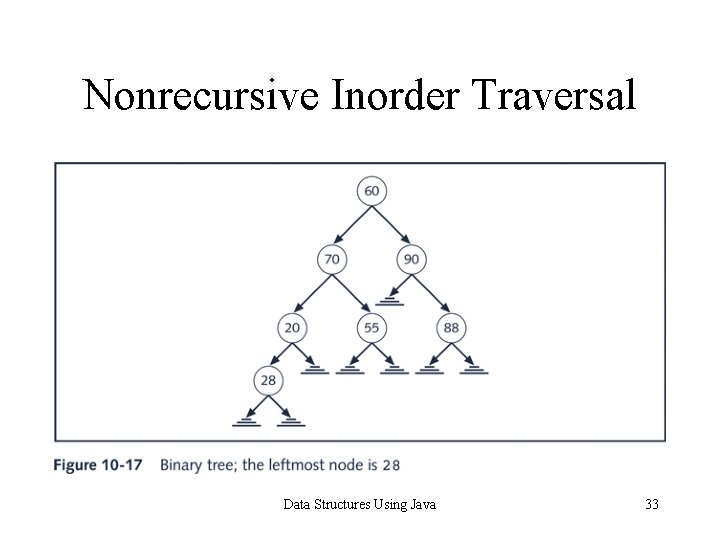
Nonrecursive Inorder Traversal Data Structures Using Java 33

Nonrecursive Inorder Traversal: General Algorithm 1. 2. current = root; //start traversing the binary tree at // the root node while(current is not NULL or stack is nonempty) if(current is not NULL) { push current onto stack; current = current. llink; } else { pop stack into current; visit current; //visit the node current = current. rlink; //move to the right child } Data Structures Using Java 34

Nonrecursive Preorder Traversal General Algorithm 1. current = root; //start the traversal at the root node 2. while(current is not NULL or stack is nonempty) if(current is not NULL) { visit current; push current onto stack; current = current. llink; } else { pop stack into current; current = current. rlink; //prepare to visit //the right subtree } Data Structures Using Java 35

Nonrecursive Postorder Traversal 1. 2. 3. 4. current = root; //start traversal at root node v = 0; if(current is NULL) the binary tree is empty if(current is not NULL) a. push current into stack; b. push 1 onto stack; c. current = current. llink; d. while(stack is not empty) if(current is not NULL and v is 0) { push current and 1 onto stack; current = current. llink; } Data Structures Using Java 36

Nonrecursive Postorder Traversal (Continued) else { pop stack into current and v; if(v == 1) { push current and 2 onto stack; current = current. rlink; v = 0; } else visit current; } Data Structures Using Java 37

AVL (Height-Balanced Trees) • A perfectly balanced binary tree is a binary tree such that: – The height of the left and right subtrees of the root are equal – The left and right subtrees of the root are perfectly balanced binary trees Data Structures Using Java 38

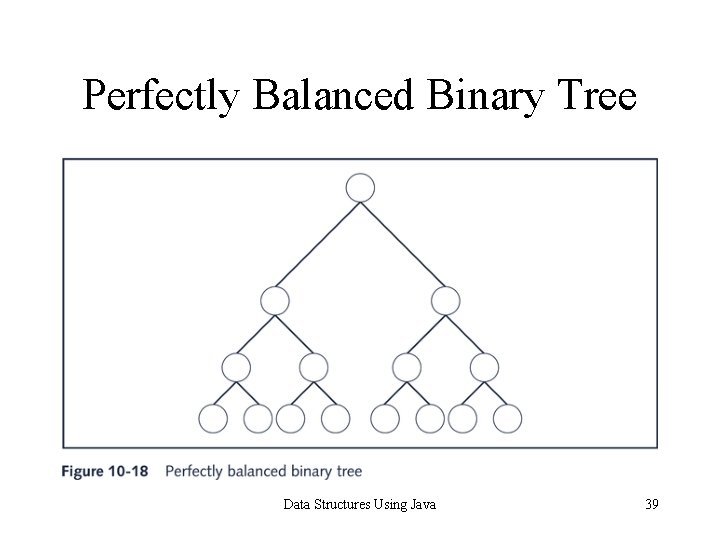
Perfectly Balanced Binary Tree Data Structures Using Java 39

AVL (Height-Balanced Trees) • An AVL tree (or height-balanced tree) is a binary search tree such that: – The height of the left and right subtrees of the root differ by at most 1 – The left and right subtrees of the root are AVL trees Data Structures Using Java 40

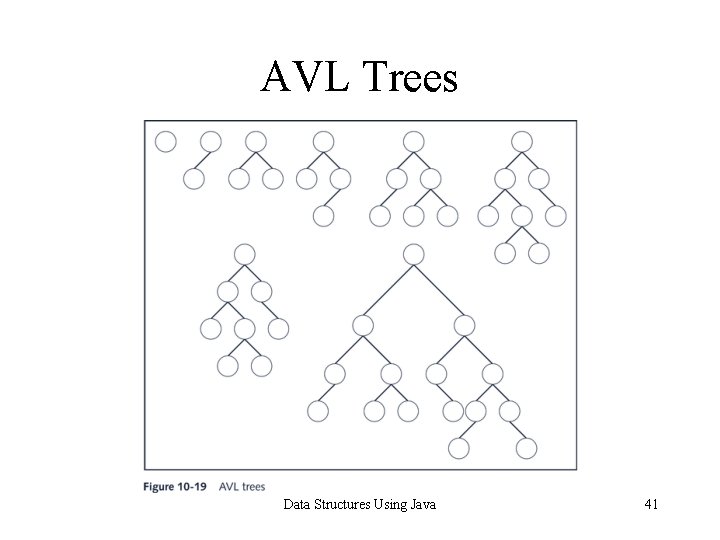
AVL Trees Data Structures Using Java 41

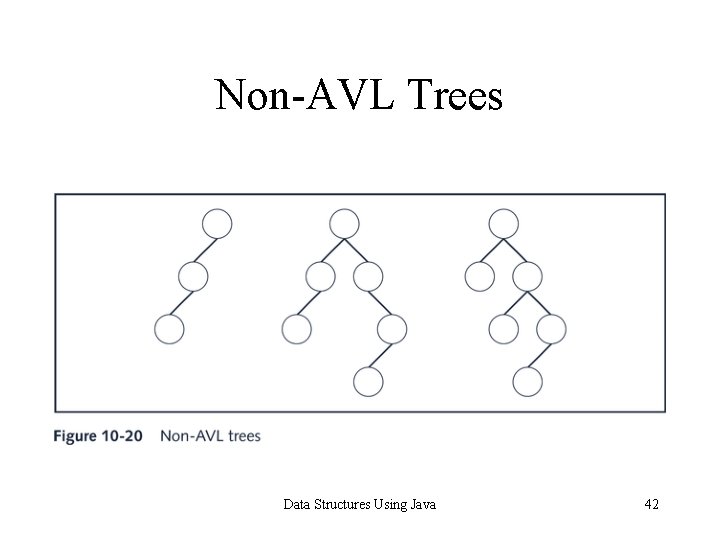
Non-AVL Trees Data Structures Using Java 42

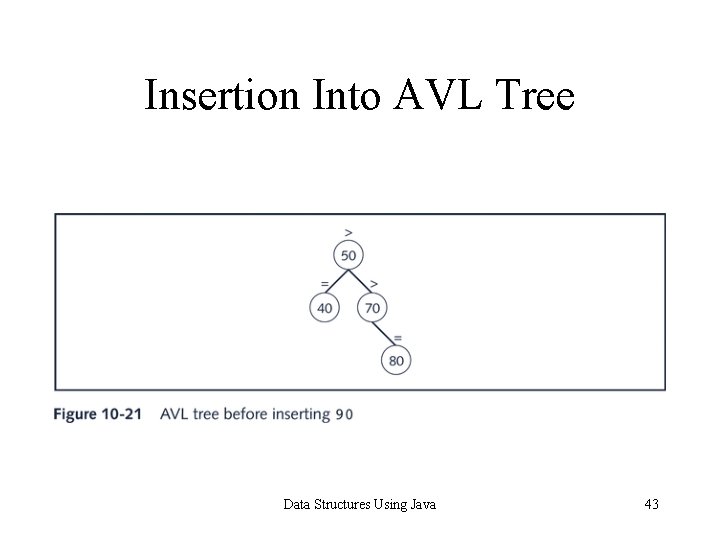
Insertion Into AVL Tree Data Structures Using Java 43

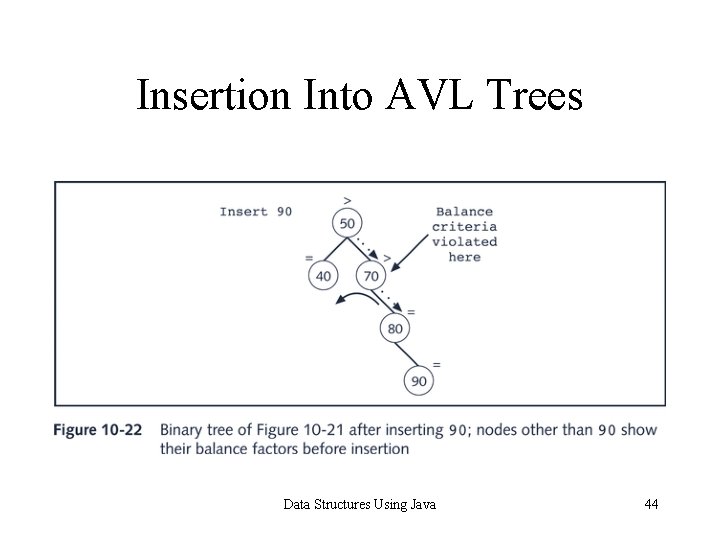
Insertion Into AVL Trees Data Structures Using Java 44

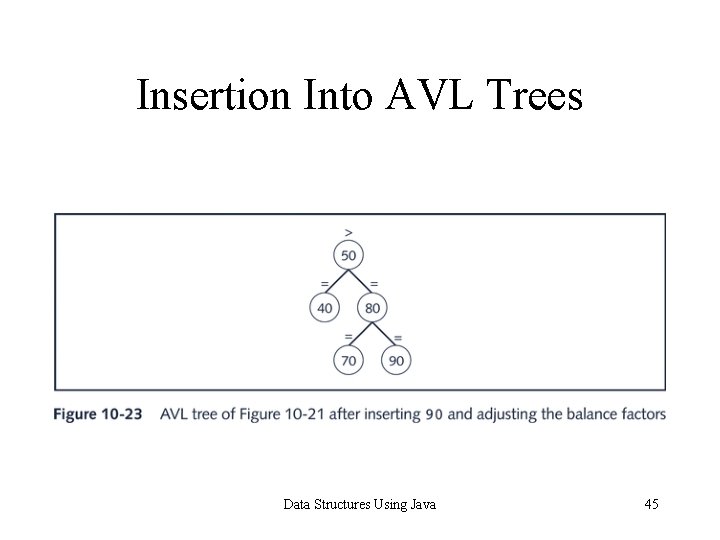
Insertion Into AVL Trees Data Structures Using Java 45

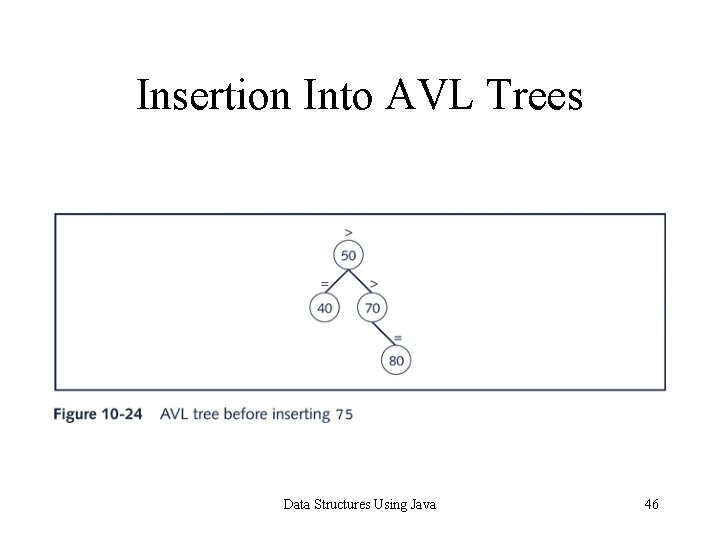
Insertion Into AVL Trees Data Structures Using Java 46

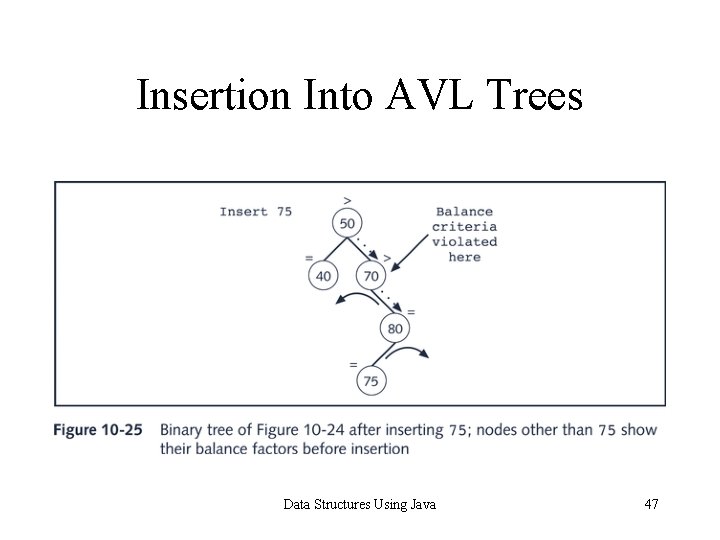
Insertion Into AVL Trees Data Structures Using Java 47

AVL Tree Rotations • Reconstruction procedure: rotating tree • left rotation and right rotation • Suppose that the rotation occurs at node x • Left rotation: certain nodes from the right subtree of x move to its left subtree; the root of the right subtree of x becomes the new root of the reconstructed subtree • Right rotation at x: certain nodes from the left subtree of x move to its right subtree; the root of the left subtree of x becomes the new root of the reconstructed subtree Data Structures Using Java 48

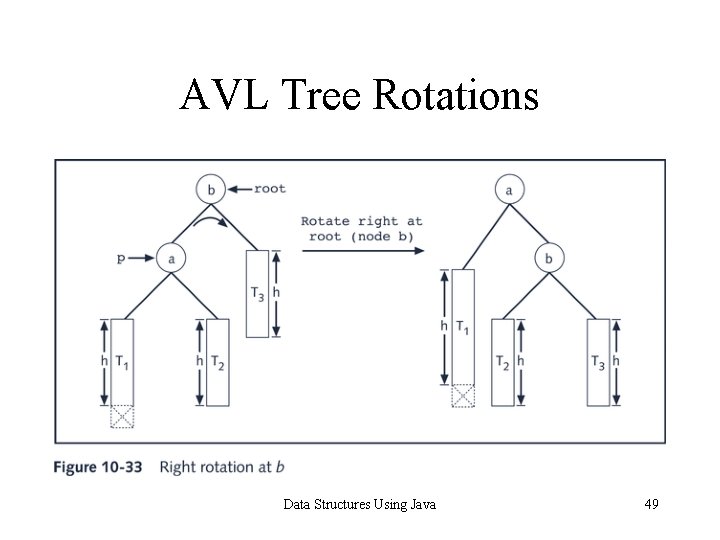
AVL Tree Rotations Data Structures Using Java 49

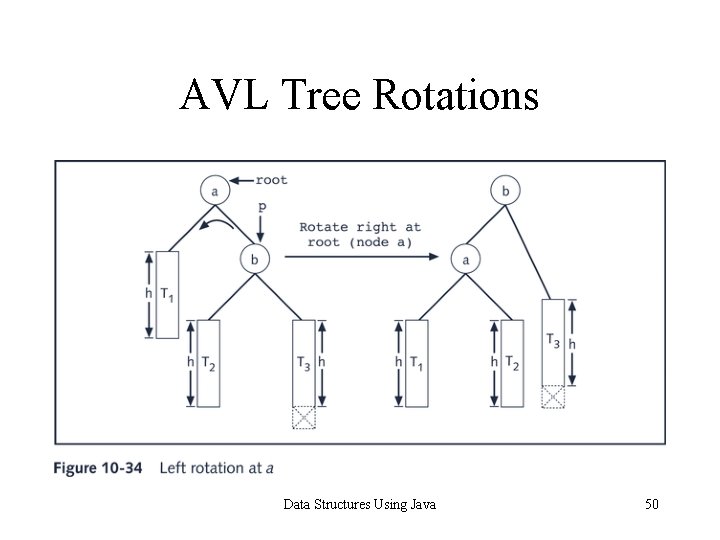
AVL Tree Rotations Data Structures Using Java 50

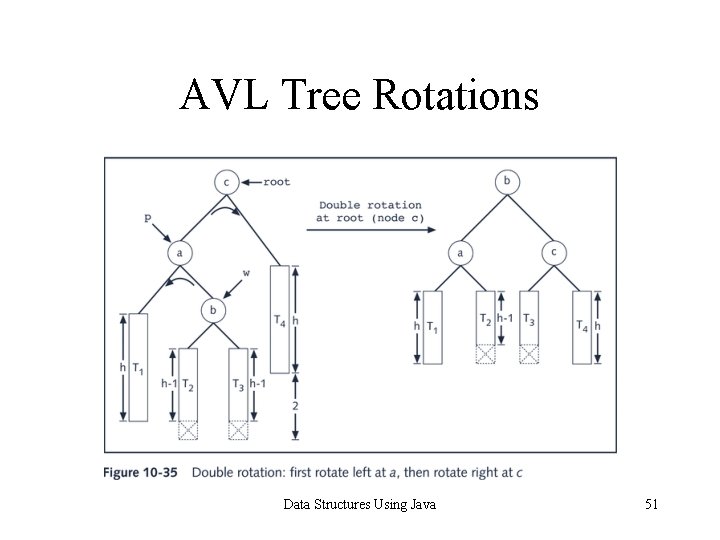
AVL Tree Rotations Data Structures Using Java 51

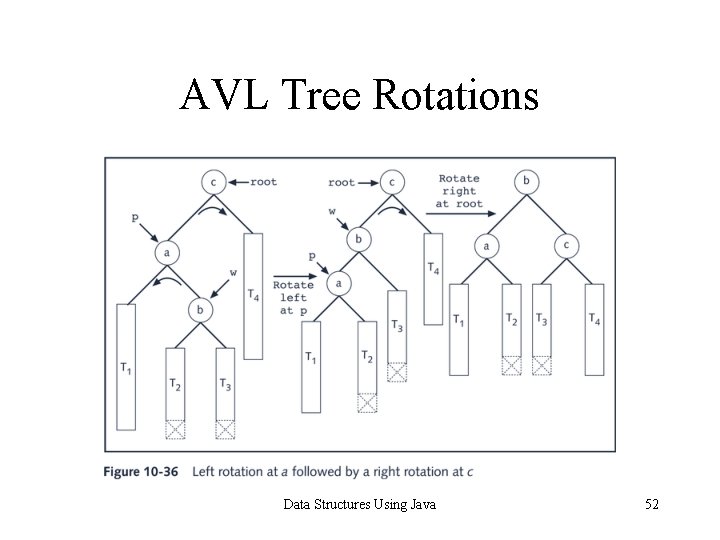
AVL Tree Rotations Data Structures Using Java 52

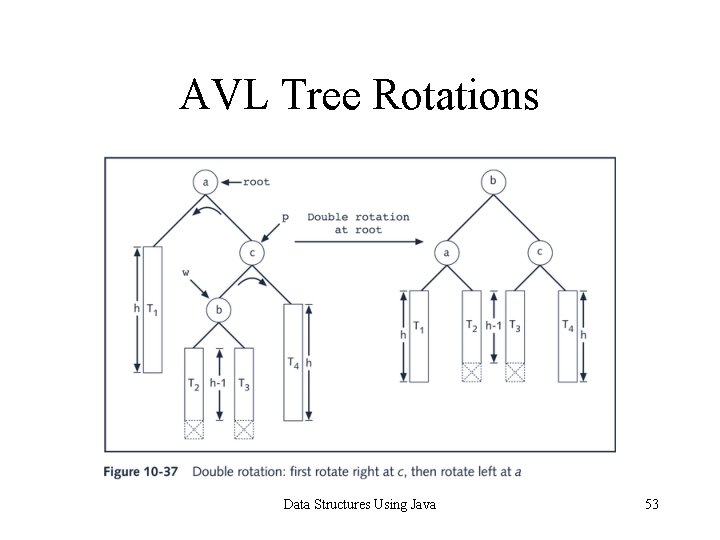
AVL Tree Rotations Data Structures Using Java 53

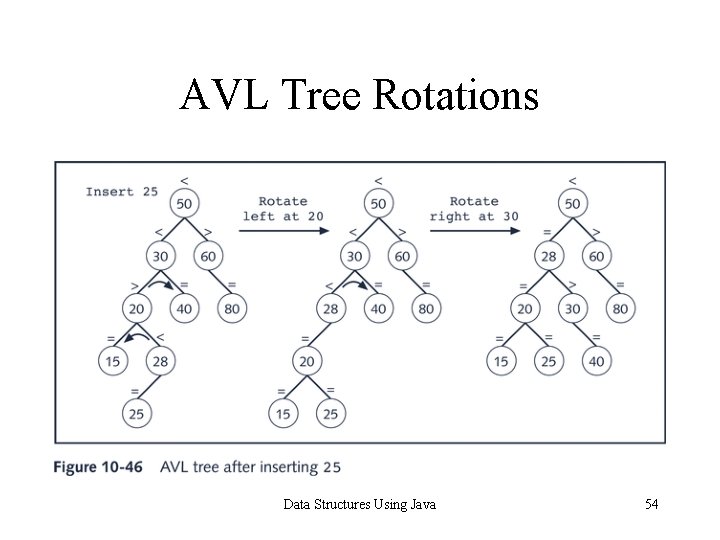
AVL Tree Rotations Data Structures Using Java 54

Deletion From AVL Trees • Case 1: the node to be deleted is a leaf • Case 2: the node to be deleted has no right child, that is, its right subtree is empty • Case 3: the node to be deleted has no left child, that is, its left subtree is empty • Case 4: the node to be deleted has a left child and a right child Data Structures Using Java 55

Analysis: AVL Trees Consider all the possible AVL trees of height h. Let Th be an AVL tree of height h such that Th has the fewest number of nodes. Let Thl denote the left subtree of Th and Thr denote the right subtree of Th. Then: where | Th | denotes the number of nodes in Th. Data Structures Using Java 56

Analysis: AVL Trees Suppose that Thl is of height h – 1 and Thr is of height h – 2. Thl is an AVL tree of height h – 1 such that Thl has the fewest number of nodes among all AVL trees of height h – 1. Thr is an AVL tree of height h – 2 that has the fewest number of nodes among all AVL trees of height h – 2. Thl is of the form Th -1 and Thr is of the form Th -2. Hence: Data Structures Using Java 57

Analysis: AVL Trees Let Fh+2 = |Th | + 1. Then: Called a Fibonacci sequence; solution to Fh is given by: Hence From this it can be concluded that Data Structures Using Java 58

Programming Example: Video Store (Revisited) • In Chapter 4, we designed a program to help a video store automate its video rental process. • That program used an (unordered) linked list to keep track of the video inventory in the store. • Because the search algorithm on a linked list is sequential and the list is fairly large, the search could be time consuming. • If the binary tree is nicely constructed (that is, it is not linear), then the search algorithm can be improved considerably. • In general, item insertion and deletion in a binary search tree is faster than in a linked list. • We will redesign the video store program so that the video inventory can be maintained in a binary tree. Data Structures Using Java 59

Chapter Summary • • • Binary trees Binary search trees Recursive traversal algorithms Nonrecursive traversal algorithms AVL trees Data Structures Using Java 60